Доклады Российской академии наук. Физика, технические науки, 2020, T. 494, № 1, стр. 35-41

Осциллирующее воздействие может привести к появлению в отклике системы не только осцилляций, но и медленной составляющей. “Медленность” означает, что параметры системы заметно изменяются на временах, больших по сравнению с периодом колебаний. Наряду с такими эффектами, как радиационное давление света и звука, известна сила Гапонова–Миллера, приводящая к дрейфу электронов в неоднородном поле электромагнитных микроволн. За “лазерный пинцет” – манипулятор микрочастиц с помощью такой силы, создаваемой оптическим излучением, недавно присуждена Нобелевская премия.

В жидкостях и газах радиационные силы вызывают появление течений среды. Потоки могут возбуждаться не только звуком, но и поверхностными волнами (гравитационными, капиллярными) и, вообще говоря, волнами любой другой природы. Твердые тела течь не могут, и поэтому радиационные напряжения вызывают в них лишь медленно изменяющиеся деформации.

Вибрационно-индуцированные явления широко известны в механике. Так, при вертикальных колебаниях подвеса маятника устойчивой может стать верхняя точка траектории, соответствующая отклонению вертикально вверх [1]. Такую систему называют маятником Капицы [2]. Другой пример: вибрации наклонной плоскости могут передвигать лежащие грузы не вниз, а вверх. Сформировался раздел – вибрационная механика [3]. Здесь изучаются важные для техники явления, например: вибрационная транспортировка сыпучих материалов, вибрационное погружение свай, сепарация частиц по размерам и другие.

Исторически первые работы в этом направлении связаны с акустическими радиационными силами и акустическими течениями. По акустическим течениям опубликованы тысячи работ, выполненных со времен Фарадея, Рэлея, Ланжевена, Бриллюена и до наших дней [4]. К сожалению, многие теоретические работы содержат неточности либо противоречат друг другу. Обсуждение этих проблем начато в работах [5, 6]. Обилие статей и нечеткость в формулировках способствовали появлению интенсивного “информационного шума” в этой области. Получилось так, что выделить из “шумового фона” полезную информацию без ее существенного искажения сегодня трудно, особенно начинающим исследователям. Общепринятые неточности могут мешать правильной интерпретации новых экспериментальных результатов, ориентированных на технические и особенно на медицинские приложения.

В этом сообщении сделана попытка “развеять” одно из заблуждений. Оно состоит в следующем. Считается, что вдали от препятствий существуют “быстрые” и “медленные” акустические течения. Медленные потоки типа течения Эккарта [7] возникают только в акустических полях малой интенсивности. Быстрые потоки, требующие учета гидродинамической нелинейности, возникают только в очень интенсивных акустических полях. Такая точка зрения, видимо, неточна. Более правильные выводы содержатся в книге [8] и цитированных в ней работах, однако сейчас стало ясно, что нужны более понятные объяснения.

В классических учебниках по гидродинамике указано (см., например, [9]), что приближение несжимаемой жидкости применимо к течениям со скоростями, гораздо меньшими скорости звука $\left( {\left| {{{U}_{i}}} \right| \ll {{c}_{0}}} \right)$. Такие течения вязкой жидкости описываются уравнениями [9]

Здесь F_i – компоненты вектора силы, приводящей жидкость в движение, P – гидродинамическое давление, $\nu $ – кинематическая вязкость, ${{\rho }_{0}}$ – постоянная плотность среды. В наших задачах F_i – это радиационная сила, создаваемая акустической волной. Для строгости к первому критерию $\left| {{{U}_{i}}} \right| \ll {{c}_{0}}$ применимости уравнений (1) следует добавить еще одно условие [9]: $\frac{L}{T} \ll {{c}_{0}}$, где $L$ – характерный масштаб течения, $T$ – характерное время его изменения. Правда, в учебниках не обсуждается особый случай – колебательные системы типа резонатора Гельмгольца; их размер меньше длины волны на резонансной частоте и колебательная скорость мала по сравнению с ${{c}_{0}}$, но сжимаемость учитывать необходимо. Очевидно, что для акустических течений такой особой ситуации нет, и оба неравенства $\left| {{{U}_{i}}} \right| \ll {{c}_{0}}$, $\frac{L}{T} \ll {{c}_{0}}$ “с запасом” выполнены. Типичные скорости потока не превышают нескольких м/с, характерные масштабы изменения потока – это сантиметры или метры, характерные времена – секунды.

Стационарное $\left( {\frac{{\partial {{U}_{i}}}}{{\partial t}} = 0} \right)$ и линейное $\left( {{{U}_{k}}\frac{{\partial {{U}_{i}}}}{{\partial {{x}_{k}}}} = 0} \right)$ решение уравнений (1) для цилиндрически-симметричного течения найдено Эккартом [7]. В его постановке в трубе с круглым поперечным сечением радиуса ${{r}_{0}}$ распространялся соосный недифрагирующий ультразвуковой пучок радиуса ${{r}_{1}} < {{r}_{0}}$. Радиационная сила возникала из-за поглощения волны, в результате которого среде передавалась часть переносимого волной импульса. Точное решение нестационарной задачи, в которой скорость течения зависит от времени после включения источника звука $\left( {\frac{{\partial {{U}_{i}}}}{{\partial t}} \ne 0} \right)$, получено в работе [10]. Более детально динамика установления течения Эккарта описана в работе [11]. Именно на результатах работ [7, 10] (см. также [8]) будут основаны дальнейшие рассуждения.

Имея точные линейные решения, можно определить область их применимости, оценив число Рейнольдса для течения:

Известно, что линейное решение справедливо, если во всех точках пространства и в любой момент времени $\operatorname{Re} \ll 1$. Критерием перехода к нелинейному режиму можно считать условие Re = 1, когда величины линейного и нелинейного членов в отношении (2) сравниваются. Если где-то число Рейнольдса имеет порядок единицы, требуется учет отброшенного нелинейного члена в уравнении движения (1). При $\operatorname{Re} \gg 1$ структура течения и его скорость уже принципиально не описываются линейным решением.

Для реализации описанного подхода и проведения оценок приведем необходимые формулы. Эккарт решил простую математическую задачу

Здесь $K = \frac{{dP}}{{dr}} = {\text{const}}$; H – единичная функция Хевисайда; ${{F}_{0}}$ – значение радиационной силы на оси пучка. Это решение для скорости акустического течения имеет вид [7]

Стационарная скорость течения (4) достигает максимума на оси пучка (при r = 0) и равна

Скорость (5) зависит от отношения радиусов пучка и трубы. Она обращается в ноль, когда пучок полностью заполняет трубу (r₁ = r₀), а также при нулевом радиусе пучка. Максимум достигается при ${{r}_{1}} \approx 0.45{{r}_{0}}$ и равен примерно 0.04$\frac{{{{F}_{0}}r_{0}^{2}}}{\nu }$.

Чтобы провести численные оценки скорости и гидродинамического числа Рейнольдса для течения Эккарта, нужно конкретизировать выражение для радиационной силы F₀. В этом есть еще одна проблема, потому что известные обзоры и монографии содержат разные формулы. Их сравнительный анализ нужно провести в отдельной работе. Пока же воспользуемся (без обсуждения) усредненным выражением для тензора плотности потока импульса, точнее, той его частью $\Pi _{{ik}}^{{RAD}}$, которая содержит только главные (квадратичные) комбинации параметров акустического поля. Сила вычисляется как дивергенция от него [9]:

Здесь $p{\kern 1pt} '$ – акустическое давление, ${{u}_{i}}$ – колебательная скорость в акустической волне, $\beta $ – параметр физической нелинейности, равный $(\gamma - 1){\text{/}}2$ для адиабатических газов. Заметим, что в формуле (6) присутствует нелинейный коэффициент, хотя никакой волны мы пока не рассматривали. Он появился из-за того, что в квадратично-нелинейном выражении для тензора плотности потока импульса (6) учтена не только линейная, но и нелинейная сжимаемость среды.

Для задачи Эккарта, когда волна считается плоской, бегущей вдоль оси x цилиндрической системы координат, выражение (6) упрощается:

Здесь $\varepsilon = \beta + 1$ – полный нелинейный акустический параметр [8], включающий физическую и геометрическую нелинейности.

Полезно преобразовать (7) к форме, пригодной одновременно как для линейной, так и для нелинейной акустической волны. Известно, что такая плоская волна описывается уравнением Бюргерса [8]:

Здесь $\tau = t - \frac{x}{{{{c}_{0}}}}$ – время в бегущей со скоростью звука системе координат, b – диссипативный коэффициент, включающий сдвиговую, объемную вязкости и теплопроводность среды [8]. Умножая все члены уравнения (8) на $p{\kern 1pt} '$ и усредняя результат по периоду колебаний, получим соотношение

Первые два члена правой части равны нулю, как средние значения производных по времени от периодических функций. В результате из (9) получается полезная формула

с учетом которой выражение (7) для радиационной силы принимает вид

Если течение вызывается линейной бегущей волной, затухающей из-за вязкости и теплопроводности, т.е.

из формулы (11) следует

Видно, что радиационная сила, вызываемая слабой (линейной) волной, пропорциональна нелинейному параметру ε и квадрату амплитуды волны.

Если волна – пилообразная с конечной шириной фронта, то один ее период хорошо описывается (при малых обратных акустических числах Рейнольдса Γ – числах Гольдберга) решением Хохлова [12]:

Здесь $Z$ – расстояние x, поделенное на характерную нелинейную длину ${{L}_{{NL}}}$ – длину образования разрыва. Число $\Gamma = \frac{{{{L}_{{NL}}}}}{{{{L}_{{DISS}}}}}$ – отношение характерных “нелинейной” и “диссипативной” длин. Эти длины даются выражениями

Как показали численные расчеты, нелинейные акустические эффекты заметно выражены (ударный фронт узок по сравнению с длиной волны, гармоник образуется много, нелинейное поглощение преобладает над линейным) в тех случаях, когда Γ < 0.1. Это же неравенство есть условие применимости решения (14).

Подставляя (14) в (11), найдем радиационную силу, вызванную нелинейным поглощением пилообразной волны:

Нелинейная радиационная сила пропорциональна квадрату нелинейного параметра и кубу амплитуды волны. Поскольку решение (14) является асимптотикой формы профиля исходного гармонического сигнала, причем с хорошей точностью при $Z \geqslant 3$, положим в формулах (13) и (16) расстояния равными $x = 0$ (в формуле (13)) и Z = 3 (в формуле (16)), после чего сравним полученные выражения: $\frac{{F_{0}^{{NL}}}}{{F_{0}^{{LIN}}}} \approx \frac{{{{\pi }^{2}}}}{{96\Gamma }}$. Таким образом, при Γ ~ 0.1 линейная и нелинейная волна создают радиационные силы одного порядка величины. При меньших значениях $\Gamma $ “нелинейная сила” может заметно превосходить “линейную”.

Оценим скорость эккартовского течения на оси, пользуясь формулами (5) и (13):

Здесь I – интенсивность волны. Полагая радиус кюветы r₀ = 5 см, параметры среды (воды): $\nu $ = 10^–2 Пз, нелинейность ε = 4, коэффициент поглощения ${{\alpha }^{{ - 1}}} = 0.5$ × 10² см (он соответствует ультразвуковым частотам порядка 5 МГц), оценим U_max ~ ${{10}^{{ - 4}}}I$. Отсюда следует, что при интенсивностях волны порядка 10^–3 Вт/см² скорость течения – порядка 1 см/с. Однако уже для значений интенсивности в десятые доли Вт/см² скорость может увеличиться до 1 м/с.

Оценим теперь, способна ли слабая акустическая волна привести к появлению течений с выраженной гидродинамической нелинейностью. Подставляя (3) в (2), найдем выражение для числа Рейнольдса (14):

Здесь для краткости обозначено $X = \frac{{{{r}^{2}}}}{{r_{0}^{2}}},$ $D = \frac{{r_{1}^{2}}}{{r_{0}^{2}}}$. Из формулы (18) следуют очевидные предельные переходы. Число Рейнольдса равно нулю на стенке трубы (X = 1), и на оси пучка (X = 0), а также при $D = 1$, когда пучок полностью заполняет трубу.

Элементарный расчет показывает, что число Рейнольдса (18) как функция двух переменных $X,\,D$ имеет абсолютный максимум, примерно равный

Для линейной гармонической волны (12), (13) оценочная формула (19) примет вид

Для численных значений констант, использованных выше при оценках скорости течения (17), найдем ${{\operatorname{Re} }_{{\max }}} = 3 \times {{10}^{{ - 4}}}I$. Таким образом, переход к нелинейному течению в рассмотренной кювете происходит при сравнительно небольших интенсивностях порядка 0.3 мВт/см². Покажем, что волна при этом заведомо остается линейной. Для этого оценим обратное акустическое число Рейнольдса (14). Наглядная оценка получится, если исключить интенсивность волны из двух выражений (14) и (20). При этом

Для значений параметров, использованных ранее, ${{\operatorname{Re} }_{{\max }}} = 1$, а оценка обратного акустического числа Рейнольдса по формуле (21) дает Γ ~ 100. Как указывалось выше, при Γ > 1 акустическая нелинейность проявляется слабо.

Итак, линейная акустическая волна может вызвать гидродинамически нелинейное течение. Обратно, нелинейная пилообразная волна может вызвать линейное течение в трубках малого радиуса, заполненных жидкостью с большой сдвиговой вязкостью (см. (20)). Конечно, при больших интенсивностях звука акустически нелинейная волна должна формировать гидродинамически нелинейное течение, если объем среды достаточно велик.

Все сказанное относилось к стационарным во времени (установившимся) течениям. Обсудим теперь, когда и как проявляются нелинейные явления в процессе установления. Нестационарное течение эккартовского типа рассчитано в работе [10] (см. также [8]). Решение получено в виде ряда, который формально запишем так:

Здесь ${{C}_{n}},$ ${{\Phi }_{n}}$ – функции, конкретный вид которых для последующих оценок несущественен, ${{\mu }_{n}}$ – $n$-й корень функции Бесселя второго порядка,

Точная оценка требует численного суммирования ряда (22), однако правильные результаты можно получить из приближенного аналитического рассмотрения. Нетрудно проверить, что качественное описание процесса установления дается уже первым членом ряда (22) [8]. Это означает, что можно взять стационарную форму (4) для структуры течения, считая ее неизменной по сечению трубы, но со значениями скорости, растущими во времени по закону (23) (n = 1). Это позволяет сразу оценить характерное время установления:

Здесь ${{\mu }_{1}} \approx 5.14$ – первый корень функции Бесселя второго порядка. Из (24) следует, что в цилиндрической кювете с водой радиусом 5 см линейное течение устанавливается за времена порядка 100 с. Когда стенки трубы находятся очень далеко от оси, ${{r}_{0}} \to \infty $, время установления ${{t}_{{ST}}}$ также стремится к бесконечности. Это означает, что в больших объемах вязкость среды не может затормозить течение, скорость которого неограниченно нарастает со временем. Только нелинейные гидродинамические явления могут привести к формированию стационарного потока в неограниченной среде. О структуре нелинейного потока, механизмах ограничения и характерных значениях скорости сказано ниже.

Число Рейнольдса течения, очевидно, растет по тому же самому закону ${{f}_{1}}(t)$ (23). При достаточно больших значениях радиационной силы может возникнуть ситуация, когда на малых временах, в начале разгона течение будет линейным. Затем его скорость увеличится и произойдет переход в нелинейный режим течения. Для оценки момента времени, в который число Re_max достигнет критического значения ${{\operatorname{Re} }_{{\max }}} = 1$, разложим экспоненту ${{f}_{1}}(t)$ (23) в ряд с удержанием линейного по времени члена. Считая акустическую волну линейной, получим “нестационарный аналог” формулы (20):

В момент времени $t = {{t}_{{NL}}}$, когда число Re_max обратится в единицу, начинают действовать нелинейные эффекты, искажающие структуру эккартовского течения. Типичным проявлением в эксперименте является образование фронта течения и связанного с ним кольцевого вихря, наблюдавшегося и детально описанного Н.Г. Семеновой (см. [8]). Аналогичная структура, похожая на гриб, формируется при сильных наземных взрывах в атмосфере.

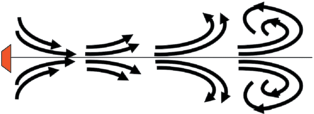
Процесс нелинейного искажения линий тока схематически показан на рис. 1 для четырех последовательных моментов времени. Источник звука находится на твердой (непроницаемой для потока) стенке x = 0, ось пучка совпадает с осью $x$. В момент t = 0 звук включается, и радиационная сила начинает разгонять течение. Когда поток ускорится и станет нелинейным, начнется образование выраженного фронта течения, который затем трансформируется в кольцевой вихрь. После прохождения фронта позади него течение быстро устанавливается.

Теория гидродинамически нелинейных акустических течений дана в книге [8]. Развитие нестационарной нелинейной теории изложено в работах [10, 13]. Тесная связь нелинейных течений с затопленными струями обсуждена в обзоре [15]. Хотя теория [13, 14] основана на сильных упрощениях, в ней содержатся формулы, позволяющие грубо оценить порядок величины скорости нелинейного потока. Установившаяся скорость течения на оси пучка в точке $x$ дается формулой

Подставляя в (26) выражения (13) и (16) для радиационной силы, вызванной, соответственно, линейным и нелинейным поглощением волны, найдем:

Видно, что нелинейность течения ограничивает его скорость значительно сильнее, чем вязкие потери на стенках. Скорость здесь увеличивается с ростом интенсивности как I^1/2, т.е. медленнее, чем в эккартовском течении, вызванном поглощением гармонической (~I) или пилообразной ($\sim {\kern 1pt} {{I}^{{3/2}}}$) волны. При интенсивностях звука порядка 1 Вт/см² скорость течения, вызванного пилообразной волной (вторая формула (27)), оказывается порядка 50 см/с. Скорость движения фронта течения примерно вдвое меньше.

В этом сообщении сделана попытка обратить внимание на одну из проблем, которые слабо или неточно отражены в обзорах и монографиях по нелинейной акустике, обсуждающих проблемы радиационных сил и акустических течений. Конечно, желательно иметь справочные таблицы, позволяющие для каждого конкретного эксперимента оценить скорость акустического течения и понять, насколько нелинейные явления в данном случае существенны. Накопление такого справочного материала требует компьютерных расчетов. Мы надеемся, что высказанные соображения помогут провести такие расчеты, а пока их нет – избежать появления дальнейших неточностей в публикациях на эту тему.