Доклады Российской академии наук. Физика, технические науки, 2020, T. 495, № 1, стр. 50-56
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ВБЛИЗИ ЖЕСТКИХ ЦИЛИНДРИЧЕСКИХ ВКЛЮЧЕНИЙ В УСЛОВИЯХ АНТИПЛОСКОГО СДВИГА
Член-корреспондент РАН Е. В. Ломакин 1, 2, *, С. А. Лурье 2, 3, Л. Н. Рабинский 2, Ю. О. Соляев 2, 3
1 Московский государственный университет
имени М.В. Ломоносова
Москва, Россия
2 Московский авиационный институт (национальный исследовательский университет)
Москва, Россия
3 Институт прикладной механики
Российской академии наук
Москва, Россия
* E-mail: lomakin@mech.math.msu.su
Поступила в редакцию 28.08.2020
После доработки 15.09.2020
Принята к публикации 16.09.2020
Аннотация
Представлены аналитические решения задач о концентрации напряжений вблизи цилиндрического включения с круглым и эллиптическим поперечным сечением в условиях антиплоского сдвига. Решения построены в рамках изотропной градиентной теории упругости в предположении высокой жесткости включений по сравнению с матрицей, что соответствует типичным характеристикам волокнистых композиционных материалов. Показано, что вблизи тонких включений, размеры сечения которых сопоставимы с характерным размером микроструктуры материала матрицы, может происходить снижение концентрации напряжений по сравнению со стандартными оценками, известными в теории упругости. Для круговых цилиндрических включений получены замкнутые решения, справедливые для материалов с малым объемным содержанием включений, которые могут быть использованы для прогноза прочности композитов при сдвиге вдоль армирующих волокон, а также для идентификации дополнительных параметров градиентной теории упругости.
ВВЕДЕНИЕ
Проблема прогноза свойств композиционных материалов на основе моделей микромеханики к настоящему времени не является до конца решенной, что связано со сложным характером напряженно-деформированного состояния, реализующимся на уровне микроструктуры неоднородных материалов. Вследствие этого, в большинстве инженерных приложений при оценке прочности композитов используются макромеханические критерии, формулируемые на уровне однородного анизотропного монослоя [1]. Тем не менее, использование моделей микромеханики является эффективным и вполне оправданным подходом при оценке упругих свойств композитов и, в первом приближении, при оценке их прочности, особенно при проведении проектировочных или предварительных расчетов [1, 2].
В настоящей работе рассматривается проблема оценки концентрации напряжений в волокнистых композитах с учетом влияния диаметра армирующих волокон. Классическое решение задачи о цилиндрическом включении не позволяет получать такие оценки, так как не содержит масштабных параметров [3]. Привлекаемая в данной работе градиентная теория упругости учитывает, что энергия деформаций материала в общем случае зависит не только от первых производных от перемещений (в форме тензора деформаций), но и от производных более высокого порядка [4, 5]. Вследствие этого в формулировке градиентной теории упругости возникают материальные константы (модули) разной размерности, а ее решения позволяют оценивать влияние масштабных эффектов [6–9].
В настоящей работе рассматривается задача о продольном сдвиге вдоль волокон, которая в формулировке градиентной теории упругости допускает построение замкнутых аналитических решений в наиболее простой форме в случае включений с круглым поперечным сечением. Кроме того, исследуется влияние эллиптичности поперечного сечения волокон. Такую форму (эллиптическую или овальную) имеют некоторые типы высокопрочных углеродных волокон [10]. Аналогичные решения в рамках моментной теории упругости (couple stress) рассматривались ранее в работе [11].
ЗАДАЧА АНТИПЛОСКОГО СДВИГА В ГРАДИЕНТНОЙ ТЕОРИИ УПРУГОСТИ
В общем случае уравнения равновесия градиентной теории упругости для линейно упругого тела в отсутствии объемных сил могут быть представлены в следующем виде [4]:
(1)
$\begin{gathered} \left( {\lambda + 2\mu } \right)(1 - l_{1}^{2}\Delta )\nabla \nabla \cdot {\mathbf{u}} - \mu (1 - l_{2}^{2}\Delta )\nabla \times \nabla \times {\mathbf{u}} = 0, \\ {\mathbf{x}} \in {\Omega ,} \\ \end{gathered} $Рассмотрим случай антиплоских деформаций, при которых перемещения точек среды реализуются в направлении, коллинеарном оси x3, и зависят только от координат x1 и x2. Таким образом, мы предполагаем, что вектор перемещений имеет вид ${\mathbf{u}} = {{\left\{ {0,0,w\left( {{{x}_{1}},{{x}_{2}}} \right)} \right\}}^{{\text{T}}}}$, а соответствующий вид уравнений равновесия для задач антиплоского сдвига может быть получен из (1) в следующей форме [12]:
где l = l2.Граничные условия в градиентной теории в общем случае записываются относительно расширенного набора кинематических и статических переменных [4, 7, 8]. Для рассматриваемой в настоящей работе градиентной упругости существенным является тот факт, что граничные условия вблизи контакта деформируемого материала с жестким недеформируемым телом могут быть определены заданием одновременно нулевых перемещений и нулевых нормальных производных от вектора перемещений [8]. Второе условие является неклассическим и позволяет описать эффекты образования зоны стесненных деформаций и межфазного (пограничного) слоя вблизи жестких включений. Такого рода эффекты, связанные с расширением и уточнением краевых условий, позволяют описывать влияние размера включений на упругие характеристики нанокомпозитов [6–8]. Аналогичные эффекты в градиентных моделях гидродинамики позволяют учесть влияние размера наполнителей на динамическую вязкость наножидкостей [13].
В рассматриваемых далее задачах мы предполагаем, что включение является абсолютно жестким по сравнению с материалом матрицы. Это предположение является вполне допустимым, так как в конструкционных композитах модули упругости матрицы и включений могут отличаться в 100–200 раз. Таким образом, контакт матрицы с жестким включением может быть описан граничными условиями следующего вида:
где $~\partial {\Omega }$ – это граница контакта включения и матрицы и ${{\partial }_{n}}$ – производная в направлении внешней нормали к этой границе.Еще два условия, необходимые для отыскания решения уравнения равновесия четвертого порядка (2), определяются требованиями заданного однородного поля деформаций на бесконечности.
ЗАДАЧА ОБ ИЗОЛИРОВАННОМ ЦИЛИНДРИЧЕСКОМ ВКЛЮЧЕНИИ
Рассматриваем задачу об антиплоском сдвиге в бесконечной упругой среде, содержащей единственное цилиндрическое включение c эллиптическим поперечным сечением с полуосями а и b (рис. 1). На бесконечности задано состояние однородного сдвига в плоскости YZ, которое предполагает следующий вид функции перемещений:
где γ/2 – величина заданных деформаций сдвига, и $r = \sqrt {{{x}^{2}} + {{y}^{2}}} ,\,\,\theta = {\text{arctg}}\,y{\text{/}}x$ – радиальная и окружная координаты.Вначале рассмотрим общее решение уравнений равновесия (2) для включения круглого поперечного сечения (а = b = r0). Это решение имеет вид
(5)
$w(\bar {r},\theta ) = \left( {{{C}_{1}}~\bar {r} + \frac{{{{C}_{2}}}}{{\bar {r}}} + {{C}_{3}}{{I}_{1}}\left( {\bar {r}} \right) + {{C}_{4}}{{K}_{1}}\left( {\bar {r}} \right)} \right)\sin \theta ,$В случае однородного поля деформаций на бесконечности (4) имеем ${{C}_{1}} = \gamma ~l$ и ${{C}_{3}} = 0$. Подстановка решения (5) в граничные условия (3) позволяет определить оставшиеся константы C2 и C4. Напряжения в антиплоской задаче можно определить на основе инвариантного по отношению к системе координат соотношения [12]:
Подставляя решение (5) в (6) и учитывая найденные значения констант, можно получить следующее решение для физических компонент тензора напряжений в цилиндрической системе координат:
(7)
$\begin{gathered} {{\sigma }_{{zr}}}(\bar {r},\theta ) = \\ = \mu ~\gamma \left( {1 + \frac{{\bar {r}_{0}^{2}{{K}_{2}}({{{\bar {r}}}_{0}}) - {{{\bar {r}}}^{2}}{{K}_{0}}(\bar {r}) - {{{\bar {r}}}^{2}}{{K}_{2}}(\bar {r})}}{{{{{\bar {r}}}^{2}}{{K}_{0}}({{{\bar {r}}}_{0}})}}} \right){\text{sin}}\theta , \\ \end{gathered} $(8)
${{\sigma }_{{z\theta }}}(\bar {r},\theta ) = \mu ~\gamma ~\frac{{~{{{\bar {r}}}^{2}}{{K}_{0}}({{{\bar {r}}}_{0}}) + 2~\bar {r}~{{K}_{1}}(\bar {r}) - \bar {r}_{0}^{2}{{K}_{2}}({{{\bar {r}}}_{0}})~}}{{{{{\bar {r}}}^{2}}{{K}_{0}}({{{\bar {r}}}_{0}})}}~{\text{cos}}\theta ,$Далее рассмотрим общий случай эллиптического поперечного сечения. Такую задачу удобно решать в цилиндрической-эллиптической системе координат, в которой условие для поля перемещений на бесконечности (4) приводится к виду
где ${{с}^{2}} = {{a}^{2}} - {{b}^{2}}~$ – половина фокусного расстояния, а связь декартовых и эллиптических координат определяется соотношениями $x = c{\text{ch}}~\xi {\text{cos}}\eta $, $y = c{\text{sh}}~\xi {\text{sin}}\eta $.Для построения решения в эллиптических координатах общее решение уравнений равновесия (2) должно быть представлено в виде ряда, в котором можно сразу учесть симметрию и $~2\pi $-периодичность решения, а также требование однородного поля деформаций на бесконечности:
(10)
$\begin{gathered} w(\xi ,\eta ) = \gamma ~c{\text{sh}}\xi \sin \eta + \mathop \sum \limits_{n = 1,3,5 \ldots }^\infty {{C}_{{1n}}}~{{{\text{e}}}^{{ - n~\xi }}}{\text{sin(}}\eta ,q) + \\ + \mathop \sum \limits_{m = 1,3,5 \ldots }^\infty {{C}_{{2m}}}~K{{o}_{m}}(\xi ,q)~s{{e}_{m}}(\eta ,q), \\ \end{gathered} $Следует отметить, что в решении (10) слагаемые, связанные с коэффициентами C1n и C2m, удовлетворяют уравнениям Лапласа и Гельмгольца, соответственно, что соответствует общей теореме представления решения для градиентной теории упругости [14]. Однако, важным здесь является тот факт, что классическое решение может быть получено с использованием единственного слагаемого ${{C}_{{11}}}~{{{\text{e}}}^{{ - ~\xi }}}{\text{sin}}\eta $, удовлетворяющего уравнению Лапласа, в то время как в рамках градиентной теории возникает необходимость рассмотрения полного разложения, как для градиентной, так и для классической частей решения. Таким образом, в градиентном решении в эллиптических координатах появляются классические гармоники, которые отсутствуют в классическом решении.
Для построения решения рассматриваемой задачи периодические функции Матьё, входящие в выражение (10), представим в виде ряда Фурье:
(11)
$\begin{gathered} w = \gamma ~c{\text{sh}}\xi {\text{sin}}\eta + \\ + \mathop \sum \limits_{n = 1,3,5 \ldots }^\infty \left( {~{{C}_{{1n}}}{{{\text{e}}}^{{ - n~\xi }}}\, + \,\mathop \sum \limits_{m = 1,3,5 \ldots }^\infty ~{{C}_{{2m}}}B_{n}^{m}K{{o}_{m}}(\xi ,q)~} \right)~{\text{sin}}(n~\eta ), \\ \end{gathered} $Подстановка (11) в граничные условия (3) позволяет найти коэффициенты ${{C}_{{1n}}}$ и ${{C}_{{2m}}}$. При этом для разрешимости получаемой системы уравнений необходимо использовать одинаковое количество членов ряда во внутренней и внешней суммах в (11), что соответствует тому, что в получаемом приближенном решении берется одинаковое количество гармоник, удовлетворяющих уравнению Лапласа и Гельмгольца. В общем виде получаемые граничные условия (3) после подстановки в них решения (11) для конечного числа членов ряда записываются следующим образом:
Далее необходимо приравнять нулю все соответствующие слагаемые одинаковой периодичности и получить систему уравнений. Например, при N = 1 получим систему
При N = 2:
Решение задачи, таким образом, сводится к решению линейной алгебраической системы уравнений, в которой коэффициенты вычисляются с учетом известного представления для радиальной функции Матьё через функции Бесселя [15]:
Результаты вычислений представлены на рис. 2 и 3. На рис. 2а показан характер распределения касательных напряжений вдоль оси y ($\theta = \eta = \pi {\text{/}}2$). На этой оси функции напряжений во всех рассмотренных системах координат совпадают, т.е. выполняется ${{\sigma }_{{zy}}} = {{\sigma }_{{zr}}} = {{\sigma }_{{\xi \eta }}}$. Здесь видно, что уровень максимальных напряжений, нормированных на величину заданных на бесконечности напряжений ${{\sigma }_{\infty }} = \mu ~\gamma $, в решении градиентной теории упругости оказывается ниже, чем в классическом решении, в котором напряжения монотонно затухают по закону r–2, а их максимум реализуется на границе включения, превосходя заданные напряжения ${{\sigma }_{\infty }}$ в 2 раза.
Рис. 2.
а – Распределение касательных напряжений вдоль оси y (черный цвет – решение для кругового сечения, серый цвет – решение для эллиптического включения при a/b = 2, пунктир – классическое решение для кругового сечения), б – зависимость коэффициента концентрации напряжений от относительного размера и формы поперечного сечения волокон.
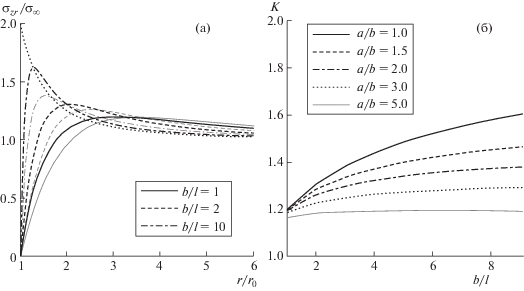
Рис. 3.
Распределение деформаций сдвига ${{\varepsilon }_{{zx}}}{\text{/}}\gamma $ (а) и ${{\varepsilon }_{{zy}}}{\text{/}}\gamma $ (б) вблизи включения с эллиптическим поперечным сечением (a/b = 2).

Из решения задачи градиентной теории упругости следует, что касательные напряжения достигают максимума на некотором расстоянии от поверхности раздела включения с матрицей, а вблизи включения снижаются, становясь равными нулю непосредственно на границе раздела. Этот результат отражает тот факт, что в рассмотренной задаче имеется дополнительное условие равенства нормальных производных от перемещений на границе раздела матрицы и включения (3). Таким образом, вследствие отсутствия деформаций сдвига на поверхности включения, касательные напряжения также равны нулю (в реальном материале, содержащем включения конечной жесткости, эти напряжения и деформации также близки к нулю). Распределение деформаций сдвига вблизи включения показано на рис. 3.
С физической точки зрения полученный результат означает, что вблизи включения имеется некоторая область материала (межфазная зона), которая, вследствие особенностей взаимодействия материалов включения и матрицы, находится в стесненном состоянии [6–8]. Протяженность “межфазной зоны” определяется в рассматриваемой модели масштабным параметром l = l2. При увеличении его относительного значения (т.е. при уменьшении размера поперечного сечения волокон) концентрация напряжений снижается и пик напряжений становится менее выраженным (рис. 2а).
Влияние эллиптичности поперечного сечения волокон a/b > 1 приводит к дополнительному снижению напряжений (рис. 2а, серые линии), что соответствует известным результатам в классических решениях, в которых, однако, максимум напряжений всегда реализуется на границе контакта. В соответствующем градиентном решении этот максимум смещается в область матрицы.
Коэффициент концентрации напряжений K = = ${{({{\sigma }_{{rz}}})}_{{{\text{max}}}}}{\text{/}}{{\sigma }_{\infty }}$ зависит от относительного размера поперечного сечения волокон b/l (или r0/l, в случае волокон с круговым сечением) и их формы, которая определяется отношением полуосей эллиптического сечения a/b. Эта зависимость показана на рис. 2б. При увеличении характерного поперечного размера волокон прогнозируется повышение концентрации напряжений. Асимптотическим значением для случая волокон большой толщины (b ≫ l) является оценка, которая может быть получена на основе решения классической задачи для эллиптического цилиндрического включения: $K = 1 + b{\text{/}}a$. Приближение градиентных решений к этим асимптотическим значениям не показано на рис. 2б, так как в этом случае реализуются очень малые значения параметра функций Матьё q, и решение становится неустойчивым (необходимо делать соответствующий предельный переход). Тем не менее, представленный диапазон значений b/l весьма интересен с точки зрения анализа влияния масштабных эффектов в композитах, содержащих волокна малой толщины. Помимо снижения концентрации напряжений, можно отметить интересный эффект, связанный с влиянием формы. Из решения следует, что эллиптичность волокон оказывает положительный эффект и приводит к снижению концентрации напряжений только в случае волокон достаточно большой толщины. Для тонких волокон (b/l = 1) этот эффект оказывается несущественным, и значения K оказываются практически одинаковыми в случае кругового сечения и эллиптического сечения при a/b = 3 (см. рис. 2б).
Как видно из построенных решений, все масштабные эффекты в рассматриваемой задаче определяются отношением характерного размера поперечного сечения волокон к масштабному параметру. Величина масштабного параметра, вообще говоря, является характеристикой материала матрицы (или дополнительной характеристикой прочности материала) и может быть определена экспериментально или теоретически, например на основе молекулярно-динамического моделирования. Для эпоксидных смол, например, известно, что масштабные параметры составляют от нескольких единиц и до нескольких десятков микрон, что при характерном размере поперечного сечения углеродных волокон 10 мкм означает, что для такого сочетания материалов отношение b/l имеет порядок единицы.
Таким образом, при малом содержании армирующих волокон и при наличии хорошего адгезионного контакта между волокнами и матрицей полученные решения позволяют прогнозировать меньшее снижение прочности однонаправленного композита вследствие концентрации напряжений при сдвиге вдоль волокон по сравнению с тем, что дает классическое решение. В классическом решении коэффициент концентрации напряжений составляет К = 2, в то время как учет стесненной зоны деформаций вблизи включений приводит к значению К = 1.2 при b/l = 1 (рис. 2а). Отсюда следует также вывод, что масштабный параметр может быть идентифицирован по результатам испытаний образцов композиционного материала путем оценки значения коэффициента концентрации напряжений K и соответствующего ему отношения b/l (в соответствии с графиками на рис. 2б) или, например, путем измерений характера распределения деформаций вблизи включений с использованием бесконтактной цифровой оптической системы и сопоставлением этих данных с моделированием (рис. 3).
Для случая больших концентраций включений целесообразно использовать более сложные формулировки модели, учитывающие взаимовлияние соседних включений и численное моделирование [12].
ЗАКЛЮЧЕНИЕ
В работе представлены новые решения для оценки напряженно-деформированного состояния в матрице вблизи жестких волокон в условиях антиплоского сдвига. Для случая тонких волокон прогнозируется снижение концентрации напряжений и соответствующее повышение прочности композиционного материала, как следствие градиентных эффектов, реализующихся вблизи границ раздела включений и матрицы. Эллиптичность поперечного сечения волокон приводит к дополнительному снижению концентрации, которое в случае тонких волокон оказывается незначительным и в прикладных расчетах им можно пренебрегать. Полученные решения и их обобщения на случай взаимодействующих волокон также могут быть использованы для оценки дополнительных масштабных параметров материала матрицы по результатам испытаний образцов композиционного материала.
Список литературы
Vasiliev V.V., Morozov E.V. Advanced mechanics of composite materials and structural elements. Newnes, 2013.
Vel S.S., Batra R.C. Three-dimensional exact solution for the vibration of functionally graded rectangular plates // J. Sound and Vibration. 2004. V. 272. № 3–5. P. 703–730.
Aboudi J. Mechanics of composite materials: a unified micromechanical approach. Elsevier, 2013.
Mindlin R.D. Micro-structure in linear elasticity // Archive for Rational Mechanics and Analysis. 1964. V. 16. № 1. P. 51–78.
Dell'Isola F., Sciarra G., Vidoli S. Generalized Hooke’s law for isotropic second gradient materials // Proc. Royal Society A: Mathematical, Physical and Engineering Sciences. 2009. V. 465. № 2107. P. 2177–2196.
Lurie S. et al. Multiscale modelling of aluminium-based metal–matrix composites with oxide nanoinclusions // Computational Materials Science. 2016. V. 116. P. 62–73.
Lurie S. et al. Interphase layer theory and application in the mechanics of composite materials // J. materials science. 2006. V. 41. № 20. P. 6693–6707.
Solyaev Y., Lurie S., Korolenko V. Three-phase model of particulate composites in second gradient elasticity // Europ. J. Mechanics-A/Solids. 2019. V. 78. P. 103853.
Ломакин Е.В. и др. Полуобратное решение задачи чистого изгиба балки в градиентной теории упругости: отсутствие масштабных эффектов // ДАН. 2018. Т. 479. № 4. С. 390–394.
Zhang Q. et al. Influence of matrix modulus on the mechanical and interfacial properties of carbon fiber filament wound composites // Rsc Advances. 2015. V. 5. № 32. P. 25 208–25 214.
Shodja H.M., Alemi B. Effective shear modulus of solids reinforced by randomly oriented-/aligned-elliptic nanofibers in couple stress elasticity. Composites Part B: Engineering, 2017. V. 117. P. 150–164. https://doi.org/10.1016/j.compositesb.2017.02.044
Lurie S., Solyaev Y., Shramko K. Comparison between the Mori-Tanaka and generalized self-consistent methods in the framework of anti-plane strain inclusion problem in strain gradient elasticity // Mechanics of Materials. 2018. V. 122. P. 133–144.
Solyaev Y., Lurie S., Semenov N. Generalized Einstein’s and Brinkman’s solutions for the effective viscosity of nanofluids // J. Applied Physics. V. 128. Iss. 4. https://doi.org/10.1063/5.0014288
Lurie S. et al. Eshelby’s inclusion problem in the gradient theory of elasticity: applications to composite materials // Intern. J. Engineering Science. 2011. V. 49. № 12. P. 1517–1525.
Абрамовиц М., Стиган И., Мак Ниш А. и др. Справочник по специальным функциям с формулами, графиками и таблицами. 1970.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Физика, технические науки