Доклады Российской академии наук. Физика, технические науки, 2021, T. 497, № 1, стр. 53-56

1. Для управления пространственной ориентацией космических аппаратов широко используют реактивные двигатели, а также гиродины. Однако первые требуют наличие рабочего тела, которое необходимо доставлять с Земли, а вторые должны постоянно находиться в движении, для чего нужна энергия. Применение подвижных внутренних масс не требует ни запаса рабочего тела, ни наличия постоянно вращающихся механических элементов [1–5]. Этот подход к задаче изменения пространственной ориентации может быть применен и в робототехнике в случаях, когда особенности внешней среды делают использование обычных внешних движителей (гусениц, колес, ног и т.п.) нежелательным.

Рассмотрим твердое тело массы M и взаимодействующее с ним конечное произвольное число N материальных точек, каждая из которых имеет массу ${{m}_{i}}$, причем $i = 1, \ldots ,N$. Применение нескольких подвижных масс для управления ориентацией твердого тела, предложенное в [6], дает преимущество при реализации управления. Предположим, что указанные объекты в начальный момент времени покоятся и в дальнейшем взаимодействуют друг с другом исключительно посредством внутренних сил, причем внешние силы полностью отсутствуют. В этом случае центр масс системы находится в состоянии покоя:

где ${{{\mathbf{R}}}_{c}}$ – радиус-вектор центра масс C твердого тела, а ${{{\mathbf{R}}}_{i}}$ – радиус-вектор материальной точки с номером i в неподвижной системе координат. Также в рассматриваемой системе сохраняется импульс: где ${{{\mathbf{v}}}_{c}}$ – вектор скорости центра масс C твердого тела, а ${{{\mathbf{v}}}_{i}}$ – вектор скорости материальной точки с номером i в неподвижной системе координат. Далее, выполняется закон сохранения кинетического момента относительно центра масс системы [6]: где вектор ${\mathbf{\omega }}$ – угловая скорость твердого тела, ${\mathbf{J}}$ – его тензор инерции относительно своего центра масс, а знак $ \times $ обозначает векторное произведение.

Если есть только одна движущаяся материальная точка массы $m$, то центр масс тела в общем случае невозможно удерживать в покое. Тогда переориентация происходит в кёниговых осях [7], т.е. в поступательно перемещающейся системе координат с началом в центре масс тела, и решение имеет вид [8]

где ${\mathbf{r}}$ – радиус-вектор материальной точки относительно точки $C$, заданный своими компонентами в неподвижной системе координат. Также в (4) использована вектор-функция ${\mathbf{\psi }}$ векторного аргумента ${\mathbf{\chi }}$причем через $(\centerdot ,\;\centerdot ,\;\centerdot )$ обозначено смешанное произведение векторов.

Пусть все материальные точки имеют один и тот же вектор скорости [6]:

где ${\mathbf{r}}_{i}^{0}$ – заданные векторы, причем $i = 1, \ldots ,N$. Показано [6], что где ${\mathbf{J}}{\kern 1pt} * = {\mathbf{J}} + {{{\mathbf{J}}}^{0}}$, а штрих означает производную по времени в подвижной системе координат, связанной с твердым телом. Используя [8] и учитывая [7] связь ${\mathbf{\dot {r}}} = {\mathbf{\omega }} \times {\mathbf{r}} + {\mathbf{r}}{\kern 1pt} '$ между абсолютной и локальной производными вектора r, из соотношения (6) получаем где компоненты вектора r заданы в неподвижной системе координат, а вектор-функция ${{\xi }_{r}} = {{\xi }_{r}}(t)$ должна иметь третью производную по времени.

Последовательность положений твердого тела в пространстве относительно кёниговой системы координат можно задать [7] с помощью ортогональной матрицы ${\mathbf{A}} = {\mathbf{A}}(t)$. Тогда компонентами вектора угловой скорости ${\mathbf{\omega }}$ в связанной с телом системе координат являются элементы кососимметрической матрицы ${\mathbf{\Omega }} = {{{\mathbf{A}}}^{{ - 1}}}{\mathbf{\dot {A}}}$. Это позволяет найти вектор ${{\xi }_{r}} = {\mathbf{J}}{\kern 1pt} {\text{*}}{\mathbf{\omega }}$ в системе координат, связанной с телом, построить его проекции на кёниговую систему координат, применить формулу (7) и спроектировать полученный в кёниговой системе координат вектор ${\mathbf{r}}$ на оси связанной с телом системы координат, тем самым определив требуемую траекторию движения подвижных масс относительно тела.

2. Потребуем, чтобы центр масс твердого тела всегда покоился. Целесообразность такого условия объясняется тем, что реальный объект, требующий изменения ориентации, как правило, представляет собой сложное устройство, включающее в себя самые разные элементы. Для части из них колебания, вызываемые перемещением подвижных масс, могут быть вредны. Например, космический аппарат может иметь антенны, колебания которых могут привести к сбоям в работе разнообразного оборудования. В случае, когда речь идет о робототехнической системе, перемещающейся в ранимой среде, необязательные вибрации, связанные с работой системы переориентации, могут нанести этой среде дополнительные повреждения.

Подставим в уравнение (3) вектор $M{{{\mathbf{v}}}_{c}}$ из соотношения (2):

Поскольку в (1) функция ${{{\mathbf{R}}}_{c}} = {{{\mathbf{R}}}_{c}}(t) \equiv 0$, то

3. Рассмотрим задачу нахождения траекторий движения материальных точек из соотношений (9) при заданном векторе $\xi = \xi (t)$ при N = 2. На основании (9) имеем

Из уравнения (10) получаем

Сравним варианты (11) и (4) в случае, когда m₁ = = m₂ = $\frac{m}{2}$. Тогда можно сопоставить векторы R₁ и r. Они всегда сонаправлены, а отношение их модулей равно

Из формулы (12) видно, что в случае использования одной материальной точки ее всегда нужно смещать больше, чем каждую из двух точек с той же суммарной массой. Заметим, что отношение (12) стремится к единице с ростом массы тела M по сравнению с m. Например, величина $\zeta \approx 0.95$ при $\frac{m}{M} = 0.10$. Другое отличие состоит в том, что в случае использования двух подвижных материальных точек нет надобности в учете массы твердого тела, поскольку величина M не входит в соотношения (11).

4. Если число подвижных точечных масс равно трем, то решений бесконечно много. Например, найдем одно из них, представив, скажем, третью из масс как две, т.е. перейдем к задаче с четырьмя массами. Для этого запишем условие (9) как систему из четырех уравнений

где сумма масс ${{m}_{3}} + {{m}_{4}}$ равна величине третьей подвижной массы и

Решение системы (13), (14) имеет вид

Заметим, что все три массы всегда находятся на одной и той же прямой. Величины ${{\lambda }_{i}} > 0$, $i = 1$, ..., 4, можно найти с помощью условий

где первые два равенства обеспечивают неподвижность центра масс твердого тела, а последнее равенство отражает тот факт, что третья и четвертая материальные точки соответствуют одной и той же подвижной массе и должны всегда находиться в одной и той же точке пространства. Из формул (14)–(16) получаем следующую систему уравнений для поиска значений ${{\lambda }_{i}}$, $i = 1, \ldots ,4$:

Из соотношений (17) имеем

Аналогичным способом можно найти решение в случае произвольного конечного числа подвижных масс.

5. Описанный выше способ неприменим, если в какой-либо момент времени смешанное произведение $({\mathbf{\chi }},\;{\mathbf{\dot {\chi }}},\;{\mathbf{\ddot {\chi }}})$ положительно, поскольку тогда функция (5) не определена. Она не определена и в случае, когда векторы ${\mathbf{\chi }}$ и ${\mathbf{\dot {\chi }}}$ коллинеарны. Укажем другой подход, который позволяет решить задачу и при указанных обстоятельствах. Для этого обратим внимание на то, что необязательно заменять систему уравнений (9) системой типа (13). Можно вместо (13) применять соотношения

Заметим, что в этом случае векторы ${{{\mathbf{R}}}_{i}}$ будут направлены не коллинеарно одному и тому же вектору ${\mathbf{\psi }}(\xi )$, а коллинеарно векторам ${\mathbf{\psi }}({{\lambda }_{i}}{{\xi }_{i}})$. Далее для простоты рассмотрим использование этого подхода на следующем примере. Пусть имеются шесть подвижных одинаковых масс, каждая из которых равна $m{\text{/}}6$. Потребуем, чтобы

Условие (20) обеспечивает неподвижность центра масс твердого тела. Тогда решение системы (19) можно свести к решению трех уравнений

где векторы ${{\xi }_{j}}$ направлены вдоль координатных осей некоторой ортогональной неподвижной системы координат с центром в центре масс твердого тела. В этом случае векторы ${{\xi }_{j}}$ и ${{\dot {\xi }}_{j}}$ всегда коллинеарны.

Введем вектор-функцию [8]

где вектор-функция ${\mathbf{\eta }} = {\mathbf{\eta }}(t)$ должна иметь вторую производную по времени, а смешанное произведение $\left( {{\mathbf{\chi }},{\mathbf{\eta }},{\mathbf{\dot {\eta }}}} \right)$ должно быть отрицательным. Без ограничения общности можно полагать, что вектор ${\mathbf{\eta }}$ лежит в плоскости, ортогональной векторам $\chi $ и $\dot {\chi }$, и является единичным. В этом случае векторы ${\mathbf{\eta }}$ и ${\mathbf{\dot {\eta }}}$ всегда ортогональны, а их векторное произведение коллинеарно вектору $\chi $. С помощью (22) решение системы уравнений (21) можно записать в форме [8] где для каждого значения j = 1, 2, 3 соответствующий дважды дифференцируемый вектор ${{{\mathbf{\eta }}}_{j}} = {{{\mathbf{\eta }}}_{j}}(t)$ лежит в плоскости, ортогональной вектору ${{\xi }_{j}}$, причем векторы ${{\xi }_{j}}$, ${{{\mathbf{\eta }}}_{j}}$ и ${{{\mathbf{\dot {\eta }}}}_{j}}$ образуют левую тройку. Таким образом, каждый из векторов ${{{\mathbf{\eta }}}_{j}}$ зависит от одной скалярной функции времени, которую можно выбирать произвольно с учетом описанных условий. Приняв во внимание (20), получаем, что каждая из трех пар материальных точек должна перемещаться симметрично относительно центра масс твердого тела в плоскости, ортогональной соответствующей оси координат. При выполнении этого условия траекторию движения и скорость перемещения для любой пары можно выбирать по-разному за счет выбора вектор-функции ${{{\mathbf{\eta }}}_{j}}$, но так, чтобы в итоге получался нужный кинетический момент согласно формуле (23). Например, возьмем составляющую ${{\xi }_{3}}$. Условие $({{{\mathbf{\chi }}}_{3}},{{{\mathbf{\eta }}}_{3}},{{{\mathbf{\dot {\eta }}}}_{3}})$ < 0 дает

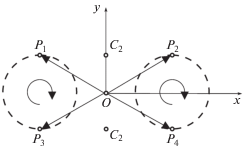
Значение дроби в (24) равно тангенсу полярного угла, описывающего вектор ${{{\mathbf{\eta }}}_{3}}$ в неподвижной системе координат, лежащей в плоскости, ортогональной вектору ${{\xi }_{3}}$. Если, скажем, в течение всего времени движения ${{\xi }_{{3z}}} > 0$, то этот тангенс должен все время убывать, что возможно лишь тогда, когда рассматриваемая пара материальных точек вращается вокруг оси аппликат неподвижной системы координат. Но это не всегда удобно с точки зрения реализации. В этом случае можно заменить эту пару материальных точек, например, на систему из четырех подвижных масс так, чтобы вокруг оси вращались центры масс двух систем, каждая из которых состоит из двух точек. Тогда последние не обязаны двигаться вокруг центра масс твердого тела. В качестве примера на рис. 1 показаны четыре материальные точки P_i, $i = 1, \ldots ,4$, одинаковой массы. Каждая из пар точек ${{P}_{1}}$, ${{P}_{3}}$ и ${{P}_{2}}$, ${{P}_{4}}$ вращается с одинаковой угловой скоростью в направлении, показанном стрелками, в плоскости $Oxy$ неподвижной системы координат по окружностям одинакового радиуса, показанным штриховыми линиями и находящимся на равных расстояниях от центра масс системы O, совпадающем с центром масс твердого тела C. Тогда центры масс ${{C}_{1}}$ и ${{C}_{2}}$ пар ${{P}_{1}}$, ${{P}_{3}}$ и ${{P}_{2}}$, ${{P}_{4}}$ соответственно вращаются вокруг центра масс системы O.