Доклады Российской академии наук. Физика, технические науки, 2021, T. 497, № 1, стр. 49-52

Рассматриваются нелинейные волны малой амплитуды в упругих стержнях, когда имеется сильное взаимодействие продольных и крутильных движений. Ранее эти движения рассматривались независимо [1–6], а в некоторых случаях рассматривалось частичное взаимодействие этих движений [7]. В [8] была выписана гиперболическая система уравнений, выражающая законы сохранения продольного импульса и момента импульса и рассмотрены простые волны и образование разрывов. В [9, 10] были исследованы возможные разрывы в решениях этих уравнений на основе соотношений, обеспечивающих выполнение упомянутых законов сохранения. Была исследована ударная адиабата и неравенства между скоростью разрыва и скоростями малых возмущений по обе стороны разрыва. Как известно, кроме существования разрывов типа ударных волн, на которых выполняются соотношения, следующие из законов сохранения и обеспечивающие их эволюционность [11, 12], возможны разрывы, называемые особыми [13], соотношения на которых представлены, помимо соотношений, следующих из законов сохранения, некоторыми дополнительными соотношениями [14]. При теоретическом изучении дополнительные соотношения могут быть получены как условия существования стационарной структуры разрыва [15].

В предлагаемой работе, с целью изучения возможностей реализации разрывов обоих типов, изучается решение задачи о структуре разрывов в предположении, что главный механизм, определяющий структуру – вязкость.

Рассмотрим случай, когда при распространении волн в стержнях нелинейные эффекты происходят за счет нелинейной связи напряжений и деформаций, причем последние считаются малыми. Упругую энергию единицы лагранжевой длины стержня будем считать представленной в виде кубического многочлена от деформаций (растяжения u₁ и закрутки u₂), а кинетическую энергию – в виде квадратичной формы c диагональной матрицей коэффициентов от скоростей ${{{v}}_{1}}$ и ${{{v}}_{2}}$:

Здесь $q = q(x,t)$ – перемещения вдоль оси стержня, $x$ – лагранжева координата вдоль оси стержня, $t$ – время, $\varphi = \varphi (x,t)$ – угол поворота сечения стержня.

Если ввести новые переменные, отличающиеся от пар переменных ${{u}_{1}},\;{{{v}}_{1}}$ и ${{u}_{2}},\;{{{v}}_{2}}$ подходящим образом подобранными множителями λ₁ и λ₂, то уравнения движения можно записать в виде (для новых переменных оставлены прежние обозначения)

Уравнения (2) представляют усредненные по сечению стержня уравнения нелинейной вязко-упругости, выражающие сохранение продольного импульса и момента импульса вокруг оси стержня. В уравнениях (2) по сравнению с уравнениями, использовавшимися в [10], учтены вязкие напряжения с постоянными коэффициентами вязкости ${{\mu }_{1}}$, ${{\mu }_{2}}$. Форма (3) принятой внутренней энергии F(u₁, ${{u}_{2}})$ обусловлена предположением о четности функции F по переменной ${{u}_{2}}$.

Под структурой разрыва будем понимать решение ${{u}_{i}}(\xi ),$ ${{{v}}_{i}}(\xi )$ уравнений (2), где $\xi = - x + Wt$, $W = {\text{const}} > 0$. При $\xi \to \pm \infty $ решение стремится к предельным значениям. Из уравнений (2) следуют обыкновенные дифференциальные уравнения для структуры, из которых, после однократного интегрирования и исключения переменных ${{{v}}_{1}}$ и ${{{v}}_{2}}$, получаем систему уравнений для переменных u₁ и u₂. Введем вместо переменных u₁ и u₂ переменные Y₁ и Y₂ и вместо переменной ξ переменную $\eta $. Таким образом уравнения (2) примут вид

Здесь

Начальное состояние при $\eta = - \infty $ задается равенствами ${{Y}_{1}} = 1$, ${{Y}_{2}} = 1$ и соответствует состоянию перед структурой. На плоскости Y₁, Y₂ начальная точка ${{Y}_{1}} = 1$, ${{Y}_{2}} = 1$ является особой точкой системы (4), (5) и одновременно стационарной точкой функции $N({{Y}_{1}},{{Y}_{2}})$. Другие особые точки этой системы могут представлять состояние за структурой (разрывом). Цель предлагаемого исследования состоит в нахождении условий, при которых особые точки системы (4), (5) на плоскости Y₁, Y₂ соединяются интегральными кривыми. Отметим, что согласно (4), (5) функция $N({{Y}_{1}}(\eta ),$ ${{Y}_{2}}(\eta ))$ убывает с ростом η: $\frac{{dN}}{{d\eta }}$ < 0.

Отметим также, что значения скоростной переменной s (см. (7)), соответствующие малым возмущениям $s = {{s}_{1}}$ и $s = {{s}_{2}}$, находятся как собственные значения матрицы вторых производных функции $N({{Y}_{1}},{{Y}_{2}})$ и удовлетворяют уравнению

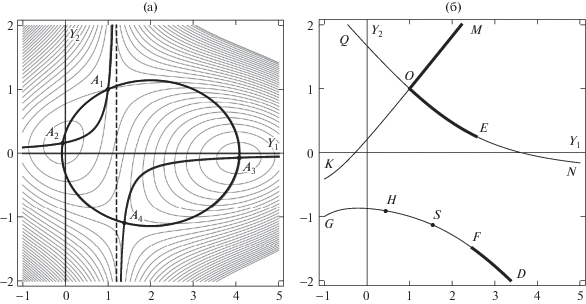
Рассмотрим особые точки и интегральные кривые системы (4), (5) в случае, когда $P > 0$. Уравнения ${{N}_{1}} = 0$ и ${{N}_{2}} = 0$ представляют на плоскости ${{Y}_{1}},{{Y}_{2}}$ эллипс и гиперболу, которые проходят через начальную точку ${{Y}_{1}} = 1$, ${{Y}_{2}} = 1$ и представляют изоклины линий уровня функции $N({{Y}_{1}},{{Y}_{2}})$. Типичный вид линий уровня функции $N({{Y}_{1}},{{Y}_{2}})$ = const с начальной точкой A₁ изображен на рис. 1а.

Рис. 1.

Линии уровня (а) и ударная адиабата (б). $\kappa = 2$, $P = 0.6$, s = 1.2.

Упомянутые изоклины изображены более толстыми линиями. Штриховой линией обозначена вертикальная асимптота гиперболы. Точки A₁, A₄ – седла (как для функции N, так и для уравнений (4), (5)), A₂ – максимум функции $N$ и одновременно узел для системы (4), (5) с выходящими с ростом $\eta $ интегральными кривыми, A₃ – минимум функции $N$ и узел с входящими в него интегральными кривыми.

Направление движения точки по интегральным кривым с ростом $\eta $ при всех значениях m = = $\frac{{{{\mu }_{1}}}}{{\kappa {{\mu }_{2}}}}$ принадлежит тому же квадранту плоскости ${{Y}_{1}},{{Y}_{2}}$, что и вектор $ - {\text{grad}}N$. В области внутри эллипса между ветвями гиперболы (рис. 1) направления движения точки по интегральным кривым с ростом $s$ принадлежат четвертому квадранту. При малых значениях m интегральные кривые почти горизонтальны, а при больших значениях $m$ – почти вертикальны. Это означает существование такого значения $m = {{m}_{a}}(s)$, при котором седла ${{A}_{1}}$ и ${{A}_{4}}$ соединены интегральной кривой, представляющей структуру особого разрыва. Интегральная кривая ${{A}_{1}} \to {{A}_{4}}$ (седло–седло) может существовать только при $s > 1$, поскольку при $s < 1$ выполняется неравенство $N({{A}_{1}}) < N({{A}_{4}})$, противоречащее убыванию функции $N$ с ростом $s$. На рис. 2 представлен график ${{m}_{a}}(s)$, полученный численно для $\kappa $ = 2, $P = 0.6$, $s = 1.2$ на интервале $1 < s < s_{2}^{ - }$ (кривая $a$).

Рис. 2.

Функция m(s).

Соединение седел ${{A}_{1}}$ и ${{A}_{4}}$ при $s > {{s}_{2}}$, когда начальная точка ${{A}_{2}}(1,1)$ – выходящий узел, определяет граничное значение ${{m}_{b}}(s)$, такое, что при $m < {{m}_{b}}(s)$ точки ${{A}_{2}}$ и ${{A}_{4}}$ соединяются интегральной кривой, представляющей структуру быстрой ударной волны, а при $m > {{m}_{b}}(s)$ сепаратриса точки ${{A}_{1}}$ проходит между точек ${{A}_{2}}$ и ${{A}_{4}}$ и структура ударной волны ${{A}_{2}} \to {{A}_{4}}$ не существует.

На рис. 2 представлен график функции ${{m}_{b}}(s)$ (кривая $b$), непрерывно продолжающий график функции ${{m}_{a}}(s)$ (кривая $a$), хотя аналитически это другая функция. Функция ${{m}_{b}}(s)$ построена численно при тех же параметрах, что и функция ${{m}_{a}}(s)$. Если задано значение m* и $m{\kern 1pt} * < {{m}_{{{\text{min}}}}}$, то при $s > {{s}_{2}}$ структура разрывов типа ${{A}_{2}} \to {{A}_{4}}$ существует при всех $s$. Если $m{\kern 1pt} * > {{m}_{{{\text{min}}}}}$, то существует такое значение $s = {{s}_{*}}$, что при $s < {{s}_{*}}$ структура разрыва типа ${{A}_{2}} \to {{A}_{4}}$ не существует, а при $s > {{s}_{*}}$ – структура этого разрыва существует. При том же неравенстве $m{\kern 1pt} * > {{m}_{{{\text{min}}}}}$ существует структура особого разрыва при $s = s{\kern 1pt} *$ (рис. 2).

На рис. 1б изображен один из вариантов качественно различных ударных адиабат, исследованных в [10] ($0 < P < 1$, $\kappa > 2 - P$), построенный численно для параметров $\kappa = 2$, $P = 0.6$, $s = 1.2$. Ударная адиабата (множество состояний за разрывами из начальной точки O) содержит три ветви – $QN$, $KM$ и $GD$. На ударной адиабате жирными линиями отмечены части ударной адиабаты, соответствующие разрывам со структурой. Изображен случай $m{\kern 1pt} * > {{m}_{{{\text{min}}}}}$. Части ударной адиабаты $OM$ и $FD$ соответствуют состояниям за быстрыми ударными волнами, имеющим структуру, SF – за эволюционными быстрыми ударными волнами без структуры, OE – за медленными ударными волнами (все они имеют структуру). Точкой $H$ отмечено состояние за особым разрывом. Если $m{\kern 1pt} * < {{m}_{{{\text{min}}}}}$, то особого разрыва не будет, и весь эволюционный участок $SD$ будет соответствовать быстрым ударным волнам со структурой. Остальные части ударной адиабаты не могут реализовываться либо в силу неустранимой неэволюционности, либо из-за типов особых точек, не позволяющих образоваться структуре. Исследование структуры разрывов при других значениях параметров P и $\kappa $ проводится аналогичным образом и будет опубликовано позднее.