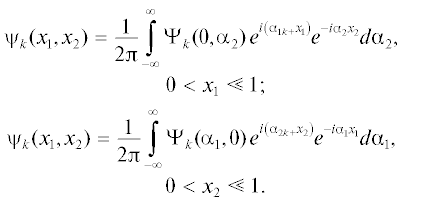1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Физика, технические науки
  4. T. 498, № 1, 2021

Доклады Российской академии наук. Физика, технические науки, 2021, T. 498, № 1, стр. 33-39

БЛОЧНЫЕ ЭЛЕМЕНТЫ В ГРАНИЧНЫХ ЗАДАЧАХ ДЛЯ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ МЕХАНИКИ И ФИЗИКИ В НЕКЛАССИЧЕСКИХ ОБЛАСТЯХ

Академик РАН В. А. Бабешко 1, 2, *, О. В. Евдокимова 1, О. М. Бабешко 2

1 Федеральный исследовательский центр Южный научный центр Российской академии наук
Ростов-на-Дону, Россия

2 Кубанский государственный университет
Краснодар, Россия

* E-mail: babeshko41@mail.ru

Поступила в редакцию 16.03.2021
После доработки 09.04.2021
Принята к публикации 12.04.2021

Полный текст (PDF)

Аннотация

В настоящей работе развивается новый, строго обоснованный подход, позволяющий значительно расширить класс граничных задач для линейных систем дифференциальных уравнений в частных производных с постоянными коэффициентами в неклассических областях, которые можно точно решать методом блочного элемента. Разработанный в методе блочного элемента новый, координатный, дополняющий интегродифференциальный, метод удовлетворения граничных условий завершает построение точных решений исходных граничных задач, разложенных по блочным элементам. Подход охватывает многие системы уравнений в частных производных с постоянными коэффициентами механики деформируемого твердого тела, гидромеханики, электромагнитных полей и других наук, для которых можно строить точные решения граничных задач в неклассических областях. Приводятся примеры реализации подхода.

Ключевые слова: метод блочного элемента, граничные задачи, системы дифференциальных уравнений, термоупругость, преобразование Галёркина, уравнения Ламе

В более ранней работе авторов развит интегродифференциальный метод решения некоторых граничных задач для систем дифференциальных уравнений в частных производных, основанный на блочных элементах. В работе [1] построено решение векторной граничной задачи, разложенное по упакованным блочным элементам, которые являются решениями скалярных граничных задач для потенциальной и векторной составляющих уравнения Ламе в первом квадранте. Решения ряда векторных дифференциальных уравнений в частных производных механики сплошных сред, электромагнитных явлений, теории поля допускают более общие представления в виде разложений по решениям скалярных уравнений, чем описанное представление. В его основе лежит преобразование Галёркина [2]. Этот подход удобен и использовался при решении задач во всем пространстве и в ряде классических областей. К ним относятся такие области, как полупространство, шар, цилиндр, а также в некоторых областях, получаемых в результате представлений групп преобразований пространства [3–5]. В то же время для ряда важных областей, отличных от классических, например, клиновидных, прямоугольных, в форме полуполос и полуплит, построение точных решений этим подходом пока не удавалось осуществить. Исследованию граничных задач для уравнения Ламе посвящено огромное количество работ, содержащих как аналитические, так и численные исследования, выполненные более чем за полтора века. Все публикации в этой области невозможно охватить. Отметим те из них, где удавалось построить точные аналитические решения некоторых типов граничных задач для векторных уравнений Ламе в неклассических областях. Опустим из рассмотрения многочисленные работы, посвященные граничным задачам в полупространстве и слоистой среде, где преобразование Фурье решает проблему. В сферических, цилиндрических областях следует отметить работы, посвященные построению собственных векторных функций [6–8]. Этот подход развивался для применения в цилиндрических, эллиптических, клиновидных, конических областях. Основная сложность при решении граничных задач этим подходом в неклассических областях состоит в трудности удовлетворения граничных условий.

В то же время построение точных решений граничных задач в практических применениях позволяет выявлять свойства и явления, которые оказывались упущенными при использовании различных приближенных подходов. Так, разработанный недавно метод блочного элемента позволил выявить условия возникновения некоторых типов землетрясений [9, 10]. Этот же метод дал возможность обнаружить существование нового типа трещин, дополняющих трещины Гриффитса [11].

В работе авторов [1] разложение решения векторной граничной задачи с помощью скалярных было построено интегродифференциальным методом. В работе [12] развит иной подход, названный координатным, также основанный на методе блочного элемента. Он применен к уравнениям Ламе в четверти плоскости, опираясь на представление решения в виде потенциальной и вихревой составляющих. В указанной работе построено доступное для дальнейшего анализа точное решение в первом квадранте двумерной граничной задачи для динамических уравнений Ламе при произвольных граничных условиях в дополнение к [1]. Однако представление решения граничной задачи в виде потенциальной и вихревой составляющих ограничивает применение метода блочного элемента к граничным задачам для других систем дифференциальных уравнений. В работе [13] эта сложность преодолевается применением к изучаемым системам дифференциальных уравнений преобразований Галёркина, позволяющих представлять решения векторных граничных задач в форме не связанных отдельных скалярных уравнений. В настоящей работе дается строгое обоснование применения этого метода в граничных задачах, опираясь на теорему Боджно [14].

ПОСТАНОВКА ЗАДАЧИ

1. В публикации авторов [1] рассматривалась двумерная граничная задача первого рода в первом квадранте $\Omega $ для системы уравнений Ламе в предположении гармонических во времени воздействий на границе.

Для удовлетворения граничных условий при ее исследовании блочными элементами был разработан интегродифференциальный метод. Ее уравнения имеют вид

$\begin{gathered} \left( {\lambda + \mu } \right)\frac{{\partial \theta }}{{\partial {{x}_{1}}}} + \mu \Delta {{u}_{1}} = 0,\quad \theta = \frac{{\partial {{u}_{1}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{u}_{2}}}}{{\partial {{x}_{2}}}}, \\ \left( {\lambda + \mu } \right)\frac{{\partial \theta }}{{\partial {{x}_{2}}}} + \mu \Delta {{u}_{2}} = 0,\quad {{x}_{1}},{{x}_{2}} \in \Omega , \\ \Delta u = \frac{{{{\partial }^{2}}u}}{{\partial x_{1}^{2}}} + \frac{{{{\partial }^{2}}u}}{{\partial x_{2}^{2}}}. \\ \end{gathered} $

Здесь ${{u}_{n}}({{x}_{1}},{{x}_{2}})$ – компоненты векторов перемещений в точке ${{x}_{1}}$, ${{x}_{2}}$, Ω – область первого квадранта ${{x}_{1}} \geqslant 0$, ${{x}_{2}} \geqslant 0$, λ, μ – параметры Ламе. В задаче типа Дирихле на границе первого квадранта задаются компоненты векторов перемещения ${{u}_{1}}({{x}_{1}},0)$, ${{u}_{2}}\left( {{{x}_{1}},0} \right)$ и ${{u}_{1}}\left( {0,{{x}_{2}}} \right)$, ${{u}_{2}}(0,{{x}_{2}})$. Для удовлетворения граничных условий при ее исследовании блочными элементами был разработан интегродифференциальный метод. Решение граничной задачи для системы уравнений Ламе разлагалось на потенциальную и вихревую составляющие.

Ниже приводится другой, более общий метод исследования и решения граничных задач для систем дифференциальных уравнений в неклассических областях, опирающийся на преобразование Галёркина. Метод демонстрируется на примерах как рассмотренной ранее граничной задаче для уравнений Ламе, так и более сложной граничной задаче для системы дифференциальных уравнений термоупругости. Продемонстрируем применение преобразования Галёркина на примере ранее рассмотренных уравнений Ламе. Для удобства применения преобразования Галёркина запишем трехмерные уравнения Ламе в следующей форме [3]:

$\mu \Delta {\mathbf{u}} + (\lambda + \mu ){\text{grad}}\,{\text{div}}{\mathbf{u}} = 0.$

Следуя [3], введем обозначения

(1)
$\begin{gathered} {{L}_{{mn}}}({{u}_{n}}) = 0,\quad {{L}_{{mn}}} = {{\delta }_{{mn}}}\Delta + \sigma \partial _{m}^{2}\partial _{n}^{2},\quad m,n = 1,\;2,\;3, \\ \sigma = {{\mu }^{{ - 1}}}(\lambda + \mu ),\quad \partial _{m}^{h} = \frac{{{{\partial }^{h}}}}{{\partial x_{m}^{h}}}, \\ \end{gathered} $
δij – символ Кронекера.

Осуществим преобразование Галёркина, положив

$\begin{gathered} {{u}_{1}} = \left| {\begin{array}{*{20}{c}} {{{\chi }_{1}}}&{{{L}_{{12}}}}&{{{L}_{{13}}}} \\ {{{\chi }_{2}}}&{{{L}_{{22}}}}&{{{L}_{{23}}}} \\ {{{\chi }_{3}}}&{{{L}_{{32}}}}&{{{L}_{{33}}}} \end{array}} \right|,\quad {{u}_{2}} = \left| {\begin{array}{*{20}{c}} {{{L}_{{11}}}}&{{{\chi }_{1}}}&{{{L}_{{13}}}} \\ {{{L}_{{21}}}}&{{{\chi }_{2}}}&{{{L}_{{23}}}} \\ {{{L}_{{21}}}}&{{{\chi }_{3}}}&{{{L}_{{33}}}} \end{array}} \right|, \\ {{u}_{3}} = \left| {\begin{array}{*{20}{c}} {{{L}_{{11}}}}&{{{L}_{{12}}}}&{{{\chi }_{1}}} \\ {{{L}_{{21}}}}&{{{L}_{{22}}}}&{{{\chi }_{2}}} \\ {{{L}_{{21}}}}&{{{L}_{{32}}}}&{{{\chi }_{3}}} \end{array}} \right| \\ \end{gathered} $
и затем внесем эти определители в систему уравнений. Обозначим ${{T}_{i}} = \Delta {{\chi }_{i}}$ и осуществим упрощения. В результате приводим систему к бигармоническим уравнениям, имеющим вид $\Delta \Delta {{T}_{i}}$ = 0, которые составлены относительно функций Галёркина Ti. Здесь ${{\Delta }}$ – двумерный оператор Лапласа.

Дополнительным исследованием определяются граничные условия для функций Ti, исходя из первоначальных, заданных для системы уравнений.

Аналогичным преобразованием Галёркина строятся скалярные, т.е. не связанные, отдельные дифференциальные уравнения для практически всех систем уравнений механики деформируемого твердого тела и гидромеханики, электромагнитных эффектов, теории поля и других наук. В излагаемом подходе, при применении преобразований Галёркина, требуется построить граничные условия для функций полученных скалярных уравнений. Они должны вытекать из первоначально заданных граничных условий. Кроме этого, возможно наличие некоторых зависимостей между функциями Галёркина. С этими проблемами встречаются исследователи, применяющие как аналитические, так и численные методы. Метод блочного элемента позволяет решать эти проблемы.

2. Динамическая задача о температурных напряжениях при гармонических воздействиях на границе [4]. В форме, аналогичной использованной выше, четыре уравнения термоупругости, составленные относительно перемещений ${{u}_{n}}$, $n = 1,2,3$, и температуры $\theta $, имеют вид

(2)
$\begin{gathered} {{L}_{{mn}}}({{u}_{n}}) + {{L}_{{m4}}}(\theta ) = 0,\quad {{L}_{{4n}}}({{u}_{n}}) + {{L}_{{44}}}(\theta ) = 0, \\ {{L}_{{mn}}} = {{\delta }_{{mn}}}\square \,_{2}^{2}\, + (\lambda + 2\mu ){{\mu }^{{ - 1}}}\partial _{m}^{2}\partial _{n}^{2}, \\ m = 1,2,3,4,\quad n = 1,2,3, \\ \partial _{m}^{h} = \frac{{{{\partial }^{h}}}}{{\partial x_{m}^{h}}},\quad {{L}_{{m4}}} = - \gamma {{\mu }^{{ - 1}}}\partial _{m}^{1},\quad {{L}_{{4n}}} = - \eta \partial _{t}^{1}\partial _{n}^{1}, \\ \partial _{t}^{h} = \frac{{{{\partial }^{h}}}}{{\partial {{t}^{h}}}},\quad {{L}_{{44}}} = \,\,\square \,_{3}^{2},\quad \square \,_{p}^{2}\,\, \equiv \Delta - \left( {\frac{1}{{c_{p}^{2}}}} \right)\partial _{t}^{2},\quad p = 1,2, \\ \square \,_{3}^{2}\,\, \equiv \Delta - \left( {\frac{1}{{c_{3}^{2}}}} \right)\partial _{t}^{1},\quad c_{3}^{2} = \frac{{{{\lambda }_{0}}}}{{{{c}_{\varepsilon }}}}. \\ \end{gathered} $

Здесь Δ – оператор Лапласа. Остальные введенные параметры являются постоянными характеристиками деформационных и тепловых процессов в рассматриваемом теле, их значения объяснены в [4].

Применим преобразование Галёркина. Для этого введем новые неизвестные с помощью определителей

$\begin{gathered} {{u}_{1}} = \left| {{\mathbf{\chi }}{\text{,}}{{{\mathbf{K}}}_{{12}}}{\text{,}}{{{\mathbf{K}}}_{{13}}}{\text{,}}{{{\mathbf{K}}}_{{14}}}} \right|{\text{,}}\quad {{u}_{2}} = \left| {{{{\mathbf{K}}}_{{11}}}{\text{,}}{\mathbf{\chi }}{\text{,}}{{{\mathbf{K}}}_{{13}}}{\text{,}}{{{\mathbf{K}}}_{{14}}}} \right|, \\ {{u}_{3}} = \left| {{{{\mathbf{K}}}_{{11}}}{\text{,}}{{{\mathbf{K}}}_{{12}}}{\text{,}}{\mathbf{\chi }}{\text{,}}{{{\mathbf{K}}}_{{14}}}} \right|,\quad {{u}_{4}} = \left| {{{{\mathbf{K}}}_{{11}}}{\text{,}}{{{\mathbf{K}}}_{{12}}}{\text{,}}{{{\mathbf{K}}}_{{13}}}{\text{,}}{\mathbf{\chi }}} \right|, \\ \end{gathered} $

Столбцами определителей являются векторы

${\mathbf{\chi }} = {{\chi }_{n}},\quad {{{\mathbf{K}}}_{{1n}}} = {{L}_{{mn}}},\quad m,n = 1,\;2,\;3,\;4.$

Получаем четыре независимых уравнения, которые имеют вид

$\left| {{{L}_{{mn}}}} \right|{{\chi }_{n}} = 0.$

Участвующий в этом уравнении определитель представляет, после его раскрытия, дифференциальные уравнения. Введя новые функции, обозначив ${{\varphi }_{n}} = \,\,\square \,_{2}^{2}{{\chi }_{n}}$, $n = 1,\;2,\;3$, $\psi = \,\,\square \,_{2}^{2}{{\chi }_{4}}$, приходим к системе независимых скалярных уравнений

(3)
$\begin{gathered} \square \,_{2}^{2}[\square \,_{1}^{2}\square \,_{3}^{2}\, - \eta \partial _{t}^{1}\Delta ]{{\varphi }_{m}} = 0,\quad m = 1,2,3, \\ [\square \,_{1}^{2}\square \,_{3}^{2}\, - m\eta \partial _{t}^{1}\Delta ]\psi = 0. \\ \end{gathered} $

Граничные условия для новых функций формируются на основе применения формул перехода от старых неизвестных к новым на границе.

МЕТОД РЕШЕНИЯ

1. В работе [13] изложены три различных подхода к решению скалярных граничных задач методом блочного элемента. Они были названы “прямой метод”, “метод расщепления операторов” и “метод подстановок”. В зависимости от исходных целей исследования рассматриваемой граничной задачи может приниматься любой из трех подходов. Прямой метод дает решение граничной задачи наиболее компактными формулами. Однако они оказываются достаточно сложными для анализа решения.

Метод расщепления операторов представляет решение граничной задачи для системы уравнений разложенным по решениям некоторых граничных задач, которые требуют дополнительных преобразований граничных условий.

Наиболее простым в представлении решения исходной граничной задачи является метод подстановок, восходящий к теореме Боджно [14], которая утверждает, что самым общим решением уравнения

${{D}_{1}}{{D}_{2}}\; \ldots \;{{D}_{{n - 1}}}{{D}_{n}}\varphi = 0,$
где Dk, $k = 1,2, \ldots ,n$, – некоторые операторы, является функция
$\varphi = {{\varphi }_{1}} + {{\varphi }_{2}} + \; \ldots \; + {{\varphi }_{{n - 1}}} + {{\varphi }_{n}},$
если функции φm удовлетворяют уравнениям

${{D}_{m}}{{\varphi }_{m}} = 0,\quad m = 1,2,\; \ldots ,\;n.$

2. В качестве примера рассмотрим решение одной из двумерных граничных задач для одного из уравнений (3) в предположении гармонических, описываемых временной функцией ${{e}^{{ - i\omega t}}}$ воздействий на границы первого квадранта. Исключая в уравнениях и граничных условиях временной множитель, получим уравнение вида

(4)
$[\square \,_{1}^{2}\square \,_{3}^{2}\, + i\omega m\eta \Delta ]\psi = 0.$

В результате упрощения уравнения (4) получаем следующее его представление в форме произведения операторов Гельмгольца D1 и D2:

$\begin{gathered} {{D}_{1}}{{D}_{2}}\psi = 0, \\ {{D}_{1}} = \Delta + p_{1}^{2},\quad {{D}_{2}} = \Delta + p_{2}^{2}, \\ p_{1}^{2} = {{b}_{1}} - \sqrt {b_{1}^{2} - {{b}_{2}}} ,\quad p_{2}^{2} = {{b}_{1}} + \sqrt {b_{1}^{2} - {{b}_{2}}} , \\ 2{{b}_{1}} = {{\omega }^{2}}\left( {\frac{1}{{c_{1}^{2}}}} \right) + i\omega \left[ {\left( {\frac{1}{{c_{3}^{2}}}} \right) + m\eta } \right], \\ {{b}_{2}} = i{{\omega }^{3}}\left( {\frac{1}{{c_{3}^{2}}}} \right)\left( {\frac{1}{{c_{1}^{2}}}} \right). \\ \end{gathered} $

Таким образом, в соответствии с теоремой Боджно необходимо построить решения граничных задач ${{D}_{m}}{{\psi }_{m}} = 0$, $m = 1,\;2$.

Рассмотрим случай, когда для функции $\psi ({{x}_{1}},{{x}_{2}})$ на границе первого квадранта поставлены следующие граничные условия:

(5)
$\begin{gathered} \psi ({\text{0,}}{{x}_{{\text{2}}}}) = u({\text{0,}}{{x}_{{\text{2}}}}){\text{,}}\quad {{\partial }_{{\text{1}}}}\psi ({\text{0,}}{{x}_{{\text{2}}}}) = {{\partial }_{{\text{1}}}}u({\text{0,}}{{x}_{{\text{2}}}}); \\ \psi ({{x}_{{\text{1}}}}{\text{,0}}) = u({{x}_{{\text{1}}}}{\text{,0}}){\text{,}}\quad {{\partial }_{{\text{2}}}}\psi ({{x}_{{\text{1}}}}{\text{,0}}) = {{\partial }_{{\text{2}}}}u({{x}_{{\text{1}}}}{\text{,0}}). \\ \end{gathered} $

Следуя теореме Боджно, сформулируем две граничные задачи в первом квадранте для уравнений с операторами ${{D}_{1}}$ и ${{D}_{2}}$. Ниже за каждым из уравнений следуют граничные условия, описываемые произвольными функциями:

$\begin{gathered} {{D}_{1}}{{\psi }_{1}}\left( {{{x}_{1}},{{x}_{2}}} \right) = 0,\quad {{\psi }_{1}}\left( {0,{{x}_{2}}} \right),\quad {{\psi }_{1}}\left( {{{x}_{1}},0} \right), \\ {{D}_{2}}{{\psi }_{2}}\left( {{{x}_{1}},{{x}_{2}}} \right) = 0,\quad {{\psi }_{2}}\left( {0,{{x}_{2}}} \right),\quad {{\psi }_{2}}\left( {{{x}_{1}},0} \right). \\ \end{gathered} $

Решения этих граничных задач можно представить в форме упакованных блочных элементов, имеющих вид [1]

(6)
$\begin{gathered} {{\psi }_{k}}\left( {{{x}_{1}},{{x}_{2}}} \right) = \frac{1}{{4{{\pi }^{2}}}}\iint\limits_{{{R}^{2}}} {\frac{{{{\omega }_{k}}\left( {{{\alpha }_{1}},{{\alpha }_{2}}} \right)}}{{(\alpha _{1}^{2} + \alpha _{2}^{2} - p_{k}^{2})}}} \times \\ \times \;{{e}^{{ - i\left( {{{\alpha }_{1}}{{x}_{1}} + {{\alpha }_{2}}{{x}_{2}}} \right)}}}id{{\alpha }_{1}}d{{\alpha }_{2}}, \\ {{\omega }_{k}}\left( {{{\alpha }_{1}},{{\alpha }_{2}}} \right) = \left\langle {\left[ {{{\Psi }_{k}}({{\alpha }_{{1k + }}},0) - {{\Psi }_{k}}({{\alpha }_{1}},0)} \right]} \right.({{\alpha }_{2}} - {{\alpha }_{{2k + }}}) + \\ + \;\left. {\left[ {{{\Psi }_{k}}(0,{{\alpha }_{{2k + }}}) - {{\Psi }_{k}}(0,{{\alpha }_{2}})} \right]({{\alpha }_{1}} - {{\alpha }_{{1k + }}})} \right\rangle . \\ \end{gathered} $

Здесь приняты обозначения

$\begin{gathered} {{\alpha }_{{11 + }}} = i\sqrt {\alpha _{2}^{2} - {{p}_{1}}^{2}} ,\quad {{\alpha }_{{21 + }}} = i\sqrt {\alpha _{1}^{2} - {{p}_{1}}^{2}} , \\ {{\alpha }_{{12 + }}} = i\sqrt {\alpha _{2}^{2} - {{p}_{2}}^{2}} ,\quad {{\alpha }_{{22 + }}} = i\sqrt {\alpha _{1}^{2} - {{p}_{2}}^{2},} \\ w({{x}_{1}},0) = {{\psi }_{k}}({{x}_{1}},0)\quad w(0,{{x}_{2}}) = {{\psi }_{k}}(0,{{x}_{2}}), \\ {{\Psi }_{k}}({{\alpha }_{1}},0) = \int\limits_0^\infty {{{\psi }_{k}}({{x}_{1}},0)} {{e}^{{i\left( {{{\alpha }_{1}}{{x}_{1}}} \right)}}}d{{x}_{1}}, \\ {{\Psi }_{k}}(0,{{\alpha }_{2}}) = \int\limits_0^\infty {{{\psi }_{k}}(0,{{x}_{2}})} {{e}^{{i\left( {{{\alpha }_{2}}{{x}_{2}}} \right)}}}d{{x}_{2}}. \\ \end{gathered} $

Тогда решение $\psi \left( {{{x}_{1}},{{x}_{2}}} \right)$ исходной граничной задачи будет иметь представление, разложенное по блочным элементам

$\psi \left( {{{x}_{1}},{{x}_{2}}} \right) = {{\psi }_{1}}\left( {{{x}_{1}},{{x}_{2}}} \right) + {{\psi }_{2}}\left( {{{x}_{1}},{{x}_{2}}} \right).$

Для удовлетворения граничным условиям воспользуемся координатными формулами асимптотического поведения упакованных блочных элементов вблизи их границ [12, 13]:

(7)

Используем соотношения граничных условий (5), они имеют вид

(8)
$\begin{gathered} u\left( {0,{{x}_{2}}} \right) = {{\psi }_{1}}\left( {0,{{x}_{2}}} \right) + {{\psi }_{2}}\left( {0,{{x}_{2}}} \right), \\ {{\partial }_{1}}u\left( {0,{{x}_{2}}} \right) = {{\partial }_{1}}{{\psi }_{1}}\left( {0,{{x}_{2}}} \right) + {{\partial }_{1}}{{\psi }_{2}}\left( {0,{{x}_{2}}} \right), \\ u\left( {{{x}_{1}},0} \right) = {{\psi }_{1}}\left( {{{x}_{1}},0} \right) + {{\psi }_{2}}\left( {{{x}_{1}},0} \right), \\ {{\partial }_{2}}u\left( {{{x}_{1}},0} \right) = {{\partial }_{2}}{{\psi }_{1}}\left( {{{x}_{1}},0} \right) + {{\partial }_{2}}{{\psi }_{2}}\left( {{{x}_{1}},0} \right). \\ \end{gathered} $

Применив преобразования Фурье к соотношениям (7) и (8), вычислив предельные выражения на границах области $\Omega $, получим две системы уравнений, решения которых имеют вид

$\begin{gathered} {{\Psi }_{1}}\left( {0,{{\alpha }_{2}}} \right) = \Delta _{1}^{{ - 1}}\left[ {i{{\alpha }_{{12 + }}}U(0,{{\alpha }_{2}}) - {{\partial }_{1}}U(0,{{\alpha }_{2}})} \right], \\ {{\Psi }_{2}}\left( {0,{{\alpha }_{2}}} \right) = \Delta _{1}^{{ - 1}}\left[ {{{\partial }_{1}}U(0,{{\alpha }_{2}}) - i{{\alpha }_{{11 + }}}U(0,{{\alpha }_{2}})} \right], \\ {{\Psi }_{1}}\left( {{{\alpha }_{1}},0} \right) = \Delta _{2}^{{ - 1}}\left[ {i{{\alpha }_{{22 + }}}U({{\alpha }_{1}},0) - {{\partial }_{2}}U({{\alpha }_{1}},0)} \right], \\ {{\Psi }_{2}}\left( {{{\alpha }_{1}},0} \right) = \Delta _{2}^{{ - 1}}\left[ {{{\partial }_{2}}U({{\alpha }_{1}},0) - i{{\alpha }_{{21 + }}}U({{\alpha }_{1}},0)} \right], \\ \end{gathered} $
(9)
${{\Delta }_{1}} = i{{\alpha }_{{12 + }}} - i{{\alpha }_{{11 + }}},\quad {{\Delta }_{2}} = i{{\alpha }_{{22 + }}} - i{{\alpha }_{{21 + }}},$
$\begin{gathered} U({{\alpha }_{1}},0) = \int\limits_0^\infty {u({{x}_{1}},0)} {{e}^{{i\left( {{{\alpha }_{1}}{{x}_{1}}} \right)}}}d{{x}_{1}}, \\ {{\partial }_{2}}U({{\alpha }_{1}},0) = \int\limits_0^\infty {{{\partial }_{2}}} u({{x}_{1}},0){{e}^{{i\left( {{{\alpha }_{1}}{{x}_{1}}} \right)}}}d{{x}_{1}}, \\ U(0,{{\alpha }_{2}}) = \int\limits_0^\infty u (0,{{x}_{2}}){{e}^{{i\left( {{{\alpha }_{2}}{{x}_{2}}} \right)}}}d{{x}_{2}}, \\ {{\partial }_{1}}U(0,{{\alpha }_{2}}) = \int\limits_0^\infty {{{\partial }_{1}}} u(0,{{x}_{2}}){{e}^{{i\left( {{{\alpha }_{2}}{{x}_{2}}} \right)}}}d{{x}_{2}}. \\ \end{gathered} $

Найденные значения вносятся в выражение для $\psi \left( {{{x}_{1}},{{x}_{2}}} \right)$, во внешние формы (6) и дают точное решение граничной задачи для уравнения (4) с граничными условиями (5). Несложно убедиться, используя формулы (6), (7), что построенное решение $\psi \left( {{{x}_{1}},{{x}_{2}}} \right)$ при ${{x}_{1}} \to 0$ и ${{x}_{2}} \to 0$ удовлетворяет заданным граничным условиям (5).

3. Для иллюстрации применения метода произведем вычисления для случая

$\begin{gathered} u({{x}_{1}},0) = {{H}_{1}}{{e}^{{ - {{h}_{1}}{{x}_{1}}}}},\quad {{\partial }_{2}}u({{x}_{1}},0) = {{H}_{2}}{{e}^{{ - {{h}_{2}}{{x}_{1}}}}}, \\ u(0,{{x}_{2}}) = {{G}_{1}}{{e}^{{ - {{g}_{1}}{{x}_{2}}}}},\quad {{\partial }_{1}}u(0,{{x}_{2}}) = {{G}_{2}}{{e}^{{ - {{g}_{2}}{{x}_{2}}}}}, \\ {{h}_{k}} > 0,\quad {{g}_{k}} > 0,\quad k = 1,\,2. \\ \end{gathered} $

Здесь ${{H}_{k}}$, ${{G}_{k}}$ – постоянные. В соответствии с построенными формулами (9) имеем после вычисления интегралов

$\begin{gathered} U({{\alpha }_{1}},0) = \frac{{i{{H}_{1}}}}{{{{\alpha }_{1}} + i{{h}_{1}}}},\quad {{\partial }_{2}}U({{\alpha }_{1}},0) = \frac{{i{{H}_{2}}}}{{{{\alpha }_{1}} + i{{h}_{2}}}}, \\ U(0,{{\alpha }_{2}}) = \frac{{i{{G}_{1}}}}{{{{\alpha }_{2}} + i{{g}_{1}}}},\quad {{\partial }_{1}}U(0,{{\alpha }_{2}}) = \frac{{i{{G}_{2}}}}{{{{\alpha }_{2}} + i{{g}_{2}}}}. \\ \end{gathered} $

В результате получаем формулы (9) в виде

$\begin{gathered} {{\Psi }_{1}}\left( {0,{{\alpha }_{2}}} \right) = \frac{1}{{i{{{{\alpha }}}_{{{\text{12 + }}}}} - i{{{{\alpha }}}_{{{\text{11 + }}}}}}} \times \\ \\ \times \;\left[ {i{{{{\alpha }}}_{{{\text{12 + }}}}}\frac{{i{{G}_{1}}}}{{{{\alpha }_{2}} + i{{g}_{1}}}} - \frac{{i{{G}_{2}}}}{{{{\alpha }_{2}} + i{{g}_{2}}}}} \right], \\ \\ {{\Psi }_{2}}\left( {0,{{\alpha }_{2}}} \right) = \frac{1}{{i{{{{\alpha }}}_{{{\text{12 + }}}}} - i{{{{\alpha }}}_{{{\text{11 + }}}}}}} \times \\ \\ \times \;\left[ { - i{{{{\alpha }}}_{{{\text{11 + }}}}}\frac{{i{{G}_{1}}}}{{{{\alpha }_{2}} + i{{g}_{1}}}} + \frac{{i{{G}_{2}}}}{{{{\alpha }_{2}} + i{{g}_{2}}}}} \right], \\ \end{gathered} $
$\begin{gathered} {{\Psi }_{1}}\left( {{{\alpha }_{1}},0} \right) = \frac{1}{{i{{{{\alpha }}}_{{{\text{22 + }}}}} - i{{{{\alpha }}}_{{{\text{21 + }}}}}}} \times \\ \\ \times \;\left[ {i{{{{\alpha }}}_{{{\text{22 + }}}}}\frac{{i{{H}_{1}}}}{{{{\alpha }_{1}} + i{{h}_{1}}}} - \frac{{i{{H}_{2}}}}{{{{\alpha }_{1}} + i{{h}_{2}}}}} \right], \\ \\ {{\Psi }_{2}}\left( {{{\alpha }_{1}},0} \right) = \frac{1}{{i{{{{\alpha }}}_{{{\text{22 + }}}}} - i{{{{\alpha }}}_{{{\text{21 + }}}}}}} \times \\ \\ \times \;\left[ { - i{{{{\alpha }}}_{{{\text{21 + }}}}}\frac{{i{{H}_{1}}}}{{{{\alpha }_{1}} + i{{h}_{1}}}} + \frac{{i{{H}_{2}}}}{{{{\alpha }_{1}} + i{{h}_{2}}}}} \right]. \\ \end{gathered} $

Нормализовав обобщенные функции и вычислив обращения Фурье, будем иметь выражения для граничных условий блочных элементов посредством заданных граничных условий в виде классических функций

$\begin{gathered} {{\psi }_{1}}\left( {0,{{x}_{2}}} \right) = \left( { - \frac{{{{\partial }^{2}}}}{{\partial x_{2}^{2}}} + {{p}^{2}}} \right) \times \\ \times \;\frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\frac{{{{\Psi }_{1}}\left( {0,{{\alpha }_{2}}} \right)}}{{(\alpha _{2}^{2} + {{p}^{2}})}}} {{e}^{{ - i{{\alpha }_{2}}{{x}_{2}}}}}d{{\alpha }_{2}} = \\ = \;\left( { - \frac{{{{\partial }^{2}}}}{{\partial x_{2}^{2}}} + {{p}^{2}}} \right)\frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\frac{1}{{(\alpha _{2}^{2} + {{p}^{2}})(i{{{{\alpha }}}_{{{\text{12 + }}}}} - i{{{{\alpha }}}_{{{\text{11 + }}}}})}}} \times \\ \times \;\left[ {i{{{{\alpha }}}_{{{\text{12 + }}}}}\frac{{i{{G}_{1}}}}{{{{\alpha }_{2}} + i{{g}_{1}}}} - \frac{{i{{G}_{2}}}}{{{{\alpha }_{2}} + i{{g}_{2}}}}} \right]{{e}^{{ - i{{\alpha }_{2}}{{x}_{2}}}}}d{{\alpha }_{2}}, \\ \end{gathered} $
$\begin{gathered} {{\psi }_{2}}\left( {0,{{x}_{2}}} \right) = \left( { - \frac{{{{\partial }^{2}}}}{{\partial x_{2}^{2}}} + {{p}^{2}}} \right) \times \\ \times \;\frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\frac{{{{\Psi }_{2}}\left( {0,{{\alpha }_{2}}} \right)}}{{(\alpha _{2}^{2} + {{p}^{2}})}}} {{e}^{{ - i{{\alpha }_{2}}{{x}_{2}}}}}d{{\alpha }_{2}} = \\ = \;\left( { - \frac{{{{\partial }^{2}}}}{{\partial x_{2}^{2}}} + {{p}^{2}}} \right)\frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\frac{1}{{(\alpha _{2}^{2} + {{p}^{2}})(i{{{{\alpha }}}_{{{\text{12 + }}}}} - i{{{{\alpha }}}_{{{\text{11 + }}}}})}}} \times \\ \times \;\left[ { - i{{{{\alpha }}}_{{{\text{11 + }}}}}\frac{{i{{G}_{1}}}}{{{{\alpha }_{2}} + i{{g}_{1}}}} + \frac{{i{{G}_{2}}}}{{{{\alpha }_{2}} + i{{g}_{2}}}}} \right]{{e}^{{ - i{{\alpha }_{2}}{{x}_{2}}}}}d{{\alpha }_{2}}, \\ \end{gathered} $
$\begin{gathered} {{\psi }_{1}}\left( {{{x}_{1}},0} \right) = \left( { - \frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + {{p}^{2}}} \right) \times \\ \\ \times \;\frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\frac{{{{\Psi }_{1}}\left( {{{\alpha }_{1}},0} \right)}}{{(\alpha _{1}^{2} + {{p}^{2}})}}} {{e}^{{ - i{{\alpha }_{1}}{{x}_{1}}}}}d{{\alpha }_{1}} = \\ \\ = \;\left( { - \frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + {{p}^{2}}} \right)\frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\frac{1}{{(\alpha _{1}^{2} + {{p}^{2}})(i{{{{\alpha }}}_{{{\text{22 + }}}}} - i{{{{\alpha }}}_{{{\text{21 + }}}}})}}} \times \\ \\ \times \;\left[ {i{{{{\alpha }}}_{{{\text{22 + }}}}}\frac{{i{{H}_{1}}}}{{{{\alpha }_{1}} + i{{h}_{1}}}} - \frac{{i{{H}_{2}}}}{{{{\alpha }_{1}} + i{{h}_{2}}}}} \right]{{e}^{{ - i{{\alpha }_{1}}{{x}_{1}}}}}d{{\alpha }_{1}}, \\ \end{gathered} $
$\begin{gathered} {{\psi }_{2}}\left( {{{x}_{1}},0} \right) = \left( { - \frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + {{p}^{2}}} \right) \times \\ \\ \times \;\frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\frac{{{{\Psi }_{2}}\left( {{{\alpha }_{1}},0} \right)}}{{(\alpha _{1}^{2} + {{p}^{2}})}}} {{e}^{{ - i{{\alpha }_{1}}{{x}_{1}}}}}d{{\alpha }_{1}} = \\ \\ = \;\left( { - \frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + {{p}^{2}}} \right)\frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\frac{1}{{(\alpha _{1}^{2} + {{p}^{2}})(i{{{{\alpha }}}_{{{\text{22 + }}}}} - i{{{{\alpha }}}_{{{\text{21 + }}}}})}}} \times \\ \\ \times \;\left[ { - i{{{{\alpha }}}_{{{\text{21 + }}}}}\frac{{i{{H}_{1}}}}{{{{\alpha }_{1}} + i{{h}_{1}}}} + \frac{{i{{H}_{2}}}}{{{{\alpha }_{1}} + i{{h}_{2}}}}} \right]{{e}^{{ - i{{\alpha }_{1}}{{x}_{1}}}}}d{{\alpha }_{1}}. \\ \end{gathered} $

Легко видеть, что

$\begin{gathered} {{\psi }_{1}}\left( {0,{{x}_{2}}} \right) + {{\psi }_{2}}\left( {0,{{x}_{2}}} \right) = \left( { - \frac{{{{\partial }^{2}}}}{{\partial x_{2}^{2}}} + {{p}^{2}}} \right) \times \\ \times \;\frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\frac{{i{{G}_{1}}}}{{(\alpha _{2}^{2} + {{p}^{2}})({{\alpha }_{2}} + i{{g}_{1}})}}} {{e}^{{ - i{{\alpha }_{2}}{{x}_{2}}}}}d{{\alpha }_{2}} = {{G}_{1}}{{e}^{{ - {{g}_{1}}{{x}_{2}}}}}, \\ \\ {{\psi }_{1}}\left( {{{x}_{1}},0} \right) + {{\psi }_{2}}\left( {{{x}_{1}},0} \right) = \left( { - \frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + {{p}^{2}}} \right) \times \\ \times \;\frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\frac{{i{{H}_{1}}}}{{(\alpha _{1}^{2} + {{p}^{2}})({{\alpha }_{1}} + i{{h}_{1}})}}} {{e}^{{ - i{{\alpha }_{1}}{{x}_{1}}}}}d{{\alpha }_{1}} = {{H}_{1}}{{e}^{{ - {{h}_{1}}{{x}_{1}}}}}. \\ \end{gathered} $

Для проверки условий

$\begin{gathered} {{\partial }_{1}}{{\psi }_{1}}\left( {0,{{x}_{2}}} \right) + {{\partial }_{1}}{{\psi }_{2}}\left( {0,{{x}_{2}}} \right) = {{G}_{2}}{{e}^{{ - {{g}_{2}}{{x}_{2}}}}}, \\ {{\partial }_{2}}{{\psi }_{1}}\left( {{{x}_{1}},0} \right) + {{\partial }_{2}}{{\psi }_{2}}\left( {{{x}_{1}},0} \right) = {{H}_{2}}{{e}^{{ - {{h}_{2}}{{x}_{1}}}}} \\ \end{gathered} $
нужно воспользоваться представлениями (7), для вычисления под интегралом производных, а затем выполнить проверку, как и выше.

Появление обобщенных функций при задании в граничных условиях компонент производных связано с возникновением, в этом случае, сингулярных концентраций напряжений в угловой точке для уравнений Ламе, которые блочные элементы также должны описывать.

ВЫВОД

В работе [15] показано, что множество блочных элементов, граничных задач для уравнения Гельмгольца, порождает дискретное топологическое пространство. Результаты настоящей работы показывают, что множество граничных задач, порождаемых уравнениями Гельмгольца, гомеоморфизмом индуцируют дискретное топологическое пространство уже для граничных задач сложной реологии, к системам уравнений которых применимо преобразование Галёркина. Таким образом, изменением топологий пространств, дроблением или объединением носителей, остающихся дискретными пространствами, можно получать решения граничных задач для систем дифференциальных уравнений с постоянными коэффициентами в сложных неклассических областях.

Список литературы

  1. Бабешко В.А., Евдокимова О.В., Бабешко О.М. Метод блочного элемента в разложении решений сложных граничных задач механики // ДАН. 2020. Т. 495. С. 34–38. https://doi.org/10.31857/S2686740020060048

  2. Galerkin B.G. Contribution a la solution generale du probleme de la theorie de lelastisitecas de troisdimensions // C.R. Acad. Sci. 1930. V. 190. P. 1047–1048; 1931. V. 193. P. 568–571.

  3. Новацкий В. Теория упругости. М.: Мир, 1975. 872 с.

  4. Новацкий В. Динамические задачи термоупругости. М.: Мир, 1970. 256 с.

  5. Новацкий В. Электромагнитные эффекты в твердых телах. М.: Мир, 1986. 162 с.

  6. Улитко А.Ф. Метод собственных векторных функций в пространственных задачах теории упругости. Киев: Наук. думка, 1979. 262 с.

  7. Головчан В.Т., Кубенко В.Д., Шульга Н.А., Гуз А.Н., Гринченко В.Т. Динамика упругих тел. Киев: Наук. думка, 1986. 288 с.

  8. Гельфанд И.М., Минлос З.А., Шапиро З.Я. Представления группы вращений и группы Лоренца, их применения. М.: Физматлит, 1958. 368 с.

  9. Babeshko V.A., Evdokimova O.V., Babeshko O.M. On the possibility of predicting some types of earthquake by a mechanical approach // Acta Mechanica. 2018. V. 229. № 5. P. 2163–2175.

  10. Babeshko V.A., Evdokimova O.V., Babeshko O.M. On a mechanical approach to the prediction of earthquakes during horizontal motion of litospheric plates // Acta Mechanica. 2018. V. 229. № 11. P. 4727–4739.

  11. Babeshko V.A., Evdokimova O.V., Babeshko O.M. About earthquakes in subduction zones with the potential to cause a tsunami // J. Appllied and Computational Mechanics. 2020. https://doi.org/10.22055/JACM

  12. Бабешко В.А., Евдокимова О.В., Бабешко О.М. Об одном методе решения граничных задач динамической теории упругости в четверть плоскости // ПММ. 2021. № 3 (в печати).

  13. Бабешко В.А., Евдокимова О.В., Бабешко О.М. О разложении решений скалярных граничных задач по блочным элементам // МТТ. 2021. Т. 85. № 3. С. 275–282. https://doi.org/10.31857/S0032823521030024

  14. Boggio T. Sull integrazioedi alcuno equatoini linerary alle derivate parziale //Ann. Mat. Ser. III. 1903. V. 8. P. 181.

  15. Бабешко В.А., Евдокимова О.В., Бабешко О.М., Бушуева О.А. Топологическая дискретизация решений граничных задач механики сплошной среды // Экологический вестник научных центров Черноморского экономического сотрудничества. 2020. Т. 16. № 3. С. 65–71. https://doi.org/10.31429/vestnik-17-3-65-71

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал