Доклады Российской академии наук. Физика, технические науки, 2021, T. 498, № 1, стр. 40-45

АНАЛИТИЧЕСКИЕ ОЦЕНКИ ДВИЖЕНИЯ И УПРУГИХ КОЛЕБАНИЙ КОНСТРУКЦИЙ ОТДЕЛЯЕМЫХ СТВОРОК ОБТЕКАТЕЛЕЙ РАКЕТНО-КОСМИЧЕСКИХ СИСТЕМ

В. Н. Бакулин^1, *, С. В. Борзых^2, **

¹ Институт прикладной механики Российской академии наук
Москва, Россия

² ПАО РКК “Энергия” им. С.П. Королева
Московская область, Королев, Россия

^* E-mail: vbak@yandex.ru
^** E-mail: rigidbor@gmail.com

Поступила в редакцию 29.03.2021
После доработки 29.03.2021
Принята к публикации 02.04.2021

DOI: 10.31857/S2686740021030044

Полный текст (PDF)

Аннотация

Получены уравнения и построена модель для исследования динамики процесса отделения створок обтекателей ракетно-космических систем. На основе предположения о малости угловой скорости вращения створок в процессе отделения по сравнению с низшими частотами их собственных колебаний получены две независимые группы аналитических соотношений, одна из которых описывает пространственное движение створок как целого относительно ракеты-носителя, а вторая – упругие колебания на участке разворота относительно осей, зафиксированных на носителе. На основании полученных соотношений первой группы строятся траектории движения створок в процессе отделения. Во второй группе уравнений исследованы зависимости уровня возбуждения колебаний створок от разновременности включения двигателей отделения и/или разброса характеристик толкателей.

Ключевые слова: ракета-носитель, створки обтекателя, процесс отделения, колебания

ПОСТАНОВКА ЗАДАЧИ

Некоторые вопросы моделирования динамики элементов ракетно-космических систем (РКС) по тематике представленной статьи рассматривались, например, в работах [1–4]. Процессы механической трансформации РКС, сопровождающиеся изменением их структуры и/или конфигурации – критически важные операции, отказ или нештатное функционирование которых практически всегда означает невыполнение задач миссии [5–8].

Отделение отработавших элементов ракетно-космических систем – характерный пример такого рода процессов, поэтому к обеспечению безопасности отделения и обоснованности выбора характеристик средств отделения (СО) предъявляются высокие требования. В то же время при наземной экспериментальной отработке не удается воспроизвести реальные полетные условия. Поэтому основным средством подтверждения правильности принятых технических решений является математическое моделирование с максимальным учетом характерных особенностей процессов отделения [9–12].

Одним из наиболее ответственных является процесс отделения защитных створок обтекателей полезного груза. Обтекатель предназначен для защиты аппарата от ветра, пыли на стартовом столе, от интенсивных нагрузок (акустических, тепловых и т.д.) на участке выведения. После прохождения атмосферного участка его защитная функция перестает быть необходимой, и он отделяется от ракеты-носителя. Обтекатель включает несколько раздельно сбрасываемых створок (рис. 1). В первой фазе отделения для обеспечения организованного движения створки разворачиваются относительно осей вращения, размещенных на носителе. Затем, после достижения определенного угла разворота, связь с носителем разрывается, и начинается участок автономного движения створки.

Рис. 1.

Относительное движение створок и ракеты-носителя.

Конструктивно обтекатель представляет собой, как правило, комбинацию оболочек вращения – цилиндров, конусов, сфер. Под ним с некоторым зазором находится зона конструкции космического аппарата. Величина зазора определяется в основном амплитудой упругих колебаний створок обтекателя в процессе отделения. Недостаточный зазор может привести к соударению створок с конструкцией аппарата и вызвать повреждения.

Избыточно большой зазор (“везем воздух”) увеличивает диаметр обтекателя, что влечет за собой увеличение веса, аэродинамического сопротивления, нагрузок на конструкцию.

Створки обладают большими массами и моментами инерции относительно осей вращения. Разворот створок происходят под действием значительных сосредоточенных сил, создаваемых специальными средствами отделения, установленными в нескольких точках конструкции. Существующие подходы к расчету динамики отделения обтекателей обычно базировались на моделях створок как абсолютно твердых тел [1]. В такой постановке определялось движение отделившихся створок относителя, чтобы убедиться в отсутствии соударений с ним в дальнейшем относительном движении. Скорость створок после срабатывания средств отделения и траектории относительного движения хорошо согласовывались с твердой моделью, а достаточность необходимой величины зазора, определяемой уровнем колебаний, подтверждалась на наземных экспериментальных установках для отработки процесса отделения. Для оптимального выбора требуемой величины зазора уже на этапе предварительного проектирования требуется прогнозный расчет уровня упругих колебаний створок при отделении.

В самой общей постановке изучение отделения и направленного перемещения упругих конструкций является сложной задачей, так как такие движения описываются громоздкими “гибридными” системами, включающими как уравнения в частных производных, так и обыкновенные дифференциальные уравнения [13]. Исходя из конструктивных особенностей разделяемых тел и опыта технической реализации процессов разделения можно сделать предположение о малости упругих деформаций по сравнению с характерными линейными размерами створок, которые могут достигать нескольких десятков метров. Таким образом, задача об упругих деформациях может решаться в линейной постановке. Поэтому представляется целесообразным подход, использующий разложение движения упругого тела на естественные составляющие: движение створки как твердого тела (описываемое в общем случае нелинейными уравнениями) и малые линейные упругие колебания около порождающего движения, представленные в модальном виде, т.е. в виде разложения по собственным формам колебаний, методы определения которых описаны, например, в [14]. В практических расчетах может использоваться конечное число низших форм, так как частотный спектр створок, как правило, разряженный, и вклад каждой частной формы в общую деформацию быстро падает с увеличением номера формы.

Как отмечалось выше, “твердые” модели достаточно точно позволяют рассчитывать относительное движение носителя и створок после их отделения, что является отражением того факта, что силы инерции, обусловленные движением створок как целого, практически не влияют на их колебательное движение. В связи с этим уравнения движения как целого (по твердым формам) и малые упругие колебания можно анализировать независимо.

ДВИЖЕНИЯ СТВОРОК КАК ТВЕРДОГО ЦЕЛОГО ОТНОСИТЕЛЬНО РАКЕТЫ-НОСИТЕЛЯ

Анализ безопасности отделения створок базируется на изучении траекторий и скоростей относительного движения створок как твердого целого и носителя (рис. 1).

Для каждого тела системы записываются законы изменения количества движения и кинетического момента:

(1)

${{m}_{i}}\frac{{{{d}^{2}}{{r}_{{0i}}}}}{{d{{t}^{2}}}} = \sum {F_{i}^{{\left( e \right)}}} ,$

(2)

$\left[ {{{I}_{{0i}}}} \right]\frac{{{{\omega }_{i}}}}{{dt}} + {{\omega }_{i}} \times \left( {\left[ {{{I}_{{0i}}}} \right]{{\omega }_{i}}} \right) = \sum {{{M}_{{0i}}}({{F}^{{\left( e \right)}}})} ,$

где m_i, $\left[ {{{I}_{{0i}}}} \right]$, ${{\omega }_{i}}$, $\sum {F_{i}^{{\left( e \right)}}} $, $\sum {{{M}_{{0i}}}} ({{F}^{{\left( e \right)}}})$ – массы, тензоры инерции, угловые скорости, главные вектора и главные моменты внешних сил ракеты-носителя и створок обтекателя.

Ниже приведены аналитические кинематические соотношения, позволяющие определить радиусы-векторы скорости и ускорения центров масс створок в системе координат ракеты-носителя:

$r_{{{{0}_{2}}}}^{{отн}} = \left[ {{{M}_{{ин \to 1}}}} \right]\left( {{{r}_{{{{0}_{2}}}}} - {{r}_{{{{0}_{1}}}}}} \right),$

(3)

$\begin{gathered} \tilde {V}_{{{{0}_{2}}}}^{{отн}} = \left[ {{{M}_{{ин \to 1}}}} \right]\left( {\frac{{d{{r}_{{{{0}_{2}}}}}}}{{dt}} - \frac{{d{{r}_{{{{0}_{1}}}}}}}{{dt}}} \right) - {{\omega }_{1}} \times \\ \times \;\left[ {{{M}_{{ин \to 1}}}} \right]\left( {{{r}_{{{{0}_{2}}}}} - {{r}_{{{{0}_{1}}}}}} \right), \\ \end{gathered} $

$\begin{gathered} \tilde {a}_{{{{0}_{2}}}}^{{отн}} = \left[ {{{M}_{{ин \to 1}}}} \right]\left( {\frac{{{{d}^{2}}{{r}_{{{{0}_{2}}}}}}}{{d{{t}^{2}}}} - \frac{{{{d}^{2}}{{r}_{{{{0}_{1}}}}}}}{{d{{t}^{2}}}}} \right) - \\ - \;{{\varepsilon }_{1}} \times \left[ {{{M}_{{ин \to 1}}}} \right]\left( {{{r}_{{{{0}_{2}}}}} - {{r}_{{{{0}_{1}}}}}} \right) - \\ - \;{{\omega }_{1}} \times \left\{ {\tilde {V}_{{{{0}_{2}}}}^{{отн}}\left[ {{{M}_{{ин \to 1}}}} \right]\left( {\frac{{{{d}^{2}}{{r}_{{{{0}_{2}}}}}}}{{d{{t}^{2}}}} - \frac{{{{d}^{2}}{{r}_{{{{0}_{1}}}}}}}{{d{{t}^{2}}}}} \right)} \right\}. \\ \end{gathered} $

Аналогичные параметры некоторой характерной “опасной” (в смысле возможного соударения с ракетой-носителем) точки конструкции створок определяются зависимостями

$r_{i}^{{отн}} = \left[ {{{M}_{{ин \to 1}}}} \right]\left( {{{r}_{{{{0}_{2}}}}} - {{r}_{{{{0}_{1}}}}}} \right) + \left[ {{{M}_{{2 \to 1}}}} \right]{{r}_{i}},$

$\begin{gathered} \tilde {V}_{i}^{{отн}} = \left[ {{{M}_{{ин \to 1}}}} \right]\left( {\frac{{d{{r}_{{{{0}_{2}}}}}}}{{dt}} - \frac{{d{{r}_{{{{0}_{1}}}}}}}{{dt}}} \right) + \left[ {{{M}_{{2 \to 1}}}} \right]\left( {{{\omega }_{2}} \times {{r}_{i}}} \right) - \\ - \;{{\omega }_{1}} \times \left\{ {\left[ {{{M}_{{ин \to 1}}}} \right]\left( {{{r}_{{{{0}_{2}}}}} - {{r}_{{{{0}_{1}}}}}} \right) + \left[ {{{M}_{{2 \to 1}}}} \right]{{r}_{i}}} \right\}, \\ \end{gathered} $

$\begin{gathered} \tilde {a}_{i}^{{отн}} = \left[ {{{M}_{{ин \to 1}}}} \right]\left( {\frac{{{{d}^{2}}{{r}_{{{{0}_{2}}}}}}}{{d{{t}^{2}}}} - \frac{{{{d}^{2}}{{r}_{{{{0}_{1}}}}}}}{{d{{t}^{2}}}}} \right) + \\ + \;\left[ {{{M}_{{2 \to 1}}}} \right]\left\{ {{{\varepsilon }_{2}} \times {{r}_{i}} + {{\omega }_{2}} \times \left( {{{\omega }_{2}} \times {{r}_{i}}} \right)} \right\} - \\ - \;{{\varepsilon }_{1}} \times {{r}_{i}}^{{отн}} - {{\omega }_{1}} \times ({{\omega }_{1}} \times r_{i}^{{отн}}) - 2{{\omega }_{1}} \times \tilde {V}_{i}^{{отн}}. \\ \end{gathered} $

Входящие в приведенные выше соотношения матрицы перехода между системами координат находятся традиционными способами [1, 13].

Движение створки относительно носителя может быть сразу описано в его подвижной системе координат:

${{m}_{2}}\frac{{{{d}^{2}}r_{{{{0}_{2}}}}^{{отн}}}}{{d{{t}^{2}}}} = \sum {F_{2}^{{\left( e \right)}} + {{Ф}_{{{{2}_{e}}}}} + {{Ф}_{{кор}}}} ,$

где силы инерции переносного движения и силы инерции Кориолиса определяются следующим образом:

${{Ф}_{{{{2}_{e}}}}} = - {{m}_{2}}[{{\omega }_{2}} \times ({{\omega }_{2}} \times r_{{{{0}_{2}}}}^{{отн}}) + {{\varepsilon }_{2}} \times r_{{{{0}_{2}}}}^{{отн}}],$

${{Ф}_{{кор}}} = - {{m}_{2}}{{a}_{{{{2}_{{кор}}}}}} = - 2{{m}_{2}}{{\omega }_{2}} \times \tilde {V}_{{{{0}_{2}}}}^{{отн}}.$

Векторы $r_{{{{0}_{2}}}}^{{отн}}$ и $\tilde {V}_{{{{0}_{2}}}}^{{отн}}$ определяются выражениями (3).

Процесс отделения створок считается безопасным при отсутствии соударений любой точки конструкции створок с носителем в их относительном движении.

УПРУГИЕ КОЛЕБАНИЯ КОНСТРУКЦИИ СТВОРОК

Интенсивные колебания створок возникают под действием сил, создаваемых специальными средствами отделения – толкателями (пружинными, пиротехническими, пневматическими), твердотопливными двигателями. Малые упругие колебания могут быть представлены в модальном виде, т.е. в виде разложения в ряд по собственным формам колебаний [14, 15]. Предполагается, что выполняется свойство ортогональности форм и вклад каждой частной формы в общую деформацию не зависит от вклада по другим формам.

Тогда отдельные уравнения по каждому тону колебаний (элементарного осциллятора)

${{\ddot {S}}_{n}} + \omega _{n}^{2}{{S}_{n}} = \sum\limits_i^{} {[F_{i}^{x}f_{{ni}}^{x} + F_{i}^{y}f_{{ni}}^{z}f_{{ni}}^{z}]} $

будут независимы, и в этом случае они решаются аналитически:

(4)

$\begin{gathered} {{S}_{n}}\left( t \right) = {{S}_{{n0}}}\cos {{\omega }_{n}}t + \frac{{{{{\dot {S}}}_{{n0}}}}}{{{{\omega }_{n}}}}\sin {{\omega }_{n}}t + \\ + \frac{1}{{{{\omega }_{n}}}}\int\limits_0^t {\sum\limits_i^{} {[F_{i}^{x}f_{{ni}}^{x} + F_{i}^{y}f_{{ni}}^{y} + F_{i}^{z}f_{{ni}}^{z}]} \sin {{\omega }_{n}}\left( {t - \tau } \right)d} \tau , \\ \end{gathered} $

где ${{S}_{{n0}}}$, ${{\dot {S}}_{{n0}}}$ – начальные условия, ${{F}_{i}}$ – компоненты силы i-го средства отделения, а формы f_ni ортонормированы.

Силы в правых частях уравнения (4) создаются, как правило, либо толкателями, либо твердотопливными ракетными двигателями (РДТТ). Зависимость тяги РДТТ от времени близка к постоянной. То же самое можно сказать и об изменении силы толкателей, особенно в начальной, наиболее опасной фазе процесса отделения. Тогда в (4) проекции сил могут быть вынесены из-под знака интеграла.

С точки зрения уменьшения возмущений при разделении и снижения нагрузок на узлы связи предпочтительными являются симметричные схемы процесса, когда плоскость отделения совпадает с плоскостью симметрии отделяемой конструкции, при этом средства отделения установлены попарно симметрично [1, 2]. Отделение створок обтекателей выполнено именно по такой схеме (рис. 2).

Рис. 2.

Схема расположения средств отделения створок.

Пусть для нее $F_{1}^{x} = F_{2}^{x}$; $F_{1}^{y} = F_{2}^{y}$; $F_{1}^{z} = F_{2}^{z}$ (ось x продольная). Тогда $f_{{n1}}^{x} = f_{{n2}}^{x}$; $f_{{n1}}^{y} = - f_{{n2}}^{y}$; $f_{{n1}}^{z} = f_{{n2}}^{z}$ для симметричных форм и $f_{{n1}}^{x} = - f_{{n2}}^{x}$; $f_{{n1}}^{y} = f_{{n2}}^{y}$; $f_{{n1}}^{z} = - f_{{n2}}^{z}$ для кососимметричных.

РДТТ могут иметь задержку включения по времени друг относительно друга. Возможен также разброс сил, развиваемых отдельными толкателями. Из (4) видно, что кососимметричные формы будут возбуждаться только при наличии задержки Δt включения одного из РДТТ (или разнице сил толкателей), иначе возбуждение охватывает только симметричные формы. В этом случае при Δt = 0 для симметричных форм в период действия силы из (4) получим

(5)

$\begin{gathered} {{S}_{n}}\left( t \right) = \frac{{2[F_{1}^{x}U_{{n1}}^{x} + F_{1}^{y}U_{{n1}}^{y} + F_{1}^{z}U_{{n1}}^{z}]}}{{\omega _{n}^{2}}}{{\psi }_{n}}\left( t \right); \\ {{\psi }_{n}}\left( t \right) = \left\{ \begin{gathered} 0,\quad t \leqslant 0, \hfill \\ 1 - \cos {{\omega }_{n}}t,\quad 0 < t \leqslant T, \hfill \\ \cos {{\omega }_{n}}\left( {t - T} \right) - \cos {{\omega }_{n}}t,\quad t \geqslant T, \hfill \\ \end{gathered} \right. \\ \end{gathered} $

где $T$ – время работы РДТТ. В период работы РДТТ колебания происходят около смещенного положения:

(6)

${{S}_{n}} = \frac{{2[F_{1}^{x}f_{{n1}}^{x} + F_{1}^{y}f_{{n1}}^{y} + F_{1}^{z}f_{{n1}}^{z}]}}{{\omega _{n}^{2}}},$

а после окончания работы средств отделения сохраняются остаточные колебания около нулевого значения S_n = 0 (рис. 3).

Рис. 3.

Характер колебательного процесса при отсутствии задержки включения.

Упругая деформация в произвольной точке створки

(7)

$\left\{ \begin{gathered} u_{i}^{x} \hfill \\ u_{i}^{y} \hfill \\ u_{i}^{z} \hfill \\ \end{gathered} \right\} = \sum\limits_{n = 1}^{{{n}_{k}}} {{{S}_{n}}\left( t \right)\left\{ \begin{gathered} U_{{ni}}^{x} \hfill \\ U_{{ni}}^{y} \hfill \\ U_{{ni}}^{z} \hfill \\ \end{gathered} \right\},} $

где $U_{{ni}}^{x}$, $U_{{ni}}^{y}$, $U_{{ni}}^{z}$ – компоненты вектора собственных форм в этой точке, а суммирование ведется только по симметричным формам.

Поскольку вклад в упругую деформацию высших форм быстро падает с ростом номера формы, в реальных расчетах учитывается ограниченное их число. Максимальное значение упругой деформации, как видно из рис. 2, получается удвоением (6).

Рассмотрим влияние задержки включения одного из двигателей на характер процесса. Предположим, что задержка включения $\Delta t$ заметно меньше времени работы двигателя: $t \ll T$, что имеет место в действительности. Тогда для симметричных форм в течение работы двигателя $\Delta t < t < T$, интегрируя (4), получим

(8)

$\begin{gathered} {{S}_{n}}\left( t \right) = \frac{{2[F_{1}^{x}U_{{n1}}^{x} + F_{1}^{y}U_{{n1}}^{y} + F_{1}^{z}U_{{n1}}^{z}]}}{{\omega _{n}^{2}}} \times \\ \times \;\left[ {1 - \cos \left( {{{\omega }_{n}}\frac{{\Delta t}}{2}} \right)\cos {{\omega }_{n}}\left( {t - \frac{{\Delta t}}{2}} \right)} \right]; \\ \end{gathered} $

для кососимметричных форм

(9)

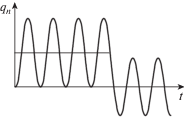
$\begin{gathered} {{S}_{n}}\left( t \right) = \frac{{2[F_{1}^{x}U_{{n1}}^{x} + F_{1}^{y}U_{{n1}}^{y} + F_{1}^{z}U_{{n1}}^{z}]}}{{\omega _{n}^{2}}} \times \\ \times \;\sin \left( {{{\omega }_{n}}\frac{{\Delta t}}{2}} \right)\sin {{\omega }_{n}}\left( {t - \frac{{\Delta t}}{2}} \right). \\ \end{gathered} $

Выражение (8), так же как и (5), описывает колебания около смещенного положения, определяемого соотношением (6). Однако, в отличие от (5), амплитуда этих колебаний зависит от времени задержки $\Delta t$. Амплитуда максимальна и равна амплитуде колебаний (5), когда время задержки кратно периоду колебаний на данной частоте Δt = = $\frac{{2\pi a}}{{{{\omega }_{n}}}}$. Если время задержки отличается от кратного на полпериода $\Delta t = \frac{{2\pi a + \pi }}{{{{\omega }_{n}}}}$, колебания около среднего положения отсутствуют (рис. 4). Сохраняет силу и оценка (6) средних значений упругих деформаций, вызванных возбуждением симметричных форм колебаний, а также оценка их максимальных значений, как удвоенного значения (6).

Рис. 4.

Характер колебательного процесса для времени задержки, отличающегося от кратного на полпериода.

Оценим вклад кососимметричных форм в упругую деформацию створок. Как видно из (9), колебания на кососимметричных формах происходят около невозмущенного значения ${{q}_{n}} = 0$. При этом амплитуда колебаний зависит от времени задержки $\Delta t$. Амплитуда равна нулю, когда время задержки кратно периоду колебаний на данной частоте $\Delta t = \frac{{2\pi a}}{{{{\omega }_{n}}}}$. Амплитуда достигает максимума, когда время задержки отличается от кратного на полпериода колебаний на данной частоте $\Delta t = \frac{{2\pi a + \pi }}{{{{\omega }_{n}}}}$. Суммарный вклад кососимметричных форм оценивается рядом

(10)

$\begin{gathered} \left\{ \begin{gathered} \left| {u_{i}^{x}} \right| \hfill \\ \left| {u_{i}^{y}} \right| \hfill \\ \left| {u_{i}^{z}} \right| \hfill \\ \end{gathered} \right\} \leqslant \sum\limits_{n = 1}^{{{n}_{k}}} {2\left| {[F_{1}^{x}U_{{n1}}^{x} + F_{1}^{y}U_{{n1}}^{y}{{ + }_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}} \right.} \\ \left. { + \,F_{1}^{z}U_{{n1}}^{z}]\omega _{n}^{{ - 2}}\sin \left( {{{\omega }_{n}}\frac{{\Delta t}}{2}} \right)} \right|\left\{ \begin{gathered} \left| {U_{{ni}}^{x}} \right| \hfill \\ \left| {U_{{ni}}^{y}} \right| \hfill \\ \left| {U_{{ni}}^{z}} \right| \hfill \\ \end{gathered} \right\}, \\ \end{gathered} $

где суммирование ведется только по кососимметричным формам. При условии малости задержки включения одного из РДТТ по сравнению с периодом колебаний на низших частотах ${{\omega }_{n}}\frac{{\Delta t}}{2} \ll 1$ можно положить $\sin \left( {{{\omega }_{n}}\frac{{\Delta t}}{2}} \right)$$ \approx {{\omega }_{n}}\frac{{\Delta t}}{2}$. Таким образом, в указанных пределах возбуждение кососимметричных форм колебаний происходит тем сильнее, чем значительнее время задержки Δt, при нулевой задержке $\Delta t = 0$ кососимметричные формы вообще не возбуждаются.

ЗАКЛЮЧЕНИЕ

Введение упрощающих предположений позволило рассмотреть отдельные уравнения колебаний как независимые и получить аналитические оценки (4)–(10). Предполагалось, в частности, что колебания створок являются малыми, линейными, а угловая скорость створок в процессе их разворота как минимум на порядок меньше собственных частот колебаний даже на низших формах. Это позволило учитывать вклад в упругую деформацию только значительных по величине сил, создаваемых средствами отделения.

Список литературы

Колесников К.С., Козлов В.И., Кокушкин В.В. Разделение ступеней летательных аппаратов. М.: Машиностроение, 1977. 223 с.
Бакулин В.Н., Борзых С.В., Решетников М.Н. Моделирование относительного движения возвращаемой капсулы и транспортного корабля при их разделении // Вестник МАИ. 2011. Т. 18. № 3. С. 287–294.
Бакулин В.Н., Борзых С.В., Ильясова И.Р. Математическое моделирование процесса раскрытия многозвенных солнечных батарей // Вестник МАИ. 2011. Т. 18. № 3. С. 295–302.
Бакулин В.Н., Борзых С.В., Богомолов Н.В. Алгоритм отделения транспортного пилотируемого корабля “Союз” от нестабилизированной Международной космической станции // Известия вузов. Авиационная техника. 2019. № 4. С. 48–54.
Береговой Г.Т., Ярополов В.И., Баранецкий И.И. и др. Справочник по безопасности космических полетов. М.: Машиностроение, 1989. 336 с.
Bergez G. et al. Separation and Departure Strategy from Uncontrolled International Space Station // Proc. of the 18th International Symposium on Space Flight Dynamics. Oct. 11–15, 2004. Munich, Germany. P. 85–90.
Bakulin V.N., Borzykh S.V., Voronin V.V. Space vehicle landing dynamics at failure of landing gear // Russian Aeronautics. 2016. V. 59. № 1. P. 23–28. https://doi.org/10.3103/S1068799816010049
Зимин В.Н., Бей Н.А. Трансформируемые антенны больших размеров для геостационарных космических аппаратов // Антенны. 2005. № 10. С. 24–27.
Юдинцев В.В. Моделирование процессов раскрытия многоэлементных конструкций космических аппаратов // Полет. 2012. № 5. С. 28–33.
Бакулин В.Н., Борзых С.В. Моделирование динамики процесса раскрытия крупногабаритных трансформируемых космических конструкций // Известия вузов. Авиационная техника. 2020. № 4. С. 50–56.
Ильясова И.Р. Динамика процесса раскрытия многозвенных солнечных батарей //Вестник Самарского государственного аэрокосмического ун-та им. С.П. Королева. 2012. Т. 35. № 4. С. 88–93.
Aslanov V., Kruglov G., Yudintsev V. Newton–Euler equations of multibody systems with changing structures for space applications // Acta Astronautica. 2011. V. 68. № 11–12. P. 2080–2087. https://doi.org/10.1016/j.actaastro
Докучаев Л.В. Нелинейная динамика летательных аппаратов с деформируемыми элементами. М.: Машиностроение, 1987. 232 с.
Бидерман В.Л. Прикладная теория механических колебаний. М.: Машиностроение, 1980. 405 с.
Ильин М.М., Колесников К.С., Саратов Ю.С. Теория колебаний. М.: МГТУ им. Н.Э. Баумана, 2003. 271 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал