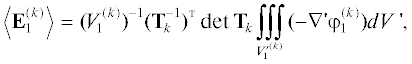Доклады Российской академии наук. Физика, технические науки, 2021, T. 498, № 1, стр. 11-16

ОБОБЩЕННОЕ ПРИБЛИЖЕНИЕ МАКСВЕЛЛА ГАРНЕТТА ДЛЯ ТЕКСТУРИРОВАННЫХ МАТРИЧНЫХ КОМПОЗИТОВ С ВКЛЮЧЕНИЯМИ В ОБОЛОЧКЕ

Академик РАН В. И. Колесников^1, *, И. В. Лавров², В. В. Бардушкин², А. П. Сычев^1, 3, **, В. Б. Яковлев^2, 4

¹ Ростовский государственный университет путей сообщения
Ростов-на-Дону, Россия

² Национальный исследовательский университет “Московский институт электронной техники”
Москва, Россия

³ Федеральный исследовательский центр Южный научный центр Российской академии наук
Ростов-на-Дону, Россия

⁴ Институт нанотехнологий микроэлектроники Российской академии наук
Москва, Россия

^* E-mail: kvi@rgups.ru
^** E-mail: alekc_sap@mail.ru

Поступила в редакцию 30.03.2021
После доработки 30.03.2021
Принята к публикации 07.04.2021

DOI: 10.31857/S268674002103010X

Полный текст (PDF)

Аннотация

Предложено обобщение приближения Максвелла Гарнетта для текстурированного матричного композита, состоящего из эллипсоидальных включений с оболочкой. С помощью указанного обобщенного приближения получено выражение для тензора эффективной диэлектрической проницаемости рассматриваемой среды. Показано, что в случае матричного композита со сферическими включениями в оболочке данное выражение совпадает с формулой, полученной в обобщенном приближении эффективного поля с выбором матрицы в качестве среды сравнения.

Ключевые слова: приближение Максвелла Гарнетта, эффективная диэлектрическая проницаемость, обобщенное приближение эффективного поля, матричный композит, включение с оболочкой

Приближение Максвелла Гарнетта (МГ) [1] широко используется для вычисления эффективных электрофизических характеристик неоднородных сред матричного типа, в том числе для прогнозирования их оптических свойств [2–4]. В [5] было установлено, что в случае, когда металлические частицы в материале изолированы друг от друга диэлектрической прослойкой (матрицей), оптические свойства пленки из такого материала качественно хорошо прогнозируются с помощью приближения МГ и его обобщений. Первоначально приближение МГ было получено Дж.К. Максвеллом Гарнеттом [1] для объяснения оптических свойств стекла с мельчайшими металлическими частицами сферической формы. В дальнейшем были получены обобщения формулы МГ для различных вариантов структуры матричных композитов с однородными включениями эллипсоидальной формы [2, 3, 6, 7]. Ключевым моментом этих обобщений являлся выбор среднего поля в матрице в качестве действующего [8]. Имеются также обобщения МГ на частные варианты сред с неоднородными включениями: со сферическими включениями с однослойной [9, 10] или многослойной [11] оболочкой, с непрерывной радиальной зависимостью диэлектрической проницаемости [11]. Тем не менее, учитывая большой практический интерес к композитам с неоднородными включениями [12, 13], имеется необходимость обобщений приближения МГ для указанных сред, позволяющих учитывать такие особенности структуры среды, как несферическая форма включений, вероятностное распределение их ориентаций и форм, а также наличие нескольких видов включений.

ПОСТАНОВКА ЗАДАЧИ И ЕЕ РЕШЕНИЕ В ОБОБЩЕННОМ ПРИБЛИЖЕНИИ МАКСВЕЛЛА ГАРНЕТТА

Рассмотрим образец объемом V статистически однородного композита, состоящего из однородной изотропной матрицы с погруженными в нее неоднородными включениями общим количеством N, каждое из которых представляет собой однородное анизотропное эллипсоидальное ядро с однородной анизотропной оболочкой, внешняя граница которой так же, как и внутренняя, является эллипсоидальной. Диэлектрические проницаемости матрицы, оболочки и ядра k-го включения обозначим ε_m, ${\mathbf{\varepsilon }}_{1}^{{(k)}}$ и ${\mathbf{\varepsilon }}_{2}^{{(k)}}$, $k = 1,2$, ..., N. Полуоси внешней $S_{1}^{{(k)}}$ и внутренней $S_{2}^{{(k)}}$ границ оболочки k-го включения обозначим $a_{{11}}^{{(k)}}$, $a_{{12}}^{{(k)}}$, $a_{{13}}^{{(k)}}$ и $a_{{21}}^{{(k)}}$, $a_{{22}}^{{(k)}}$, $a_{{23}}^{{(k)}}$ соответственно, объемную долю ядра в нем – ${{{v}}_{k}}$, объем всего k-го включения – ${{V}_{k}}$, объемную долю всех включений в образце – f. Очевидно, что

$\begin{gathered} {{{v}}_{k}} = \frac{{a_{{21}}^{{(k)}}a_{{22}}^{{(k)}}a_{{23}}^{{(k)}}}}{{a_{{11}}^{{(k)}}a_{{12}}^{{(k)}}a_{{13}}^{{(k)}}}},\quad {{V}_{k}} = \frac{{4\pi }}{3}a_{{11}}^{{(k)}}a_{{12}}^{{(k)}}a_{{13}}^{{(k)}}, \\ k = 1,2, \ldots ,N. \\ \end{gathered} $

Пусть к границе $S$ данного образца приложено постоянное электрическое поле напряженностью ${{{\mathbf{E}}}_{0}}$. Тензор ${\mathbf{\varepsilon }}{\text{*}}$ эффективных диэлектрических характеристик образца данного композита связывает средние по объему образца векторы электрической индукции и напряженности электрического поля:

$\left\langle {\mathbf{D}} \right\rangle = {\mathbf{\varepsilon }}{\text{*}}\left\langle {\mathbf{E}} \right\rangle .$

Для $\left\langle {\mathbf{E}} \right\rangle $ при отсутствии в нем двойных поляризационных слоев можно написать выражение

(1)

$\begin{gathered} \left\langle {\mathbf{E}} \right\rangle = (1 - f)\langle {{{\mathbf{E}}}^{{(m)}}}\rangle + f{{({{V}_{{inc}}})}^{{ - 1}}} \times \\ \times \;\sum\limits_{k = 1}^N {{{V}_{k}}} ((1 - {{{v}}_{k}})\langle {\mathbf{E}}_{1}^{{(k)}}\rangle + {{{v}}_{k}}\langle {\mathbf{E}}_{2}^{{(k)}}\rangle ), \\ \end{gathered} $

где $\left\langle {{{{\mathbf{E}}}^{{(m)}}}} \right\rangle $, $\left\langle {{\mathbf{E}}_{1}^{{(k)}}} \right\rangle $ и $\left\langle {{\mathbf{E}}_{2}^{{(k)}}} \right\rangle $ – средние напряженности поля в матрице, в оболочке и ядре k-го включения соответственно; ${{V}_{{inc}}} = fV$ – объем всех включений в образце. Аналогично (1), для средней поляризации образца имеем

(2)

$\begin{gathered} \left\langle {\mathbf{P}} \right\rangle = (1 - f)\left\langle {{{{\mathbf{P}}}^{{(m)}}}} \right\rangle + f{{({{V}_{{inc}}})}^{{ - 1}}} \times \\ \times \;\sum\limits_{k = 1}^N {{{V}_{k}}} ((1 - {{{v}}_{k}})\left\langle {{\mathbf{P}}_{1}^{{(k)}}} \right\rangle + {{{v}}_{k}}\left\langle {{\mathbf{P}}_{2}^{{(k)}}} \right\rangle ). \\ \end{gathered} $

Векторы поляризации и напряженности электрического поля в матрице, в оболочке и ядре k-го включения связаны материальными уравнениями

(3)

$\begin{gathered} {{{\mathbf{P}}}^{{(m)}}}({\mathbf{x}}) = {{\chi }_{m}}{{{\mathbf{E}}}^{{(m)}}}({\mathbf{x}}),\quad {\mathbf{P}}_{1}^{{(k)}}({\mathbf{x}}) = {\mathbf{\chi }}_{1}^{{(k)}}{\mathbf{E}}_{1}^{{(k)}}({\mathbf{x}}), \\ {\mathbf{P}}_{2}^{{(k)}}({\mathbf{x}}) = {\mathbf{\chi }}_{2}^{{(k)}}{\mathbf{E}}_{2}^{{(k)}}({\mathbf{x}}), \\ \end{gathered} $

где ${{\chi }_{m}} = {{(4\pi )}^{{ - 1}}}({{\varepsilon }_{m}} - 1)$, ${\mathbf{\chi }}_{1}^{{(k)}} = {{(4\pi )}^{{ - 1}}}({\mathbf{\varepsilon }}_{1}^{{(k)}} - {\mathbf{I}})$, ${\mathbf{\chi }}_{2}^{{(k)}}$ = = ${{(4\pi )}^{{ - 1}}}({\mathbf{\varepsilon }}_{2}^{{(k)}} - {\mathbf{I}})$ – восприимчивости матрицы, оболочки и ядра k-го включения соответственно. Тензор эффективной восприимчивости образца композита ${\mathbf{\chi }}{\text{*}}$, определяемый уравнением

(4)

$\left\langle {\mathbf{P}} \right\rangle = {\mathbf{\chi }}{\text{*}}\left\langle {\mathbf{E}} \right\rangle ,$

связан с ${\mathbf{\varepsilon }}{\text{*}}$ соотношением

(5)

${\mathbf{\varepsilon }}{\text{*}} = {\mathbf{I}} + 4\pi {\mathbf{\chi }}{\text{*}}.$

Подставляя (3), (4), (1) в (2) и упрощая, получим уравнение

(6)

$\begin{gathered} (1 - f)({\mathbf{\chi }}{\text{*}} - {{\chi }_{m}}{\mathbf{I}})\left\langle {{{{\mathbf{E}}}^{{(m)}}}} \right\rangle = \\ \; = \frac{f}{{{{V}_{{inc}}}}}\sum\limits_{k = 1}^N {{{V}_{k}}} \left( {(1 - {{{v}}_{k}})({\mathbf{\chi }}_{1}^{{(k)}} - {\mathbf{\chi }}{\text{*}})\left\langle {{\mathbf{E}}_{1}^{{(k)}}} \right\rangle + } \right. \\ \left. { + \;{{{v}}_{k}}({\mathbf{\chi }}_{2}^{{(k)}} - {\mathbf{\chi }}{\text{*}})\left\langle {{\mathbf{E}}_{2}^{{(k)}}} \right\rangle } \right). \\ \end{gathered} $

Следуя [8], определим обобщение приближения МГ на матричный композит с включениями в оболочке как приближение, при котором средние значения напряженности электрического поля в оболочке и ядре конкретного включения с номером k связаны со средней напряженностью поля в матрице так же, как и в таком же уединенном включении в бесконечной матрице с однородным приложенным полем, т.е.

(7)

$\left\langle {{\mathbf{E}}_{1}^{{(k)}}} \right\rangle = {\mathbf{\lambda }}_{1}^{{(k)}}\left\langle {{{{\mathbf{E}}}^{{(m)}}}} \right\rangle ,\quad \left\langle {{\mathbf{E}}_{2}^{{(k)}}} \right\rangle = {\mathbf{\lambda }}_{2}^{{(k)}}\left\langle {{{{\mathbf{E}}}^{{(m)}}}} \right\rangle ,$

где ${\mathbf{\lambda }}_{1}^{{(k)}}$ и ${\mathbf{\lambda }}_{2}^{{(k)}}$ – тензоры 2-го ранга, зависящие от геометрической формы включений и от их материальных свойств, а также от материальных свойств матрицы; их конкретный вид будет найден позже.

Подставляя (7) в (6) и выражая ${\mathbf{\chi }}{\text{*}}$ из (5) через ${\mathbf{\varepsilon }}{\text{*}}$, получим

(8)

$\begin{gathered} (1 - f)({\mathbf{\varepsilon }}{\text{*}} - {{\varepsilon }_{m}}{\mathbf{I}})\left\langle {{{{\mathbf{E}}}^{{(m)}}}} \right\rangle = \\ = \;\sum\limits_{k = 1}^N {{{w}_{k}}} ((1 - {{{v}}_{k}})({\mathbf{\varepsilon }}_{1}^{{(k)}} - {\mathbf{\varepsilon }}{\text{*}}){\mathbf{\lambda }}_{1}^{{(k)}} + \\ + \;{{{v}}_{k}}({\mathbf{\varepsilon }}_{2}^{{(k)}} - {\mathbf{\varepsilon }}{\text{*}}){\mathbf{\lambda }}_{2}^{{(k)}})\left\langle {{{{\mathbf{E}}}^{{(m)}}}} \right\rangle , \\ \end{gathered} $

где ${{w}_{k}} = {{{{V}_{k}}} \mathord{\left/ {\vphantom {{{{V}_{k}}} V}} \right. \kern-0em} V}$ – объемная доля k-го включения в образце. Уравнение (8) должно выполняться при любом значении $\left\langle {{{{\mathbf{E}}}^{{(m)}}}} \right\rangle $, зависящем непрерывно от ${{{\mathbf{E}}}_{0}}$, поэтому (8) влечет за собой тензорное равенство, выражая из которого ${\mathbf{\varepsilon }}{\text{*}}$, имеем

(9)

$\begin{gathered} {\mathbf{\varepsilon }}{\text{*}}\, = \,\left[ {(1\, - \,f){{\varepsilon }_{m}}{\mathbf{I}}\, + \,\sum\limits_{k = 1}^N {{{w}_{k}}} ((1\, - \,{{{v}}_{k}}){\mathbf{\varepsilon }}_{1}^{{(k)}}{\mathbf{\lambda }}_{1}^{{(k)}}\, + \,{{{v}}_{k}}{\mathbf{\varepsilon }}_{2}^{{(k)}}{\mathbf{\lambda }}_{2}^{{(k)}})} \right] \times \\ \times \;{{\left[ {(1 - f){\mathbf{I}} + \sum\limits_{k = 1}^N {{{w}_{k}}} ((1 - {{{v}}_{k}}){\mathbf{\lambda }}_{1}^{{(k)}} + {{{v}}_{k}}{\mathbf{\lambda }}_{2}^{{(k)}})} \right]}^{{ - 1}}}. \\ \end{gathered} $

Введем обозначения:

(10)

$\begin{gathered} {\mathbf{\lambda }}_{{}}^{{(k)}} = (1 - {{{v}}_{k}}){\mathbf{\lambda }}_{1}^{{(k)}} + {{{v}}_{k}}{\mathbf{\lambda }}_{2}^{{(k)}}, \\ \kappa _{{}}^{{(k)}} = (1 - {{{v}}_{k}}){\mathbf{\varepsilon }}_{1}^{{(k)}}{\mathbf{\lambda }}_{1}^{{(k)}} + {{{v}}_{k}}{\mathbf{\varepsilon }}_{2}^{{(k)}}{\mathbf{\lambda }}_{2}^{{(k)}}, \\ k = 1,2, \ldots ,N. \\ \end{gathered} $

Вводя средние значения тензоров ${\mathbf{\lambda }}_{{}}^{{(k)}}$ и $\kappa _{{}}^{{(k)}}$ по всем включениям

(11)

$\left\langle {\mathbf{\lambda }} \right\rangle = \frac{1}{f}\sum\limits_{k = 1}^N {{{w}_{k}}} {{{\mathbf{\lambda }}}^{{(k)}}},\quad \left\langle \kappa \right\rangle = \frac{1}{f}\sum\limits_{k = 1}^N {{{w}_{k}}} {{\kappa }^{{(k)}}},$

перепишем (9) в виде

(12)

${\mathbf{\varepsilon }}* = \left[ {(1 - f){{\varepsilon }_{m}}{\mathbf{I}} + f\left\langle \kappa \right\rangle } \right]{{\left[ {(1 - f){\mathbf{I}} + f\left\langle {\mathbf{\lambda }} \right\rangle } \right]}^{{ - 1}}},$

аналогичном соотношению для тензора эффективной диэлектрической проницаемости матричного композита с однородными анизотропными эллипсоидальными включениями, полученном в [7], только в данном случае тензоры ${\mathbf{\lambda }}$ и $\kappa $, усредняемые по всем включениям, имеют более сложный вид.

ВЫЧИСЛЕНИЕ ТЕНЗОРОВ, СВЯЗЫВАЮЩИХ СРЕДНИЕ НАПРЯЖЕННОСТИ ПОЛЯ

Пусть уединенное k-е включение погружено в бесконечную матрицу с приложенным однородным электрическим полем напряженностью ${{{\mathbf{E}}}_{0}}$. Аналогично предположениям, принятым в [14], будем считать, что внутренняя $S_{2}^{{(k)}}$ и внешняя $S_{1}^{{(k)}}$ границы оболочки становятся софокусными эллипсоидами после линейного неортогонального преобразования

(13)

${\mathbf{r}} = {{{\mathbf{T}}}_{k}}{\mathbf{r}}_{k}^{'},$

устраняющего анизотропию диэлектрических свойств оболочки k-го включения. Здесь r = = ${{({{x}^{1}}\,{{x}^{2}}\,{{x}^{3}})}^{{\text{т}}}}$, ${\mathbf{r}}_{k}^{'} = {{(x_{k}^{{1{\text{'}}}}\;x_{k}^{{2{\text{'}}}}\;x_{k}^{{3{\text{'}}}})}^{{\text{т}}}}$ – векторы-столбцы координат текущей точки в исходной системе координат ${{x}^{1}}{{x}^{2}}{{x}^{3}}$ и системе $x_{k}^{{1{\text{'}}}}x_{k}^{{2{\text{'}}}}x_{k}^{{3{\text{'}}}}$, полученной из нее преобразованием (13). Связь матрицы преобразования (13) с тензором диэлектрической проницаемости оболочки включения имеет вид [14]

(14)

${\mathbf{\varepsilon }}_{1}^{{(k)}} = {{{\mathbf{T}}}_{k}}{{\left( {{{{\mathbf{T}}}_{k}}} \right)}^{{\text{т}}}}.$

При преобразовании (13) поверхности-эллипсоиды $S_{1}^{{(k)}}$, $S_{2}^{{(k)}}$ трансформируются соответственно в софокусные поверхности-эллипсоиды $S_{1}^{{'(k)}}$, $S_{2}^{{'(k)}}$, полуоси которых обозначим как $a_{{11{\text{'}}}}^{{(k)}}$, $a_{{12{\text{'}}}}^{{(k)}}$, $a_{{13{\text{'}}}}^{{(k)}}$ и $a_{{21{\text{'}}}}^{{(k)}}$, $a_{{22{\text{'}}}}^{{(k)}}$, $a_{{23{\text{'}}}}^{{(k)}}$. Условие (14) определяет преобразование (13) с точностью до поворота, поэтому можно считать, что оси системы $x_{k}^{{1{\text{'}}}}x_{k}^{{2{\text{'}}}}x_{k}^{{3{\text{'}}}}$ направлены вдоль геометрических осей поверхностей-эллипсоидов $S_{1}^{{'(k)}}$, $S_{2}^{{'(k)}}$.

В данных условиях электрическое поле в ядре включения – однородное с напряженностью [14]

(15)

${\mathbf{E}}_{2}^{{(k)}} = {\mathbf{\lambda }}_{{20}}^{{(k)}}{{{\mathbf{E}}}_{0}},$

где

(16)

$\begin{gathered} {\mathbf{\lambda }}_{{20}}^{{(k)}} = [({\mathbf{I}} + {{({{\varepsilon }_{m}})}^{{ - 1}}}{\mathbf{L}}_{1}^{{(k)}}({\mathbf{\varepsilon }}_{1}^{{(k)}} - {{\varepsilon }_{m}}{\mathbf{I}})) \times \\ \times \;({\mathbf{I}} + ({\mathbf{L}}_{{2,0}}^{{'(k)}} - {{{v}}_{k}}{\mathbf{L}}_{{1,0}}^{{'(k)}})({\mathbf{\varepsilon }}_{2}^{{(k)}} - {\mathbf{\varepsilon }}_{1}^{{(k)}})) + \\ + \;{{{v}}_{k}}{{({{\varepsilon }_{m}})}^{{ - 1}}}{\mathbf{L}}_{1}^{{(k)}}({\mathbf{\varepsilon }}_{2}^{{(k)}} - {\mathbf{\varepsilon }}_{1}^{{(k)}}){{]}^{{ - 1}}}; \\ \end{gathered} $

${\mathbf{L}}_{1}^{{(k)}}$ – тензор геометрических факторов эллипсоида с поверхностью $S_{1}^{{(k)}}$, его главные компоненты [14]

(17)

$\begin{gathered} L_{{1i}}^{{(k)}} = \frac{{a_{{11}}^{{(k)}}a_{{12}}^{{(k)}}a_{{13}}^{{(k)}}}}{2}\int\limits_0^{ + \infty } {\frac{{du}}{{[u + {{{(a_{{1i}}^{{(k)}})}}^{2}}]R_{1}^{{(k)}}(u)}}} , \\ i = 1,2,3; \\ \end{gathered} $

$\begin{gathered} R_{1}^{{(k)}}(u) = {{[(u + {{(a_{{11}}^{{(k)}})}^{2}})(u + {{(a_{{12}}^{{(k)}})}^{2}})(u + {{(a_{{13}}^{{(k)}})}^{2}})]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\quad \\ k = 1,2, \ldots ,N; \\ \end{gathered} $

${\mathbf{L}}_{{1,0}}^{{'(k)}}$, ${\mathbf{L}}_{{2,0}}^{{'(k)}}$ – тензоры обобщенных геометрических факторов эллипсоидов с внешними границами $S_{1}^{{(k)}}$, $S_{2}^{{(k)}}$ соответственно с учетом анизотропии оболочки k-го включения в системе координат ${{x}^{1}}{{x}^{2}}{{x}^{3}}$, определяемые формулами [14]

${\mathbf{L}}_{{j,0}}^{{'(k)}} = {{({\mathbf{T}}_{k}^{{ - 1}})}^{{\text{т}}}}{\mathbf{L}}_{j}^{{'(k)}}{\mathbf{T}}_{k}^{{ - 1}},\quad j = 1,2,$

где тензоры ${\mathbf{L}}_{1}^{{'(k)}}$, ${\mathbf{L}}_{2}^{{'(k)}}$ – диагональные с главными компонентами

$\begin{gathered} L_{{ji'}}^{{'(k)}} = \frac{{a_{{j1'}}^{{(k)}}a_{{j2'}}^{{(k)}}a_{{j3'}}^{{(k)}}}}{2}\int\limits_0^{ + \infty } {\frac{{du}}{{{{{[u + (a_{{ji'}}^{{(k)}})]}}^{2}}\tilde {R}_{j}^{{(k)}}(u)}},} \\ i{\text{'}} = 1{\text{'}},\;2{\text{'}},\;3{\text{'}};\quad j = 1,\;2, \\ \end{gathered} $

$\tilde {R}_{j}^{{(k)}}(u) = {{[(u + {{(a_{{j1'}}^{{(k)}})}^{2}})(u + {{(a_{{j2'}}^{{(k)}})}^{2}})(u + {{(a_{{j3'}}^{{(k)}})}^{2}})]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$

Из (15) вытекает, что средняя по объему напряженность поля в ядре равна

(18)

$\left\langle {{\mathbf{E}}_{2}^{{(k)}}} \right\rangle = {\mathbf{\lambda }}_{{20}}^{{(k)}}{{{\mathbf{E}}}_{0}}.$

Найдем среднюю по объему напряженность электрического поля в оболочке включения. Потенциал электрического поля в оболочке имеет выражение [14]

(19)

$\begin{gathered} \varphi _{1}^{{(k)}} = (({\mathbf{\beta }}_{1}^{{(k)}} + {\mathbf{N}}_{0}^{{'(k)}}(\xi {\text{'}}){\mathbf{\alpha }}_{1}^{{(k)}}){{{\mathbf{E}}}_{0}},{\mathbf{r}}), \\ {\mathbf{r}} \in V_{1}^{{(k)}},\quad 0 \leqslant \xi {\text{'}} \leqslant t{\text{'}}, \\ \end{gathered} $

где $V_{1}^{{(k)}}$ – объем, занимаемый оболочкой k-го включения;

(20)

$\begin{gathered} {\mathbf{\alpha }}_{1}^{{(k)}} = ({\mathbf{\varepsilon }}_{2}^{{\,(k)}} - {\mathbf{\varepsilon }}_{1}^{{(k)}}){\mathbf{\lambda }}_{{20}}^{{(k)}}, \\ {\mathbf{\beta }}_{1}^{{(k)}} = - ({\mathbf{I}} + {\mathbf{L}}_{{2,0}}^{{'(k)}}({\mathbf{\varepsilon }}_{2}^{{(k)}} - {\mathbf{\varepsilon }}_{1}^{{\,(k)}})){\mathbf{\lambda }}_{{20}}^{{(k)}}, \\ \end{gathered} $

${\mathbf{N}}_{0}^{{'(k)}}(\xi {\text{'}})$ – тензорная функция, определяемая формулой

${\mathbf{N}}_{0}^{{'(k)}}(\xi {\text{'}}) = {{({\mathbf{T}}_{k}^{{ - 1}})}^{{\text{т}}}}{\mathbf{N}}_{{}}^{{'(k)}}(\xi {\text{'}}){\mathbf{T}}_{k}^{{ - 1}},$

где тензорная функция ${\mathbf{N}}_{{}}^{{'(k)}}(\xi {\text{'}})$ – диагональная с главными компонентами

$\begin{gathered} N_{{i'}}^{{'(k)}}(\xi {\text{'}}) = \frac{{a_{{21'}}^{{(k)}}a_{{22'}}^{{(k)}}a_{{23'}}^{{(k)}}}}{2}\int\limits_{\xi '}^{ + \infty } {\frac{{du}}{{[u + {{{(a_{{2i'}}^{{(k)}})}}^{2}}]\tilde {R}_{u}^{{(k)}}}}} , \\ i{\text{'}} = 1{\text{'}},\;2{\text{'}},\;3{\text{'}};\quad 0 \leqslant \xi {\text{'}} \leqslant t{\text{'}}; \\ \end{gathered} $

$\tilde {R}_{u}^{{(k)}} = {{[(u + {{(a_{{21'}}^{{(k)}})}^{2}})(u + {{(a_{{22'}}^{{(k)}})}^{2}})(u + {{(a_{{23'}}^{{(k)}})}^{2}})]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}};$

$t{\kern 1pt} '$ – “шаг софокусности” эллипсоидов $S_{1}^{{'(k)}}$, $S_{2}^{{'(k)}}$:

$t{\text{'}} = {{(a_{{1i'}}^{{(k)}})}^{2}} - {{(a_{{2i'}}^{{(k)}})}^{2}},\quad i{\text{'}} = 1{\text{'}},\;2{\text{'}},\;3{\text{'}}.$

Для средней напряженности поля в оболочке имеем

(21)

$\begin{gathered} \left\langle {{\mathbf{E}}_{1}^{{(k)}}} \right\rangle = {{(V_{1}^{{(k)}})}^{{ - 1}}}\iiint\limits_{V_{1}^{{(k)}}} {{\mathbf{E}}_{1}^{{(k)}}dV} = \\ = \;{{(V_{1}^{{(k)}})}^{{ - 1}}}\iiint\limits_{V_{1}^{{(k)}}} {( - \nabla \varphi _{1}^{{(k)}})dV}. \\ \end{gathered} $

Поскольку в системе координат ${{x}^{1}}{{x}^{2}}{{x}^{3}}$ тензоры квадратичных форм поверхностей-эллипсоидов $S_{1}^{{(k)}}$ и $S_{2}^{{(k)}}$, ограничивающих объем $V_{1}^{{(k)}}$, вообще говоря, не диагональны, целесообразно в (21) перейти в систему $x_{k}^{{1'}}x_{k}^{{2'}}x_{k}^{{3'}}$, сделав замену (13). Учтя правило преобразования градиента [14], а также то, что якобиан преобразования (13) ${\text{det}}{\mathbf{T}}_{k}^{{}}$ = = const, получим

(22)

где $\nabla {\text{'}}\varphi _{1}^{{(k)}}$ – градиент потенциала в оболочке в системе координат $x_{k}^{{1'}}x_{k}^{{2'}}x_{k}^{{3'}}$, $V_{1}^{{'(k)}}$ – образ области $V_{1}^{{(k)}}$ при преобразовании (13). Переходя в (22) от объемного интеграла к поверхностным, получим

(23)

$\begin{gathered} \left\langle {{\mathbf{E}}_{1}^{{(k)}}} \right\rangle = {{(V_{1}^{{(k)}})}^{{ - 1}}}{{({\mathbf{T}}_{k}^{{ - 1}})}^{{\text{т}}}}\det {\mathbf{T}}_{k}^{{}} \times \\ \times \;\left[ { - \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{S_{1}^{{'(k)}}} {\varphi _{1}^{{(k)}}{\mathbf{n}}_{1}^{'}} dS\,{\text{'}} + \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{S_{2}^{{'(k)}}} {\varphi _{1}^{{(k)}}{\mathbf{n}}_{2}^{'}} dS\,{\text{'}}} \right], \\ \end{gathered} $

где ${\mathbf{n}}_{1}^{'}$, ${\mathbf{n}}_{2}^{'}$ – внешние единичные нормали к поверхностям $S_{1}^{{'(k)}}$, $S_{2}^{{'(k)}}$. С учетом (13) перепишем (19) в виде

$\begin{gathered} \varphi _{1}^{{(k)}} = ({{({\mathbf{T}}_{k}^{{}})}^{{\text{т}}}}({\mathbf{\beta }}_{1}^{{(k)}} + {\mathbf{N}}_{0}^{{'(k)}}(\xi {\text{'}}){\mathbf{\alpha }}_{1}^{{(k)}}){{{\mathbf{E}}}_{0}},{\mathbf{r}}{\text{'}}), \\ {\mathbf{r}}{\text{'}} \in V_{1}^{{'(k)}};\quad 0 \leqslant \xi {\text{'}} \leqslant t{\text{'}}. \\ \end{gathered} $

На поверхности $S_{2}^{{'(k)}}$ имеем $\xi {\text{'}} = 0$, ${\mathbf{N}}_{0}^{{'(k)}}(0)$ = ${\mathbf{L}}_{{2,0}}^{{'(k)}}$ [14], поэтому $\varphi _{1}^{{(k)}}$ на $S_{2}^{{'(k)}}$ имеет вид

(24)

${{\left. {\varphi _{1}^{{(k)}}} \right|}_{{S_{2}^{{'(k)}}}}} = ({{({\mathbf{T}}_{k}^{{}})}^{{\text{т}}}}({\mathbf{\beta }}_{1}^{{(k)}} + {\mathbf{L}}_{{2,0}}^{{'(k)}}{\mathbf{\alpha }}_{1}^{{(k)}}){{{\mathbf{E}}}_{0}},{{\left. {{\mathbf{r}}{\text{'}}} \right|}_{{S_{2}^{{'(k)}}}}}).$

Аналогично на поверхности $S_{1}^{{'(k)}}$ имеем $\xi {\text{'}} = t{\text{'}}$, ${\mathbf{N}}_{0}^{{'(k)}}(t{\text{'}}) = {{{v}}_{k}}{\mathbf{L}}_{{1,0}}^{{'(k)}}$, поэтому

(25)

${{\left. {\varphi _{1}^{{(k)}}} \right|}_{{S_{1}^{{'(k)}}}}} = ({{({\mathbf{T}}_{k}^{{}})}^{{\text{т}}}}({\mathbf{\beta }}_{1}^{{(k)}} + {{{v}}_{k}}{\mathbf{L}}_{{1,0}}^{{'(k)}}{\mathbf{\alpha }}_{1}^{{(k)}}){{{\mathbf{E}}}_{0}},{{\left. {{\mathbf{r}}{\text{'}}} \right|}_{{S_{1}^{{'(k)}}}}}).$

Подставим (25) в интеграл по поверхности $S_{1}^{{'(k)}}$ в (23):

$\begin{gathered} \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{S_{1}^{{'(k)}}} {\varphi _{1}^{{(k)}}{\mathbf{n}}_{1}^{'}} dS\,{\text{'}} = \\ = \;\left( {{{{({\mathbf{T}}_{k}^{{}})}}^{{\text{т}}}}({\mathbf{\beta }}_{1}^{{(k)}} + {{{v}}_{k}}{\mathbf{L}}_{{1,0}}^{{'(k)}}{\mathbf{\alpha }}_{1}^{{(k)}}){{{\mathbf{E}}}_{0}},\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{S_{1}^{{'(k)}}} {{\mathbf{r}}{\text{'}} \otimes {\mathbf{n}}_{1}^{'}} dS\,{\text{'}}} \right). \\ \end{gathered} $

Вычисляя поверхностный интеграл, получим

$\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{S_{1}^{{'(k)}}} {{\mathbf{r}}{\text{'}} \otimes {\mathbf{n}}_{1}^{'}} dS\,{\text{'}} = \frac{{4\pi }}{3}a_{{11'}}^{{(k)}}a_{{12'}}^{{(k)}}a_{{13'}}^{{(k)}}{\mathbf{I}}.$

Таким образом,

(26)

$\begin{gathered} \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{S_{1}^{{'(k)}}} {\varphi _{1}^{{(k)}}{\mathbf{n}}_{1}^{'}} dS\,{\text{'}} = \frac{{4\pi }}{3}a_{{11'}}^{{(k)}}a_{{12'}}^{{(k)}}a_{{13'}}^{{(k)}} \times \\ \times \;{{({\mathbf{T}}_{k}^{{}})}^{{\text{т}}}}({\mathbf{\beta }}_{1}^{{(k)}} + {{{v}}_{k}}{\mathbf{L}}_{{1,0}}^{{'(k)}}{\mathbf{\alpha }}_{1}^{{(k)}}){{{\mathbf{E}}}_{0}}. \\ \end{gathered} $

Аналогично с учетом (24) для интеграла по поверхности $S_{2}^{{'(k)}}$ имеем

(27)

$\begin{gathered} \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{S_{2}^{{'(k)}}} {\varphi _{1}^{{(k)}}{\mathbf{n}}_{2}^{'}} dS\,{\text{'}} = \\ = \;\frac{{4\pi }}{3}a_{{21'}}^{{(k)}}a_{{22'}}^{{(k)}}a_{{23'}}^{{(k)}}{{({\mathbf{T}}_{k}^{{}})}^{{\text{т}}}}({\mathbf{\beta }}_{1}^{{(k)}} + {\mathbf{L}}_{{2,0}}^{{'(k)}}{\mathbf{\alpha }}_{1}^{{(k)}}){{{\mathbf{E}}}_{0}}. \\ \end{gathered} $

Подставляя (26), (27) в (23), получим

(28)

$\langle {\mathbf{E}}_{1}^{{(k)}}\rangle \, = \,{{(V_{1}^{{(k)}})}^{{ - 1}}}[ - V_{1}^{{(k)}}{\mathbf{\beta }}_{1}^{{(k)}}\, + \,V_{2}^{{(k)}}({\mathbf{L}}_{{2,0}}^{{'(k)}}\, - \,{\mathbf{L}}_{{1,0}}^{{'(k)}}){\mathbf{\alpha }}_{1}^{{(k)}}]{{{\mathbf{E}}}_{0}},$

где $V_{2}^{{(k)}} = \frac{{4\pi }}{3}a_{{21}}^{{(k)}}a_{{22}}^{{(k)}}a_{{23}}^{{(k)}}$ – объем ядра k-го включения.

С учетом (20) перепишем (28) в виде

(29)

$\begin{gathered} \left\langle {{\mathbf{E}}_{1}^{{(k)}}} \right\rangle = \frac{1}{{1 - {{{v}}_{k}}}}((1 - {{{v}}_{k}}){\mathbf{I}} + \\ + \,({\mathbf{L}}_{{2,0}}^{{'(k)}} - {{{v}}_{k}}{\mathbf{L}}_{{1,0}}^{{'(k)}})({\mathbf{\varepsilon }}_{2}^{{(k)}} - {\mathbf{\varepsilon }}_{1}^{{(k)}})){\mathbf{\lambda }}_{{20}}^{{(k)}}{{{\mathbf{E}}}_{0}}. \\ \end{gathered} $

Поскольку средняя напряженность поля в матрице при наличии в ней единственного включения равна ${{{\mathbf{E}}}_{0}}$, из (29) следует вид тензора ${\mathbf{\lambda }}_{1}^{{(k)}}$:

(30)

$\begin{gathered} {\mathbf{\lambda }}_{1}^{{(k)}} = \frac{1}{{1 - {{{v}}_{k}}}}((1 - {{{v}}_{k}}){\mathbf{I}} + \\ + \,({\mathbf{L}}_{{2,0}}^{{'(k)}} - {{{v}}_{k}}{\mathbf{L}}_{{1,0}}^{{'(k)}})({\mathbf{\varepsilon }}_{2}^{{(k)}} - {\mathbf{\varepsilon }}_{1}^{{(k)}})){\mathbf{\lambda }}_{{20}}^{{(k)}}, \\ \end{gathered} $

где ${\mathbf{\lambda }}_{{20}}^{{(k)}}$ определяется из (16). Аналогично из (18) следует вид тензора ${\mathbf{\lambda }}_{2}^{{(k)}}$:

(31)

${\mathbf{\lambda }}_{2}^{{(k)}} = {\mathbf{\lambda }}_{{20}}^{{(k)}}.$

Таким образом, обобщенным приближением МГ для матричного композита с эллипсоидальными включениями с эллипсоидальной оболочкой можно считать формулу (12), где используемые в нем тензорные величины определяются выражениями (10), (11), (30), (31).

ПРИМЕРЫ ПРИМЕНЕНИЯ ОБОБЩЕННОГО ПРИБЛИЖЕНИЯ МАКСВЕЛЛА ГАРНЕТТА

1. Непосредственно проверяется, что в предельных случаях композита с однородными включениями, т.е. при отсутствии ядра либо оболочки у всех включений, либо при совпадающих материальных характеристиках ядер и оболочек, результат по формулам (12), (10), (11), (30), (31) совпадает с результатом, полученным в [7] для композита с однородными эллипсоидальными включениями.

2. Рассмотрим случай, когда оболочки всех включений изотропные, т.е. ${\mathbf{\varepsilon }}_{1}^{{(k)}} = \varepsilon _{1}^{{(k)}}{\mathbf{I}}$, и главные оси тензоров ${\mathbf{\varepsilon }}_{2}^{{(k)}}$ всех включений совпадают с осями их ядер. Тогда $S_{2}^{{(k)}}$ и $S_{1}^{{(k)}}$ – софокусные эллипсоиды, их оси совпадают с главными осями тензора ${\mathbf{\varepsilon }}_{2}^{{(k)}}$. В этом случае [14]

$\begin{gathered} {\mathbf{L}}_{{1,0}}^{{'(k)}} = {{(\varepsilon _{1}^{{(k)}})}^{{ - 1}}}{\mathbf{L}}_{1}^{{(k)}}, \\ {\mathbf{L}}_{{2,0}}^{{'(k)}} = {{(\varepsilon _{1}^{{(k)}})}^{{ - 1}}}{\mathbf{L}}_{2}^{{(k)}},\quad k = 1,\;2,\; \ldots ,\;N, \\ \end{gathered} $

где главные значения тензора ${\mathbf{L}}_{2}^{{(k)}}$ имеют выражения, аналогичные (17), с заменой полуосей $S_{1}^{{(k)}}$ на полуоси $S_{2}^{{(k)}}$. Для тензоров ${\mathbf{\lambda }}_{{20}}^{{(k)}}$, ${\mathbf{\lambda }}_{1}^{{(k)}}$, ${\mathbf{\lambda }}_{{}}^{{(k)}}$, $\kappa _{{}}^{{(k)}}$ имеем

$\begin{gathered} {\mathbf{\lambda }}_{{20}}^{{(k)}} = [({\mathbf{I}} + {{({{\varepsilon }_{m}})}^{{ - 1}}}{\mathbf{L}}_{1}^{{(k)}}(\varepsilon _{1}^{{(k)}} - {{\varepsilon }_{m}})) \times \\ \times \;({\mathbf{I}} + {{(\varepsilon _{1}^{{(k)}})}^{{ - 1}}}({\mathbf{L}}_{2}^{{(k)}} - {{{v}}_{k}}{\mathbf{L}}_{1}^{{(k)}})({\mathbf{\varepsilon }}_{2}^{{(k)}} - \varepsilon _{1}^{{(k)}}{\mathbf{I}})) + \\ + \;{{{v}}_{k}}{{({{\varepsilon }_{m}})}^{{ - 1}}}{\mathbf{L}}_{1}^{{(k)}}({\mathbf{\varepsilon }}_{2}^{{(k)}} - \varepsilon _{1}^{{(k)}}{\mathbf{I}}){{]}^{{ - 1}}}, \\ \end{gathered} $

(32)

$\begin{gathered} {\mathbf{\lambda }}_{1}^{{(k)}} = \frac{1}{{1 - {{{v}}_{k}}}}((1 - {{{v}}_{k}}){\mathbf{I}} + {{(\varepsilon _{1}^{{(k)}})}^{{ - 1}}}) \times \\ \times \;({\mathbf{L}}_{2}^{{(k)}} - {{{v}}_{k}}{\mathbf{L}}_{1}^{{(k)}})({\mathbf{\varepsilon }}_{2}^{{(k)}} - \varepsilon _{1}^{{(k)}}{\mathbf{I}})){\mathbf{\lambda }}_{{20}}^{{(k)}}, \\ \end{gathered} $

${\mathbf{\lambda }}_{{}}^{{(k)}} = ({\mathbf{I}} + {{(\varepsilon _{1}^{{(k)}})}^{{ - 1}}}({\mathbf{L}}_{2}^{{(k)}} - {{{v}}_{k}}{\mathbf{L}}_{1}^{{(k)}})({\mathbf{\varepsilon }}_{2}^{{(k)}} - \varepsilon _{1}^{{(k)}}{\mathbf{I}})){\mathbf{\lambda }}_{{20}}^{{(k)}},$

$\begin{gathered} \kappa _{{}}^{{(k)}} = [\varepsilon _{1}^{{(k)}}{\mathbf{I}} + ({{{v}}_{k}}{\mathbf{I}} + ({\mathbf{L}}_{2}^{{(k)}} - {{{v}}_{k}}{\mathbf{L}}_{1}^{{(k)}})) \times \\ \times \;({\mathbf{\varepsilon }}_{2}^{{(k)}} - \varepsilon _{1}^{{(k)}}{\mathbf{I}})]{\mathbf{\lambda }}_{{20}}^{{(k)}},\quad k = 1,\;2,\; \ldots ,\;N. \\ \end{gathered} $

Если все включения имеют одинаковую форму, материальные свойства и ориентацию, то номер включения в (32) можно опустить, а операцию усреднения в (12) снять. Тогда

${\mathbf{\varepsilon }}* = \left[ {(1 - f){{\varepsilon }_{m}}{\mathbf{I}} + f\kappa } \right]{{\left[ {(1 - f){\mathbf{I}} + f{\mathbf{\lambda }}} \right]}^{{ - 1}}},$

где ${\mathbf{\lambda }}_{{20}}^{{}}$, ${\mathbf{\lambda }}$ и $\kappa $ определяются формулами, аналогичными (32).

3. Рассмотрим композит с одинаковыми включениями с шарообразным анизотропным ядром в сферической изотропной оболочке. В этом случае

${{{v}}_{k}} = {v},\quad \varepsilon _{1}^{{(k)}} = {{\varepsilon }_{1}},\quad {\mathbf{\varepsilon }}_{2}^{{(k)}} = {{{\mathbf{\varepsilon }}}_{2}},$

${\mathbf{L}}_{1}^{{(k)}} = {\mathbf{L}}_{2}^{{(k)}} = \frac{1}{3}{\mathbf{I}},\quad k = 1,\;2,\; \ldots ,\;N,$

и для ε* в итоге по формулам (32), (12) получим

(33)

$\begin{gathered} {\mathbf{\varepsilon }}* = {{\varepsilon }_{m}}\left[ {(1 - f){\mathbf{I}}\, + \,3f{{\varepsilon }_{1}}\left\langle {\left[ {(2{{\varepsilon }_{1}}{\mathbf{I}} + {{{\mathbf{\varepsilon }}}_{2}}) + 2{v}({{{\mathbf{\varepsilon }}}_{2}} - {{\varepsilon }_{1}}{\mathbf{I}})} \right]} \right.} \right. \times \\ \times \;{{\left[ {(2{{\varepsilon }_{m}}\, + \,{{\varepsilon }_{1}})(2{{\varepsilon }_{1}}{\mathbf{I}} + {{{\mathbf{\varepsilon }}}_{2}}) + 2{v}({{\varepsilon }_{1}} - {{\varepsilon }_{m}})({{{\mathbf{\varepsilon }}}_{2}} - {{\varepsilon }_{1}}{\mathbf{I}})} \right]}^{{ - 1}}}\rangle ] \times \\ \times \;[(1 - f){\mathbf{I}} + 3{{\varepsilon }_{m}}f\langle ((2{{\varepsilon }_{1}}{\mathbf{I}} + {{{\mathbf{\varepsilon }}}_{2}}) - {v}({{{\mathbf{\varepsilon }}}_{2}} - {{\varepsilon }_{1}}{\mathbf{I}}))_{{}}^{{}} \times \\ \times \;{{\left[ {(2{{\varepsilon }_{m}}\, + \,{{\varepsilon }_{1}})(2{{\varepsilon }_{1}}{\mathbf{I}} + {{{\mathbf{\varepsilon }}}_{2}})\, + \,2{v}({{\varepsilon }_{1}} - {{\varepsilon }_{m}})({{{\mathbf{\varepsilon }}}_{2}} - {{\varepsilon }_{1}}{\mathbf{I}})} \right]}^{{ - 1}}}\rangle {{]}^{{ - 1}}}. \\ \end{gathered} $

Усреднение в (33) производится по всем ориентациям кристаллографических осей ядер включений, которое может быть проведено, как в [7], с использованием теории представлений группы вращений. Заметим, что (33) формально может быть получена как частный случай обобщенного приближения эффективного поля для данного композита, если в качестве среды сравнения взять матрицу ([15, формула (33)]).

ЗАКЛЮЧЕНИЕ

Основным результатом настоящей работы являются формулы (12), (10), (11), (30), (31), в совокупности представляющие обобщенное приближение Максвелла Гарнетта для вычисления эффективных диэлектрических характеристик матричного композита с эллипсоидальными включениями с оболочкой. Данное приближение позволяет естественным образом учитывать такие структурные особенности композита, как наличие нескольких видов включений, а также вероятностные распределения их форм и ориентаций.

Список литературы

Maxwell Garnett J.C. // Phil. Trans. R. Soc. London. 1904. V. 203. P. 385–420.
Bragg W.L., Pippard A.B. // Acta Cryst. 1953. V. 6. № 11–12. P. 865–867.
Levy O., Stroud D. // Phys. Rev. B. 1997. V. 56. № 13. P. 8035–8046.
Ораевский А.Н., Проценко И.Е. // Квантовая электроника. 2001. Т. 31. № 3. С. 252–256.
Gittleman J.I., Abeles B. // Phys. Rev. B. 1977. V. 15. № 6. P. 3273–3275.
Fricke H. // Phys. Rev. 1924. V. 24. P. 575–587.
Лавров И.В. // Экологический вестник научных центров Черноморского экономического сотрудничества. 2009. № 1. С. 52–58.
Борен К., Хафмен Д. Поглощение и рассеяние света малыми частицами. М.: Мир, 1986. 660 с.
Kerner E.H. // Proc. Phys. Soc. B. 1956. V. 69. P. 802–807.
Апресян Л.А., Власов Д.В., Задорин Д.А., Красовский В.И. // ЖТФ. 2017. Т. 87. Вып. 1. С. 10–17. https://doi.org/10.21883/JTF.2017.01.44011.1841
Sihvola A. Electromagnetic Mixing Formulas and Applications. London: The Institution of Electrical Engineers, 1999. 296 p.
Зарубин В.С., Кувыркин Г.Н., Савельева И.Ю. // Радиооптика. МГТУ им. Н.Э. Баумана. Электрон. журн. 2016. № 3. С. 29–46. https://doi.org/10.7463/rdopt.0316.0846170
Bowler N. // IEEE Trans. Dielectr. Electr. Insul. 2006. V. 13. № 4. P. 703–711.
Лавров И.В., Яковлев В.Б. // ЖТФ. 2017. Т. 87. Вып. 7. С. 963–972. https://doi.org/10.21883/JTF.2017.07.44663.1964
Колесников В.И., Бардушкин В.В., Лавров И.В., Сычев А.П., Яковлев В.Б. // ДАН. 2017. Т. 476. № 3. С. 280–284. https://doi.org/10.7868/S0869565217270081

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал