Доклады Российской академии наук. Физика, технические науки, 2021, T. 498, № 1, стр. 62-66

В регулярных волноводах любой физической природы наблюдается интерференция сигналов, пришедших по разным лучам или модам. Конструктивная интерференционная структура формируется при движении источника или приемника и когерентном суммировании сигналов, распространяющихся в воздушных или водных волноводах. Наиболее рельефно проявляется интерференция при распространении в волноводах широкополосных сигналов – в этом случае в частотно-пространственной области образуются “гребни”, представляющие собой зоны интерференционных максимумов, расположенные на поле интенсивности в виде веерных структур (рис. 1 а) [1, 2]. Характерной особенностью этих структур является их предсказуемость (описание с использованием инвариантов) и робастность (устойчивость к вариации условий распространения и координат) [1, 2].

К настоящему времени сформировался большой класс практически важных задач, которые решаются с опорой на экспериментально и теоретически обоснованную устойчивость пространственно-частотной интерференционной структуры акустических полей в широкой полосе частот и расстояний. Теоретически и экспериментально показано, что накопление мощности сигнала вдоль линий гребней интерференционной структуры может быть использовано для повышения эффективности обнаружения слабых сигналов, оценки расстояния и радиальной компоненты скорости движения [3, 4]. Отметим, что теоретические построения, описывающие свойства обсуждаемой интерференционной структуры, основаны на анализе поля интенсивности широкополосных или тональных сигналов, в которых, как известно, фазовая информация отсутствует. Вместе с тем естественно предположить, что эффективное накопление мощности сигнала в процессе его обработки можно было бы осуществить, используя для этого линии равных фаз поля звукового давления, вычисленные на фазовой плоскости. В случае существования таких “особых линий” окажется возможным дополнительное и эффективное накопление мощности слабых сигналов совместно с алгоритмами, предложенными и исследованными в [3, 4]. Такая обработка может способствовать повышению помехоустойчивости обнаружения и оценки параметров слабых сигналов, поскольку в поле гидроакустических помех такие закономерности отсутствуют.

Рассмотрим в общем виде эту задачу в трехмерном пространстве (ω, r, φ), где ω – частота источника, r – расстояние до источника, φ – интегральная фаза давления. На линиях равных фаз φ(ω, r) = const, выбранных на этой поверхности, полный дифференциал должен быть равен нулю, откуда может быть получено обыкновенное дифференциальное уравнение первого порядка, решением которого являются функции φ(ω, r). Задавая некоторое начальное условие для t₀, в любом волноводе в водной или воздушной среде можно поставить задачу Коши для выделения конкретных линий, на которых фазы постоянные, например, кратны π: ${{\varphi }_{1}}({{r}_{1}},{{\omega }_{1}}) = n\pi $. Решим этим путем задачу применительно к волноводу Пекериса, в котором на достаточно больших расстояниях поле звукового давления P может быть описано известным выражением [2]:

где z₀ и z – глубины источника и приемника соответственно, ρ₀ – плотность воды, h – толщина волновода, N – количество нормальных волн, ${{p}_{l}} = \sin \left( {\frac{{l\pi {{z}_{0}}}}{H}} \right)\sin \left( {\frac{{l\pi z}}{H}} \right)$, $l = 1,\;2,\; \ldots ,\;N$ – коэффициенты их возбуждения, $H = h + \frac{m}{{k{{\nu }_{0}}}}$ – эффективная толщина волновода, $m = \frac{{{{\rho }_{1}}}}{{{{\rho }_{0}}}}$, ρ₁ – плотность среды, $\nu _{0}^{2} = 1 - n_{0}^{2}$, ${{n}_{0}} = \frac{{{{c}_{0}}}}{{{{c}_{1}}}} < 1$, ${{c}_{1}}$ – скорость звука в подстилающем полупространстве, φ_l(ω, r) = = ${{k}_{l}}r - \omega t - \frac{\pi }{4}$ – фаза и ${{k}_{l}} = k\cos \left( {\frac{{\pi l}}{{kH}}} \right)$ – волновое число l-й нормальной волны. В этих соотношениях частоту $\omega $ и расстояние r будем считать аргументами, а время t – параметром. Выделим в выражении для давления

P(ω, r) = |P(ω, r)|${\text{exp}}[i\varphi (\omega ,r)]$

вещественную и мнимую части:

(здесь и далее глубины z₀, z и время t в обозначениях функций для краткости опускаются). Отсюда находим фазу звукового давления: где

$A(\omega ,r)\, = \,\sum\limits_{l = 1}^N {{{p}_{l}}{\text{sin}}[{{\varphi }_{l}}(\omega ,r)]} $, B(ω, r) = $\sum\limits_{l = 1}^N {{{p}_{l}}{\text{cos}}[{{\varphi }_{l}}(\omega } $, r)].

Выпишем полный дифференциал функции φ(ω, r) и, приравняв его к нулю, получим уравнение для описания линии равных фаз в рассматриваемом волноводе:

где ${{A}_{\omega }}(\omega ,r)$, ${{A}_{r}}(\omega ,r)$, ${{B}_{\omega }}(\omega ,r)$ и ${{B}_{r}}(\omega ,r)$ – частные производные по соответствующим аргументам ω и r. Вычисляя все эти производные, будем считать, что рассматривается частотная область, в пределах которой изменение количества нормальных волн N невелико и вкладом от такого изменения можно пренебречь. Подставляя их в (3), получим окончательный вид дифференциального уравнения, описывающего линии равных фаз давления в рассматриваемом волноводе: где $C = \frac{{{{S}_{1}}}}{S}$, $D = \frac{{{{S}_{2}}}}{S}$,

S = $\sum\limits_{l = 1}^N {\sum\limits_{m = 1}^N {{{p}_{l}}{{p}_{m}}{\text{cos}}\frac{{m\pi }}{{kH}}} } $cos(φ_l – φ_m),

S₂ = $\sum\limits_{l = 1}^N {\sum\limits_{m = 1}^N {{{p}_{l}}{{p}_{m}}} } $cos(φ_l – φ_m),

S₁ =  $\sum\limits_{l = 1}^N {\sum\limits_{m = 1}^N {m{{p}_{l}}{{p}_{m}}{\text{sin}}\frac{{m\pi }}{{kH}}} } $cos(φ_l – φ_m).

Дополнительный анализ и вычислительные эксперименты показывают, что параметр ${{\beta }_{\varphi }}$ из уравнения (4) в достаточно широких пределах не зависит от расстояния r и частоты ω. Аналогичным свойством обладает и параметр $D$ этого же уравнения, что дает возможность преобразовать (4):

где $A = \frac{{Dc}}{{{{\beta }_{\varphi }}}}$ – практически не зависящий от частоты и расстояния параметр. Следовательно, после замены переменной $r{\text{'}} = r - At$ уравнение (4) принимает вид $\frac{{dr{\text{'}}}}{{d\omega }} = \frac{{{{\beta }_{\varphi }}r{\text{'}}}}{\omega }$. Выполненная замена переменной фактически представляет собой происходящий во времени параллельный перенос вдоль оси расстояний всей совокупности линий равных фаз и, следовательно, всей структуры фазового поля в целом. Очевидно, что такой перенос эквивалентен движению в указанном направлении источника или приемника со скоростью, определяемой параметром А.

Заметим, что в [1–4] используется полностью аналогичное дифференциальное уравнение вида $\frac{{dr}}{{d\omega }} = \frac{{\beta r}}{\omega }$, которым в пространственно-частотной области поля интенсивности описываются линии “гребней”. При этом во многих практически важных случаях коэффициент β оказывается близок к “+1”, в связи с чем его принято называть интерференционным инвариантом [1–4]. Вид решений уравнения (4) существенно зависит от знака параметра β_φ, который подобен инварианту β, но отличается количественно и по физическому смыслу: ${{\beta }_{\varphi }} = - \left[ {1 + \frac{{\pi hC}}{{k{{H}^{2}}}}} \right]$. Если рассматривать волновод, частоты и расстояния, при которых $1 + \frac{{\pi hC}}{{k{{H}^{2}}}}$ > 0, то решениями уравнения (4) являются функции вида $r(\omega ) = \frac{a}{{{{\omega }^{{|{{\beta }_{\varphi }}|}}}}}$, и линии равных фаз оказываются подобны гиперболам. С физической точки зрения гиперболическая зависимость расстояния r от частоты ω на линиях равных фаз в волноводе Пекериса и в других реальных звуковых волноводах, как и в неограниченном пространстве, обосновывается тем, что в общем случае для достижения заданного значения интегральной фазы на бóльшей частоте колебанию требуется меньшее расстояние, а для меньшей частоты – бóльшее расстояние. Можно предположить, что такие зависимости будут обнаружены и в электромагнитных волноводах.

На рис. 1 приведены контурные графики, отображающие существенное отличие веерной структуры поля интенсивности (а) от структуры поля фазы (б) звукового давления в частотно-пространственной области. Расчеты выполнены в волноводе глубиной 200 м с параметрами дна m = 2.7 и n₀ = 0.83, скорости звука в воде 1500 м/с. Источник находится на глубине 20 м, прием осуществляется на глубине 100 м. Расчеты выполнены для диапазона частот 5–40 Гц и расстояний от 100–40 000 м. Видно, что линии равных фаз близки к гиперболам (рис. 1 б), но на этих линиях присутствуют резкие скачки фазы, обусловленные наличием в волноводе полюсов – зон дислокации фаз, которые формируются в зонах интерференционных минимумов амплитуды давления. В этих зонах резко уменьшается отношение сигнал/помеха и, как показывают расчеты и эксперименты, формируются скачки фаз в вертикальной и горизонтальной плоскости [5]. Возникают разрывы монотонной зависимости φ(ω, r). В качестве примера, более подробно иллюстрирующего выполненный анализ в описанном выше волноводе Пекериса, в диапазоне частот 100–120 Гц и на расстояниях 1000–2000 м выполнены расчеты фактической (численной) линий гребня и равных фаз, а также рассчитанной по уравнению (4) теоретической линии равных фаз. На рис. 2а представлены: выходящие из одной из точек локального максимума на частоте 100 Гц фактическая линия гребня (1), а также привязанные к этой точке начальным условием фактическая (2) и теоретическая (3) линии равных фаз.

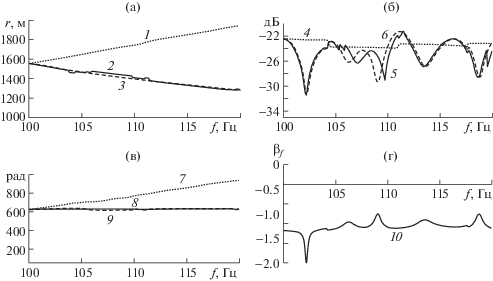
Из совпадения кривых 2 и 3 следует, что уравнение (4) достаточно точно описывает линии равных фаз, поэтому это уравнение может быть использовано для прогноза таких линий в реальных ситуациях, в том числе, при анализе экспериментальных результатов.

Далее на обсуждаемых линиях для тех же частот были рассчитаны амплитуды (рис. 2б) и фазы (рис. 2в) звукового давления. На рис. 2б видно, что линия равных фаз может пересекать несколько соседних гребней и амплитуда давления на ней может быть близкой, меньше, а на отдельных участках даже больше (кривые 5, 6), чем амплитуда на линии гребня (кривая 4). Фаза давления на линии гребня (кривая 7) в соответствии с теоретическими представлениями не постоянная, а растет с некоторым градиентом. Фазы на линии равных фаз (кривые 8, 9) постоянные – они параллельны оси абсцисс. Зависимость фазового инварианта β_φ от частоты (кривая 10) в среднем близка к “–1” и достаточно резко изменяется в зонах дислокаций – зонах с большими градиентами фазы. Расчеты, выполненные при различных условиях, показали стабильность инварианта β_φ. Таким образом, впервые установлено существование линий равных фаз и инварианта на фазовой плоскости, подобного интерференционному инварианту Чупрова, ранее полученному для описания полей интенсивности. Расчеты, выполненные для волноводов с различными параметрами, на различных частотах и расстояниях показали, что параметр β_φ из уравнения (4), так же как и параметр β, достаточно устойчив к вариации свойств среды и глубинам z и z₀. Это позволяет по аналогии с интерференционным инвариантом рассматривать β_φ как своеобразный фазовый инвариант. Вместе с тем инвариант Чупрова для поля интенсивности (будем его называть “энергетический инвариант”) для волновода Пекериса близок к “+1”, в то время как фазовый инвариант, построенный на фазовой плоскости, близок к “–1”.

Существование устойчивого фазового инварианта позволяет прогнозировать направления, по которым на фазовой плоскости возможны формирование линий постоянных фаз и сканирование с целью когерентного суммирования комплексных фурье-компонент. Как следствие, должно происходить увеличение отношения сигнал/помеха. Следует отметить, что в отличие от свободного пространства, где сканирование и накопление мощности возможны без ограничений – во всей рабочей полосе и во всем выбранном интервале расстояний – для волновода Пекериса зоны накопления мощности ограничены интервалами Δφ(ω, r) между двумя соседними дислокациями, так как в этих зонах монотонная зависимость φ(ω, r) = const прерывается, а фаза теряется.