Доклады Российской академии наук. Физика, технические науки, 2021, T. 500, № 1, стр. 21-25

Тонкие полупроводниковые квантовые кольца (закольцованные квантовые нити толщиной в несколько нанометров и диаметром до нескольких десятков нанометров) в последнее время исследуются очень активно [1–6]. Незатухающий квантовый ток (persisten–currents), управляемый эффект Ааронова–Бома, дробное квантование магнитного потока и т.д. – все эти явления чрезвычайно перспективны для квантовой электроники. В частности, в нашей недавней работе [7] показано, что тонкие квантовые кольца из-за наличия двух неэквивалентных гетерограниц обладают уникальными селекционными свойствами. Спектр электронных состояний, локализованных на кольце с фиксированными геометрическими параметрами, либо вообще пуст, либо сводится к единственному уровню, все квантовые числа которого определяются значением внешнего магнитного поля. До последнего времени это свойство колец оставалось скрытым, ибо для радиального удерживающего потенциала кольца использовались неадекватные модели. Если же использовать потенциал конечной глубины вида

где ΔE_c – скачок дна зоны проводимости на гетерогранице, r – радиальная координата, ${{R}_{{in}}}$ и ${{R}_{{ex}}}$ – соответственно внутренний и внешний радиусы кольца, то уникальность правил отбора в квантовом кольце становится очевидной. Обычно спектр полупроводниковой гетероструктуры формирует условие непрерывности логарифмической производной волновой функции на гетерогранице. В квантовых ямах, нитях и точках таких границ либо одна, либо две, но эквивалентных. И только в квантовых кольцах (хоть и тонких, но конечной толщины, что критически важно) условия сшивки на внешней и внутренней границах неэквивалентны, что и обусловливает их особые селекционные свойства. Фактически такие кольца аналогичны “плоским боровским атомам” с целочисленным орбитальным моментом, но равновесие в таком “атоме” поддерживает магнитное поле вместо ядра.

Везде в дальнейшем используются естественные единицы длины ${{r}_{0}} \equiv \hbar {\text{/}}\sqrt {2m{\text{*}}\Delta {{E}_{c}}} $ (m* – эффективная масса матричного электрона) и энергии $\varepsilon = E{\text{/}}\left| {\Delta {{E}_{c}}} \right|$. “Единица длины” r₀ – дебройлевская длина электрона на дне зоны проводимости матрицы с энергией, равной глубине потенциальной ямы кольца, ε – энергия связи электрона в кольце в “долях” от глубины ямы. Электрон, даже локализованный на кольце, большую часть времени проводит в матрице, так что изменением его эффективных свойств (массы и g-фактора) можно пренебречь. Отметим, что этот фактор играет существенную роль для восстановления энергии электрона при выключении магнитного поля.

Исходная математическая модель для волновой функции электронных компонентов 8-компонентного спинора Кейна, локализованных на кольце, в указанных единицах имеет вид

с граничными условиями

Здесь Δ⁽²⁾ – двухмерный лапласиан, В – индукция внешнего однородного магнитного поля, е – элементарный заряд, V(r) – периодический потенциал матричного полупроводника, $\varepsilon $ – энергия связи электрона в кольце. Верхний индекс в фигурных скобках в правой части соответствует области матрицы (как обычно, энергия отсчитывается от дна зоны проводимости матрицы), нижний индекс – области внутри кольца, g* – эффективный фактор Ланде для матричного электрона, ${{\mu }_{B}}$ – магнетон Бора. Последний член в правой части – энергия взаимодействия спина электрона с магнитным полем; верхний знак соответствует направлению спина вдоль поля, нижний – соответственно против. Спин-орбитальным взаимодействием в обоих общепринятых вариантах [5] мы здесь пренебрегаем, ибо на удерживающем потенциале кольца, определяемом радиальными функциями, оно сказывается слабо. Магнитное поле достаточно велико, чтобы влиять на энергию углового движения электрона, но не настолько велико, чтобы квантовать движение электрона в матрице (∼1–10 Тл). В этом случае использовать для волновой функции разложение по уровням Ландау нецелесообразно [8, 9].

После отделения решеточных функций Ванье, локализованных на узлах тонкого кольца (для такого рода ситуаций они удобнее периодических блоховских функций [10]), решения уравнений для вертикальной и угловой составляющих получаем уравнение для гладкой огибающей радиальной волновой функции ${{\psi }_{{nq}}}\left( r \right)$. Оно явно приведено в [7], так что здесь продемонстрируем лишь характер его решения для конкретного примера гетероcтруктуры InAs/AlSb (рис. 1)

где I, J, K – цилиндрические функции соответственно Инфельда, Бесселя и Макдональда, А, В и D – нормировочные постоянные (их значения в дальнейшем не понадобятся), n – номер экстремума функции Бесселя, описывающего волновую функцию внутри кольца, q – “эффективное орбитальное число” в магнитном поле $\Phi = \pi BR_{0}^{2}$ – магнитный поток через кольцо, Φ₀ = = $\frac{{2\pi \hbar }}{e}$ – его квант (с учетом того, что у нас в кольце не куперовская пара 2е, а уединенный электрон).

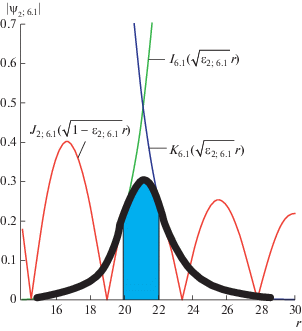
Толщина кольца позволяет “вместить” окрестность только одного такого экстремума. Решение (2) должно удовлетворять трем дополнительным условиям: двум условиям непрерывности логарифмической производной на двух гетерограницах кольца

а также условию того, что экстремум функции Бесселя лежит внутри кольца

Именно сочетание этих условий и формирует селекционные свойства кольца. В отсутствие магнитного поля $\Phi = 0$ индекс функций Бесселя $q = l$, т.е. меняться может лишь дискретно. При этом условия (3), (4) могут согласоваться лишь случайно, при строго определенных значениях ${{R}_{{in}}}$ и ${{R}_{{ex}}}$. Для произвольных геометрических размеров кольца согласование может обеспечить лишь непрерывное изменение q, а это возможно лишь за счет магнитного поля. Разумеется, в нашем случае магнитный поток Φ не кратен ${{\Phi }_{0}}$, как в объемном сверхпроводнике; в кольце условия квантования совсем другие.

Таким образом, устойчивые связанные одноэлектронные состояния формируются в кольце лишь при строго определенных значениях магнитного поля, причем каждый уровень соответствует единственному набору n, l, $ \pm g{\text{*}}$. Это показано на рис. 2 для S- и P-состояний электрона в кольце.

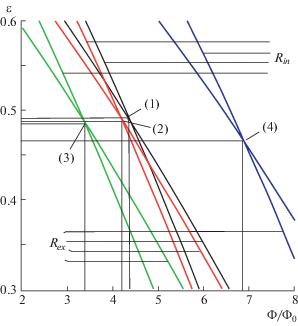
Легко видеть, что если состояние (1) – исходное, то любое его квантовое число мы можем изменить, меняя должным образом магнитное поле. Фактически это – аналог “плоского атома Бора” с полностью управляемыми свойствами.

Коротко остановимся на энергии переходов между состояниями, показанными на рис. 2. Отметим, что трансцендентные условия (3) не дают возможности явно увидеть зависимость энергии состояния от его квантовых чисел и параметров гетероструктуры. Это можно сделать, используя аналитическую аппроксимацию функций Бесселя в (3). В результате для энергии связанного уровня получаем хоть и весьма приближенное, но качественно понятное выражение

где $d = {{R}_{{ex}}} - {{R}_{{in}}}$ – ширина кольца в единицах r₀, последнее слагаемое – энергия вертикального движения (${{q}_{z}}$ – волновое число в z-компоненте волновой функции в (1), ∼cos(${{q}_{z}}z$) и зависящее от ΔE_c и толщины кольца по оси z). Вертикальную толщину кольца всегда можно сделать столь малой, чтобы возбуждался только минимальный уровень вертикального движения. Меняется при переходах, таким образом, только параметр q, связанный с магнитным полем. При переходе из состояния (1) в состояние (2) меняется лишь ориентация спина, так что энергия кванта определяется соотношением:

Существенно, что такие переходы лежат в терагерцевом диапазоне [12] и теоретически могут быть использованы для прямой генерации ТГц-излучения с перестраиваемой частотой. Переход из (1) в (3), сопровождающийся изменением орбитального момента на 1, дает энергию кванта

где значения $\frac{{{{\Phi }_{1}}}}{{{{\Phi }_{0}}}}$ и $\frac{{{{\Phi }_{2}}}}{{{{\Phi }_{0}}}}$ можно оценить по рис. 2. Такие переходы значительно больше первых по энергии. Самые высокоэнергетические переходы внутри кольца типа (1)–(4) связаны с изменением номера экстремума функции Бесселя n. Они описываются предыдущим выражением, но магнитный поток, как видно из рис. 2, меняется значительно существеннее. Таким образом, энергия кванта формируется почти исключительно из энергии магнитного поля.

В оптическом (а возможно, и ультрафиолетовом) диапазоне лежат переходы из зоны проводимости матрицы на (единственный) уровень кольца. Остановимся на них чуть подробнее в силу их, возможно уникальной, эффективности. Пусть в начальном состоянии магнитное поле выключено и уровни в кольцах “закрыты”. Включая магнитное поле нужной величины, мы эти уровни “открываем”, и электроны со дна зоны проводимости будут переходить на них, излучая, как можно показать, направленные и близкие к монохроматическим кванты (вопрос о когерентности, необходимой для лазерной генерации, мы сейчас даже не ставим). После обратного выключения поля электроны, локализованные на кольцах, будут терять устойчивость и вытесняться обратно в зону проводимости (либо в валентную зону) за счет энергии тепловых фононов. Напомним, что кольцо тонкое и электроны, даже локализованные на кольце, большую часть времени проводят в матрице (см. рис. 1). В итоге последовательность прямоугольных импульсов магнитного поля необходимой величины фактически преобразует тепловую энергию электронов в высокосортную энергию монохроматического излучения. Разумеется, второму закону термодинамики это не противоречит, так как и переключение магнитного поля требует затрат энергии для достижения порогового условия генерации.

В заключение отметим, что, кроме эффективности, квантовые кольца как активные элементы обладают целым рядом преимуществ по сравнению с квантовыми точками. Связано это прежде всего с тремя факторами: 1) более жесткими правилами отбора, обеспечивающими более чистый энергетический спектр; 2) цилиндрической симметрией колец, ориентирующей излучаемые кванты вдоль оси симметрии и 3) главное преимущество – возможность перестройки частоты излучения простым переключением магнитного поля.