Доклады Российской академии наук. Физика, технические науки, 2021, T. 501, № 1, стр. 23-28

ВВЕДЕНИЕ

В научной литературе открытым остается вопрос о достоверности “гипотезы единой кривой” при больших деформациях из-за сложностей экспериментального анализа неоднородного НДС. Экспериментально установлено, что некоторые материалы обладают зависимостью пластических свойств от вида напряженного состояния [1–4]. В теоретических исследованиях при описании процессов деформирования и разрушения таких материалов физические соотношения дополняются зависимостями от параметров вида напряженного состояния, выраженных через главные напряжения [5–7]: параметр “жесткости” напряженного состояния (параметр трехосности напряжений), параметр вида напряженного состояния, параметр Надаи–Лоде по напряжениям и другие.

При построении истинных диаграмм деформирования в условиях больших деформаций и неоднородного НДС применяются итерационные экспериментально-расчетные методы [8–11]. Они основаны на итерационной процедуре корректировки зависимости интенсивности напряжений от интенсивности деформаций пропорционально относительному различию значений осевых сил, полученных в расчете и эксперименте при неоднородном НДС с учетом образования шейки до разрыва. При таком подходе необходимо многократно решить прямую задачу с итерационно уточняемыми механическими характеристиками. Авторами [1] разработана оригинальная методика решения обобщенной задачи кручения в двумерной постановке. В современных пакетах программ задачи кручения тел вращения и задачи осесимметричного нагружения с кручением можно решать только в трехмерной постановке, что является трудоемкой вычислительной задачей.

В работе представлен новый эффективный алгоритм построения истинной диаграммы деформирования с разбивкой всего процесса нагружения на интервалы, определяемые дискретными значениями экспериментальной зависимости обобщенной силы от обобщенного перемещения. В ходе вычисления в конце каждого интервала разбиения анализируется отличие расчетной обобщенной силы от экспериментальной и, при превышении заданной погрешности, выполняется итерационная корректировка величины интенсивности напряжений на границе текущего интервала истинной диаграммы деформирования. Для продолжения прямого расчета на следующем интервале разбиения применятся процедура нелинейной экстраполяции диаграммы деформирования, которая существенно повышает эффективность (до 10 раз) ранее разработанных алгоритмов [8] построения диаграмм деформирования упругопластических материалов. Построены истинные диаграммы деформирования конструкционных низколегированных сталей 10ХСНД и 10Г2ФБЮ, выявлена их зависимость от вида напряженного состояния при умеренных и больших деформациях.

АЛГОРИТМ ПОСТРОЕНИЯ ДИАГРАММ ДЕФОРМИРОВАНИЯ

Процесс нагружения разбивается на малые этапы. Количество этапов $N$ равно количеству точек в табличном представлении экспериментальной зависимости обобщенной силы от обобщенного перемещения. Столько же точек будет содержать построенная истинная диаграмма деформирования (зависимость интенсивности напряжений $\sigma _{i}^{{}}$ от параметра Одквиста $\kappa $). В конце каждого этапа $n$ ($n = 1, \ldots ,N$) анализируется величина отклонения расчетной обобщенной силы $F_{Р}^{n}$ от экспериментальной $F_{{\text{Э}}}^{n}$. При превышении заданной погрешности производится итерационная корректировка интенсивности напряжений по формулам: $\sigma _{i}^{n}({{\kappa }^{n}}) = \beta \bar {\sigma }_{i}^{n}({{\kappa }^{n}})$, $\beta = F_{{\text{Э}}}^{n}{\text{/}}F_{P}^{n}$, причем ${{\kappa }^{n}}$ соответствует параметру Одквиста в конце этапа $n$. При достижении необходимой точности в таблицу истинной диаграммы деформирования заносится новая точка $\sigma _{i}^{n}({{\kappa }^{n}})$ и выполняется переход на следующий этап $n + 1$. Для этого осуществляется процедура нелинейной экстраполяции с использованием $m$ последних точек построенного участка диаграммы деформирования. Необходимо иметь не менее трех опорных точек ($m \geqslant 3$). Сначала выполняется процедура экстраполяции безразмерного параметра [9] $K\left( \kappa \right) = \frac{1}{{{{\sigma }_{i}}(\kappa )}}\frac{{d{{\sigma }_{i}}(\kappa )}}{{d\kappa }}$ в виде степенной функции методом наименьших квадратов. Затем вычисляются экстраполяционные значения опорных точек диаграммы деформирования при $\kappa \geqslant {{\kappa }^{n}}$ по формуле ${{\sigma }_{i}}\left( \kappa \right) = {{\sigma }_{i}}({{\kappa }^{n}})\exp \left( {\int\limits_{{{\kappa }^{n}}}^\kappa {Kd\kappa } } \right)$. Для этапов нагружения $n < m$ принимается $m = n$. Начальный участок истинной диаграммы деформирования, включающий первые три этапа нагружения ($n = 1, \ldots ,3$), определяется на основе итерационной процедуры [8] без экстраполяции. Отметим, что диаграммы деформирования являются монотонно возрастающими функциями с убывающей производной, что позволяет с высокой точностью определить начальное приближение диаграммы для последующих этапов нагружения.

Максимальная эффективность предложенного алгоритма достигается в случае, когда количество точек экстраполяции $m$ составляет около 12% от общего количества точек $N$, аппроксимирующих диаграмму. С увеличением количества этапов (точек, аппроксимирующих диаграмму) итерационная процедура построения диаграммы деформирования практически сводится к однократному прямому численному расчету без применения итерационной процедуры, что существенно повышает эффективность (до 10 раз) методик [8] построения диаграммы деформирования упругопластических материалов.

ТЕОРЕТИЧЕСКОЕ И ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ПРОЦЕССОВ ДЕФОРМИРОВАНИЯ СТЕРЖНЕЙ ПРИ РАСТЯЖЕНИИ-КРУЧЕНИИ И ПОСТРОЕНИЕ ИСТИННЫХ ДИАГРАММ ДЕФОРМИРОВАНИЯ

Проведено экспериментальное и численное исследование процессов деформирования осесимметричных образцов переменной толщины с цилиндрической рабочей частью из стали 10Г2ФБЮ при монотонном кинематическом нагружении растяжением-кручением с учетом больших деформаций и неоднородности НДС.

Для построения истинных диаграмм деформирования проводился эксперимент на испытательном комплексе Z100 ZWICK-ROEL, предназначенном для испытаний на растяжение и кручение цилиндрических образцов при одновременном синхронизированном по времени задании параметров: скорость изменения продольного перемещения – скорость изменения угла закручивания. Испытания проводились на сплошных цилиндрических образцах с размерами: начальный радиус рабочей части ${{R}_{0}} = 6$ мм, первоначальная длина рабочей частей ${{L}_{0}} = 60$ мм.

Полная система уравнений [1], описывающих решение обобщенных двумерных задач кручения, записывается в цилиндрической системе координат $Orz\beta $ ($Oz$ – ось вращения). Уравнение движения сплошной среды следует из уравнения баланса виртуальных мощностей. Кинематические соотношения формулируются в скоростях и строятся в метрике текущего состояния, что позволяет учитывать большие формоизменения. Упругопластические свойства материалов описываются теорией течения с нелинейным изотропным упрочнением, поскольку рассматриваются процессы активного нагружения, близкие к пропорциональным. Для численного моделирования процессов деформирования образцов при пропорциональном комбинированном нагружении растяжением-кручением реализована зависимость диаграммы деформирования от вида напряженного состояния. Уточненная диаграмма деформирования является линейной комбинацией диаграмм растяжения $\sigma _{i}^{{{\text{ten}}}} = \sigma _{i}^{{{\text{ten}}}}\left( \kappa \right)$ и кручения $\sigma _{i}^{{{\text{tor}}}} = \sigma _{i}^{{{\text{tor}}}}\left( \kappa \right)$, коэффициенты которой зависят от параметра вида напряженного состояния $П$ [6]:

Начально-краевая задача решается по явной конечно-разностной схеме интегрирования по времени типа “крест” [1]. Темп нагружения задавали таким образом, чтобы вклад инерционных сил был пренебрежимо мал. Разработанная методика численного решения реализована на базе пакета прикладных программ “Динамика-2” [12].

На основе проведенных экспериментов по кручению и растяжению с применением предложенного алгоритма, построены истинные диаграммы деформирования для сталей 12Х18Н10Т, 09Г2С, 10ХСНД и 10Г2ФБЮ (рис. 1, кривые 1–4 соответственно). На рис. 1 сплошными линиями отмечены истинные диаграммы деформирования, построенные из экспериментальных данных по монотонному кручению до разрушения образца, штриховыми – по одноосному растяжению с учетом образования шейки.

Рис. 1.

Истинные диаграммы деформирования сталей 12Х18Н10Т (1), 09Г2С (2), 10ХСНД (3) и 10Г2ФБЮ (4) при растяжении (пунктирные линии) и кручении (сплошные линии).

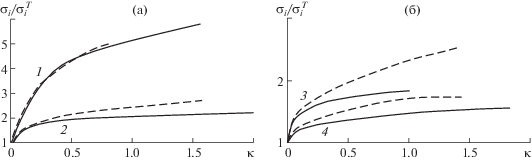
Для стали 12Х18Н10Т “гипотеза единой кривой” подтверждается при больших деформациях, поскольку диаграммы деформирования при кручении и растяжении образцов из этого материала практически совпали при деформациях до 80% (рис. 1, кривые 1). Это согласуется с результатами исследования [10]. Для сталей 09Г2С и 10ХСНД “гипотеза единой кривой” выполняется при деформациях до 15 и 4% соответственно, и не выполняется при больших деформациях. Диаграммы растяжения и кручения стали 10Г2ФБЮ (рис. 1, кривые 4), построенные при двух видах нагружения, отличаются друг от друга на всем интервале деформирования. При величине параметра Од-квиста $\kappa $ = 0.09 (момент начала образования шейки при одноосном растяжении) расхождение между кривыми составляет 4%, при $\kappa $ = 1–16%.

В испытаниях сталей 12Х18Н10Т, 09Г2С и 10Г2ФБЮ максимальное значение параметра Одквиста до разрушения достигается при кручении. Для стали 12Х18Н10Т оно вдвое выше, чем при растяжении, а для сталей 09Г2С и 10Г2ФБЮ больше на 20%. Для стали 10ХСНД максимальное значение параметра Одквиста достигается при растяжении (в шейке), оно на 40% больше, чем при кручении.

Введем необходимые для дальнейшего анализа обозначения параметров задачи:

угол закручивания по окружной координате и осевое перемещение подвижного торца образца: $\theta $ и ${{u}_{z}}$;

кинематический параметр, характеризующий соотношение кручения и растяжения, при пропорциональном нагружении $q \equiv {\text{const}}$:

$q = \frac{{{{R}_{0}}\theta }}{{\sqrt 3 {{u}_{z}}}}$;

условная интенсивность деформации на поверхности рабочей части образца:

${{\bar {e}}_{i}} = \sqrt {\bar {e}_{{zz}}^{2} + \frac{4}{3}\bar {e}_{{\beta z}}^{2}} $ = $\frac{{{{u}_{z}}}}{{{{L}_{0}}}}\sqrt {1 + {{q}^{2}}} $;

условная осевая деформация:

${{\bar {e}}_{{zz}}} = \frac{{{{u}_{z}}}}{{{{L}_{0}}}}$;

условная сдвиговая деформация на поверхности рабочей части образца:

${{\bar {e}}_{{\beta z}}} = \frac{1}{2}\frac{{{{R}_{0}}\theta }}{{{{L}_{0}}}}$;

осевая сила и крутящий момент:

F = $2\pi \int\limits_0^R {{{\sigma }_{{z{\kern 1pt} z}}}rdr} $ и $M = 2\pi \int\limits_0^R {{{\sigma }_{{\beta {\kern 1pt} z}}}{{r}^{2}}dr} $;

обобщенная осевая сила:

$W({{\bar {e}}_{i}})$ = $\frac{{{{L}_{0}}}}{{\sqrt {1 + {{q}^{2}}} }}\left( {F + M\frac{{\sqrt 3 q}}{{{{R}_{1}}}}} \right)$;

суммарная работа осевой силы и крутящего момента:

A = $\int\limits_0^{{{u}_{z}}} {Fd{{u}_{z}}} \, + \,\int\limits_0^\theta {Md\theta } $ = $\int\limits_0^{{{{\bar {e}}}_{i}}} {\frac{{{{L}_{0}}}}{{\sqrt {1\, + \,{{q}^{2}}} }}\left( {F\, + \,\frac{{\sqrt 3 q}}{{{{R}_{1}}}}M} \right)d} {{\bar {e}}_{i}}$ = = $\int\limits_0^{{{{\bar {e}}}_{i}}} {Wd} {{\bar {e}}_{i}}$.

В качестве критерия потери устойчивости пластического деформирования с образованием шейки при пропорциональном нагружении растяжением-кручением принимается условие $\frac{{dW}}{{d{{{\bar {e}}}_{i}}}}$ = 0 [1], характеризующее момент достижения обобщенной силой W максимальных значений. Данный критерий является обобщением известного условия А. Консидера, полученного при растяжении стержней [13].

На рис. 2 приведены экспериментальные (сплошные линии) и расчетные (штриховые линии) зависимости осевой силы от условной осевой деформации $F = F\left( {{{{\bar {e}}}_{{zz}}}} \right)$ и крутящего момента от условной сдвиговой деформации на поверхности рабочей части образца $M = M\left( {{{{\bar {e}}}_{{\beta z}}}} \right)$ для образца из стали 10Г2ФБЮ. Соответствующие значения параметра $q$ приведены рядом с кривыми. При чистом кручении и одноосном растяжении экспериментальные и расчетные кривые практически совпадают и приведены сплошными линиями. Точками отмечены моменты потери устойчивости пластического деформирования с образованием шейки, которым соответствуют максимальные значения обобщенной силы W. Расчетные зависимости хорошо согласуются с экспериментальными данными как по величине, так и по моменту достижения максимальных значений интегральных характеристик – сил F и моментов M.

Рис. 2.

Экспериментальные и расчетные зависимости осевой силы от условной осевой деформации и крутящего момента от условной сдвиговой деформации на поверхности рабочей части образца из стали 10Г2ФБЮ.

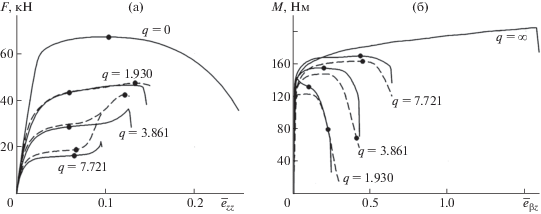
При комбинированном нагружении растяжением-кручением в эксперименте и расчете после момента потери устойчивости в процессе образования шейки, в отличие от одноосного растяжения, наблюдается более интенсивный рост осевой силы F до разрушения, при этом величина крутящего момента M уменьшается из-за уменьшения радиуса поперечного сечения шейки. При чистом растяжении нисходящая ветвь экспериментальной кривой расчетом описывается также удовлетворительно. При наложении кручения на растяжение и чистом кручении эта ветвь не описывается, поскольку при численном моделировании не были учтены поврежденность материала и разрушение, которое имеет многостадийный характер, включающий в себя образование микроповреждений, слияние микропор, а затем развитие макроразрушения. Процесс макроразрушения начинается на поверхности образца и при дальнейшем нагружении (кручении) распространяется к оси вращения.

Процессы деформирования до момента потери устойчивости близки к лучевым, а закритическое поведение характеризуется траекториями малой кривизны. При комбинированном нагружении до момента потери устойчивости во всем объеме образца вид напряженного состояния медленно изменяется в сторону растяжения, так как образец утончается. Изменение вида напряженного состояния в шейке в сторону деформации чистого сдвига после момента потери устойчивости происходит наиболее интенсивно при одноосном растяжении. До момента падения осевой силы во всем объеме образца происходит процесс активного нагружения. В месте образования шейки активный процесс продолжается до разрушения. В экспериментах шейка образуется в средней части образца, ее положение зависит от многих случайных факторов. В расчетах образование шейки происходит на плоскости симметрии.

ЗАКЛЮЧЕНИЕ

Разработан эффективный алгоритм построения истинной диаграммы деформирования с разбивкой всего процесса нагружения на интервалы, определяемые дискретными значениями экспериментальной зависимости обобщенной силы от обобщенного перемещения. В ходе вычисления в конце каждого интервала разбиения анализируется отличие расчетной обобщенной силы от экспериментальной и, при превышении заданной погрешности, выполняется итерационная корректировка величины интенсивности напряжений на границе текущего интервала истинной диаграммы деформирования. Для продолжения прямого расчета на следующем интервале разбиения применятся процедура нелинейной экстраполяции диаграммы деформирования. Построены истинные диаграммы деформирования конструкционных низколегированных сталей 10ХСНД и 10Г2ФБЮ. Выявлена их зависимость от вида напряженного состояния при умеренных и больших деформациях, что позволило существенно уточнить результаты численного моделирования процессов упругопластического деформирования стержней при комбинированных нагружениях растяжением-кручением.

Реализована оригинальная методика численного решения обобщенной задачи кручения (осесимметричное деформирование и кручение) упругопластических тел вращения с учетом больших деформаций и неоднородности НДС в двумерной постановке [1]. Современные вычислительные комплексы позволяют решать задачи кручения и задачи осесимметричного нагружения с кручением тел вращения только в трехмерной постановке. Большие сдвиговые деформации приводят к существенному искажению конечно-элементной сетки, что требует ее многократного перестроения в ходе решения и снижает точность расчетов. Время счета одной прямой задачи комбинированного пропорционального нагружения растяжением-кручением осесимметричных образцов в двумерной постановке на процессоре с тактовой частотой 4.4 ГГц на разностной сетке 20 × 150 узлов составляет порядка 5 мин. Аналогичный расчет в трехмерной постановке является на два-три порядка более трудоемкой вычислительной задачей и возникает необходимость в использовании кластера с большим числом ядер.