Доклады Российской академии наук. Физика, технические науки, 2022, T. 503, № 1, стр. 52-56

ОБ ИСПОЛЬЗОВАНИИ НЕСКОЛЬКИХ ПОДВИЖНЫХ МАСС ДЛЯ ПЕРЕОРИЕНТАЦИИ ТЕЛА

Академик РАН Ф. Л. Черноусько^1, *

¹ Институт проблем механики им. А.Ю. Ишлинского Российской академии наук
Москва, Россия

Поступила в редакцию 14.12.2021
После доработки 14.12.2021
Принята к публикации 18.02.2022

EDN: WGBTED
DOI: 10.31857/S268674002202002X

Аннотация

Предложен новый способ управления ориентацией твердого тела при помощи нескольких вспомогательных масс, движущихся относительно тела. Заданная переориентация достигается путем трех плоских поворотов, в каждом из которых движется одна масса. Алгоритм допускает значительную свободу размещения подвижных масс в теле.

Ключевые слова: динамика твердого тела, управление движением, ориентация

Подвижные массы, расположенные внутри твердого тела, могут использоваться для изменения его ориентации в пространстве. Плоские движения таких систем, управляемых при помощи вспомогательных внутренних масс, рассматривались в ряде работ в связи с управлением мобильными капсульными роботами [1–5]. Если мобильный робот с внутренними подвижными массами совершает быстрый поворот относительно центра масс, то в ряде случаев влиянием внешних сил и моментов за время поворота можно пренебречь и считать, что на систему не действуют внешние силы и моменты. Это происходит, если силы взаимодействия корпуса робота и подвижных внутренних масс значительно превосходят внешние силы. Такая ситуация может иметь место также для поворотов космических аппаратов и других подвижных объектов.

При отсутствии внешних сил уравнения движения системы значительно упрощаются, что дает возможность построить оптимальные алгоритмы поворота и в явном виде получить оптимальные траектории [6, 7]. В важном случае, когда внутренняя масса мала по сравнению с массой несущего тела [6], оптимальная траектория подвижной массы в случае плоского поворота оказывается дугой окружности. Алгоритм пространственной переориентации тела при помощи одной подвижной массы, предложенный в работe [8] на основе оптимальных плоских поворотов, предполагает движение этой массы в окрестности центра масс несущего тела, что может быть неудобно по конструктивным соображениям. В работe [9] предложено использовать несколько подвижных масс для управления ориентацией тела. Показано, что при этом имеется большая свобода выбора областей, в которых движутся внутренние массы, но требуется синхронизация движений этих масс. В данной работе также используется несколько подвижных масс и сохраняется значительная свобода выбора по их размещению в теле. Однако предлагаемый ниже алгоритм переориентации не требует синхронизации движения, так как здесь всегда движется только одна из внутренних масс.

ОСНОВНЫЕ УРАВНЕНИЯ

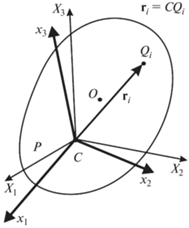
Рассматриваемая механическая система состоит из твердого тела Р массы M и n материальных точек ${{Q}_{i}}$ массы ${{m}_{i}},i = 1,...,n.$ Точки ${{Q}_{i}}$ могут двигаться относительно тела Р под действием двигателей (актюаторов), взаимодействуя с телом Р, но не с внешней средой. Внешние силы, действующие на систему, считаем пренебрежимо малыми. Обозначим через С центр масс тела Р, а через О – центр масс всей системы. Предполагаем, что в начальный момент $t = 0$ система покоится. Тогда ее центр масс О неподвижен и может быть принят в качестве начала координат неподвижной системы $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$. Введем также систему координат $C{{x}_{1}}{{x}_{2}}{{x}_{3}}$, связанную с телом Р, и обозначим через ${{{\mathbf{r}}}_{i}} = C{{Q}_{i}}$ радиус-вектор подвижной точки ${{Q}_{i}}$ в системе координат $C{{x}_{1}}{{x}_{2}}{{x}_{3}}$ (см. рис. 1).

Рис. 1.

Механическая система.

Скорость точки ${{Q}_{i}}$ относительно системы координат $C{{x}_{1}}{{x}_{2}}{{x}_{3}}$ будем обозначать через ${{\dot {r}}_{i}}$. Тогда, как показано в работе [9] на основе законов сохранения импульса и кинетического момента всей системы, справедливо следующее уравнение:

(1)

$\begin{gathered} {\mathbf{J}} \cdot \omega - {{\left( {M + m} \right)}^{{ - 1}}}\left( {\sum\limits_{i = 1}^n {{{m}_{i}}} {{{\mathbf{r}}}_{i}}} \right) \times \\ \; \times \left[ {\sum\limits_{i = 1}^n {{{m}_{i}}} \left( {\omega \times {{{\mathbf{r}}}_{i}} + {{{{\mathbf{\dot {r}}}}}_{i}}} \right)} \right] + \sum\limits_{i = 1}^n {{{m}_{i}}} {{{\mathbf{r}}}_{i}} \times \left( {\omega \times {{{\mathbf{r}}}_{i}} + {{{{\mathbf{\dot {r}}}}}_{i}}} \right) = 0. \\ \end{gathered} $

Здесь ω – угловая скорость тела Р, J – тензор инерции тела Р относительно его центра масс С и введено обозначение

(2)

$m = \sum\limits_{i = 1}^n {{{m}_{i}}} .$

Уравнение (1) связывает угловую скорость ω тела Р с характеристиками движения точек Q_i относительно этого тела – их положениями r_i и скоростями ${{\dot {r}}_{i}},{\text{ }}i = 1,...,n$.

ОТНОСИТЕЛЬНЫЕ ДВИЖЕНИЯ

Представим векторы ${{{\mathbf{r}}}_{i}}(t)$ в виде

(3)

${{{\mathbf{r}}}_{i}}(t) = {\mathbf{r}}_{i}^{0} + {{\rho }_{i}}(t),\quad i = 1,...,n,$

где ${\mathbf{r}}_{i}^{0}$ – постоянные векторы, задающие положения точек Q_i в начальный момент t = 0:

(4)

$r_{i}^{0} = {{r}_{i}}(0),\quad i = 1,...,n,$

а векторы ${{\rho }_{i}}$ определяют смещения точек Q_i из начального состояния. Обозначим через $Q_{i}^{0}$ материальные точки массы m_i, находящиеся постоянно в начальном состоянии, т.е. при ${{\rho }_{i}} = 0$.

Наложим следующее условие на векторы ${\mathbf{r}}_{i}^{0}$:

(5)

$\sum\limits_{i = 1}^n {{{m}_{i}}} {\mathbf{r}}_{i}^{0} = 0,$

означающее, что центр масс совокупности всех точек $Q_{i}^{0},{\text{ }}i = 1,...,n$, находится в центре масс С тела Р. Эту совокупность обозначим через Q⁰; ее можно рассматривать как твердое тело массы m, определенной равенством (2), с центром масс в точке С.

Подставим соотношения (3) в уравнение (1) и преобразуем полученное уравнение, используя равенство (5). Получим

(6)

$\begin{gathered} {\mathbf{J}} \cdot \omega - {{\left( {M + m} \right)}^{{ - 1}}}\left( {\sum\limits_{i = 1}^n {{{m}_{i}}} {{\rho }_{i}}} \right) \times \\ \, \times \left[ {\sum\limits_{i = 1}^n {{{m}_{i}}} \left( {\omega {{ \times }_{i}}\rho + {{{\dot {\rho }}}_{i}}} \right)} \right] + \sum\limits_{i = 1}^n {{{m}_{i}}} {\mathbf{r}}_{i}^{0} \times (\omega \times {\mathbf{r}}_{i}^{0}) + \\ \, + \sum\limits_{i = 1}^n {{{m}_{i}}} [{\mathbf{r}}_{i}^{0} \times \left( {\omega \times {{\rho }_{i}}} \right) + r_{i}^{0} \times {{{\dot {\rho }}}_{i}} + {{\rho }_{i}} \times (\omega \times {\mathbf{r}}_{i}^{0})] + \\ \, + \sum\limits_{i = 1}^n {{{m}_{i}}} {{\rho }_{i}} \times \left( {\omega \times {{\rho }_{i}} + {{{\dot {\rho }}}_{i}}} \right) = 0. \\ \end{gathered} $

Третье слагаемое в уравнении (6) представляет собой кинетический момент виртуального твердого тела ${{Q}^{0}}$ относительно его центра масс С и может быть записано в виде

(7)

$\sum\limits_{i = 1}^n {{{m}_{i}}} {\mathbf{r}}_{i}^{0} \times (\omega \times {\mathbf{r}}_{i}^{0}) = {{{\mathbf{J}}}^{0}} \cdot \omega ,$

где J⁰ – тензор инерции твердого тела ${{Q}^{0}}$ относительно его центра масс С.

Обозначим через J* тензор инерции твердого тела $P + {{Q}^{0}}$, состоящего из тел Р и ${{Q}^{0}}$, относительно их общего центра масс С:

(8)

${\mathbf{J}}{\kern 1pt} * = {\mathbf{J}} + {{{\mathbf{J}}}^{0}}.$

Принимая во внимание уравнения (7) и (8), перепишем уравнение (6) в виде

(9)

$\begin{gathered} {\mathbf{J}}{\kern 1pt} * \cdot \,\omega - {{\left( {M + m} \right)}^{{ - 1}}}\left( {\sum\limits_{i = 1}^n {{{m}_{i}}} {{\rho }_{i}}} \right) \times \left[ {\sum\limits_{i = 1}^n {{{m}_{i}}} \left( {\omega \times {{\rho }_{i}} + {{{\dot {\rho }}}_{i}}} \right)} \right] + \\ \, + \sum\limits_{i = 1}^n {{{m}_{i}}} [2\omega ({\mathbf{r}}_{i}^{0}{{\rho }_{i}}) - {{\rho }_{i}}(\omega {\mathbf{r}}_{i}^{0}) - {\mathbf{r}}_{i}^{0}\left( {\omega {{\rho }_{i}}} \right) + r_{i}^{0} \times {{{\dot {\rho }}}_{i}}] + \\ \, + \sum\limits_{i = 1}^n {{{m}_{i}}} {{\rho }_{i}} \times \left( {\omega \times {{\rho }_{i}} + {{{\dot {\rho }}}_{i}}} \right) = 0. \\ \end{gathered} $

ЗАДАЧА ПЕРЕОРИЕНТАЦИИ

В начальный момент t = 0 система, состоящая из тела Р и материальных точек ${{Q}_{i}},i = 1,...,n$, находится в покое. Требуется, при помощи движений точек Q_i, осуществить в некоторый (нефиксированный) момент времени Т заданную конечную ориентацию тела Р в пространстве. В этот момент Т тело Р и точки ${{Q}_{i}},\,\,i = 1,...,n$, должны находиться в состоянии покоя, причем все точки ${{Q}_{i}}$ должны вернуться в начальное положение относительно тела Р. Таким образом, должны быть выполнены краевые условия

(10)

$\begin{gathered} \omega (0) = \omega (T) = 0,\quad {{\rho }_{i}}(0) = {{\rho }_{i}}(T) = 0, \\ {{{\dot {\rho }}}_{i}}(0) = {{{\dot {\rho }}}_{i}}(T) = 0,\quad i = 1,...,n. \\ \end{gathered} $

Направим оси системы координат $C{{x}_{1}}{{x}_{2}}{{x}_{3}}$ вдоль главных центральных осей инерции твердого тела $P + {{Q}^{0}}$. Требуемая переориентация может быть осуществлена путем трех последовательных плоских поворотов тела вокруг осей $C{{x}_{i}},i = 1,2,3$. Обозначим через ${{{\mathbf{e}}}_{i}}$ орты этих осей. Потребуем, чтобы для каждого из этих поворотов выполнялись краевые условия (10). Тогда все повороты можно рассматривать аналогичным образом. Для определенности рассмотрим поворот вокруг оси $C{{x}_{3}}$.

ПЛОСКИЙ ПОВОРОТ

В работе [9] предлагается выбирать векторы ${{\rho }_{i}}$ в (3) одинаковыми и полагать ${{\rho }_{i}}(t) = \rho (t)$, i = 1, ..., n. При этом имеется большая свобода в размещении подвижных точек ${{Q}_{i}}$ внутри тела Р, однако, ввиду равенств ${{\rho }_{i}}(t) = \rho (t)$, необходимо осуществить синхронизацию движений этих точек.

Рассмотрим здесь другую возможность, при которой только одна из масс ${{Q}_{i}}$ всегда находится в движении. Положим

(11)

${{\rho }_{k}}(t) \ne 0,\quad {{\rho }_{i}}(t) = 0,\quad i \ne k,\quad i = 1,...,n.$

Подставляя соотношения (11) в уравнение (9), получим

(12)

$\begin{gathered} {\mathbf{J}}{\kern 1pt} * \cdot \,\omega - {{\left( {M + m} \right)}^{{ - 1}}}m_{k}^{2}{{\rho }_{k}} \times \left( {\omega \times {{\rho }_{k}} + {{{\dot {\rho }}}_{k}}} \right) + \\ + \,{{m}_{k}}[2\omega ({\mathbf{r}}_{k}^{0}{{\rho }_{k}}) - {{\rho }_{k}}(\omega {\mathbf{r}}_{k}^{0}) - {\mathbf{r}}_{k}^{0}\left( {\omega {{\rho }_{k}}} \right) + r_{k}^{0} \times {{{\dot {\rho }}}_{k}}] + \\ + \,{{m}_{k}}{{\rho }_{k}} \times \left( {\omega \times {{\rho }_{k}} + {{{\dot {\rho }}}_{k}}} \right) = 0. \\ \end{gathered} $

Рассматривая плоский поворот вокруг оси $C{{x}_{3}}$, положим, что точка $Q_{k}^{0}$ лежит в плоскости $C{{x}_{1}}{{x}_{2}}$. Тогда вектор ${\mathbf{r}}_{k}^{0}$ можно представить в виде

(13)

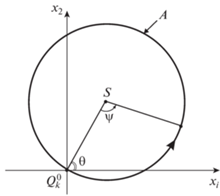
${\mathbf{r}}_{k}^{0} = r_{k}^{0}\left( {\cos {{\beta }_{k}}{{{\mathbf{e}}}_{1}} + \sin {{\beta }_{k}}{{{\mathbf{e}}}_{2}}} \right),$

где $r_{k}^{0}$ – длина вектора, а ${{\beta }_{k}}$ – угол его ориентации в плоскости $C{{x}_{1}}{{x}_{2}}$.

Как показано в [6], оптимальными по быстродействию траекториями подвижной массы в важном случае, когда эта масса мала по сравнению с массой тела, являются дуги окружностей. Согласно краевым условиям (10), следует выбрать траекторию вектора ${{\rho }_{k}}(t)$ в виде замкнутой окружности А радиуса а, проходящей через точку $Q_{k}^{0}$ в плоскости $C{{x}_{1}}{{x}_{2}}$ (рис. 2).

Рис. 2.

Плоский поворот.

Определим координаты центра S окружности А формулами

(14)

$x_{1}^{S} = a\cos \theta ,\quad x_{2}^{S} = a\sin \theta ,\quad x_{3}^{S} = 0.$

Здесь а и $\theta $ – произвольные постоянные. Движение вектора ${{\rho }_{k}}$ по окружности А зададим в виде

(15)

$\begin{gathered} {{\rho }_{k}} = a\left[ {\cos \theta - \cos \left( {\theta + \psi } \right)} \right]{{{\mathbf{e}}}_{1}} + \\ \; + a\left[ {\sin \theta - \sin \left( {\theta + \psi } \right)} \right]{{{\mathbf{e}}}_{2}}, \\ \end{gathered} $

где $\psi $ – угол, определяющий положение конца вектора ${{\rho }_{k}}$ на окружности А (рис. 2). Дифференцируя равенство (15), получим

(16)

${{\dot {\rho }}_{k}} = a\dot {\psi }\left[ {\sin \left( {\theta + \psi } \right){{{\mathbf{e}}}_{1}} - \cos \left( {\theta + \psi } \right){{{\mathbf{e}}}_{2}}} \right].$

При плоском вращении тела $P + {{Q}^{0}}$ вокруг оси $C{{x}_{3}}$, которая является главной центральной осью этого тела, имеем

(17)

$\omega = \omega {{{\mathbf{e}}}_{3}},\quad {\mathbf{J}}{\kern 1pt} {\text{*}} \cdot \omega = I\omega {{{\mathbf{e}}}_{3}},\quad \omega = \dot {\varphi },$

где I – момент инерции тела $P + {{Q}^{0}}$ вокруг оси $C{{x}_{3}}$, $\varphi $ – угол поворота этого тела.

Подставим векторы $r_{k}^{0}$, ${{\rho }_{k}}$ и ${{\dot {\rho }}_{k}}$ из соотношений (13), (15), (16) в уравнение (12). Заметим, что справедливы равенства $\omega {\mathbf{r}}_{k}^{0} = \omega {{\rho }_{k}} = 0$ и все векторы в уравнении (12) коллинеарны ${{{\mathbf{e}}}_{3}}$. Поэтому данное уравнение сводится к скалярному уравнению

(18)

$\begin{gathered} I\dot {\varphi } + {{m}_{k}}\left( {1 - \frac{{{{m}_{k}}}}{{M + m}}} \right){{a}^{2}}\left( {2\dot {\varphi } + \dot {\psi }} \right)\left( {1 - \cos \psi } \right) + \\ \; + 2{{m}_{k}}ar_{k}^{0}\dot {\varphi }\left[ {\cos \left( {\theta - {{\beta }_{k}}} \right) - \cos \left( {\theta + \psi - {{\beta }_{k}}} \right)} \right] - \\ \; - {{m}_{k}}ar_{k}^{0}\dot {\psi }\cos \left( {\theta + \psi - {{\beta }_{k}}} \right) = 0. \\ \end{gathered} $

Угол θ, определяющий согласно (14) положение окружности А (см. рис. 2), произволен, и можно принять $\theta = {{\beta }_{k}}$. Тогда уравнение (18) можно записать в виде

(19)

$\begin{gathered} I\dot {\varphi } + {{m}_{k}}\nu {{a}^{2}}(2\dot {\varphi } + \dot {\psi })(1 - \cos \psi ) + \\ \, + {{m}_{k}}ar_{k}^{0}\left[ {2\dot {\varphi }\left( {1 - \cos \psi } \right) - \dot {\psi }\cos \psi } \right] = 0, \\ \end{gathered} $

где введено обозначение

(20)

$\nu = \frac{{M + m - {{m}_{k}}}}{{M + m}}.$

Из уравнения (19) следует, что углы $\varphi $ и $\psi $ связаны друг с другом, и эта связь не зависит от закона изменения $\psi (t)$. Интегрируя уравнение (19) при начальных условиях

(21)

$\psi (0) = \varphi (0) = 0,$

вытекающих из условий (10), получим

(22)

$\varphi (t) = \frac{q}{D}Arctg(D{\text{tg}}\frac{\psi }{2}) - \frac{\psi }{2},$

где введены обозначения

(23)

$q = 1 + 2{{m}_{k}}r_{k}^{0}a{{I}^{{ - 1}}},\quad D = \sqrt {1 + 4{{m}_{k}}a(r_{k}^{0} + \nu a){{I}^{{ - 1}}}} .$

Когда конец вектора ${{\rho }_{k}}$ движется по замкнутой окружности А, угол $\psi $ изменяется от 0 до 2π. На интервалах $\psi \in \left( {0,\pi } \right)$ и $\psi \in \left( {\pi ,{\text{2}}\pi } \right)$ функция ${\text{tg}}(\psi {\text{/}}2)$ изменяется, соответственно, сначала от 0 до $ \pm \infty $, а затем от $ - \infty $ до 0. При этом Arctg в (22) монотонно возрастает от 0 до π, так что при $\psi = 2\pi $ угол $\varphi $, согласно (22), получает приращение

(24)

$\Delta \varphi = \pi \left( {\frac{q}{D} - 1} \right).$

Здесь константы q и D определены равенствами (23).

Естественно предполагать, что масса тела Р значительно больше, чем масса ${{m}_{k}}$ точки ${{Q}_{k}}$, и ${{m}_{k}}{{(r_{k}^{0})}^{2}} \ll I.$ Тогда, как следует из формул (23), имеем $q < D$, и, согласно (24), $\Delta \varphi < 0.$ Таким образом, тело Р вращается вокруг оси $C{{x}_{3}}$ в направлении, противоположном вращению вектора ${{\rho }_{k}}$, которое выбрано положительным на рис. 2.

Вектор ${{\rho }_{k}}$ может совершить несколько оборотов по окружности А. При N оборотах полный угол поворота тела Р, согласно (24), составит

(25)

$\left| {\Delta \varphi } \right| = \frac{{N\pi \left( {D - q} \right)}}{D}.$

Константы D и q, входящие в правую часть равенства (25), зависят от радиуса а окружности А. Представляет интерес случай малых радиусов, в котором движение точки ${{Q}_{k}}$ происходит в ограниченной области внутри тела Р. Правая часть равенства (25) монотонно зависит от радиуса а и убывает с уменьшением а. На основе равенств (23) получим оценку:

(26)

$\left| {\Delta \varphi } \right| \sim 2N\pi \nu {{m}_{k}}{{a}^{2}}{{I}^{{ - 1}}}\quad {\text{при}}\quad a \to {\text{0}}{\text{.}}$

Следовательно, поворот тела Р на заданный угол $\Delta \varphi $, при фиксированных массах и моментах инерции, можно осуществить при малом радиусе а за счет увеличения числа оборотов N, причем справедливо соотношение

$a \sim \sqrt {\frac{{\left| {\Delta \varphi } \right|I}}{{2\pi \nu {{m}_{k}}N}}} \,.$

Для осуществления пространственной переориентации плоские повороты вокруг осей $C{{x}_{1}}$ и $C{{x}_{2}}$ осуществляются аналогично повороту вокруг оси $C{{x}_{3}}$. Для этого две другие подвижные массы должны выполнять плоские повороты в двух других плоскостях, перпендикулярных осям $C{{x}_{1}}$ и $C{{x}_{2}}$ и проходящим, как и плоскость $C{{x}_{1}}{{x}_{2}}$, через центр масс С тела Р. Заметим, что оси плоских поворотов являются главными центральными осями тела $P + {{Q}^{0}}$ и, вообще говоря, отличаются от главных центральных осей тела Р.

ОБСУЖДЕНИЕ

Предложенный алгоритм переориентации предполагает поочередное движение трех подвижных масс ${{Q}_{i}}$ по окружностям в трех плоскостях. Радиусы этих окружностей и число оборотов по ним могут быть различными. Векторы $r_{i}^{0}$ начальных положений точек ${{Q}_{i}}$ должны удовлетворять условию (5). В случае трех подвижных масс (n = 3) это условие означает, что точки $Q_{i}^{0}$ лежат в одной плоскости, проходящей через центр масс С. Данное условие представляет собой некоторое ограничение, которое может оказаться неудобным с точки зрения конструкции системы управления. Представляется целесообразным введение еще одной вспомогательной массы, которая остается неподвижной. В случае n = 4 условие (5) означает, что центр масс С лежит внутри тетраэдра с вершинами в точках $Q_{i}^{0}$. Это условие менее ограничительно и позволяет разместить точки $Q_{i}^{0}$ на значительном удалении от центра масс С тела Р. Что касается четвертой (неподвижной) массы, то она может быть использована для размещения полезного груза.

Главное допущение, сделанное в работе, состоит в отсутствии внешних сил. Оно с хорошей точностью выполняется в случае быстрых поворотов тела, когда силы его взаимодействия с внутренними массами значительно превышают внешние силы, для космических аппаратов и некоторых других подвижных объектов. Оценки влияния внешних сил в случае быстрой переориентации приведены в работе [9].

ЗАКЛЮЧЕНИЕ

Предложен новый алгоритм переориентации твердого тела при помощи нескольких (четырех) вспомогательных подвижных масс. Переориентация осуществляется посредством трех последовательных плоских поворотов тела вокруг главных центральных осей инерции виртуального твердого тела $P + {{Q}^{0}}$. Вспомогательные массы совершают плоские круговые движения в нескольких областях, расположение которых может быть достаточно свободно выбрано относительно тела. Радиусы этих движений и размеры областей могут быть взяты достаточно малыми за счет увеличения числа оборотов. Предложенный алгоритм может представлять интерес для мобильных роботов, космических аппаратов и других подвижных объектов.

Список литературы

Huda M.N., Yu H. Trajectory tracking control of an underactuated capsubot // Autonomous Robots. 2015. V. 39. № 2. P. 183–198.
Huda M.N., Yu H., Cang S. Behavior-based control approach for the trajectory tracking of an underactuated planar capsule robot // IET Control Theory and Applications. 2015. V. 9. P. 163–175.
Liu Y., Pavlovskaya E., Wiercigroch M. Experimental verification of the vibro-impact capsule model // Nonlinear Dynamics. 2016. V. 83. P. 1029–1041.
Zhan X., Xu J., Fang H. A vibration-driven planar locomotion robot – Shell // Robotica. 2018. V. 36. № 9. P. 1402–1420.
Xu J., Fang H. Improving performance: recent progress on vibration-driven locomotion systems // Nonlinear Dynamics. 2019. V. 98. № 4. P. 2651–2669.
Черноусько Ф.Л. Оптимальное управление движением двухмассовой системы // ДАН. 2018. Т. 480. № 5. С. 528–532.
Шматков А.М. Осуществление заданного движения твердого тела относительно своего центра масс перемещением материальной точки // ДАН. 2019. Т. 489. № 2. С. 147–151.
Chernousko F.L. Two- and three-dimensional motions of a body controlled by an internal movable mass // Nonlinear Dynamics. 2020. V. 99. № 1. P. 793–802.
Chernousko F.L. Reorientation of a rigid body by means of internal masses // Nonlinear Dynamics. 2020. V. 102. P. 1209–1214.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал