Доклады Российской академии наук. Физика, технические науки, 2022, T. 504, № 1, стр. 41-46

1. Проблему выбора наилучшей траектории для самолета исследуют давно. Исходно цель состояла в достижении заданной высоты при минимизации времени движения или расхода топлива, однако с ростом скорости самолетов потребовалось одновременно с этим получать необходимую скорость полета [1]. При этом оптимизацию крейсерского участка траектории проводили отдельно [2]. Для воздушных судов, движущихся с дозвуковой скоростью, можно было произвести дополнительную декомпозицию задачи и тем самым упростить решение [3]. Резкий рост цен на нефть, вызвавший удорожание авиационного топлива, повысил актуальность его экономии. В связи с этим потребовалось значительно более точно учитывать как аэродинамические ограничения, так и ограничения на тягу двигателей [4]. В дальнейшем используемые математические модели продолжали усложняться [5], для чего потребовалось применение моделей, во все большей степени основывающихся на использовании численных методов [6]. Использование более мощных бортовых компьютеров сделало возможной оптимизацию траекторий по расходу топлива в режиме реального времени, с учетом текущих воздушных потоков [7, 8]. В последние годы все больше внимания уделяют снижению различных воздействий со стороны самолета на окружающую среду [9, 10], что тесно связано с проблемой экономии топлива [11]. Также возникли задачи экономии электрической энергии, поскольку появились воздушные суда, использующие соответствующие источники [12]. Усиливается интерес к сверхзвуковой авиации как в связи с исследованиями физических процессов, наблюдающихся при движении летательных аппаратов [13], так и в связи с развитием численных методов, описывающих эти процессы [14]. Использование новых материалов позволило перейти к изучению устройств, которые могут перемещаться с гиперзвуковыми скоростями [15].

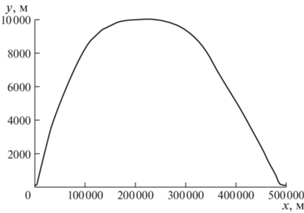
Выбор наилучшей траектории носит комплексный характер [16]. Стандартный коммерческий полет имеет траекторию [17], которая значительно отличается от типичной дозвуковой траектории, оптимальной по расходу топлива, пример которой [18] показан на рис. 1. Наиболее заметное отличие – отсутствие крейсерского этапа полета. Причина в том, что с точки зрения теории для экономии топлива оказывается целесообразным сначала набрать большую высоту полета, преобразовав внутреннюю энергию топлива в потенциальную энергию дозвукового самолета, а затем постепенно использовать этот резерв в процессе снижения до конечной точки полета. На практике приходится учитывать многочисленные ограничения, не связанные напрямую с техническими характеристиками самолета. Наиболее очевидным является то, что по современным воздушным трассам одновременно движется большое количество самолетов, и поэтому использование траекторий с постоянно изменяющейся высотой значительно усложнит управление воздушным движением и создаст риск столкновения в воздухе. Поэтому перелет между крупными центрами авиационных перевозок происходит, как правило, на постоянной высоте. Экипаж может сам (или по указанию авиадиспетчера) выбрать один из разрешенных эшелонов полета. Изменения эшелона во время полета случаются нечасто. Таким образом, возможности экономии топлива за счет глобальной оптимизации траектории дозвукового гражданского лайнера существенно ограничены, и на практике необходимо применять только локальную оптимизацию. Локальные решения, принимаемые в процессе полета, зависят во многом от бортовых автоматических систем. Используемые в них алгоритмы формируют на основе общего подхода к глобальной оптимизации [19]. Он, как правило, начинается с разбиения траектории на три этапа: взлет, крейсерский режим и посадка. Далее рассматривают три отдельные задачи [17, 20] и строят полное решение [21, 22]. Для их решения используют разнообразные численные методы [23, 24], но они, как правило, дают только субоптимальные траектории. Точные зависимости должны соответствовать принципу максимума Понтрягина, однако применение этого принципа затруднено большим количеством фазовых ограничений. Другим способом получения точных решений является метод динамического программирования Беллмана.

В данном сообщении применена математическая модель сверхзвукового пассажирского самолета, максимально приближенная к аналогичным моделям дозвуковых воздушных судов. Она учитывает самые разнообразные и весьма сложные конструктивные ограничения, которые наложены как на управляющие параметры, так и на фазовые переменные. Это обстоятельство делает применение принципа максимума крайне затруднительным, но существенно облегчает использование метода динамического программирования в классической форме, поскольку уменьшает количество вариантов возможных перемещений центра масс самолета, которые нужно перебрать. Этот метод позволил провести оптимизацию всей траектории целиком, без предварительного разделения на участки и последующей стыковки полученных фрагментов. В отличие от ограничений, накладываемых особенностями конструкции, многочисленные ограничения, наложенные действующими правилами на допустимые траектории движения гражданских самолетов, не были учтены совершенно. Однако в результате вычислений выяснилось, что оптимальные решения весьма удобны для применения в рамках указанных ограничений.

Заметим, что в работе все размерные величины представлены в системе единиц СИ.

2. Для минимизации расхода топлива важно найти оптимальное управление в вертикальной плоскости. Поэтому будем полагать, что вся траектория полета находится в этой плоскости. Пусть масса самолета в текущий момент времени равна $m$. Обозначим абсциссу и ординату центра масс самолета через $x$ и $y$ соответственно. Обозначим через $\theta $ угол, который составляет с осью абсцисс вектор скорости этого центра, причем модуль вектора равен $V$. Тогда уравнения движения самолета имеют следующий вид:

Здесь через g обозначено ускорение свободного падения, ${{n}_{x}}$ и ${{n}_{y}}$ обозначают величины тангенциальной и нормальной скоростной перегрузки соответственно, а функция ${{Q}_{t}}$ задает секундный расход топлива, зависящий от числа Маха $M$, высоты полета $y$ и тяги $P$.

Величина угла $\theta $ должна удовлетворять условию $ - 45^\circ \leqslant \theta \leqslant 45^\circ $. Заметим, что для приведенных далее примеров оптимальных траекторий $ - 11^\circ < \theta < 6^\circ $.

Поскольку сила лобового сопротивления направлена против вектора скорости, то

где через $\rho (y)$ обозначена плотность атмосферы в зависимости от высоты, а через $S$ обозначена площадь крыла самолета. Входящий в формулу (2) коэффициент лобового сопротивления ${{C}_{x}}$ зависит от коэффициента подъемной силы ${{C}_{y}}$ и числа Маха $M$.

Будем полагать, что вектор силы тяги с модулем $P$ всегда направлен вдоль вектора скорости. Тогда нормальная скоростная перегрузка определяется формулой

Должно выполняться условие $0 \leqslant {{n}_{y}} \leqslant n_{y}^{{\max }}$, где $n_{y}^{{\max }}$ = 4. Заметим, что для приведенных далее примеров оптимальных траекторий $0.8 < {{n}_{y}} < 1.3$. Величина коэффициента подъемной силы должна удовлетворять условию $0 \leqslant {{C}_{y}} \leqslant {{C}_{{y\,\max }}}(M)$.

Высота полета $y$ должна быть не меньше 100 м и не больше 14000 м. Модуль $V$ вектора скорости ограничен снизу функцией ${{V}_{{\min }}}(y)$, а сверху функцией ${{V}_{{\max }}}(y)$. Суммарная тяга двигателей $P$ ограничена сверху и снизу функциями ${{P}_{{\max }}}(y,M)$ и ${{P}_{{\min }}}(y,M)$ соответственно.

Задача состоит в выборе таких функций ${{C}_{y}}(t)$ и $P(t)$, чтобы функционал

определяющий суммарный расход топлива, имел наименьшее возможное значение. В формуле (4) через $T$ обозначено требуемое время движения из заданной начальной точки траектории в конечную при заданных начальной и конечной скоростях.

Так как согласно наложенным условиям значение выражения $V\cos \theta $ никогда не обращается в нуль, можно заменить независимую переменную в (1) и использовать дальность $x$ вместо времени. Получим

Граничные условия примут вид

где через ${{x}_{0}}$ и ${{x}_{T}}$ обозначены начальная и конечная абсциссы центра масс самолета, причем без ограничения общности можно положить ${{x}_{0}} = 0$. С учетом (5) минимизируемый функционал (4) можно записать в форме

Решение задачи поиска траектории, минимизирующей функционал (7) для системы дифференциальных уравнений (5) с начальными условиями (6) и удовлетворяющей всем указанным выше условиям, было проведено численно классическим методом динамического программирования. Далее описаны наиболее интересные свойства полученных решений.

3. Площадь крыла самолета была взята равной $S = 110.16$ м². Были выбраны следующие граничные условия (6), одинаковые для всех описанных далее случаев:

Для различных значений времени движения на рис. 2 показаны оптимальные траектории, на которых видны участки набора высоты, крейсерского режима и снижения перед посадкой. Чем меньше общее время движения, тем раньше начинается набор высоты, дольше движение в крейсерском режиме и позже происходит снижение. Для самого длительного из представленных перелетов крейсерский режим практически отсутствует. Можно заметить, что по отношению к общему времени движения чувствительность скорости набора высоты больше, чем скорости снижения.

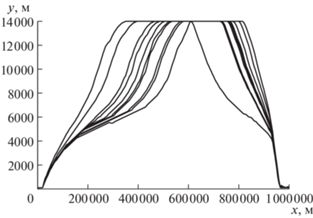
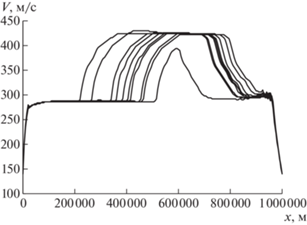
На рис. 3 показаны зависимости скорости движения самолета от дальности для тех же самых значений общего времени движения, что и на рис. 2. Видно, что типичный график состоит из семи участков. На начальном участке траектории скорость одинаково быстро растет во всех случаях. Потом в течение некоторого времени происходит движение с постоянной скоростью, практически не зависящей от общей длительности полета. Затем на некотором удалении от начальной точки траектории начинается резкий набор скорости до значения, характерного для крейсерского режима. Чем меньше общее время движения, тем раньше начинается набор скорости. Полет на крейсерском режиме характеризуется практически постоянной скоростью, одинаковой для всех рассмотренных случаев. Далее виден участок, на котором скорость резко падает почти до того же самого значения, которое было до ее роста при переходе к крейсерскому режиму. Указанное уменьшение скорости начинается тем ближе к начальной точке траектории, чем больше общее время движения. Потом виден участок, на котором скорость почти постоянна и слабо отличается от одной траектории к другой. Завершающее движение происходит при резком снижении скорости, практически одинаковом для всех случаев. Как и на рис. 2, самый длительный перелет не имеет участка, характерного для крейсерского режима.

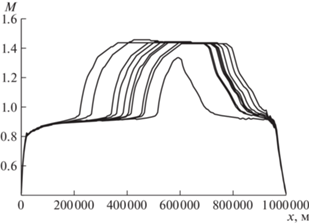
Из рис. 4 представлены зависимости значения числа Маха от дальности для того же набора траекторий, что и на рис. 2 и 3. Каждую кривую можно разбить на те же семь участков, что и на рис. 3. Видно, что участки, предшествующие выходу на крейсерский режим и следующие после него, соответствуют дозвуковым режимам полета. На том участке до крейсерского режима, где скорость движения почти одинакова для всех вариантов, число Маха медленно увеличивается. Переход к сверхзвуковому полету происходит при очень быстром росте скорости. В рамках крейсерского режима число Маха практически постоянно и равно приблизительно 1.44, а на участке примерного постоянства скорости после окончания этого режима число Маха медленно уменьшается. При этом сам выход из крейсерского режима происходит хотя и с быстрым уменьшением данного числа, однако менее резким, чем при переходе к сверхзвуковому полету.

4. Полученное решение представляется удобным для реализации. Начальные участки траекторий отличаются незначительно друг от друга, а различие между конечными участками еще меньше. Это позволяет унифицировать элементы движения самолетов на небольшом удалении от аэродромов взлета и посадки. Данное обстоятельство очень важно для упорядочения плотного потока воздушных судов в районах крупных транспортных узлов. Сверхзвуковой полет сопровождается распространением ударных волн, оказывающих существенное акустическое воздействие на живые организмы, а иногда и на элементы зданий и сооружений. Вычисления показывают, что оптимальное движение со сверхзвуковой скоростью начинается и оканчивается на высотах около шести километров, а крейсерская часть полета происходит на высоте четырнадцати километров. Акустическое воздействие при этих условиях можно полагать приемлемым. Еще одно полезное свойство полученных траекторий заключается в удобстве реализации оптимального управления, так как, например, главные отличия между скоростями движения для разных случаев сводятся к изменению моментов времени перехода от одной скорости к другой, как это видно из рис. 3.