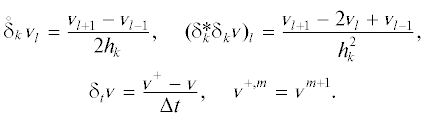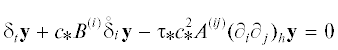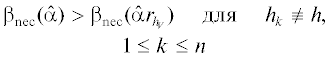Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 492, № 1, стр. 31-37

Среди методов численного решения систем уравнений газовой динамики существуют методы, основанные на предварительной регуляризации уравнений, в том числе кинетической (квазигазодинамической, КГД) регуляризации [1, 2]. В баротропном случае системы уравнений с КГД-регуляризацией были введены и исследованы в [3–5], а разнообразные их приложения даны в том числе в [6–8]. В данном сообщении изучается явная двухслойная по времени и симметричная по пространству разностная схема для такой системы уравнений, линеаризованной на постоянном решении (с произвольной скоростью). В многомерном случае впервые выводятся критерий и более простые как необходимые, так и достаточные условия L²-диссипативности решений задачи Коши для этой схемы в случае равномерной прямоугольной сетки и разного выбора параметра регуляризации τ в зависимости от сетки. Используется спектральный метод [9]. Ранее авторами подобные результаты были получены в 1D-случае [10–13].

Система уравнений баротропной газовой динамики с КГД-регуляризацией из [4] состоит из уравнений баланса массы и импульса:

в ${{\mathbb{R}}^{n}}$, $n = 1,2,3$ при $t \geqslant 0$. Искомые плотность ρ > 0 и скорость газа ${\mathbf{u}} = ({{u}_{1}},\; \ldots ,\;{{u}_{n}})$ зависят от (x, t), где $x = ({{x}_{1}},\; \ldots ,\;{{x}_{n}})$, а $p(\rho )$ – давление, с $p{\text{'}}(\rho ) > 0$. Операторы div и $\nabla = ({{\partial }_{1}},\; \ldots ,\;{{\partial }_{n}})$ берутся по x, а ${{\partial }_{t}} = \tfrac{\partial }{{\partial t}}$, ${{\partial }_{i}} = \tfrac{\partial }{{\partial {{x}_{i}}}}$. Символы $ \otimes $ и $ \cdot $ означают тензорное и скалярное произведение векторов, а дивергенция тензора берется по его первому индексу.

Регуляризованные поток массы j и тензор вязких напряжений $\Pi = {{\Pi }_{{NS}}} + {{\Pi }_{\tau }}$ таковы

где Π_NS – тензор Навье–Стокса с $\nabla {\mathbf{u}} = {\text{\{ }}{{\partial }_{i}}{{u}_{j}}{\text{\} }}_{{i,j = 1}}^{n}$, $\mathbb{I}$ – единичный тензор, ${\mathbf{m}}$, ${\mathbf{\hat {m}}}$ и Π_τ – регуляризующие импульсы и тензор, $\mu = \mu (\rho ,{\mathbf{u}}) > 0$ и λ = $\lambda (\rho ,{\mathbf{u}})$ ≥ 0 – коэффициенты вязкости, $\tau = \tau (\rho $, u) > 0 – параметр релаксации.

Напомним линеаризацию системы (1)–(3) на постоянном решении $\rho (x,t) \equiv {{\rho }_{ * }} > 0$, u(x, t) ≡ ${{{\mathbf{u}}}_{ * }}$ = = $({{u}_{{ * 1}}}, \ldots ,{{u}_{{ * n}}})$ [3]. Пусть ${{c}_{ * }} = \sqrt {p{\text{'}}({{\rho }_{ * }})} $ – фоновая скорость звука, а ${{\tau }_{ * }} = \tau ({{\rho }_{ * }},{{{\mathbf{u}}}_{ * }})$, ${{\mu }_{ * }} = \mu ({{\rho }_{ * }},{{{\mathbf{u}}}_{ * }})$, ${{\lambda }_{ * }} = \lambda ({{\rho }_{ * }},{{{\mathbf{u}}}_{ * }})$, и последние задаются формулами ${{\mu }_{ * }} = {{\alpha }_{s}}{{\tau }_{ * }}{{\rho }_{ * }}c_{ * }^{2}$, ${{\lambda }_{ * }} = {{\alpha }_{{1s}}}{{\tau }_{ * }}{{\rho }_{ * }}c_{ * }^{2}$ с ${{\alpha }_{s}} \geqslant 0$, ${{\alpha }_{{1s}}} \geqslant 0$ (случай ${{\alpha }_{s}} = {{\alpha }_{{1s}}} = 0$ возможен). Положим a₁ = $\tfrac{1}{3}{{\alpha }_{s}}$ + + α_1s + 1. Подстановка в уравнения (1)–(3) решения в виде $\rho = {{\rho }_{ * }} + {{\rho }_{ * }}\tilde {\rho }$, ${\mathbf{u}} = {{{\mathbf{u}}}_{ * }} + {{c}_{ * }}{\mathbf{\tilde {u}}}$, где $\tilde {\rho }$, ${\mathbf{\tilde {u}}}$ – безразмерные малые возмущения, и отбрасывание членов 2-го порядка малости по отношению к ним приводит к линеаризованной КГД-системе уравнений для ${\mathbf{z}} = {{(\tilde {\rho }\,{\mathbf{\tilde {u}}})}^{{\text{т}}}}$:

в ${{\mathbb{R}}^{n}}$ при $t \geqslant 0$, где ${{B}^{{(i)}}}$ и ${{A}^{{(ij)}}}$ – матрицы порядка n + 1. Здесь и ниже по повторяющимся индексам i, j (и только по ним) предполагается суммирование от 1 до n. Пусть векторы-столбцы ${{{\mathbf{e}}}_{0}},\; \ldots ,\;{{{\mathbf{e}}}_{n}}$ образуют стандартный координатный базис в ${{\mathbb{R}}^{{n + 1}}}$, тогда при всех k, l, $k \ne l$. Здесь и ниже ${{M}_{k}} = \tfrac{{{{u}_{{ * k}}}}}{{{{c}_{ * }}}}$, I_k – единичная матрица порядка k, а $diag{\text{\{ }}{{p}_{1}},\; \ldots ,\;{{p}_{k}}{\text{\} }}$ – диагональная матрица с указанными диагональными элементами. Ясно, что B⁽ⁱ⁾ и ${{A}^{{(ij)}}}$ – симметричные матрицы, и ${{A}^{{(kl)}}} = {{A}^{{(lk)}}}$. Отметим, что

Для решения системы типа (4) с начальным условием ${{\left. {\mathbf{z}} \right|}_{{t = 0}}} = {{{\mathbf{z}}}_{0}}$ верна оценка [3]

Введем сетку ${{\omega }_{{kh}}}$ по x_k с узлами lh_k, $l \in \mathbb{Z}$ и шагом ${{h}_{k}} > 0$, $1 \leqslant k \leqslant n$. Пусть ${{\bar {\omega }}^{{\Delta t}}}$ – сетка по t с узлами ${{t}_{m}} = m\Delta t$, $m \geqslant 0$ и шагом $\Delta t > 0$. Определим разностные операторы

Введем прямоугольную сетку ${{\omega }_{{\mathbf{h}}}}: = {{\omega }_{{1h}}} \times \; \ldots \; \times {{\omega }_{{nh}}}$ в ${{\mathbb{R}}^{n}}$ с ${\mathbf{h}} = ({{h}_{1}},\; \ldots ,\;{{h}_{n}})$ и положим ${{h}_{{min}}}: = \mathop {min}\limits_{1 \leqslant k \leqslant n} {{h}_{k}}$, h_V = = ${{({{h}_{1}}\; \ldots \;{{h}_{n}})}^{{1/n}}}$, ${{h}_{{max}}}: = \mathop {max}\limits_{1 \leqslant k \leqslant n} {{h}_{k}}$.

Аппроксимируем систему уравнений (4) с помощью введенных разностных операторов и получим явную по t разностную схему, трехточечную по каждому направлению ${{x}_{1}}, \ldots ,{{x}_{n}}$

на ${{\omega }_{{\mathbf{h}}}} \times {{\omega }^{{\Delta t}}}$, где ${{({{\partial }_{k}}{{\partial }_{k}})}_{h}}: = \delta _{k}^{ * }{{\delta }_{k}}$ и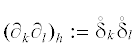 при k ≠ l. Такая разностная схема возникает и при линеаризации схем для исходных уравнений (1)–(3), см. в том числе [14].

Пусть H – гильбертово пространство вектор-функций ${\mathbf{v}}$: ${{\omega }_{{\mathbf{h}}}} \to {{\mathbb{C}}^{{n + 1}}}$, суммируемых в квадрате на ω_h, со скалярным произведением

Поставим вопрос об условиях справедливости сеточного аналога оценки (6) – оценки

Она эквивалентна свойствам ${{\left\| \mathcal{A} \right\|}_{{H \to H}}} \leqslant 1$ оператора 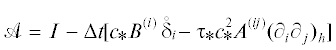и H-диссипативности схемы ${\text{||}}{{{\mathbf{y}}}^{m}}{\text{|}}{{{\text{|}}}_{H}} \leqslant {\text{||}}{{{\mathbf{y}}}^{{m - 1}}}{\text{|}}{{{\text{|}}}_{H}} \leqslant \; \ldots \; \leqslant {\text{||}}{{{\mathbf{y}}}^{0}}{\text{|}}{{{\text{|}}}_{H}}$ для всех ${{{\mathbf{y}}}^{0}} \in H$, $m \geqslant 1$.

Пусть Δt и ${{\tau }_{ * }}$ задаются формулами

с параметрами β > 0 (числом Куранта) и α > 0, где ${{h}_{\tau }} = {{h}_{\tau }}({\mathbf{h}}) > 0$ (в том числе ${{h}_{\tau }} = {{h}_{{min}}}$, ${{h}_{V}}$ или h_max), а величины $\tilde {\beta }$, $\hat {\alpha }$, ${{\alpha }_{{{{h}_{\tau }}}}}$, ${{\hat {\alpha }}_{{{{h}_{\tau }}}}}$ введены для удобства (при этом ${{\alpha }_{{{{h}_{\tau }}}}} = \alpha $, ${{\hat {\alpha }}_{{{{h}_{\tau }}}}} = \hat {\alpha }$ для ${{h}_{\tau }} = {{h}_{{min}}}$). Кроме того, M = = $\tfrac{{\left| {{{{\mathbf{u}}}_{ * }}} \right|}}{{{{c}_{ * }}}}$ – фоновое число Маха. Ниже выводятся условия на $\tilde {\beta }$ в зависимости от ${{\alpha }_{{{{h}_{\tau }}}}}$ или β – от ${{\hat {\alpha }}_{{{{h}_{\tau }}}}}$, связанные с выполнением оценки (8).

Следуя [9], рассмотрим частные решения схемы (7) вида ${\mathbf{y}}_{{\mathbf{k}}}^{m}(\xi ) = {{e}^{{{\text{i}}{\mathbf{k}}\xi }}}{{{\mathbf{w}}}^{m}}(\xi )$, где ${\mathbf{k}} \in {{\mathbb{Z}}^{n}}$, $m \geqslant 0$, i – мнимая единица и $\xi = {{({{\xi }_{1}}, \ldots ,{{\xi }_{n}})}^{T}} \in {{[0,2\pi ]}^{n}}$ – параметр. Их подстановка в (7) с учетом формул (9) дает явную рекуррентную формулу ${{{\mathbf{w}}}^{ + }} = {{G}_{{\mathbf{s}}}}{\mathbf{w}}$ на ${{\bar {\omega }}^{{\Delta t}}}$, с матрицами

где G_s – символ оператора $\mathcal{A}$, ${\mathbf{s}} = ({{s}_{1}},\; \ldots ,\;{{s}_{n}})$ и а l_k = 0 при $0 \leqslant {{\xi }_{k}} \leqslant \pi $ либо l_k = 1 при $\pi < {{\xi }_{k}} \leqslant 2\pi $. Кроме того, ${{\delta }^{{(ij)}}}$ – символ Кронекера.

Введем вектор ${\mathbf{M}} = {{({{M}_{1}}, \ldots ,{{M}_{n}})}^{T}}$, тогда M = |M| – число Маха, а также вектор-строку ${\mathbf{\zeta }} = ({{d}_{1}}{{s}_{1}}$, ..., d_ns_n) и положим $d = {{(d_{1}^{2} + \; \ldots \; + d_{n}^{2})}^{{1/2}}}$.

Лемма 1. 1. Матрицы ${{B}_{{\mathbf{s}}}}$ и ${{A}_{{\mathbf{s}}}}$ можно записать в блочном виде

c ${{a}_{{\mathbf{M}}}}: = {{(\zeta {\mathbf{M}})}^{2}} + {{{\mathbf{M}}}^{T}}Q{\mathbf{M}}$ и матрицей Q = $diag{\text{\{ }}{{q}_{1}}$, ... ..., q_n} с ${{q}_{k}} = d_{k}^{2}{{\sigma }_{k}}$, $1 \leqslant k \leqslant n$.

2. Справедливо матричное неравенство $B_{{\mathbf{s}}}^{2} \leqslant {{A}_{{\mathbf{s}}}}$.

Доказательство. 1. В силу формул для матриц B⁽ⁱ⁾ и A^(ij) можно записать

Указанный вид матриц B_s и A_s следует из этих формул, а также ${{\left| {\mathbf{\zeta }} \right|}^{2}} + {{\delta }^{{(ii)}}}{{q}_{i}} = {{d}^{2}}$ и

2. Непосредственно проверяется формула

где $trQ = {{\delta }^{{(ii)}}}{{q}_{i}}$ – след матрицы Q. Из нее следуют матричные неравенства

Правое неравенство очевидно (так как ${{a}_{1}} \geqslant 1$ и $Q \geqslant 0$), а левое эквивалентно неравенству

В силу свойств $Q \geqslant 0$ и диагональности Q последнее следует из неравенств

Обозначим через ${{\lambda }_{{max}}}(A)$ максимальное собственное значение эрмитовой матрицы A.

Теорема 1. Свойство ${{\left\| \mathcal{A} \right\|}_{{H \to H}}} \leqslant 1$ эквивалентно спектральному свойству

Теорема обобщается на любой линейный сеточный оператор с конечным шаблоном $\mathcal{A}$: H → H.

Пусть $[A,B] = AB - BA$ – коммутатор матриц A и B (порядка k). Для эрмитовых матриц A и B матрица ${\text{i}}[A,B]$ также эрмитова и справедливы простые оценки

В самом деле, для любого ${\mathbf{w}} \in {{\mathbb{C}}^{k}}$ имеем

Дадим необходимые условия и достаточные условия справедливости оценки (8).

Теорема 2. Выполнение матричных неравенств:

с каким-либо ε > 0 соответственно необходимо и достаточно, необходимо, достаточно для справедливости оценки (8). Как следствие, при $\mathop {max}\limits_{{\mathbf{s}} \in S} {{\lambda }_{{max}}}({{A}_{{\mathbf{s}}}}) \leqslant \bar {\lambda }$ для справедливости оценки (8) достаточно выполнение неравенства

Доказательство. Подобно [11], условие (10) эквивалентно матричному неравенству $G_{{\mathbf{s}}}^{ * }{{G}_{{\mathbf{s}}}} \leqslant {{I}_{{n + 1}}}$, т.е. $\tilde {\beta }F_{{\mathbf{s}}}^{ * }{{F}_{{\mathbf{s}}}} \leqslant 2({{F}_{{\mathbf{s}}}} + F_{{\mathbf{s}}}^{ * })$, для всех ${\mathbf{s}} \in S$. Подставив сюда выражение для F_s и сократив обе части на $8{{\alpha }_{{{{h}_{\tau }}}}}$, получим неравенство (12).

Фиксируем $1 \leqslant k \leqslant n$, возьмем ${{\sigma }_{l}} = 0$ при k ≠ l и после сокращения на $d_{k}^{2}$ (при ${{\sigma }_{k}} \ne 0$) получим относящееся только к направлению ${{x}_{k}}$ неравенство

при всех ${{\sigma }_{k}} \in (0,\;1]$. Из него при ${{\sigma }_{k}} = 1$ и ${{\sigma }_{k}} \to + 0$ вытекают неравенства (13).

В силу оценки (11) неравенство (12) следует из (14), а так как $B_{{\mathbf{s}}}^{2} \leqslant {{A}_{{\mathbf{s}}}}$, то и из неравенства

Оно эквивалентно неравенству для собственных значений ${{\lambda }_{k}}({{A}_{{\mathbf{s}}}})$ матрицы A_s:

Поскольку ${{\lambda }_{k}}({{A}_{{\mathbf{s}}}}) \geqslant 0$, то последнее неравенство следует из

При $\mathop {max}\limits_{{\mathbf{s}} \in S} {{\lambda }_{{max}}}({{A}_{{\mathbf{s}}}}) \leqslant \bar {\lambda }$, выбрав $\varepsilon = \tfrac{1}{{2{{\alpha }_{{{{h}_{\tau }}}}}}}\mathop {\bar {\lambda }}\nolimits^{ - 1/2} $, выведем достаточное условие (15).

Отметим, что при выводе условий (13) вид матриц A^(ij) с i ≠ j роли не играл.

Нетрудно найти собственные значения матрицы A^(kk) и в том числе

В частности, ${{\lambda }_{{kmax}}} = {{a}_{1}} + {{\alpha }_{s}}$ при M_k = 0. Поскольку ${{a}_{1}} \geqslant 1$, то

Теорема 3. Выполнение условия

необходимо для справедливости оценки (8). Здесь ${{r}_{{{{h}_{\tau }}}}} = \frac{{{{h}_{\tau }}}}{{{{h}_{{min}}}}}$.

Если ${{h}_{1}} = \; \ldots \; = {{h}_{n}} = {{h}_{\tau }} = h$, то ${{\beta }_{{{\text{nec}}}}}(\hat {\alpha })$ не зависит от $h$ и принимает вид

Доказательство. Первое из неравенств (13) эквивалентно числовому неравенству

так как ${{A}^{{(kk)}}} \geqslant 0$. Поскольку ${{({{B}^{{(k)}}})}^{2}} \leqslant {{A}^{{(kk)}}}$ согласно (5), то второе из неравенств (13) выполнено при $\tilde {\beta } \leqslant 2{{\alpha }_{{{{h}_{\tau }}}}}$. С другой стороны, $({{B}^{{(k)}}})_{{11}}^{2} = A_{{11}}^{{(kk)}} > 0$, поэтому второе из неравенств (13) влечет неравенство $\tilde {\beta } \leqslant 2{{\alpha }_{{{{h}_{\tau }}}}}$ и в итоге ему эквивалентно (подобно [11]). Отсюда после перехода от $\tilde {\beta }$ и ${{\alpha }_{{{{h}_{\tau }}}}}$ к β и $\mathop {\hat {\alpha }}\nolimits_{{{h}_{\tau }}} $ следует условие (16).

Максимум ${{\beta }_{{{\text{nec}}}}}(\hat {\alpha }{{r}_{{{{h}_{\tau }}}}})$ по $\hat {\alpha } > 0$ достигается в одной точке $\hat {\alpha } = {{\hat {\alpha }}_{*}}({{h}_{\tau }})$ и

отметим, что ${{\beta }_{{{\text{nec}}}}}({{\hat {\alpha }}_{*}}({{h}_{\tau }}){{r}_{{{{h}_{\tau }}}}})$ не зависит от выбора h_τ. При ${{h}_{1}} = \; \ldots \; = {{h}_{n}} = {{h}_{\tau }} = h$ имеем ${{\hat {\alpha }}_{*}}({{h}_{\tau }}) = {{\hat {\alpha }}_{{*1}}}$, а неравенство в (18) переходит в равенство, т.е. переход от квадратной сетки к любой прямоугольной отнюдь не приводит к уменьшению значения ${{\beta }_{{{\text{nec}}}}}({{\hat {\alpha }}_{*}}({{h}_{\tau }}){{r}_{{{{h}_{\tau }}}}})$.

Однако значение ${{\hat {\alpha }}_{*}}({{h}_{\tau }})$, играющее важную роль на практике, существенно зависит от выбора ${{h}_{\tau }}$. Отметим, что, во-первых, ${{\hat {\alpha }}_{*}}({{h}_{{min}}}) \geqslant {{\hat {\alpha }}_{{*1}}}$ при любых h. Во-вторых, в случае, когда $\left| {{{M}_{k}}} \right|$ не зависит от k, величина ${{\lambda }_{{kmax}}}$ тоже не зависит от k и тогда имеем

где ${{h}_{k}} = {{h}_{{min}}} \leqslant {{h}_{l}} \leqslant {{h}_{m}} = {{h}_{{max}}}$ и (k, l, m) – перестановка индексов (1, 2, 3), и при ${{h}_{l}} = {{h}_{m}}$ величина (20) наименьшая для n = 3. Здесь ${{\hat {\alpha }}_{*}}({{h}_{{min}}})$ не зависит от h, а ${{\hat {\alpha }}_{*}}({{h}_{{\,V}}})$ – зависит, и ${{\hat {\alpha }}_{*}}({{h}_{V}}) \ll {{\hat {\alpha }}_{*}}({{h}_{{min}}})$ для сетки с $\tfrac{{{{h}_{{min}}}}}{{{{h}_{{max}}}}} \ll 1$. Эти свойства ${{\hat {\alpha }}_{*}}({{h}_{{\,V}}})$ неудобны на практике.

При ${{h}_{\tau }} = {{h}_{{min}}}$ и ${{h}_{\tau }} = {{h}_{{\,V}}}$ верны также оценки снизу соответственно

Существенно, что для ${{h}_{\tau }} = {{h}_{{min}}}$ оценка равномерна по h и ее правая часть та же, что в (17), а для ${{h}_{\tau }} = h{{\,}_{V}}$ – нет; обе оценки переходят в равенства, когда $\left| {{{M}_{k}}} \right|$ не зависит от k.

Поскольку величина $\tfrac{{{{h}_{\tau }}}}{{{{h}_{{min}}}}}$ при ${{h}_{\tau }} = {{h}_{{min}}}$ не больше, чем при ${{h}_{\tau }} = {{h}_{V}}$, а вторая из величин в определении ${{\beta }_{{{\text{nec}}}}}(\hat {\alpha }{{r}_{{{{h}_{\tau }}}}})$ (с $\mathop {min}\limits_{1 \leqslant k \leqslant n} $) – не меньше, то

при условии

Если $\left| {{{M}_{k}}} \right|$ не зависит от k, то это приводит к соотношениям

и при $\tfrac{{{{h}_{{min}}}}}{{{{h}_{{max}}}}} \ll 1$, см. (20), свойство (22) выполнено для всех $\hat {\alpha }$, кроме достаточно малых.

Вторая оценка (21) сохраняет силу для любого выбора ${{h}_{\tau }}$ в качестве h_V, а соотношения (19), (23), (24) – для любого выбора ${{h}_{\tau }} > {{h}_{{min}}}$ в качестве h_V, поэтому в них выбор ${{h}_{\tau }} = {{h}_{{min}}}$ является наилучшим. Для ${{h}_{\tau }} = {{h}_{{max}}}$ ситуация только ухудшается по сравнению с ${{h}_{\tau }} = {{h}_{V}}$.

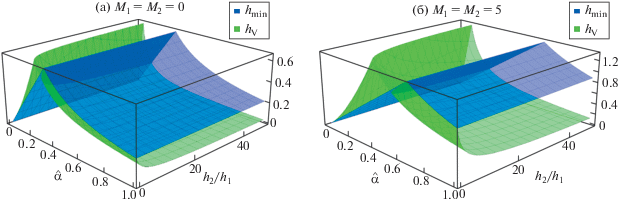
На рис. 1 при n = 2 даны графики ${{\beta }_{{{\text{nec}}}}}(\hat {\alpha }{{r}_{{{{h}_{\tau }}}}})$ для ${{h}_{\tau }} = {{h}_{{min}}}$, h_V в зависимости от $\hat {\alpha }$ и $\tfrac{{{{h}_{2}}}}{{{{h}_{1}}}}$ для ${{M}_{1}} = {{M}_{2}}$ = 0 (т.е. для числа Маха $M = 0$) и ${{M}_{1}} = {{M}_{2}} = 5$ (поэтому для M = 5) в случае ${{\alpha }_{s}} = 1$, ${{\alpha }_{{1s}}} = 0$. Они наглядно иллюстрируют выполненный выше анализ.

Перейдем к достаточному условию (15). Оно выглядит аналогично полученному в [13] другим методом для неравномерной сетки по $x$ в 1D-случае. Его можно переписать в виде

Максимум правой части достигается при $\mathop {\hat {\alpha }}\nolimits_{{{h}_{\tau }}} $ = = ${{\hat {\alpha }}_{{{{h}_{\tau }}*}}}: = \tfrac{{M + 1}}{2}\mathop {\bar {\lambda }}\nolimits^{ - 1/2} $ и равен $\tfrac{{{{{\hat {\alpha }}}_{{{{h}_{\tau }}*}}}}}{2}$, ср. с (18). Характерно, что ${{\beta }_{{{\text{nec}}}}}(\mathop {\hat {\alpha }}\nolimits_{{{h}_{\tau }}} ) \to 0$ и ${{\beta }_{{{\text{suf}}}}}(\mathop {\hat {\alpha }}\nolimits_{{{h}_{\tau }}} ) \to 0$ при $\mathop {\hat {\alpha }}\nolimits_{{{h}_{\tau }}} \to + 0$ и $\mathop {\hat {\alpha }}\nolimits_{{{h}_{\tau }}} \to + \infty $.

Для применения условия (25) оценим сверху ${{\lambda }_{{max}}}({{A}_{{\mathbf{s}}}})$. Положим ${\mathbf{r}} = ({{r}_{1}},\; \ldots ,\;{{r}_{n}})$.

Теорема 4. При n = 2, 3 верны оценки

с c₂ = 1, ${{c}_{3}} = \tfrac{9}{8}$, и при ${{h}_{1}} = \; \ldots \; = {{h}_{n}}$ последнее неравенство переходит в равенство.

Доказательство. Запишем разложение A_s = = ${{A}_{{{\mathbf{s}}0}}} + {{a}_{{\mathbf{M}}}}{{I}_{{n + 1}}} + 2{{A}_{{{\mathbf{M}}1}}}$, где

где ${\mathbf{p}} = ({{p}_{1}}, \ldots ,{{p}_{n}})$ с ${{p}_{k}} = d_{k}^{2}{{M}_{k}}$ + (1 – ${{\delta }^{{(kj)}}}){{d}_{k}}{{s}_{k}}{{d}_{j}}{{s}_{j}}{{M}_{j}}$, $1 \leqslant k \leqslant n$, а O_n – нулевая матрица порядка $n$.

Поскольку ${{\sigma }_{i}} + s_{i}^{2} = 1$, $0 \leqslant {{\sigma }_{i}} \leqslant 1$ и $\mathop {max}\limits_{1 \leqslant i \leqslant n} {{r}_{i}} = 1$, то имеем

для всех ${\mathbf{v}} = {{({{{v}}_{1}}, \ldots ,{{{v}}_{n}})}^{T}} \in {{\mathbb{R}}^{n}}$. Отсюда по формуле Рэлея ${{\lambda }_{{max}}}({{{\mathbf{\zeta }}}^{T}}{\mathbf{\zeta }} + Q) \leqslant {{c}_{n}}$ и

Отметим, что ${{\lambda }_{{max}}}({{A}_{{{\mathbf{s}}0}}}) = max\{ {{\left| {\mathbf{r}} \right|}^{2}},{{\alpha }_{s}}{{\left| {\mathbf{r}} \right|}^{2}} + {{a}_{1}}\} $ при ${{\sigma }_{1}} = \; \ldots \; = {{\sigma }_{n}} = 1$.

Далее, как и в (27), имеем

Также можно записать

Поскольку ${{\lambda }_{{max}}}({{A}_{{\mathbf{s}}}}) \leqslant {{\lambda }_{{max}}}({{A}_{{{\mathbf{s}}0}}}) + {{a}_{{\mathbf{M}}}}$ + 2λ_max(A_M1), то оценка (26) получена.

При n = 3 возможна альтернативная (27) оценка. Поскольку ${{{\mathbf{v}}}^{{\text{т}}}}{{{\mathbf{\zeta }}}^{{\text{т}}}}{\mathbf{\zeta v}} \leqslant {{\left| {\mathbf{\zeta }} \right|}^{2}}{{\left| {\mathbf{v}} \right|}^{2}}$, то

так как $d_{k}^{2}s_{k}^{2} = {{\sigma }_{k}}(1 - {{\sigma }_{k}})r_{k}^{2} \leqslant \tfrac{1}{4}r_{k}^{2}$. Поэтому в $\bar {\lambda }$ можно заменить ${{c}_{3}}$ на $min\left\{ {{{c}_{3}},\frac{3}{4} + \frac{1}{4}{{{\left| {\mathbf{r}} \right|}}^{2}}} \right\}$.

Важно, что ${{\beta }_{{{\text{nec}}}}}({{\hat {\alpha }}_{{{{h}_{\tau }}}}})$ и ${{\beta }_{{{\text{suf}}}}}({{\hat {\alpha }}_{{{{h}_{\tau }}}}})$ равномерно по M отделены от 0 и ограничены сверху.