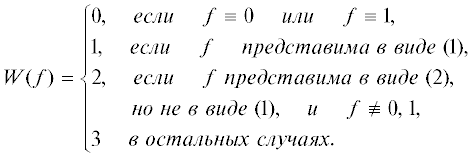Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 495, № 1, стр. 65-68

1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ВСПОМОГАТЕЛЬНЫЕ УТВЕРЖДЕНИЯ

Множество контактов контактной схемы (КС) называется ее сечением, если оно имеет хотя бы один общий контакт с каждой несамопересекающейся цепью (НЦ), соединяющей полюсы схемы. Сечение считается тупиковым, если после выбрасывания из него любого одного контакта оно перестает быть сечением [14, с. 133]. Непустое множество контактов называется пучком, если все контакты из этого множества имеют одну и ту же пару концов и концы каждого контакта различны.

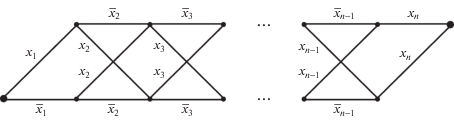
В работе [5] вводится понятие ширины КС, определяемое как наибольшее число контактов в тупиковом сечении этой схемы. Несложно показать, что: а) ширина любой КС S₁, представляющей собой параллельное соединение m несамопересекающихся цепей, где $m \in \mathbb{N}$, равна m; б) ширина любой КС S₂, представляющей собой последовательное соединение p пучков, где $p \in \mathbb{N}$, равна максимальному количеству контактов в одном пучке. Однако у введенного понятия ширины КС, с точки зрения автора, есть существенный недостаток, который мы продемонстрируем на конкретном примере. Рассмотрим известную КС $S_{ \oplus }^{n}$, где $n \geqslant 2$, реализующую линейную булеву функцию ${{x}_{1}} \oplus \; \ldots \; \oplus {{x}_{n}}$ и содержащую $4n - 4$ контактов (см. рис. 1). С интуитивной точки зрения ширина этой схемы не должна зависеть от n (если длину схемы связывать с максимальной или минимальной длиной НЦ между ее полюсами, а ширину считать вторым измерением этой схемы), однако, как легко убедиться, одним из тупиковых сечений схемы $S_{ \oplus }^{n}$ является множество, состоящее из всех ее замыкающих контактов, т.е. всех ее контактов ${{x}_{1}},{{x}_{2}}$, ..., x_n. В этом сечении содержится $2n - 2$ контактов, следовательно, ширина схемы $S_{ \oplus }^{n}$ не меньше $2n - 2$, т.е. растет с ростом n. Таким образом, приведенное определение ширины КС, по мнению автора, не всегда согласуется с интуитивным смыслом данного понятия.

В связи с вышеуказанным введем другое понятие ширины КС, которое во избежание путаницы будем называть ее равномерной шириной. Пусть S – КС и K – произвольный содержащийся в ней контакт. Обозначим через ${{W}_{K}}(S)$ наименьшее число контактов в тупиковом сечении схемы S, содержащем контакт K, и положим W(S) = $max{{W}_{K}}(S)$, где максимум берется по всем контактам K схемы S, для которых определено значение ${{W}_{K}}(S)$. Величину $W(S)$ назовем равномерной шириной схемы S. Величина ${{W}_{K}}(S)$ играет роль “локальной” ширины этой схемы в окрестности контакта K.

Предложение 1. Значение ${{W}_{K}}(S)$ определено тогда и только тогда, когда в схеме S есть хотя бы одна НЦ между полюсами, содержащая контакт K.

Предложение 2. Значение $W(S)$ определено тогда и только тогда, когда полюсы схемы $S$ не совпадают и в ней есть хотя бы одна НЦ между полюсами.

Доопределим величину $W(S)$ для случаев, когда полюсы схемы S совпадают или в ней нет ни одной НЦ между полюсами, положив в каждом из этих двух случаев $W(S) = 0$.

Для любой КС S, в которой через каждый контакт проходит хотя бы одна НЦ между полюсами этой схемы (т.е. для которой значение ${{W}_{K}}(S)$ определено для любого ее контакта K), величина W(S) играет роль наибольшей “локальной” ширины схемы S.

Нетрудно показать, что сформулированные выше утверждения а) и б) справедливы и при добавлении перед словом “ширина” слова “равномерная”. Таким образом, для указанных в формулировке этих утверждений схем S₁ и S₂ понятия ширины и равномерной ширины совпадают. Оценим сверху равномерную ширину схемы $S_{ \oplus }^{n}$, изображенной на рис. 1.

Предложение 3. Справедливо неравенство

$W(S_{ \oplus }^{n}) \leqslant 4$.

Выше было показано, что ширина схемы $S_{ \oplus }^{n}$ растет с ростом n. Таким образом, введенное определение равномерной ширины КС при рассмотрении схемы $S_{ \oplus }^{n}$, с точки зрения автора, согласуется с интуитивным смыслом понятия ширины этой схемы, в отличие от определения ширины КС, данного в [5].

Пусть $n \in \mathbb{N} \cup {\text{\{ }}0{\text{\} }}$ и $f({{\tilde {x}}^{n}})$ – булева функция, где ${{\tilde {x}}^{n}} = ({{x}_{1}}, \ldots ,{{x}_{n}})$. Введем следующие обозначения: $W(f) = min\,W(S)$, где минимум берется по всем КС S, реализующим функцию f; W(n) = $max\,W(f)$, где максимум берется по всем булевым функциям f от n переменных. По аналогии с другими подобными величинами (см., например, [14, с. 32]), назовем величину W(n) функцией Шеннона равномерной ширины контактных схем; она определяет минимально возможную равномерную ширину таких схем, достаточную для реализации произвольной булевой функции от n переменных.

Имеет место следующая тривиальная верхняя оценка величины W(n).

Предложение 4. Для любого $n \in \mathbb{N} \cup {\text{\{ }}0{\text{\} }}$ справедливо неравенство $W(n) \leqslant n$.

Элементарной конъюнкцией (переменных из множества ${\text{\{ }}{{x}_{1}},\; \ldots ,\;{{x}_{n}}{\text{\} }}$) называется выражение вида $x_{{{{i}_{1}}}}^{{{{\sigma }_{1}}}}\& \; \ldots \;\& x_{{{{i}_{r}}}}^{{{{\sigma }_{r}}}}$, где $r \in {\text{\{ }}1,\; \ldots ,\;n{\text{\} }}$, ${{i}_{1}},\; \ldots ,\;{{i}_{r}}$ – попарно различные индексы от 1 до n и ${{\sigma }_{1}},\; \ldots ,\;{{\sigma }_{r}} \in {\text{\{ }}0,\;1{\text{\} }}$; при этом полагаем

2. ОСНОВНЫЕ РЕЗУЛЬТАТЫ

Выделим два возможных представления булевой функции $f({{\tilde {x}}^{n}})$:

где $\mathcal{K}$ – элементарная конъюнкция; где $k \in \mathbb{N}$ и для любого $i \in {\text{\{ }}1,\; \ldots ,\;k{\text{\} }}$ функция ${{\varphi }_{i}}({{\tilde {x}}^{n}})$ имеет вид либо ${{\mathcal{K}}_{i}}$, либо ${{\mathcal{K}}_{i}} \vee \mathcal{K}_{i}^{'}$, где ${{\mathcal{K}}_{i}}$, $\mathcal{K}_{i}^{'}$ – элементарные конъюнкции.

Теорема 1. Для любой булевой функции $f({{\tilde {x}}^{n}})$ справедливо равенство

Все верхние оценки величины $W(f)$ в теореме 1 доказаны конструктивно, т.е. с предъявлением конкретных контактных схем, дающих эти оценки. При доказательстве нижних оценок той же величины используется следующая

Лемма 1. Пусть S – такая КС без изолированных вершин, что $W(S) \in {\text{\{ }}1,\;2{\text{\} }}$ и для каждого контакта K данной схемы определено значение ${{W}_{K}}(S)$. Тогда схема S представима в виде последовательного соединения $m$ контактных схем, где $m \in \mathbb{N}$ и каждая из этих $m$ схем представляет собой либо одиночный контакт, либо параллельное соединение двух НЦ.

Теорема 2. Для любого $n \in \mathbb{N} \cup {\text{\{ }}0{\text{\} }}$ справедливо равенство $W(n) = min(3,n)$, причем доля тех булевых функций f от n переменных, для которых $W(f) = 3$, стремится к 1 при $n \to \infty $.

Теорема 2 несложным образом вытекает из теоремы 1 и следующей леммы.

Лемма 2. Для любой булевой функции $f({{\tilde {x}}^{n}})$, $n \geqslant 2$, представимой в виде (2) и отличной от константы 1, существуют такие различные индексы $i,j \in {\text{\{ }}1,\; \ldots ,\;n{\text{\} }}$ и такие $\alpha ,\beta \in {\text{\{ }}0,\;1{\text{\} }}$, что данная функция при подстановке вместо переменных x_i и x_j значений соответственно α и β становится равна тождественному нулю.