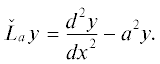Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 496, № 1, стр. 26-29

АСИМПТОТИКИ СОБСТВЕННЫХ ЗНАЧЕНИЙ В ЗАДАЧЕ ОРРА–ЗОММЕРФЕЛЬДА ДЛЯ МАЛЫХ СКОРОСТЕЙ НЕВОЗМУЩЕННОГО ТЕЧЕНИЯ

Д. В. Георгиевский^{1, 2, 3, 4, *}

¹ Московский государственный университет имени М.В. Ломоносова
Москва, Россия

² Институт проблем механики им. А.Ю. Ишлинского Российской академии наук
Москва, Россия

³ Московский центр фундаментальной и прикладной математики
Москва, Россия

⁴ Научный центр мирового уровня “Сверхзвук – МГУ”
Москва, Россия

^* E-mail: georgiev@mech.math.msu.su

Поступила в редакцию 26.08.2020
После доработки 27.11.2020
Принята к публикации 27.11.2020

DOI: 10.31857/S2686954321010045

Полный текст (PDF)

Аннотация

Проводится асимптотический анализ собственных значений и собственных функций в задаче Орра–Зоммерфельда в случае малой по определенной мере скорости основного плоскопараллельного сдвигового течения в слое ньютоновской вязкой жидкости. В качестве нулевого приближения выбираются собственные значения и соответствующие им собственные функции для состояния покоя в слое. Находятся явные аналитические выражения для их возмущений в линейном приближении. Показывается, что возмущения при малых скоростях основного сдвига собственных значений, отвечающих монотонному затуханию вблизи состояния покоя в вязком слое, таковы, что вне зависимости от профиля скорости декремент затухания остается тем же, но появляется колебательная составляющая, по порядку малости на единицу меньшая этого декремента.

Ключевые слова: задача Орра–Зоммерфельда, собственное значение, собственная функция, течение, вязкая жидкость, устойчивость, возмущение

Численно-аналитические продвижения в исследовании классических задач механики и математической физики, к которым принадлежат известная более ста лет задача Орра–Зоммерфельда и ее обобщения, представляют теоретический и определенный практический интерес [1–6]. В большинстве исследований, связанных с нахождением собственных чисел и собственных функций в задаче Орра–Зоммерфельда (см. обзоры в [7, 8]), анализ велся для конкретных видов профилей невозмущенного течения. В основном такими профилями служили отрезок (куэттовские течения), парабола (пуазейлевские течения) либо их комбинация, а также, возможно, какие-то другие отдельно выбранные кривые. Ниже проводится асимптотический анализ собственных чисел и собственных функций в этой задаче вблизи состояния покоя при произвольной малой скорости невозмущенного плоскопараллельного течения в вязком слое.

1. Обратимся к классической в линеаризованной теории устойчивости задаче Орра–Зоммерфельда

(1)

${{\varphi }^{{IV}}} - 2{{s}^{2}}\varphi {\kern 1pt} '{\kern 1pt} '\; + {{s}^{4}}\varphi = (\alpha + is{{v}^{{^{ \circ }}}})(\varphi {\kern 1pt} '{\kern 1pt} '\; - {{s}^{2}}\varphi ) - is{{v}^{{^{ \circ }}}}{\kern 1pt} '{\kern 1pt} '\varphi ,$

(2)

$\varphi (0) = \varphi (1) = 0,\quad \varphi {\kern 1pt} '(0) = \varphi {\kern 1pt} '(1) = 0$

для функции $\varphi (x) \in {{C}^{4}}(0;1)$. Как известно, задача (1), (2) моделирует развитие во времени возмущений, наложенных на стационарное плоскопараллельное сдвиговое течение с профилем продольной скорости $v^\circ (x) \in {{C}^{2}}(0;1)$ в плоском вязком слое, на границах x = 0 и x = 1 которого заданы условия прилипания к движущимся либо покоящимся стенкам. Все величины в (1) и (2) безразмерны, причем в размерный базис выбраны толщина слоя, плотность и динамическая вязкость. За счет такого выбора в левой части (1) отсутствует множитель 1/Re, обычно фигурирующий в литературе в записи уравнения Орра–Зоммерфельда.

Функция $\varphi $ связана с возмущением $\psi (x,y,t)$ функции тока соотношением

(3)

$\psi = \varphi (x){{{\text{e}}}^{{isy + \alpha t}}},\quad s > 0,\quad \alpha = {{\alpha }_{*}} + i{{\alpha }_{{**}}} \in C,$

где s – волновое число возмущения вдоль простирания слоя (вдоль оси y), $\alpha $ – комплексная частота колебаний в системе, являющаяся в задаче (1), (2) спектральным параметром. Критерий ограниченности (затухания к нулю) во времени отдельной гармоники возмущения с волновым числом $s$ – неположительность (отрицательность) всех действительных частот ${{\alpha }_{{*j}}}(s)$, $j = 1,2, \ldots $, соответствующих $s$. Если гармоники при всех $s > 0$ ограничены (затухают к нулю), то говорят об устойчивости (асимптотической устойчивости) сдвигового течения с профилем ${v}^\circ (x)$ относительно малых возмущений.

2. Обозначим через α₀ собственные числа задачи (1), (2) в простейшем случае $v^\circ (x) \equiv 0$, т.е. α₀ – комплексные частоты развития малых возмущений вблизи состояния покоя в слое. Непосредственной проверкой убедимся, что ${{\alpha }_{0}} \ne 0$. Действительно, при α = 0, $v^\circ \equiv 0$ анализ общего решения

(4)

$\varphi (x) = {{C}_{1}}{\text{ch}}\,sx + {{C}_{2}}{\text{sh}}\,sx + {{C}_{3}}sx\,{\text{ch}}\,sx + {{C}_{4}}sx\,{\text{sh}}\,sx$

уравнения (1) с условиями (2) дает однородную систему относительно ${{C}_{1}}$, ${{C}_{2}}$, ${{C}_{3}}$, ${{C}_{4}}$, имеющую только нулевое решение.

Итак, ${{\alpha }_{0}} \ne 0$. Тогда общее решение (1) имеет вид

(5)

$\begin{gathered} {{\varphi }_{0}}(x) = {{C}_{1}}{\text{ch}}\,sx + {{C}_{2}}{\text{sh}}\,sx + {{C}_{3}}{\text{ch}}\,\lambda x + {{C}_{4}}{\text{sh}}\,\lambda x, \\ {{\lambda }^{2}} = {{\alpha }_{0}} + {{s}^{2}}. \\ \end{gathered} $

Подстановка (5) в граничные условия (2) приводит к двум характеристическим уравнениям

(6)

$\frac{1}{\lambda }{\text{th}}\,\frac{\lambda }{2} = \frac{1}{s}{\text{th}}\,\frac{s}{2},\quad \lambda {\text{th}}\,\frac{\lambda }{2} = s{\text{th}}\,\frac{s}{2}.$

Объединение их решений $\lambda _{j}^{{(1)}}(s) = \lambda _{{j*}}^{{(1)}}(s) + i\lambda _{{j**}}^{{(1)}}(s)$ и $\lambda _{j}^{{(2)}}(s) = \lambda _{{j*}}^{{(2)}}(s) + i\lambda _{{j**}}^{{(2)}}(s)$, $j = 1,2, \ldots $, позволяет найти дисперсионные кривые ${{\alpha }_{0}}(s)$. В силу того, что ${{\alpha }_{0}} \ne 0$, очевидные действительные корни $\lambda = \pm s$ следует исключить из рассмотрения. Пользуясь монотонностью функций $y = \tfrac{{{\text{th}}x}}{x}$ и $y = x\,{\text{th}}x$ на интервалах x > 0 и x < 0, нетрудно показать, что других действительных корней у обоих уравнений (6) нет.

Характеристические уравнения (6) эквивалентны следующим двум системам относительно действительнозначных пар $(\lambda _{*}^{{(1)}},\lambda _{{**}}^{{(1)}})$ и $(\lambda _{*}^{{(2)}},\lambda _{{**}}^{{(2)}})$:

(7)

$\begin{gathered} {\text{th}}\,\frac{{\lambda _{*}^{{(1)}}}}{2} = \frac{1}{s}{\text{th}}\,\frac{s}{2}\left( {\lambda _{*}^{{(1)}} - \lambda _{{**}}^{{(1)}}{\text{th}}\,\frac{{\lambda _{*}^{{(1)}}}}{2}{\text{tg}}\,\frac{{\lambda _{{**}}^{{(1)}}}}{2}} \right), \\ {\text{tg}}\,\frac{{\lambda _{{**}}^{{(1)}}}}{2} = \frac{1}{s}{\text{th}}\,\frac{s}{2}\left( {\lambda _{{**}}^{{(1)}} + \lambda _{*}^{{(1)}}{\text{th}}\,\frac{{\lambda _{*}^{{(1)}}}}{2}{\text{tg}}\,\frac{{\lambda _{{**}}^{{(1)}}}}{2}} \right) \\ \end{gathered} $

(8)

$\begin{gathered} \lambda _{*}^{{(2)}}{\text{th}}\,\frac{{\lambda _{*}^{{(2)}}}}{2} - \lambda _{{**}}^{{(2)}}{\text{tg}}\,\frac{{\lambda _{{**}}^{{(2)}}}}{2} = s{\text{th}}\,\frac{s}{2}, \\ \lambda _{*}^{{(2)}}{\text{tg}}\,\frac{{\lambda _{{**}}^{{(2)}}}}{2} + \lambda _{{**}}^{{(2)}}{\text{th}}\,\frac{{\lambda _{*}^{{(2)}}}}{2} = s{\text{th}}\,\frac{s}{2}{\text{th}}\,\frac{{\lambda _{*}^{{(2)}}}}{2}{\text{tg}}\,\frac{{\lambda _{{**}}^{{(2)}}}}{2}. \\ \end{gathered} $

Не останавливаясь здесь на вычислительной проблеме отыскания всех пар решений систем (7) и (8), отметим пары, в которых $\lambda _{*}^{{(1)}} = 0$ и $\lambda _{*}^{{(2)}} = 0$, т.е. $\lambda _{j}^{{(1)}}(s) = i\lambda _{{j**}}^{{(1)}}(s)$ и $\lambda _{j}^{{(2)}}(s) = i\lambda _{{j**}}^{{(2)}}(s)$, где $\lambda _{{j**}}^{{(1)}}(s)$ и $\lambda _{{j**}}^{{(2)}}(s)$ – действительные корни уравнений

(9)

${\text{tg}}\,\frac{{\lambda _{{**}}^{{(1)}}}}{2} = \frac{{\lambda _{{**}}^{{(1)}}}}{s}{\text{th}}\;\frac{s}{2},\quad {\text{tg}}\,\frac{{\lambda _{{**}}^{{(2)}}}}{2} = - \frac{s}{{\lambda _{{**}}^{{(2)}}}}{\text{th}}\;\frac{s}{2}$

соответственно (s – параметр). Таким парам соответствуют два счетных набора действительных отрицательных частот

(10)

$\begin{gathered} {{\alpha }_{{0j}}}(s) = - {{(\lambda _{{j**}}^{{(1)}}(s))}^{2}} - {{s}^{2}}, \\ {{\alpha }_{{0j}}}(s) = - {{(\lambda _{{j**}}^{{(2)}}(s))}^{2}} - {{s}^{2}},\quad j = 1,2,\,\, \ldots \\ \end{gathered} $

Видно, что достаточно найти лишь положительные значения $\lambda _{{j**}}^{{(1)}}$ и $\lambda _{{j**}}^{{(2)}}$.

Анализ корней уравнений (9) показывает, что

(11)

$\lambda _{{j**}}^{{(1)}} \in (2j\pi ,2j\tilde {\lambda }),\quad \lambda _{{j**}}^{{(2)}} \in (2(j - 1)\pi ,2j\pi ),$

где $\tilde {\lambda } \approx 4.493$ – минимальный положительный корень уравнения ${\text{tg}}\,\tilde {\lambda } = \tilde {\lambda }$. Чем больше s, тем корни $\lambda _{{j**}}^{{(1)}}$ и $\lambda _{{j**}}^{{(2)}}$ ближе к левым границам своих интервалов, а чем ближе s к нулю, тем к правым.

Постоянные ${{C}_{1}}$, ${{C}_{2}}$, ${{C}_{3}}$, ${{C}_{4}}$ в (5) связаны таким образом, что вид собственной функции ${{\varphi }_{0}}(x)$ следующий:

(12)

$\begin{gathered} {{\varphi }_{0}}(x) = \frac{{\lambda {\text{sh}}\,s - s{\text{sh}}\,\lambda }}{{s(ch\,\lambda - ch\,s)}}(ch\,\lambda x - ch\,sx) + \\ \, + {\text{sh}}\,\lambda x - \frac{\lambda }{s}{\text{sh}}\,sx. \\ \end{gathered} $

3. Возвратимся к задаче (1), (2) и рассмотрим такие невозмущенные профили $v^\circ (x)$, что

(13)

$\mathop {sup}\limits_{0 < x < 1} {\text{|}}{{v}^{{^{ \circ }}}}{\text{|}} + \mathop {sup}\limits_{0 < x < 1} {\text{|}}{{v}^{{^{ \circ }}}}{\kern 1pt} '{\kern 1pt} '{\text{|}} \equiv \varepsilon \ll 1.$

Проведем регулярные разложения $\alpha \, = \,{{\alpha }_{0}}\, + \,\varepsilon {{\alpha }_{1}}$ + ..., $\varphi = {{\varphi }_{0}} + \varepsilon {{\varphi }_{1}}$ + ... собственных чисел α и собственных функций задачи (1), (2) по малому параметру ε. Здесь φ₀ определяется выражением (12), а $\lambda (s)$ и ${{\alpha }_{0}} = {{\lambda }^{2}} - {{s}^{2}}$ известны из рассмотренной ранее задачи об устойчивости состояния покоя в вязком слое.

В линейном по ε приближении для функции ${{\varphi }_{1}}(x)$ имеем неоднородное уравнение с постоянными коэффициентами

(14)

$\varphi _{1}^{{IV}} - ({{\alpha }_{0}} + 2{{s}^{2}})\varphi _{1}^{{''}} + {{s}^{2}}(\alpha _{0}^{2} + {{s}^{2}}){{\varphi }_{1}} = F(x),$

(15)

$F(x) = ({{\alpha }_{1}} + isV)(\varphi _{0}^{{''}} - {{s}^{2}}{{\varphi }_{0}}) - isV{\kern 1pt} '{\kern 1pt} '{{\varphi }_{0}},$

где $v^\circ (x) = \varepsilon V(x)$, $v^\circ {\kern 1pt} '{\kern 1pt} ' = \varepsilon V{\kern 1pt} '{\kern 1pt} '(x)$, $V(x) \sim 1$, а также аналогичные (2) граничные условия

(16)

${{\varphi }_{1}}(0) = {{\varphi }_{1}}(1) = 0,\quad \varphi _{1}^{'}(0) = \varphi _{1}^{'}(1) = 0.$

Неоднородность уравнения (14) формально не позволяет назвать задачу линейного по ε приближения (14), (16) задачей на собственные значения со спектральным параметром ${{\alpha }_{1}}$, входящим в правую часть (15).

Пользуясь (5), выпишем общее решение уравнения (14):

(17)

$\begin{gathered} {{\varphi }_{1}}(x) = {{D}_{1}}{\text{ch}}\,sx + {{D}_{2}}{\text{sh}}\,sx + {{D}_{3}}{\text{ch}}\,\lambda x + \\ \, + {{D}_{4}}{\text{sh}}\,\lambda x + {{\Phi }_{1}}(x,{{\alpha }_{1}}), \\ \end{gathered} $

где ${{\Phi }_{1}}(x,{{\alpha }_{1}})$ – какое-то из его частных решений. Подстановка (17) в (16) приводит к неоднородной системе линейных уравнений относительно ${{D}_{1}}$, ${{D}_{2}}$, ${{D}_{3}}$, ${{D}_{4}}$:

(18)

$\begin{gathered} {{D}_{1}} + {{D}_{3}} = - {{\Phi }_{1}}(0,{{\alpha }_{1}}),\quad s{{D}_{2}} + \lambda {{D}_{4}} = - \,\Phi _{1}^{'}(0,{{\alpha }_{1}}), \\ {{D}_{1}}{\text{ch}}\,s + {{D}_{2}}{\text{sh}}\,s + {{D}_{3}}{\text{ch}}\,\lambda + {{D}_{4}}{\text{sh}}\,\lambda = - \,{{\Phi }_{1}}(1,{{\alpha }_{1}}), \\ s{{D}_{1}}{\text{sh}}\,s + s{{D}_{2}}{\text{ch}}\,s + \lambda {{D}_{3}}{\text{sh}}\,\lambda + \lambda {{D}_{4}}{\text{ch}}\,\lambda = - \,\Phi _{1}^{'}(1,{{\alpha }_{1}}). \\ \end{gathered} $

Матрица однородной системы (18) заведомо вырождена (таковы корни λ характеристических уравнений (6)). Следовательно, существует тождественно нулевая нетривиальная линейная комбинация левых частей четырех равенств (18) с некоторыми постоянными ${{a}_{1}}$, ${{a}_{2}}$, ${{a}_{3}}$, ${{a}_{4}}$:

(19)

$\begin{gathered} {{a}_{1}}{{\Phi }_{1}}(0,{{\alpha }_{1}}) + {{a}_{2}}\Phi _{1}^{'}(0,{{\alpha }_{1}}) + \\ + {\kern 1pt} \,{{a}_{3}}{{\Phi }_{1}}(1,{{\alpha }_{1}}) + {{a}_{4}}\Phi _{1}^{'}(1,{{\alpha }_{1}}) = 0. \\ \end{gathered} $

Постоянные можно выбрать следующим образом:

(20)

$\begin{gathered} {{a}_{1}} = \frac{{\lambda {\text{sh}}\,\lambda {\text{ch}}\,s - s{\text{ch}}\lambda {\text{sh}}s}}{{{\text{ch}}\,\lambda - {\text{ch}}\,s}}, \\ {{a}_{2}} = \frac{{\lambda {\text{sh}}\,\lambda {\text{sh}}\,s - s({\text{ch}}\,\lambda {\text{ch}}\,s - 1)}}{{s({\text{ch}}\,\lambda - {\text{ch}}\,s)}}, \\ {{a}_{3}} = - \frac{{\lambda {\text{sh}}\,\lambda - s{\text{sh}}\,s}}{{{\text{ch}}\,\lambda - {\text{ch}}\,s}},\quad {{a}_{4}} = 1. \\ \end{gathered} $

Равенство (19) с учетом (20) служит алгебраическим уравнением для определения линейной составляющей ${{\alpha }_{1}}$ возмущения собственных чисел α.

4. Перейдем к аналитическому построению частного решения ${{\Phi }_{1}}(x,{{\alpha }_{1}})$. Представим уравнение (14) в операторном виде

(21)

с оператором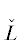

, определенным следующим образом:

(22)

Известно (см., например, [9, с. 376]), что уравнение 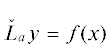с известной правой частью f имеет частное решение

(23)

$y(x) = \frac{1}{a}\int\limits_0^x \,f(\xi ){\text{sh}}\,[a(x - \xi )]d\xi .$

Повторно применяя формулу (23), найдем искомое частное решение уравнения (21):

(24)

${{\Phi }_{1}} = \frac{1}{{\lambda s}}\int\limits_0^x \,\int\limits_0^\xi \,F(\eta )\,{\text{sh}}\,[\lambda (\xi - \eta )]\,{\text{sh}}\,[s(x - \xi )]\,d\eta d\xi .$

После изменения порядка интегрирования по переменным $\xi $ и η в двойном интеграле (24) и вычисления внутреннего интеграла по $\xi $ получим одинарный интеграл по η:

(25)

$\begin{gathered} {{\Phi }_{1}} = \frac{1}{{\lambda s}}\int\limits_0^x \,\int\limits_\eta ^x \,F(\eta )\,{\text{sh}}\,[\lambda (\xi - \eta )]\,{\text{sh}}\,[s(x - \xi )]d\xi d\eta = \\ \, = \frac{1}{{\lambda s({{\lambda }^{2}} - {{s}^{2}})}}\int\limits_0^x \,F(\eta )\{ s{\text{sh}}\,[\lambda (x - \eta )] - \\ \, - \lambda {\text{sh}}\,[s(x - \eta )]\} d\eta , \\ \end{gathered} $

(26)

$\begin{gathered} \Phi _{1}^{'} = \frac{1}{{{{\lambda }^{2}} - {{s}^{2}}}}\int\limits_0^x \,F(\eta )\{ {\text{ch}}\,[\lambda (x - \eta )] - \\ \, - {\text{ch}}\,[s(x - \eta )]\} d\eta . \\ \end{gathered} $

Подставив выбранное частное решение (25), (26) в (19), окончательно вычислим представляющую основной интерес величину α₁:

(27)

${{\alpha }_{1}} = - is\frac{{\lambda s({\text{ch}}\,\lambda - {\text{ch}}\,s)\int\limits_0^1 \,\beta (\eta )A(\lambda ,s,\eta )d\eta - (\lambda {\text{sh}}\,\lambda - s{\text{sh}}\,s)\int\limits_0^1 \,\beta (\eta )B(\lambda ,s,\eta )d\eta }}{{\lambda s({\text{ch}}\,\lambda - {\text{ch}}\,s)\int\limits_0^1 \,\gamma (\eta )A(\lambda ,s,\eta )d\eta - (\lambda {\text{sh}}\,\lambda - s{\text{sh}}\,s)\int\limits_0^1 \,\gamma (\eta )B(\lambda ,s,\eta )d\eta }},$

где введены обозначения известных функций одного либо трех аргументов:

(28)

$\begin{gathered} \gamma (\eta ) = (\varphi _{0}^{{''}} - {{s}^{2}}{{\varphi }_{0}})(\eta ), \\ \beta (\eta ) = V(\eta )\gamma (\eta ) - V{\kern 1pt} '{\kern 1pt} '(\eta ){{\varphi }_{0}}(\eta ), \\ A(\lambda ,s,\eta ) = {\text{ch}}\,[\lambda (1 - \eta )] - {\text{ch}}\,[s(1 - \eta )], \\ B(\lambda ,s,\eta ) = s{\text{sh}}\,[\lambda (1 - \eta )] - \lambda {\text{sh}}\,[s(1 - \eta )]. \\ \end{gathered} $

Проведем краткий качественный анализ громоздкого выражения (27) в случае действительных отрицательных значений ${{\alpha }_{0}}$ (10). Им соответствуют корни $\lambda $, лежащие на мнимой оси. Из (28) видно, что в данном случае функция A действительна, а B принадлежит мнимой оси. Следовательно, ${{\alpha }_{{1*}}} = 0$. Таким образом, доказано следующее

Утверждение. Возмущения при малых в смысле меры (13) скоростях основного сдвига собственных значений, отвечающих монотонному затуханию вблизи состояния покоя в вязком слое, таковы, что вне зависимости от профиля скорости декремент затухания остается тем же, но появляется колебательная составляющая, по порядку малости на единицу меньшая этого декремента.

Подчеркнем общность при выборе скорости основного течения. Она может быть произвольной малой в смысле меры (13) функцией. Эта общность прослеживается вплоть до финального результата – выражений (27), (28) для возмущений собственных чисел.

5. Напомним, что в данной работе исследовались на возмущение дисперсионные кривые ${{\alpha }_{0}}(s)$, которым соответствовали только лежащие на мнимой оси комплексной плоскости λ корни характеристических уравнений (6). Представляет теоретический и прикладной интерес в дальнейшем провести вычислительный анализ для всех корней уравнений (6) или эквивалентных им алгебраических систем (7) и (8) относительно действительнозначных пар $(\lambda _{*}^{{(1)}},\lambda _{{**}}^{{(1)}})$ и $(\lambda _{*}^{{(2)}},\lambda _{{**}}^{{(2)}})$.

Список литературы

Orszag S.A. // J. Fluid Mech. 1971. V. 50. № 4. P. 689–703.
Miklavčič M. // Differential and Integral Equations. 1991. V. 4. № 4. P. 731–737.
Дубровский В.В., Кадченко С.И., Кравченко В.Ф., Садовничий В.А. // ДАН. 2001. Т. 378. № 4. С. 443–446.
Степин С.А. // Матем. сб. 1997. Т. 188. С. 129–146.
Туманов С.Н., Шкаликов А.А. // Изв. РАН. Сер. матем. 2002. Т. 66. № 4. С. 177–204.
Кадченко С.И., Торшина О.А., Рязанова Л.С. // Современные наукоемкие технологии. 2018. № 8. С. 89–94.
Веденеев В.В. Математическая теория устойчивости плоскопараллельных течений и развитие турбулентности. Долгопрудный: ИД “Интеллект”, 2016. 152 с.
Георгиевский Д.В. Избранные задачи механики сплошной среды. М.: ЛЕНАНД, 2018. 560 с.
Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Мир, 1971. 576 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал