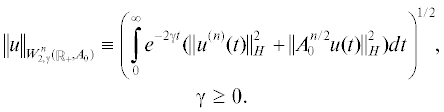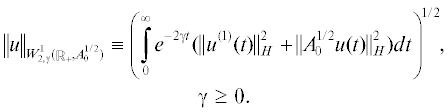Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 496, № 1, стр. 16-20
СПЕКТРАЛЬНЫЙ АНАЛИЗ И РАЗРЕШИМОСТЬ ВОЛЬТЕРРОВЫХ ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В. В. Власов 1, *, Н. А. Раутиан 1, **
1 Московский государственный университет
имени М.В. Ломоносова, Московский центр фундаментальной и прикладной математики
Москва, Россия
* E-mail: victor.vlasov@math.msu.ru
** E-mail: nadezhda.rautian@math.msu.ru
Поступила в редакцию 14.12.2020
После доработки 13.01.2021
Принята к публикации 18.01.2021
Аннотация
Работа посвящена исследованию интегро-дифференциальных уравнений с неограниченными операторными коэффициентами в гильбертовом пространстве. Изучаемые уравнения представляют собой абстрактные гиперболические уравнения, возмущенные слагаемыми, содержащими вольтерровы интегральные операторы. Эти уравнения являются операторными моделями интегро-дифференциальных уравнений с частными производными, возникающих в теории вязкоупругости, в теплофизике, в задачах усреднения в многофазных средах. Установлена корректная разрешимость указанных уравнений в весовых пространствах Соболева вектор-функций, а также проведен спектральный анализ оператор-функций, являющихся символами этих уравнений.
Интегро-дифференциальные уравнения с неограниченными операторными коэффициентами в гильбертовом пространстве могут быть реализованы как интегро-дифференциальные уравнения в частных производных, возникающие в теории вязкоупругости (см. [1–3]) а также как интегро-дифференциальные уравнения Гуртина–Пипкина (см. [4–7]), которые описывают процесс распространения тепла в средах с памятью с конечной скоростью, кроме того, указанные уравнения возникают в задачах усреднения в многофазных средах (закон Дарси) (см. [8]).
Перечисленные задачи можно объединить в достаточно широкий класс интегро-дифференциальных уравнений в частных производных, поэтому более естественно рассматривать интегро-дифференциальные уравнения с неограниченными операторными коэффициентами в гильбертовых пространствах (абстрактные интегро-дифференциальные уравнения), которые могут быть реализованы как интегро-дифференциальные уравнения в частных производных.
В наших предшествующих работах [7, 9, 10] проводилось подробное исследование задачи (1), (2) в случае, когда ядра интегральных операторов $K(t)$ и $Q(t)$ представимы в виде рядов убывающих экспонент с положительными коэффициентами, а также в случае, когда оператор B = 0. Наш подход к исследованию основан на спектральном анализе оператор-функции $L(\lambda )$, являющейся символом уравнения (1), который также дает возможность получить результат о корректной разрешимости и представление решения указанной задачи в виде ряда по экспонентам, соответствующим точкам спектра оператор-функции $L(\lambda )$. Указанные результаты подытожены в главе 3 монографии [7].
ОПРЕДЕЛЕНИЯ, ОБОЗНАЧЕНИЯ И ПОСТАНОВКА ЗАДАЧИ
Пусть H – сепарабельное гильбертово пространство, A – самосопряженный положительный оператор, $A{\kern 1pt} * = A \geqslant {{\kappa }_{0}}I$ $({{\kappa }_{0}} > 0)$, действующий в пространстве H, имеющий ограниченный обратный. Пусть B – симметрический оператор, $(Bx,y) = (x,By)$, действующий в пространстве H с областью определения $Dom(B)$ $(Dom(A) \subseteq Dom(B))$, неотрицательный $(Bx,x)$ ≥ 0, для любых x, $y \in Dom(B)$ и удовлетворяющий неравенству $\left\| {Bx} \right\| \leqslant \kappa \left\| {Ax} \right\|$, $0 < \kappa < 1$ для любого $x \in Dom\left( A \right)$, I – тождественный оператор в пространстве H.
Рассмотрим следующую задачу для интегро-дифференциального уравнения второго порядка на положительной полуоси ${{\mathbb{R}}_{ + }} = (0,\infty )$:
(1)
$\begin{gathered} \frac{{{{d}^{2}}u(t)}}{{d{{t}^{2}}}} + Au(t) + Bu(t) - \int\limits_0^t {K(t - s)Au(s)ds} - \\ \, - \int\limits_0^t {Q(t - s)Bu(s)ds} = f(t),\quad t \in {{\mathbb{R}}_{ + }}, \\ \end{gathered} $Предположим, что ядра интегральных операторов $K(t)$ и $Q(t)$ имеют следующее представление:
(4)
$K(t) = \int\limits_0^\infty {{{e}^{{ - t\tau }}}d\mu (\tau )} ,\quad Q(t) = \int\limits_0^\infty {{{e}^{{ - t\tau }}}d\eta (\tau )} ,$(5)
$\int\limits_0^\infty {\frac{{d\mu (\tau )}}{\tau }} < 1,\quad \int\limits_0^\infty {\frac{{d\eta (\tau )}}{\tau }} < 1,$(6)
$\begin{gathered} K(0) = \int\limits_0^\infty {d\mu (\tau )} \equiv \mathop {\left. {{\text{Var}}\mu } \right|}\nolimits_0^\infty < + \infty , \\ Q(0) = \int\limits_0^\infty {d\eta (\tau )} \equiv \mathop {\left. {{\text{Var}}\eta } \right|}\nolimits_0^\infty < + \infty , \\ \end{gathered} $Интегро-дифференциальное уравнение (1) представляет собой абстрактную форму динамического уравнения вязкоупругости (см. [1, 2]), где операторы A и B порождаются следующими дифференциальными выражениями:
Преобразование Лапласа сильного решения задачи (1), (2) с начальными условиями $u( + 0) = 0$, ${{u}^{{(1)}}}( + 0) = 0$ имеет следующее представление:
Здесь оператор-функция $L(\lambda )$ является символом уравнения (1) и имеет следующий вид:
где $\hat {K}(\lambda )$ и $\hat {Q}(\lambda )$ – преобразования Лапласа ядер $K(t)$ и $Q(t)$, соответственно, имеющие представления(9)
$\hat {K}(\lambda ) = \int\limits_0^\infty {\frac{{d\mu (\tau )}}{{\lambda + \tau }}} ,\quad \hat {Q}(\lambda ) = \int\limits_0^\infty {\frac{{d\eta (\tau )}}{{\lambda + \tau }}} ,$КОРРЕКТНАЯ РАЗРЕШИМОСТЬ
Согласно известному результату (теорема [14, с. 361]), оператор ${{A}_{0}}: = A + B$ является самосопряженным и положительным. Превратим область определения $Dom(A_{0}^{\beta })$ оператора $A_{0}^{\beta }$, β > 0 в гильбертово пространство Hβ, введя на $Dom(A_{0}^{\beta })$ норму ${{\left\| {\, \cdot \,} \right\|}_{\beta }} = {\text{||}}A_{0}^{\beta } \cdot \,{\text{||}}$, эквивалентную норме графика оператора $A_{0}^{\beta }$.
Через 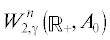 обозначим пространство Соболева вектор-функций на полуоси
обозначим пространство Соболева вектор-функций на полуоси 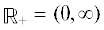 со значениями в H, снабженное нормой
со значениями в H, снабженное нормой
Подробнее о пространствах $W_{{2,\gamma }}^{n}\left( {{{\mathbb{R}}_{ + }},{{A}_{0}}} \right)$, см. монографию [12, глава 1]. При $n = 0$ полагаем $W_{{2,\gamma }}^{0}\left( {{{\mathbb{R}}_{ + }},{{A}_{0}}} \right) \equiv {{L}_{{2,\gamma }}}\left( {{{\mathbb{R}}_{ + }},H} \right)$, при γ = 0 будем писать $W_{{2,0}}^{n} = W_{2}^{n}$.
Определение 1. Будем называть вектор-функцию u сильным решением задачи (1)–(3), если она принадлежит пространству 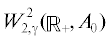 , для некоторого $\gamma \geqslant 0$, удовлетворяет уравнению (1) почти всюду на полуоси ${{\mathbb{R}}_{ + }}$ и начальному условию (2).
, для некоторого $\gamma \geqslant 0$, удовлетворяет уравнению (1) почти всюду на полуоси ${{\mathbb{R}}_{ + }}$ и начальному условию (2).
В нашей предшествующей работе [11] опубликована теорема о существовании и единственности сильного решения задачи (1)–(3).
Определение 2. Вектор-функцию u(t) ∈ ∈ $W_{{2,\gamma }}^{1}({{\mathbb{R}}_{ + }}$, $A_{0}^{{1/2}})$ назовем обобщенным (слабым) решением задачи (1)–(3), если $u\left( t \right)$ удовлетворяет интегральному тождеству
(10)
$\begin{gathered} \, - \mathop {\langle {{u}^{{(1)}}}(t),{{v}^{{(1)}}}(t)\rangle }\nolimits_{{{L}_{{2,\gamma }}}} + \\ + \,{{\langle {{(A\, + \,B)}^{{1/2}}}u(t),\mathop {(A\, + \,B)}\nolimits^{1/2} v(t)\rangle }_{{{{L}_{{2,\gamma }}}}}}\, + \,2\gamma \mathop {\langle {{u}^{{\left( 1 \right)}}}(t),v(t)\rangle }\nolimits_{{{L}_{{2,\gamma }}}} - \\ \, - \mathop {\left\langle {\int\limits_0^t \,\mathop {K(t\, - \,s)(A\, + \,B)}\nolimits^{ - 1/2} Au(s)ds,\mathop {(A\, + \,B)}\nolimits^{1/2} v(t)} \right\rangle }\nolimits_{{{L}_{{2,\gamma }}}} - \\ \, - {{\left\langle {\int\limits_0^t \,Q(t\, - \,s)\mathop {(A\, + \,B)}\nolimits^{ - 1/2} Bu(s)ds,\mathop {(A\, + \,B)}\nolimits^{1/2} {v}(t)} \right\rangle }_{{{{L}_{{2,\gamma }}}}}} - \\ - \,\mathop {\left\langle {f(t),v(t)} \right\rangle }\nolimits_{{{L}_{{2,\gamma }}}} - \left\langle {{{\varphi }_{1}},v\left( 0 \right)} \right\rangle = 0 \\ \end{gathered} $Отметим, что по определению пространства $W_{{2,\gamma }}^{1}({{\mathbb{R}}_{ + }},A_{0}^{{1/2}})$ вектор-функции ${{u}^{{(1)}}}(t)$ и $A_{0}^{{1/2}}u(t)$ принадлежат пространству ${{L}_{{2,{{\gamma }_{0}}}}}({{\mathbb{R}}_{ + }},H)$, поскольку норма в этом пространстве определяется следующим образом:
Следующая теорема дает нам достаточное условие корректной разрешимости задачи (1)–(3) в смысле определения 2.
Теорема 1. Пусть выполнено условие (6), $f(t) \in {{L}_{{2,{{\gamma }_{0}}}}}({{\mathbb{R}}_{ + }},H)$ для некоторого ${{\gamma }_{0}} \geqslant 0$, векторы ${{\varphi }_{0}} \in {{H}_{{1/2}}}$, ${{\varphi }_{1}} \in H$. Тогда существует такое ${{\gamma }_{1}} \geqslant {{\gamma }_{0}}$, что для любого $\gamma > {{\gamma }_{1}}$ задача (1)–(3) имеет обобщеное решение в пространстве $W_{{2,\gamma }}^{1}({{\mathbb{R}}_{ + }},A_{0}^{{1/2}})$, для которого справедлива следующая оценка:
(11)
$\mathop {\left\| u \right\|}\nolimits_{W_{{2,\gamma }}^{1}({{\mathbb{R}}_{ + }},A_{0}^{{1/2}})} \leqslant d\left( {\mathop {\left\| {f(t)} \right\|}\nolimits_{{{L}_{{2,\gamma }}}\left( {{{\mathbb{R}}_{ + }},H} \right)} + \,{\text{||}}A_{0}^{{1/2}}{{\varphi }_{0}}{\text{|}}{{{\text{|}}}_{H}} + \mathop {\left\| {{{\varphi }_{1}}} \right\|}\nolimits_H } \right),$Доказательство теоремы 1 существенно опирается на теорему о существовании и единственности сильного решения задачи (1)–(3) (см. [11, теорема 1]) и следующую лемму.
Лемма 1. При сделанных предположениях относительно операторов $A$ и $B$ справедливы неравенства
СПЕКТРАЛЬНЫЙ АНАЛИЗ
Перейдем к изучению структуры спектра оператор-функции $L(\lambda )$.
Теорема 2. Пусть выполнены условия (5), (6). Тогда спектр оператор-функции $L(\lambda )$ лежит в открытой левой полуплоскости $\left\{ {\lambda \in \mathbb{C}{\kern 1pt} :\;{\text{Re}}\lambda < 0} \right\}$.
Следующие теоремы 3 и 4 являются уточнением теорем 3 и 4 из нашей работы [11].
Теорема 3. Пусть выполнены условия (5), (6) и носители мер $\mu (\tau )$, $\nu (\tau )$ принадлежат отрезку $[{{d}_{1}}$, d2], где $(0 < {{d}_{1}} < {{d}_{2}} < + \infty )$. Тогда для любого сколь угодно малого ${{\theta }_{0}} > 0$ существует такое число ${{R}_{0}}$ > 0, что спектр оператор-функции $L(\lambda )$ принадлежит множеству
(14)
${{\alpha }_{2}} = - \frac{1}{2}\mathop {inf}\limits_{\left\| f \right\| = 1} \frac{{\left( {(K(0)A + Q(0)B)f,f} \right)}}{{\left( {(A + B + d_{2}^{2}I)f,f} \right)}}$При этом для оператор-функции ${{L}^{{ - 1}}}(\lambda )$ на множестве $\left\{ {\lambda {\kern 1pt} :\;{\text{Re}}\lambda < - {{R}_{0}}} \right\}$ ∪ $\left\{ {\lambda {\kern 1pt} :\;{\text{Re}}\lambda > 0} \right\}$ справедлива оценка
(15)
$\left\| {{{L}^{{ - 1}}}(\lambda )} \right\| \leqslant \frac{{{\text{const}}}}{{\left| \lambda \right|\left| {{\text{Re}}\lambda } \right|}}.$Теорема 4. Пусть выполнены условия теоремы 3. Тогда невещественная часть спектра оператор-функции $L(\lambda )$ симметрична относительно вещественной оси и состоит из собственных значений конечной алгебраической кратности, причем для любого $\varepsilon > 0$ в области Ωε := $\Omega {\backslash }\left\{ {\lambda \in \mathbb{C}:{\text{|Im}}\lambda {\text{|}} < \varepsilon } \right\}$ собственные значения являются изолированными, т.е. не имеют точек накопления.
Замечание 1. Отметим, что оператор-функция вида (8) в случае, когда ядра интегральных операторов K(t) и Q(t) представимы в виде суммы конечного числа убывающих экспонент с положительными коэффициентами, изучалась А.И. Милославским в работе [13]. Исследование оператор-функции вида (8) в случае, когда ядра интегральных операторов K(t) и Q(t) представимы в виде рядов убывающих экспонент с положительными коэффициентами, проводилось в работах [9, 10], соответствующие результаты содержатся также в монографии [7]. При этом в статье [10] получено обобщение некоторых результатов работы [13]. Теоремы 3, 4 представляют собой естественное развитие результатов, изложенных в монографии в [7], и обобщение соответствующих результатов, полученных в работе [13].
Обозначим через $N\left( {\mu ;L\left( \lambda \right)} \right)$ кратность характеристического числа λ = μ оператор-функции L(λ). Введем $\nu \left( {r;\Omega ;L\left( \lambda \right)} \right)$ – функцию распределения характеристических чисел оператор-функции L(λ). Предполагая L(λ) аналитической оператор-функцией в области $\Omega $, положим
Причем, если в области $\Omega \cap \left\{ {\lambda {\kern 1pt} :\;\left| \lambda \right| < r} \right\}$ лежит бесконечное число характеристических чисел L(λ) либо $N\left( {\mu ;L\left( \lambda \right)} \right) = \infty $ хотя бы в одной точке $\mu \in \Omega $ с $\left| \mu \right| < r$, то
Обозначим область ${{\Psi }_{{\theta ,\eta }}} = \{ \lambda {\kern 1pt} :\;{\text{|}}\lambda {\text{|}} > \eta ,{\text{|}}arg\lambda {\text{|}} < \theta \} $, $\pi {\text{/}}2$ < θ < π, причем здесь $ - \pi < arg\lambda \leqslant \pi .$ В дальнейшем соотношение ${{\nu }_{1}}(t) \sim {{\nu }_{2}}(t)$ означает, что $\frac{{{{\nu }_{1}}(t)}}{{{{\nu }_{2}}(t)}} \to 1$ при $t \to \infty .$
Следуя [15], через $\Re $ обозначим множество таких неубывающих функций ν(r), определенных при достаточно больших вещественных r, что для каждой функции $\nu \left( r \right) \in \Re $ существует постоянная a > 1, для которой $\nu \left( {ar} \right) \geqslant 2\nu \left( r \right)$ при достаточно больших r. Пусть $\Im $ – множество неубывающих функций ν(r), обладающих свойством: для каждого $\varepsilon > 0$ найдется такое $\delta > 0$, что
Обозначим через $P\left( \lambda \right)$ оператор-функцию вида
Используя теорему 2.1 [15] и теорему 3, получаем следующий результат.
Теорема 5. Пусть выполнены условия теоремы 3, $\nu \left( {r;{{\Psi }_{{\theta ,\eta }}};P\left( \lambda \right)} \right) \in \Re \cap \Im .$ Тогда спектр оператор-функции $L\left( \lambda \right)$ в области ${{\Psi }_{{\theta ,\eta }}}$ состоит из дискретных точек спектра и справедливо равенство
Список литературы
Ильюшин А.А., Победря Б.Е. Основы математической теории термовязкоупругости. М.: “Наука”, 1970. 280 с.
Christensen R.M. Theory of viscoelasticity. An introduction. N.Y.; L.: Academic Press, 1971. 364 p.
Amendola G., Fabrizio M., Golden J.M. Thermodynamics of Materials with memory.Theory and applications. N.Y.; Dordrecht; Heidelberg; London: Springer, 2012. 576 p.
Gurtin M.E., Pipkin A.C. General theory of heat conduction with finite wave speed // Arch. Rat. Mech. Anal. 1968. V. 31. P. 113–126.
Лыков А.В. Тепломассообмен: (Справочник). 2-е изд., перераб. и доп. М.: Энергия, 1978. 480с.
Eremenko A., Ivanov S. Spectra of the Gurtin-Pipkin type equations // SIAM J. Math. Anal. 2011. V. 43. № 5. P. 2296–2306.
Власов В.В., Раутиан Н.А. Спектральный анализ функционально-дифференциальных уравнений. М.: МАКС Пресс, 2016. 488 с. ISBN 978-5-317-05443-4.
Санче-Паленсия Э. Неоднородные среды и теория колебаний. М.: Мир, 1984. 472 с.
Власов В.В., Раутиан Н.А. Спектральный анализ гиперболических вольтерровых интегродифференциальных уравнений // ДАН. 2015. Т. 464. № 6. С. 656–660.
Власов В.В., Раутиан Н.А. Корректная разрешимость и спектральный анализ интегродифференциальных уравнений, возникающих в теории вязкоупругости // Современная математика. Фундаментальные направления. 2015. Т. 58. С. 22–42.
Власов В.В., Раутиан Н.А. Исследование вольтерровых интегро-дифференциальных уравнений, возникающих в теории вязкоупругости // ДАН. 2016. Т. 471. № 3. С. 259–262.
Лионс Ж.П., Мадженес Э. Неоднородные граничные задачи и их приложения. М.: Мир, 1971. 371 с.
Милославский А.И. Спектральные свойства операторного пучка, возникающего в вязкоупругости // Деп. в Укр. НИИНТИ. 13.07.87. № 1229-УК87. Харьков, 1987. 53 с.
Като Т. Теория возмущений линейных операторов. М.: Мир, 1972. 740 с.
Радзиевский Г.В. Асимптотика распределения характеристических чисел оператор-функций, аналитических в угле // Матем. сб. 1980. Т.112. № 3. С. 396–420.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления