1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 498, № 1, 2021

Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 498, № 1, стр. 59-64

МОДЕЛИРОВАНИЕ СЕЙСМИЧЕСКИХ ВОЛН В АНИЗОТРОПНЫХ СРЕДАХ

Член-корреспондент РАН И. Б. Петров 1, *, В. И. Голубев 1, 2, **, В. Ю. Петрухин 1, И. С. Никитин 2

1 Московский физико-технический институт (национальный исследовательский университет)
Долгопрудный, Московская обл., Россия

2 Институт автоматизации проектирования Российской академии наук
Москва, Россия

* E-mail: petrov@mipt.ru
** E-mail: w.golubev@mail.ru

Поступила в редакцию 26.02.2021
После доработки 26.02.2021
Принята к публикации 24.03.2021

Полный текст (PDF)

Аннотация

Рассматривается задача о распространении сейсмических волн в гетерогенном геологическом массиве. Для описания динамического поведения среды используются уравнения линейной теории упругости. Учет слоистой структуры массива производится на основе поперечно-изотропной модели геологического разреза. Для численного решения определяющей системы уравнений используется сеточно-характеристический метод на параллелепипедных сетках. Авторами реализован подход, позволяющий в явном виде решить контактную задачу между изотропной и анизотропной средами. Представлен алгоритм, позволяющий провести полноволновое моделирование всех типов поверхностных и объемных волн. Его работоспособность подтверждена на примере анизотропной модели Marmousi II.

Ключевые слова: математическое моделирование, сеточно-характеристический метод, сейсморазведка, анизотропная среда, сейсмические волны

Первые сейсмические методы поиска и разведки месторождений полезных ископаемых появились более 100 лет назад. За эти годы сейсмическая разведка стала одним из ведущих геофизических методов. Основанная изначально на простейшем лучевом представлении о распространении сейсмических волн, сегодня она использует все более сложные и реалистичные модели динамического поведения геологических сред [1–4]. При этом повышение точности восстановления внутренней структуры среды наиболее важно для залежей нетрадиционных углеводородов. Полученные оценки используются для оптимизации схемы разработки месторождений. Ввиду невозможности проведения натурных полномасштабных экспериментальных исследований геологических структур с заданной геометрией на практике активно применяются математическое моделирование и численный эксперимент.

Хорошие обзоры современных методов вычислительной физики, применяемых для решения задач о распространении сейсмических волн, представлены в работах [5–7]. При этом, ввиду гиперболичности волновой задачи, естественным является применение класса сеточно-характеристических методов [8], учитывающих распространение разрывов решения вдоль характеристик. Они доказали свою эффективность при решении задач акустики [9] и упругости [10], а также динамики трещиноватых [11] и нелинейных слоистых сред [12].

В настоящей работе рассматривается задача динамической нагрузки гетерогенного геологического массива. Целью исследования является построение вычислительного алгоритма, позволяющего учитывать тонкослоистую структуру отдельных криволинейных геологических слоев. В работе используется модель поперечно-изотропной линейно-упругой среды в двумерной постановке. Для нахождения численного решения на первом шаге используется расщепление по пространственным направлениям. В дальнейшем отдельные одномерные линейные уравнения переноса решаются сеточно-характеристическим методом повышенного порядка точности. Для верификации построенного алгоритма используются результаты расчетов в однородных средах, представленные в работе [13]. В работе описан алгоритм, позволяющий построить точное решение на контакте изотропная–анизотропная среды, основанный на аналитическом решении задачи Римана о распаде разрыва [14]. Проведено сопоставление полученных полей смещений. Разработанный расчетный алгоритм успешно применен для решения задачи о точечном источнике в сложно построенной горизонтально-изотропной модели, основанной на изотропной упругой модели Marmousi II [15].

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Уравнения, описывающие динамическое поведение бесконечно малого объема изотропной линейно-упругой среды, могут быть записаны в виде

(1)
$\rho \frac{\partial }{{\partial t}}{\mathbf{v}} = \nabla \cdot \sigma ,$
(2)
$\frac{\partial }{{\partial t}}\sigma = \lambda (\nabla \cdot {\mathbf{v}})I + \mu (\nabla \otimes {\mathbf{v}} + {\mathbf{v}} \otimes \nabla ),$
где ρ – плотность среды, σ – тензор напряжений, v – вектор скорости среды, λ и μ – упругие параметры Ламе.

Ввиду особенностей формирования (осадконакопление и эрозия) реальные геологические среды являются поперечно-изотропными (VTI). Для них связь между тензором напряжений $\sigma $ и тензором деформаций ε выражается следующим реологическим соотношением (в двумерной постановке):

(3)
$\left( {\begin{array}{*{20}{c}} {{{\sigma }_{{xx}}}} \\ {{{\sigma }_{{yy}}}} \\ {{{\sigma }_{{xy}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{C}_{{11}}}}&{{{C}_{{13}}}}&0 \\ {{{C}_{{13}}}}&{{{C}_{{33}}}}&0 \\ 0&0&{{{C}_{{44}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{\varepsilon }_{{xx}}}} \\ {{{\varepsilon }_{{yy}}}} \\ {{{\varepsilon }_{{xy}}}} \end{array}} \right),$
где Cij – упругие параметры среды, а ось OY направлена вертикально.

Система уравнений в частных производных первого порядка (1)–(3) может быть приведена к каноническому виду:

(4)
$\frac{\partial }{{\partial t}}{\mathbf{q}} + {{A}_{x}}\frac{\partial }{{\partial x}}{\mathbf{q}} + {{A}_{y}}\frac{\partial }{{\partial y}}{\mathbf{q}} = {\mathbf{f}},$
где ${\mathbf{q}} = {{\left( {\begin{array}{*{20}{c}} {{{{v}}_{x}}}&{{{{v}}_{y}}}&{{{\sigma }_{{xx}}}}&{{{\sigma }_{{yy}}}}&{{{\sigma }_{{xy}}}} \end{array}} \right)}^{T}}$ – вектор неизвестных функций, f – источник сейсмического сигнала, а матрицы Ax и Ay имеют вид

(5)
${{A}_{x}} = - \left( {\begin{array}{*{20}{c}} 0&0&{{{\rho }^{{ - 1}}}}&0&0 \\ 0&0&0&0&{{{\rho }^{{ - 1}}}} \\ {{{C}_{{11}}}}&0&0&0&0 \\ {{{C}_{{13}}}}&0&0&0&0 \\ 0&{{{C}_{{44}}}}&0&0&0 \end{array}} \right),$
(6)
${{A}_{y}} = - \left( {\begin{array}{*{20}{c}} 0&0&0&0&{{{\rho }^{{ - 1}}}} \\ 0&0&0&{{{\rho }^{{ - 1}}}}&0 \\ 0&{{{C}_{{13}}}}&0&0&0 \\ 0&{{{C}_{{33}}}}&0&0&0 \\ {{{C}_{{44}}}}&0&0&0&0 \end{array}} \right).$

Обе представленные матрицы могут быть записаны в виде $A = {{{{\Omega }}}^{{ - 1}}}{{\Lambda \Omega }}$, где матрица Ω состоит из собственных векторов, а Λ – из соответствующих им собственных значений. Отличные от нуля собственные значения равны $ \pm \sqrt {\frac{{{{C}_{{11}}}}}{\rho }} , \pm \sqrt {\frac{{{{C}_{{33}}}}}{\rho }} , \pm \sqrt {\frac{{{{C}_{{44}}}}}{\rho }} $, что обусловливает зависимость скорости распространения сейсмических волн от направления.

Обе приведенные выше системы уравнений являются гиперболическими, и после проведения расщепления по направлениям каждая из них может быть решена сеточно-характеристическим методом с переходом в инварианты Римана и обратно. При этом устойчивость полученного вычислительного алгоритма определяется критерием Куранта–Фридрихса–Леви. Порядок аппроксимации схемы совпадает с порядком восстанавливаемого интерполяционного полинома в одномерном случае и снижается до второго в двумерном случае из-за расщепления по направлениям.

Рассмотрим подробнее случай контакта между изотропной и горизонтально-изотропной (анизотропной) средами, который может реализовываться, например, при детальном описании строения верхней части разреза и более грубом описании объема нефтяной залежи. На границе между средами должно быть задано необходимое число контактных условий – по количеству выходящих из сред на границу характеристик. Таким образом, в рассматриваемом нами случае достаточно четырех условий. Они формулируются в следующем виде:

(7)
${{{\mathbf{v}}}^{i}} = {{{\mathbf{v}}}^{a}},$
(8)
${{\sigma }^{i}} \cdot {\mathbf{n}} = {{\sigma }^{a}} \cdot {\mathbf{n}},$
где vi – вектор скорости изотропной среды, va – вектор скорости анизотропной среды, ${{\sigma }^{i}}$ – тензор напряжений изотропной среды, ${{\sigma }^{a}}$ – тензор напряжений анизотропной среды, n – нормаль, направленная из изотропной среды в анизотропную среду.

В настоящей работе был развит подход, предложенный в работе [10] для изотропной упругой среды. Корректировочные формулы, обеспечивающие точное равенство скорости точек на границе расчетной области заданному вектору ${{{\mathbf{V}}}^{{ext}}}$, имеют вид

(9)
${{\sigma }_{{xx}}} - = \pm \sqrt {\rho {{C}_{{11}}}} ({{{v}}_{x}} - V_{x}^{{ext}}),$
(10)
${{\sigma }_{{yy}}} - = \pm {{C}_{{13}}}\sqrt {\frac{\rho }{{{{C}_{{11}}}}}} ({{{v}}_{x}} - V_{x}^{{ext}}),$
(11)
${{\sigma }_{{xy}}} - = \pm \sqrt {\rho {{C}_{{44}}}} ({{{v}}_{y}} - V_{y}^{{ext}}),$
(12)
${\mathbf{v}} = {{{\mathbf{V}}}^{{ext}}},$
если нормаль к границе совпадает с горизонтальной осью, и
(13)
${{\sigma }_{{xx}}} - = \pm {{C}_{{13}}}\sqrt {\frac{\rho }{{{{C}_{{33}}}}}} ({{{v}}_{y}} - V_{y}^{{ext}}),$
(14)
${{\sigma }_{{yy}}} - = \pm \sqrt {\rho {{C}_{{33}}}} ({{{v}}_{y}} - V_{y}^{{ext}}),$
(15)
${{\sigma }_{{xy}}} - = \pm \sqrt {\rho {{C}_{{44}}}} ({{{v}}_{x}} - V_{x}^{{ext}}),$
(16)
${\mathbf{v}} = {{{\mathbf{V}}}^{{ext}}},$
если нормаль к границе совпадает с вертикальной осью. Здесь знак плюс соответствует положительно направленной нормали, а знак минус – отрицательно направленной нормали. Тогда из условий (7)–(8) может быть найден такой вектор ${{{\mathbf{V}}}^{{ext}}}$, использование которого в граничном корректоре обеспечит точное выполнение физических условий на контакте двух разнородных сред. Если внешняя нормаль к анизотропной среде направлена вдоль оси OX:
(17)
$V_{x}^{{ext}} = \frac{{ \pm (\sigma _{{xx}}^{i} - \sigma _{{xx}}^{a}) + \sqrt {{{\rho }^{a}}{{C}_{{11}}}} {v}_{x}^{a} + \sqrt {{{\rho }^{i}}\left( {\lambda + 2\mu } \right)} {v}_{x}^{i}}}{{\sqrt {{{\rho }^{a}}{{C}_{{11}}}} + \sqrt {{{\rho }^{i}}\left( {\lambda + 2\mu } \right)} }},$
(18)
$V_{y}^{{ext}} = \frac{{ \pm (\sigma _{{xy}}^{i} - \sigma _{{xy}}^{a}) + \sqrt {{{\rho }^{a}}{{C}_{{44}}}} {v}_{y}^{a} + \sqrt {{{\rho }^{i}}\mu } {v}_{y}^{i}}}{{\sqrt {{{\rho }^{a}}{{C}_{{44}}}} + \sqrt {{{\rho }^{i}}\mu } }},$
и вдоль оси OY:
(19)
$V_{x}^{{ext}} = \frac{{ \pm (\sigma _{{xy}}^{i} - \sigma _{{xy}}^{a}) + \sqrt {{{\rho }^{a}}{{C}_{{44}}}} {v}_{x}^{a} + \sqrt {{{\rho }^{i}}\mu } {v}_{x}^{i}}}{{\sqrt {{{\rho }^{a}}{{C}_{{44}}}} + \sqrt {{{\rho }^{i}}\mu } }},$
(20)
$V_{y}^{{ext}} = \frac{{ \pm (\sigma _{{yy}}^{i} - \sigma _{{yy}}^{a}) + \sqrt {{{\rho }^{a}}{{C}_{{33}}}} {v}_{y}^{a} + \sqrt {{{\rho }^{i}}\left( {\lambda + 2\mu } \right)} {v}_{y}^{i}}}{{\sqrt {{{\rho }^{a}}{{C}_{{33}}}} + \sqrt {{{\rho }^{i}}\left( {\lambda + 2\mu } \right)} }},$
где знак плюс соответствует положительно направленной нормали, а знак минус – отрицательно направленной нормали.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

В работе было выполнено тестирование разработанного алгоритма на задаче о точечном источнике, расположенном в двух материалах, значительно отличающихся параметрами анизотропии. В обоих случаях расчетная область представляла собой квадрат размерами 33 × 33 см. Была построена расчетная сетка с шагом 2 × 2 мм. Шаг по времени выбирался из условия устойчивости и составлял 0.1 мкс. При решении отдельных уравнений переноса на инварианты Римана использовалась схема Русанова с монотонизатором minimax третьего порядка точности. В качестве источника возмущения использовался точечный источник вертикально направленной силы, приложенный в центре расчетной области и имеющий временную зависимость вида

(21)
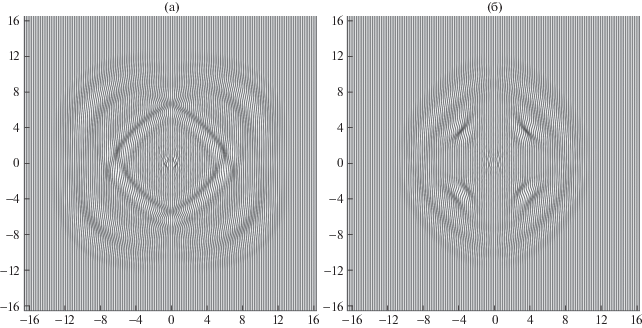
$f\left( t \right) = {{e}^{{ - 0.5f_{0}^{2}{{{\left( {t - {{t}_{0}}} \right)}}^{2}}}}}\cos \pi {{f}_{0}}\left( {t - {{t}_{0}}} \right),$
с параметрами ${{f}_{0}} = 5 \times {{10}^{5}}$ Гц, ${{t}_{0}} = 6$ мкс. В первом расчете использовался апатит с параметрами ${{C}_{{11}}} = 16.7 \times {{10}^{{10}}}~\,\,{\text{Н/м}}$, ${{C}_{{13}}} = 6.6 \times {{10}^{{10}}}~\,\,{\text{Н/м}}$, С33 = = 14.0 ×  $~{{10}^{{10}}}~\,\,{\text{Н/м}}$, $~{{C}_{{44}}} = 6.63 \times {{10}^{{10}}}\,\,~{\text{Н/м}}$, $~~\rho = $ = $~3200\,\,{\text{кг/}}{{{\text{м}}}^{3}}$. Им соответствуют следующие скорости    распространения волн: 7224, 4551 и  6614 м/с. Во втором расчете использовался кобальт     с параметрами ${{C}_{{11}}} = 30.7 \times {{10}^{{10}}}~\,\,{\text{Н/м}},$ ${{C}_{{13}}} = 10.3\,\,\, \times \,\,\,{{10}^{{10}}}~\,\,{\text{Н/м}}$, C33 = 35.8 ×  ${{10}^{{10}}}\,\,~{\text{Н/м}}$, ${{C}_{{44}}} = 7.55 \times {{10}^{{10}}}\,\,~{\text{Н/м}},\,\,\rho = 8900\,\,~{\text{кг/}}{{{\text{м}}}^{3}}$. Им соответствуют следующие скорости распространения волн: 5873, 2912 и 6342 м/с. На границах области моделирования использовались неотражающие граничные условия. В расчетах записывались обе компоненты скорости смещения среды во всех узлах расчетной сетки. В дальнейшем, на основе полученных данных, вычислялось поле горизонтальных смещений путем интегрирования сигнала по времени. Для обоих расчетов результаты представлены на рис. 1. Они полностью совпали с результатами, представленными в работе [9], в которой использовался псевдоспектральный метод.

Рис. 1.

Поле смещений ux, рассчитанное в апатите через 20 мкс после начала воздействия (а). Поле смещений ux, рассчитанное в кобальте через 24 мкс после начала воздействия (б).

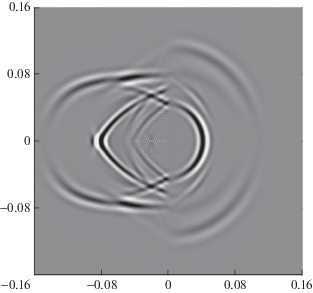
Представленный в работе метод позволяет в явном виде находить решение динамической задачи о контакте изотропной и анизотропной сред. Была рассмотрена следующая постановка задачи. Левая половина расчетной области заполнена цинком с параметрами C11 = 16.5 × × ${{10}^{{10}}}\,~{\text{Н/м}},{{C}_{{13}}} = 5.0 \times {{10}^{{10}}}\,~{\text{Н/м}}$, C33 = 6.2 × 1010${\text{Н/м}}$, ${{C}_{{44}}} = 3.96 \times {{10}^{{10}}}\,\,{\text{Н/м}},\,\,~\rho = 7100\,\,~{\text{кг/}}{{{\text{м}}}^{3}}$. Им соответствуют следующие скорости распространения волн: 4820, 2361 и 2955 м/с. Правая половина расчетной области заполнена изотропным материалом, обладающим такой же плотностью, скоростью распространения продольных волн 4820 м/с и скоростью распространения поперечных волн 2361 м/с. Вблизи контактной границы в анизотропном материале задавался точечный источник вертикальной силы с временной зависимостью (21). Вся расчетная область имела размеры 32 × 32 см, пространственный шаг сетки составлял 0.8 мм, временной шаг был равен 0.1 мкс. На рис. 2 представлена волновая картина, построенная по вертикальной компоненте вектора смещений. Четко видны  изотропия расходящейся волны справа и вытянутая пространственная форма сигнала слева.

Рис. 2.

Поле смещений uy, рассчитанное при контакте цинка (левая половина) и изотропной среды (правая половина) через 32 мкс после начала воздействия.

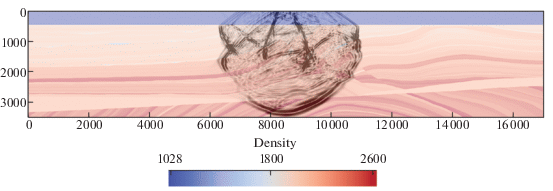
В работе был проведен численный расчет распространения сейсмических волн в реалистичной модели сложно построенного геологического массива. За основу была взята свободно распространяемая упругая модель Marmousi II. В нее была внесена VTI анизотропия с использованием следующих соотношений:

(22)
$\varepsilon = 0.25\rho - 0.3,$
(23)
$\delta = 0.125\rho - 0.1,$
(24)
${{C}_{{11}}} = \rho \left( {1 + 2\varepsilon } \right)V_{P}^{2},$
(25)
${{C}_{{33}}} = \rho V_{P}^{2},$
(26)
${{C}_{{44}}} = \rho V_{S}^{2},$
(27)
${{C}_{{13}}} = \rho V_{P}^{2}\sqrt {\left( {1 - \frac{{V_{S}^{2}}}{{V_{P}^{2}}}} \right)\left( {1 - \frac{{V_{S}^{2}}}{{V_{P}^{2}}} + 2\delta } \right)} - \rho V_{S}^{2},$
где плотность рассчитывается в г/см3, а ε и δ – параметры Томсена.

Для покрытия модели расчетной сеткой был выбран шаг по пространству 5 м и 3401 × 701 узлов. Шаг по времени определялся условием Куранта и составлял 0.8 мс. В каждой ячейке расчетной сетки хранились все параметры анизотропного материала. В качестве возмущения использовался точечный источник (центр давления), расположенный вблизи дневной поверхности. На рис. 3 представлено распределение модуля скорости в фиксированный момент времени. Слоистость геологической модели, наличие резких границ и анизотропия обусловливают сложную волновую картину.

Рис. 3.

Распределение модуля скорости в анизотропной модели Marmousi II в фиксированный момент времени.

ЗАКЛЮЧЕНИЕ

В работе представлен подход, позволяющий проводить учет VTI анизотропии при математическом моделировании процесса распространения сейсмических волн в геологическом массиве. Построена явная разностная схема, основанная на расщеплении по пространственным направлениям и сеточно-характеристическом методе. Предложен способ, позволяющий обеспечить выполнение контактных условий на границе изотропной и анизотропной сред. Корректность вычислительного алгоритма была подтверждена сопоставлением полученного решения для однородной и неоднородной сред. Был проведен расчет процесса распространения сейсмических волн в VTI модели Marmousi II. Неоднородность геологического строения среды обусловливает сложную волновую картину объемных волн. Дальнейшее развитие идей, изложенных в работе, может быть направлено на их обобщение на трехмерный случай и учет трещиноватости анизотропной среды.

Список литературы

  1. Carcione J.M., Morency C., Santos J.E. Computational poroelasticity – A review // Geophysics. 2010. V. 75. A229-A243.

  2. Ba J., Carcione J.M., Cao H., Yao F., Du Q. Poro-acoustoelasticity of fluid-saturated rocks // Geophys. Prosp. 2012. V. 61. P. 599–612.

  3. Gauzellino P., Carcione J.M., Santos J.E., Picotti S. A rheological equation for anisotropic-anelastic media and simulation of synthetic seismograms // Wave Motion. 2014. V. 51. P. 743–757.

  4. Carcione J.M., Wang Z., Ling W., Salusti E., Ba J., Fu L.-Y. Wave simulation in linear thermoelastic media // Geophysics. 2019. V. 84 (1). T1–T11.

  5. Virieux J., Calandra H., Plessix R.E. A review of the spectral, pseudo-spectral, finite-difference and finite-element modelling techniques for geophysical imaging // Geophysical Prospecting. 2011. V. 59 (5). P. 794–813.

  6. Carcione J.M., Herman C.G., Kroode P.E. Y2K Review Article: Seismic Modeling // Rev. Lit. Arts Amer. 2002. V. 67 (4). P. 1304–1325.

  7. Jing Ba et al. Seismic Exploration of Hydrocarbons in Heterogeneous Reservoirs: New Theories, Methods and Applications. Elsevier, 2015. 362 p.

  8. Холодов А.С. О построении разностных схем повышенного порядка точности для уравнений гиперболического типа // ЖВМиМФ. 1980. Т. 20. № 6. С. 1601–1620.

  9. Петров И.Б., Голубев В.И., Шевченко А.В. О задаче акустической диагностики прискважинной зоны // Доклады РАН. Математика, информатика, процессы управления. 2020. Т. 492. № 1. С. 92–96.

  10. Favorskaya A., Golubev V. Study the elastic waves propagation in multistory buildings, taking into account dynamic destruction // Smart Innovation, Systems and Technologies. 2020. V. 193. P. 189–199.

  11. Golubev V., Nikitin I., Ekimenko A. Simulation of seismic responses from fractured MARMOUSI2 model // AIP Conference Proceeding. 2020. 2312, № 050006.

  12. Golubev V., Nikitin I., Golubeva Yu., Petrov I. Numerical simulation of the dynamic loading process of initially damaged media // AIP Conf. Proc. 2020. 2309, 020006 https://doi.org/10.1063/5.0033949

  13. Carcione J.M., Kosloff D., Kosloff R. Wave propagation simulation in an anisotropic (transversely isotropic) medium // Quart. Journ. Mech. Appl. Math. 1988. V. 41. P. 320–345.

  14. Golubev V., Shevchenko A., Petrov I. Simulation of Seismic Wave Propagation in a Multicomponent Oil Deposit Model // Intern. J. Appl. Mech. 2020. V. 12 (8). № 2050084.

  15. Qingyang Li, Guochen Wu, Jianlu Wu, Peiran Duan. Finite difference seismic forward modeling method for fluid–solid coupled media with irregular seabed interface // J. Geophysics and Engineering. 2019. V. 16. № 1. P. 198–214.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал