Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 501, № 1, стр. 52-56

ВВЕДЕНИЕ

Система уравнений

где носит имя Ферми–Паста–Улама. Она была предложена в [1]. Здесь $M > 0$, индекс $j$ меняется от $1$ до $N$ и выполнены условия “периодичности”: ${{u}_{0}} \equiv {{u}_{N}},{{u}_{{N + 1}}} \equiv {{u}_{1}}$. Значения ${{u}_{j}}(t)$ можно ассоциировать со значениями функции двух переменных $u(t,{{x}_{j}})$ в равномерно распределенных на некоторой окружности точках с угловой координатой ${{x}_{j}}$. Основное предположение настоящей работы состоит в том, что значение $N$ достаточно велико, т.е. величина $\varepsilon = 2\pi {{N}^{{ - 1}}}$ является достаточно малой:

Это условие позволяет естественным образом перейти от использования дискретной переменной ${{x}_{j}}$ к непрерывной переменной $x \in [0,2\pi ]$. Кроме этого нас будет интересовать влияние изменения величины $N$ на асимптотику решений. Пусть количество элементов в (1) равно $N + c$, где $c$ – произвольно фиксированное целое значение. Положим $\mu = 2\pi {{(N + c)}^{{ - 1}}}$ и произведем нормировку времени $t \to {{M}^{{1/2}}}{{\varepsilon }^{{ - 1}}}t$. Тогда система (1) принимает вид

и выполнено условие периодичности

Уравнение (3) исследовалось многими авторами (см., например, [1–8]), причем основное внимание уделялось изучению так называемых регулярных решений. Напомним, что регулярные решения выделялись условием “хорошей” зависимости от параметра $\varepsilon $. Это такие решения, для которых справедливо асимптотическое представление

Для исследования регулярных решений с определенной степенью точности по параметру $\varepsilon $ от уравнения (3) осуществлялся переход к специальному нелинейному уравнению с частными производными. Основные результаты касались, в основном, вопросов о нахождении точных решений и о выявлении свойств интегрируемости полученных уравнений с частными производными.

Отметим еще, что в работе [8] получены интересные результаты о взаимодействии волн в таких уравнениях.

Для параметра $\mu $ имеем асимптотическую формулу

Через ${{E}_{ \pm }}(t,x,\varepsilon )$ обозначим функции

В настоящей работе изучаются нерегулярные решения краевой задачи (3), (4). Структура таких решений будет состоять из суперпозиции функций, гладко (регулярно) зависящих от параметра ε, и функций, гладко зависящих от параметра ε^–1. Остановимся на этом подробнее.

Прежде всего отметим, что любая тождественно постоянная функция 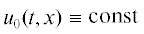является состоянием равновесия краевой задачи (3), (4). Будем исследовать локальное поведение решений в окрестности каждого такого состояния равновесия. Тем самым исследуются решения с достаточно малыми (и не зависящими от ε) отклонениями их $2\pi $-периодических и непрерывных по x начальных условий. При исследовании локального поведения решений важную роль играет линеаризованное на состояниях равновесия краевая задача

В свою очередь структура решений (5) определяется расположением корней характеристического уравнения

Рассмотрим асимптотику корней (6) для достаточно больших – порядка ${{\varepsilon }^{{ - 1}}}$ значений величин k.

Сначала фиксируем произвольно величину $\delta > 0$ и будем предполагать, что

Ниже через $\Theta = \Theta (\delta ,\varepsilon ) \in [0,1)$ будем обозначать величину, которая дополняет до целого выражения $\delta {{\varepsilon }^{{ - 1}}}$.

Пусть K_ε – совокупность таких целых чисел, которые заданы формальным соотношением

Обратим внимание, что в силу равенства ε = = $2\pi {{N}^{{ - 1}}}$ величина $2\pi n{{\varepsilon }^{{ - 1}}}$ является целым числом.

Будет рассмотрен вопрос о таких решениях краевой задачи (3), (4), в основе формирования которых присутствуют моды с номерами из K_ε. Для нахождения главных частей таких решений будут получены специальные системы уравнений в частных производных, представляющие собой системы из двух связанных нелинейных уравнений Шрёдингера.

Каждому элементу множества K_ε соответствует значение корня $\lambda _{{m,n}}^{ \pm }(\varepsilon )$ характеристического уравнения (6), а каждому корню $\lambda _{{m,n}}^{ \pm }(\varepsilon )$ отвечает решение линейной краевой задачи (5)

а значит эта же краевая задача имеет совокупность решений

Выражение (8) можно существенно упростить. Для этого введем обозначения. Положим

Тогда (8) преобразуется к виду

u(t, x, ε) = ${{u}^{ + }}(t,x,\varepsilon ) + {{u}^{ - }}(t,x,\varepsilon )$

и

где $\tau = \varepsilon t$,

${{\xi }_{ \pm }}(\tau ,{{x}_{ \pm }},{{y}_{ \pm }})$ = $\sum\limits_{m,n = - \infty }^\infty {{\xi }_{{m,n \pm }}}(\tau ){\text{exp}}(im{{x}_{ \pm }}$ + iny_±),

В следующем разделе сформулируем основной результат. Из него будет следовать, что нелинейная краевая задача (3), (4) имеет совокупность таких нерегулярных решений, главные члены асимптотики которых определяет выражение

Для нахождения неизвестных амплитуд ${{\xi }_{ \pm }}(\tau ,{{x}_{ \pm }},{{y}_{ \pm }})$ приведем специальную систему связанных нелинейных уравнений Шрёдингера. Через $\overline {cc} $ здесь и ниже обозначаются выражения, комплексно сопряженные к предыдущему слагаемому.

В разделе 2 отдельно рассмотрен случай, когда для некоторого целого k₀ выполнено равенство

Сразу отметим, что этот случай существенно отличается от случая (7).

В методическом плане обоснование приводимых ниже результатов опирается на работы [9–11].

1. ОСНОВНОЙ РЕЗУЛЬТАТ

Сначала введем несколько обозначений. Через $D,J$ и ${{J}_{0}}$ обозначим операторы, определенные на непрерывно дифференцируемых функциях ${v}(x,y)$ двух переменных $x$ и $y$ и действующих по правилам

Ниже потребуются следующие соотношения, которые вытекают из этих определений:

Через ${{W}_{2}}(\tau ,t,{{x}_{ \pm }},{{y}_{ \pm }},{{\varepsilon }^{{ - 1}}}(\delta + \varepsilon \Theta )x)$ обозначим функцию

где

Cформулируем основной результат. Рассмотрим две краевые задачи

в которых

Ниже через ${{\varepsilon }_{k}}({{\Theta }_{0}})\,(k = {{k}_{0}},{{k}_{0}} + 1, \ldots )$ обозначим такую последовательность, что ${{\varepsilon }_{k}}({{\Theta }_{0}}) \to 0$ при $k \to \infty $ и на которой величина $\Theta $ не меняется: $\Theta \left( {{{\varepsilon }_{k}}({{\Theta }_{0}})} \right) = {{\Theta }_{0}}$.

Положим

Теорема 1. Фиксируем произвольно положительное значение $\delta \ne \pi k$ $(k = 0,1,2, \ldots )$ и ${{\Theta }_{0}} \in [0,1)$. Пусть $\left( {{{\xi }_{ + }}(\tau ,x,y),{{\xi }_{ - }}(\tau ,x,y)} \right)$ – ограниченное при $\tau \to \infty $, $x \in [0,2\pi ]$, $y \in [0,2\pi ]$ вместе с производной по $\tau $ и первой и второй производным по $x$ и $y$ – решение краевых задач (14) при $\Theta = {{\Theta }_{0}}$. Тогда функция

при $\tau = {{\varepsilon }_{k}}({{\Theta }_{0}})t$, ${{x}_{ \pm }} = x \pm t\cos \left( {\frac{\delta }{2}} \right)$, ${{y}_{ \pm }}\, = \,y\, \mp \,ct{\text{cos}}\left( {\frac{\delta }{2}} \right)$, $y = 2\pi \varepsilon _{k}^{{ - 1}}({{\Theta }_{0}})x$ удовлетворяет краевой задаче (3), (4) с точностью до $O(\varepsilon _{k}^{3}({{\Theta }_{0}}))$.

В плане обсуждения этого результата отметим, что в обоих уравнениях (13) и (14) фигурируют одни и те же значения аргументов $\tau ,x,y$, а в формуле (15) аргументы функций ${{\xi }_{ \pm }}(\tau ,{{x}_{ \pm }},{{y}_{ \pm }})$ различные. Свести (13) и (14) к одинаковым аргументам удалось из-за того, что нелинейные выражения $(J{\text{|}}{{\xi }_{ \pm }}{{{\text{|}}}^{2}} - {{J}_{0}}{\text{|}}{{\xi }_{ \pm }}{{{\text{|}}}^{2}})$ зависят от аргумента $cx + y$. Это, в свою очередь, следует из равенств (9) и (11): $cx + y = c{{x}_{ + }} + {{y}_{ + }} = c{{x}_{ - }} + {{y}_{ - }}$.

2. РЕЗУЛЬТАТЫ ДЛЯ СЛУЧАЯ $\delta = 2\pi {{n}_{0}}$

Множество целых чисел ${{K}_{\varepsilon }}$ в этом случае имеет вид

Для корней $\lambda _{{m,n}}^{ \pm }(\varepsilon )$ характеристического уравнения (6) выполнены асимптотические равенства

Опираясь на структуру решений линеаризованной краевой задачи (5) с модами из ${{K}_{\varepsilon }}$, решения нелинейной краевой задачи (3), (4) ищем в виде

где $\tau = {{\varepsilon }^{2}}t$, ${{x}_{ \pm }} = x \pm t$, ${{y}_{ \pm }} = y \pm ct$.

Подставим (16) в (3) и будем приравнивать коэффициенты при одинаковых степенях $\varepsilon $. При ${{\varepsilon }^{1}}$ получаем верное равенство. На следующем шаге приходим к уравнению относительно ${{W}_{{20}}}$, ${{W}_{{2 \pm }}}$. Из него находим, что

а из условия разрешимости уравнений относительно ${{W}_{{2 \pm }}}$ приходим к соотношениям для ${{\xi }_{ \pm }}(\tau ,x,y)$:

Отсюда следует итоговое утверждение.

Теорема 2. Пусть краевая задача (17), (18) имеет ограниченное при $\tau \to \infty $, $x \in [0,2\pi ]$, $y\, \in \,[0,2\pi ]$ непрерывно дифференцируемое по $\tau $ и четырежды непрерывно дифференцируемое по $x$ и $y$ решение ${{\xi }_{ \pm }}(\tau ,x,y)$. Тогда функция

удовлетворяет краевой задаче (3), (4) с точностью до $O({{\varepsilon }^{3}})$.

Отметим, что уравнения (17) можно упростить. Для этого положим

В результате получим краевую задачу

Эту краевую задачу естественно назвать уравнением Кортевега–де-Фриза в двумерной пространственной области.

Функции ${{\xi }_{ \pm }}$ можно выразить через ${{\eta }_{ \pm }}$:

ВЫВОДЫ

Предложенный подход позволяет при построении асимптотики решений учитывать и более высокие по порядку $\varepsilon $ слагаемые. Кроме этого могут быть рассмотрены задачи с несколькими параметрами ${{\delta }_{1}}, \ldots ,{{\delta }_{j}}$; и, в том числе, при наличии среди них резонансных соотношений.

Обратим внимание, что в краевой задаче (14) присутствует “внутренний” параметр $\Theta $, который бесконечно много раз изменяется от $0$ до $1$ при $\varepsilon \to 0$. Это говорит о том, что при $\varepsilon \to 0$ может происходить неограниченный процесс прямых и обратных перестроек фазовых портретов. Некоторые иллюстрации этого явления приведены в работе [12].

Показано, что для описания главных приближений решений в различных областях фазового пространства краевой задачи (3) возникают различные уравнения в частных производных.

При $\delta \ne 2\pi n$ и $\delta = 2\pi {{n}_{0}}$ построены специальные нелинейные краевые задачи для нахождения медленно меняющихся амплитуд ${{\xi }_{ \pm }}(\tau ,{{x}_{ \pm }},{{y}_{ \pm }})$. Для каждого из этих двух случаев эти краевые задачи различны. В первом из них получены системы двух уравнений Шрёдингера, во втором – система двух уравнений Кортевега–де-Фриза. Асимптотические представления изученных выше нерегулярных решений содержат суперпозиции функций, зависящих от “медленного” времени $\tau = \varepsilon t$ (или $\tau = {{\varepsilon }^{2}}t$), от “среднего” времени $t$ и от “быстрого” времени ${{\varepsilon }^{{ - 1}}}t$. Кроме того, они содержат $2\pi $-периодичные компоненты по пространственным переменным $x$, $y = 2\pi {{\varepsilon }^{{ - 1}}}x$ и быстро осциллирующие по переменной ${{\varepsilon }^{{ - 1}}}x$.

Из приведенных выше формул следует, что при условии $\delta \ne 2\pi n$ влияние функций ${{\xi }_{ + }}$ и ${{\xi }_{ - }}$ друг на друга приводит только к изменению их фазовых составляющих. Если же $\delta = 2\pi {{n}_{0}}$, то это влияние проявляется существенно слабее [8] при учете слагаемых более высокого порядка малости в соответствующих краевых задачах. В этом можно проследить некоторые аналогии с выводами из [13, 14].

При $\delta \ne 2\pi n$ коэффициенты ${{\sigma }_{0}}$ и ${{\sigma }_{1}}$ в (14) зависят и от параметра $\alpha $ и от параметра $\beta $, а при $\delta = 2\pi {{n}_{0}}$ в (17), (18) фигурирует только параметр $\alpha $. Разными оказались и “порядки” “медленного” времени $\tau $. В первом случае $\tau = \varepsilon t$, а во втором – $\tau = {{\varepsilon }^{2}}t$, т.е. при $\delta = 2\pi {{n}_{0}}$ процессы протекают существенно медленнее. Отметим еще, что в обоих случаях амплитуда главных слагаемых решений имеет порядок $\varepsilon $.