Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 501, № 1, стр. 62-66

1. Для численного решения гиперболических систем законов сохранения [1] широко применяется схема CABARET [2], монотонность которой изучалась в [3–6]. Одно из преимуществ этой схемы заключается в том, что она локализует ударные волны точнее [7], чем схемы формально более высокого порядка, например, схема WENO5 [8]. Стандартный алгоритм схемы CABARET [2], аппроксимирующей гиперболическую систему дифференциальных уравнений, предполагает, что эта система допускает запись в форме инвариантов [1]. Для построения схемы CABARET, аппроксимирующей систему уравнений неизоэнтропической газовой динамики [1], не допускающей записи в форме инвариантов, используются квазиинварианты [2], определяемые неоднозначно.

В настоящей работе предлагается общий метод квазиинвариантов при построении схемы CABARET, аппроксимирующей гиперболическую систему законов сохранения, не допускающую запись в форме инвариантов. Применение этого метода вместе с дополнительной коррекцией потоков обеспечивает монотонизацию разностного решения при расчете разрывных решений с ударными волнами и контактными разрывами. В качестве примера рассмотрена система законов сохранения неизоэнтропической газовой динамики с политропным уравнением состояния [1]. Тестовые расчеты классической задачи Blast Wave [9] показали, что предлагаемая схема эффективно подавляет нефизические осцилляции, приводящие к неустойчивости разностного решения при расчете по другим вариантам схемы CABARET, в которых дополнительная коррекцией потоков отсутствует.

2. Рассмотрим строго гиперболическую систему законов сохранения

где ${\mathbf{u}}(x,t)$ – искомая, а ${\mathbf{f}}({\mathbf{u}})$ – заданная вектор-функции, содержащие m компонент. Строгая гиперболичность системы ((1)) означает, что все собственные значения ${{\lambda }_{i}}({\mathbf{u}})$ матрицы Якоби $A({\mathbf{u}}) = {{{\mathbf{f}}}_{{\mathbf{u}}}}({\mathbf{u}})$ действительны и различны, в силу чего соответствующие им левые собственные вектора ${{{\mathbf{l}}}^{i}}({\mathbf{u}})$ образуют базис в пространстве ${{\mathbb{R}}^{m}}$.

Известно [1], что при $m \geqslant 3$ дифференциальные формы ${{{\mathbf{l}}}^{i}}({\mathbf{u}})d{\mathbf{u}}$ могут быть неинтегрируемы и система ((1)) в этом случае не допускает полного набора инвариантов. Если некоторая дифференциальная форма ${{{\mathbf{l}}}^{i}}({\mathbf{u}})d{\mathbf{u}}$ интегрируема, то система (1) имеет инвариант ${{w}_{i}}({\mathbf{u}})$, сохраняющийся вдоль характеристик i-го семейства. Если дифференциальная форма ${{{\mathbf{l}}}^{i}}({\mathbf{u}})d{\mathbf{u}}$ неинтегрируема, то будем предполагать существование вектора ${{{\mathbf{\bar {u}}}}_{i}}[{\mathbf{u}}] = (\bar {u}_{1}^{i},...,\bar {u}_{s}^{i})$, где $s < m$, (состоящего из некоторых компонент вектора ${\mathbf{u}}$) такого, что интегрируемой является дифференциальная форма ${{{\mathbf{l}}}^{i}}({{{\mathbf{\bar {u}}}}_{i}}[{{{\mathbf{u}}}_{c}}],{{{\mathbf{\tilde {u}}}}_{i}}[{\mathbf{u}}])d{\mathbf{u}}$, где ${{{\mathbf{u}}}_{c}}$   – произвольный постоянный вектор, а ${{{\mathbf{\tilde {u}}}}_{i}}[{\mathbf{u}}] = (\tilde {u}_{1}^{i},...,\tilde {u}_{{m - s}}^{i})$ – вектор, состоящий из тех компонент вектора ${\mathbf{u}}$, которые не вошли в вектор ${{{\mathbf{\bar {u}}}}_{i}}[{\mathbf{u}}]$. Функцию ${{w}_{i}}({{{\mathbf{\bar {u}}}}_{i}}[{{{\mathbf{u}}}_{c}}],{\mathbf{u}})$, получаемую в результате такого интегрирования, будем называть квазиинвариантом системы (1). Инварианты системы (1) будем рассматривать как частный случай ее квазиинвариантов. В результате формируется вектор квазиинвариантов ${\mathbf{w}} = {\mathbf{W}}({\mathbf{u}})$, относительно которого будем предполагать, что преобразование ${\mathbf{W}}({\mathbf{u}})$ является невырожденным.

3. Схему CABARET, аппроксимирующую систему (1), будем строить на прямоугольной разностной сетке

в которой h – шаг сетки по пространству, а ${{\tau }_{n}}$ – шаг сетки по времени, определяемый из условия устойчивости

В этой схеме используются потоковые ${\mathbf{v}}_{j}^{n}\, = \,{\mathbf{v}}({{x}_{j}},{{t}_{n}})$ и консервативные ${\mathbf{v}}_{{j + 1/2}}^{n} = {\mathbf{v}}({{x}_{{j + 1/2}}},{{t}_{n}})$ переменные, заданные в целых x_j и полуцелых x_{j + 1/2} = = ${{x}_{j}} + h{\text{/}}2$ узлах разностной сетки.

Пусть ${\mathbf{v}}_{j}^{n}$, ${\mathbf{v}}_{{j + 1/2}}^{n}$ – известное численное решение на n-м временном слое ${{t}_{n}}$. Разностное решение ${\mathbf{v}}_{j}^{{n + 1}}$, ${\mathbf{v}}_{{j + 1/2}}^{{n + 1}}$ получается по схеме CABARET в четыре этапа. На первом этапе вычисляются величины

где ${{t}_{{n + 1/2}}} = {{t}_{n}} + {{\tau }_{n}}{\text{/}}2$ и ${{r}_{n}} = {{\tau }_{n}}{\text{/}}(2h)$. На втором этапе находятся предварительные значения ${\mathbf{\tilde {v}}}_{j}^{{n + 1}}$, которые используются на третьем этапе

На четвертом этапе определяются окончательные значения ${\mathbf{v}}_{j}^{{n + 1}}$. Алгоритм схемы на втором и четвертом этапах приводится ниже.

4. На втором этапе вычисляются квазиинварианты системы (1) в целых узлах $(n + 1)$-го временного слоя. Опишем процедуру этого вычисления для некоторого квазиинварианта ${{w}_{i}}$ (для краткости индекс i будем опускать). Сначала для каждой пространственной ячейки $[{{x}_{j}},{{x}_{{j + 1}}}]$ находятся значения

где ${\mathbf{b}} = {\mathbf{b}}_{{j + 1/2}}^{{n + 1/2}} = {\mathbf{\bar {v}}}[{\mathbf{v}}_{{j + 1/2}}^{{n + 1/2}}]$; при этом в каждом целом узле j определены два значения квазиинварианта $\left( {{{w}_{r}}} \right)_{j}^{n}$ и $\left( {{{w}_{l}}} \right)_{j}^{n}$, вычисляемые в ячейках, расположенных справа и слева от узла  j. При помощи значений (6) определяются величины

Следуя [2], величины (7) при помощи функции

корректируются по формулам в которых где $w_{{j + 1/2}}^{n} = w({\mathbf{b}},{\mathbf{v}}_{{j + 1/2}}^{n})$.

Значение квазиинварианта $\tilde {w}_{j}^{{n + 1}}$ определяется в зависимости от знаков скоростей характеристик

в ячейках, примыкающих к узлу j. Если $\lambda _{{j - 1/2}}^{{n + 1/2}} > 0$ и $\lambda _{{j + 1/2}}^{{n + 1/2}}\, \geqslant \,0$, то $\tilde {w}_{j}^{{n + 1}}\, = \,\left( {{{{\tilde {w}}}_{l}}} \right)_{j}^{{n + 1}}$; если $\lambda _{{j - 1/2}}^{{n + 1/2}}\, \leqslant \,0$ и $\lambda _{{j + 1/2}}^{{n + 1/2}}$ < 0, то $\tilde {w}_{j}^{{n + 1}} = \left( {{{{\tilde {w}}}_{r}}} \right)_{j}^{{n + 1}}$. Отдельно следует рассмотреть случаи, когда скорости характеристик (11) разных знаков. Если $\lambda _{{j - 1/2}}^{{n + 1/2}} \leqslant 0$ и $\lambda _{{j + 1/2}}^{{n + 1/2}} \geqslant 0$, то если $\lambda _{{j - 1/2}}^{{n + 1/2}} > 0$ и $\lambda _{{j + 1/2}}^{{n + 1/2}} < 0$, то выполняется экстраполяция

В завершении второй этапа по найденным значениям вектора квазиинвариантов $\widetilde {\mathbf{w}}_{j}^{{n + 1}}$ вычисляется вектор $\widetilde {\mathbf{v}}_{j}^{{n + 1}} = {{{\mathbf{W}}}^{{ - 1}}}(\widetilde {\mathbf{w}}_{j}^{{n + 1}})$, где W^–1 – преобразование, обратное к W.

5. По аналогии с [6] на четвертом этапе проводится дополнительная коррекция квазиинвариантов $\widetilde w_{j}^{{n + 1}}$. При выполнении неравенств $\lambda _{{j - 1/2}}^{{n + 1/2}} \leqslant 0$ и $\lambda _{{j + 1/2}}^{{n + 1/2}} \geqslant 0$ эта коррекция проводится по формуле

а в остальных случаях – по формуле в которой где $w_{{j \pm 1/2}}^{{n + 1}} = w({\mathbf{b}}_{{j \pm 1/2}}^{{n + 1/2}},{\mathbf{v}}_{{j \pm 1/2}}^{{n + 1}})$. После вычисления вектора ${\mathbf{w}}_{j}^{{n + 1}}$ определяются окончательные значения вектора ${\mathbf{v}}_{j}^{{n + 1}} = {{{\mathbf{W}}}^{{ - 1}}}({\mathbf{w}}_{j}^{{n + 1}})$.

Дополнительная коррекция потоков, аналогичная (14)–(16), является необходимым условием монотонности схемы CABARET при аппроксимации линейного гиперболического уравнения [3], квазилинейного закона сохранения [4, 5] и линейной гиперболической системы дифференциальных уравнений [6]. В различных вариантах схемы CABARET, рассматриваемых в [2], такая дополнительная коррекция потоков не применяется.

6. В качестве конкретной гиперболической системы (1) выберем систему уравнений неизэнтропической газовой динамики [1], для которой

с политропным уравнением состояния p = $(\gamma - 1)\rho \varepsilon $, где $\rho $, $u$, $\varepsilon $ и $p$ – плотность, скорость, внутренняя энергия и давление в газе, и $\gamma $ – показатель адиабаты. Характеристики этой системы распространяются со скоростями где $c = \sqrt {\gamma p{\text{/}}\rho } $ – скорость звука в газе.

Поскольку система (1), (17) имеет инвариант 

сохраняющийся вдоль характеристик второго семейства, то на поверхностях ${{w}_{2}} = {\text{const}}$ дифференциальные формы, соответствующие первому и третьему характеристическим уравнениям этой системы, интегрируемы [1]. Однако уравнения таких поверхностей можно получить только в результате решения системы (1), (17), в силу чего инварианты ${{w}_{1}}$ и ${{w}_{3}}$, сохраняющиеся вдоль характеристик первого и третьего семейств этой системы, в общем случае выписать в явном виде не удается. Поэтому в настоящей работе мы применяем для схемы CABARET (4)–(16) изохорические квазиинварианты [2]:

7. Рассмотрим для системы (1), (17) при $x \in [0,X]$ и $t \geqslant 0$, где X = 1, начально-краевую задачу Blast Wave [9] со следующими начальными

и граничными условиями, в которых X = 1. Численные расчеты данной задаче по схеме CABARET проводились на разностной сетке (2), в которой $j = 0,1,...,N$, где $N = X{\text{/}}h$ – количество пространственных узлов сетки. Начальные условия (18) с учетом обозначений (17) аппроксимировались по формулам а граничные условия непротекания ((19)) по формулам в которых $u_{j}^{n}$ – сеточная функция скорости газа. Поскольку в точном решении задачи (1), (17)–(19) давление газа может принимать достаточно малые значения, то для обеспечения положительности давления в разностном решении на каждом временном слое проводится следующая дополнительная корректировка численного значения давления: если давление в некотором узле разностной сетки меньше $\varepsilon = 0.0001$, то оно заменяется на значение $\varepsilon $.

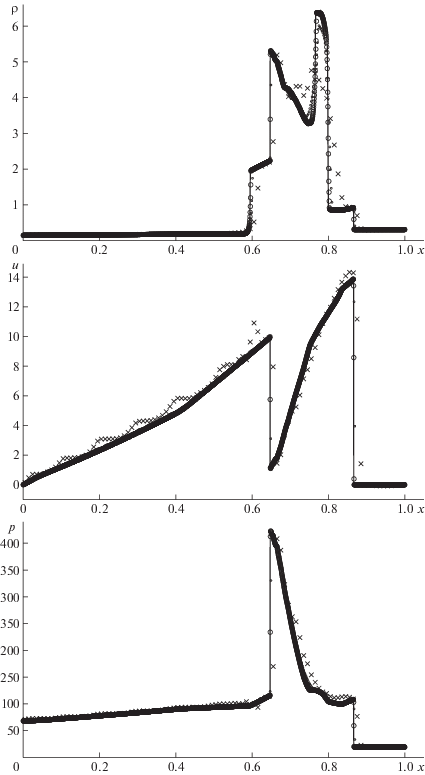
Тестовые расчеты задачи Blast Wave (17)–(19) показали, что в схеме CABARET [2], при построении которой применяются линейные квазиинварианты, а также в схеме CABARET (4)–(13) без дополнительной коррекции потоков (14)–(16), в начале численного расчета в окрестности левого контактного разрыва возникают нефизические осцилляции давления, которые с течением времени неограниченно возрастают, приводя к неустойчивости разностного решения. В схеме CABARET (4)–(16) эти нефизические осцилляции эффективно подавляются, что позволяет с достаточно высокой точностью рассчитывать задачу Blast Wave. Для иллюстрации процесса сходимости разностного решения к точному на рис. 1 и в табл. 1 в момент времени $t = 0.038$ приведены результаты расчета задачи (1), (17)–(19) по схеме CABARET (4)–(16) на последовательности сгущающихся сеток (2) с коэффициентом $z = 0.4$ в условии устойчивости (3). Точное решение, показанное на рис. 1 сплошной линией, моделируется численным расчетом по схеме PPM [9] на достаточно мелкой разностной сетке (2), (3). В табл. 1 приведены ошибки разностного решения, вычисляемые по формуле

где ${{N}_{h}} = X{\text{/}}h$ – количество пространственных узлов разностной сетки. Из таблицы следует, что в сеточной норме L₁ разностное решение сходится к точному решению приблизительно с первым порядком, что характерно для сильной сходимости в интегральных нормах разностных решений к точным решениям, содержащим ударные волны.

Предложенная модификация схемы CABARET обобщается на случай многомерных гиперболических систем законов сохранения, а также на случай уравнений газовой динамики с другими уравнениями состояния.