Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 502, № 1, стр. 42-45
Сравнительный анализ различных численно-статистических проекционных алгоритмов для решения задач теории переноса
Член-корреспондент РАН Г. А. Михайлов 1, 2, *, А. С. Корда 1, **, С. В. Рогазинский 1, 2, ***
1 Институт вычислительной математики и математической геофизики Сибирского отделения Российской академии наук
Новосибирск, Россия
2 Новосибирский государственный университет
Новосибирск, Россия
* E-mail: gam@sscc.ru
** E-mail: asc@osmf.sscc.ru
*** E-mail: svr@osmf.sscc.ru
Поступила в редакцию 29.10.2021
После доработки 29.10.2021
Принята к публикации 20.12.2021
- EDN: GDVOHS
- DOI: 10.31857/S2686954322010106
Аннотация
Проведен сравнительный анализ различных вариантов проекционного алгоритма метода Монте-Карло на примере оценки потока частиц через слой вещества с рассеянием типа Хеньи–Гринстейна. Исследована возможность минимизации среднего квадрата погрешности оценок путем уравнивания соответствующих стохастических и детерминированных слагаемых.
1. Проекционные статистические оценки. Рассматривается последовательность полиномов, ортонормированных с весом $p(x)$:
Известные (см., например, [1–3]) статистические проекционные оценки представим в виде
Здесь $\xi $ – случайная величина, которая в случае оценки плотности $\varphi $ моделируется согласно $\varphi $. Если же $\varphi $ – искомое решение интегрального уравнения 2-го рода, то $\xi $ – траектория моделируемой цепи Маркова “столкновений”, а $\{ {{\tilde {a}}_{i}}(\xi )\} $ – “оценки по столкновениям” специального вида (см. далее); N – объем выборки. Заметим, что детерминированный вариант разложения по полиномам Эрмита со значением $\alpha = 0.5$ представлен в [4].
Настоящая работа ориентирована в основном на решение интегральных уравнений $\varphi = K\varphi + f$ с субстохастическим ядром $k(x{\kern 1pt} ',x) \geqslant 0$, причем $\int k(x{\kern 1pt} ',x)dx \leqslant \rho < 1$, f – плотность распределения. В случае аналогового (прямого) моделирования [5] оценка по столкновениям имеет вид ξ = $\sum\limits_{k = 0}^{{{N}_{c}}} h({{x}_{k}})$, где $\{ {{x}_{k}}\} $ – обрывающаяся с вероятностью единица цепь Маркова с характеристиками $f(x),k(x{\kern 1pt} ',x)$ [5]. Известно следующее утверждение (см., например, [5]).
Лемма 1. Если $h \in {{L}_{\infty }}$, то в случае аналогового моделирования
Лемма 1 показывает, что использование проекционной оценки с $\alpha = 1$ для неограниченного интервала $X$ нецелесообразно.
На основе леммы 1 доказывается
Лемма 2. Если ${{p}^{{1 - \alpha }}}(x)|{{\Psi }_{i}}(x)|\,\, \leqslant {{C}_{{i,\alpha }}} < + \infty $, то в случае прямого моделирования
Оптимизация оценки $\tilde {\varphi }(z)$ (точнее, минимизация ее среднеквадратической погрешности, как в математической статистике) возможна в норме с весом ${{p}^{{1 - 2\alpha }}}(x)$, так как при этом по аналогии с [1] имеем
В случае бесконечного интервала X при существовании липшицируемой производной функции $\varphi $ в [3] для разложения по полиномам Эрмита получена оценка ${{\delta }_{2}}(m) \lesssim {{c}_{2}}{\text{/}}m$, которую, предположительно, можно перенести на полиномы Лагерра.
Несложно доказать следующее утверждение.
Лемма 3. Если
то(2)
${{m}_{{opt}}} = \sqrt {{{C}_{2}}{\text{/}}{{C}_{1}}} ,\quad {{\delta }_{k}}({{m}_{{opt}}}) = \sqrt {{{C}_{1}}{{C}_{2}}} ,\quad k = 1,2.$Следовательно, в случае приближенного выполнения равенств (1), определять ${{m}_{{opt}}}$ можно на основе уравнения ${{\delta }_{1}}(m) = {{\delta }_{2}}(m)$. При этом, согласно лемме 3, выполняются соотношения
Отметим, что рассматриваемые проекционные алгоритмы распространяются на оценки функциональных зависимостей в многомерных задачах, как, например, в рассматриваемой далее тестовой задаче для оценки осредненного решения.
2. Тестовая задача. В качестве тестовой рассматривалась задача об оценке плотности $\varphi (z)$ столкновений частицы в полубесконечном слое $z \geqslant 0$ рассеивающего и поглощающего вещества для источника столкновений с плотностью $f({{z}_{1}},{{z}_{2}},z;\omega ) = {{e}^{{ - z}}}\delta ({{z}_{1}} - 0)\delta ({{z}_{2}} - 0)\delta (\omega - {{\omega }_{0}}),$ $z > 0$, где ${{\omega }_{0}} = (0,0,1)$ – направление скорости частицы, вызывающей начальное столкновение.
Параметры среды: коэффициент ослабления $\sigma = 1$, вероятность рассеяния ${{\sigma }_{s}}{\text{/}}\sigma = 0.9$, вероятность поглощения ${{\sigma }_{c}}{\text{/}}\sigma = 0.1$, индикатриса рассеяния Хеньи–Гринстейна:
Средний косинус угла рассеяния ${{\mu }_{0}} = 0.9$.
Отметим, что при $\sigma \equiv 1$ осредненная по ${{z}_{1}},{{z}_{2}}$ плотность столкновений φ(z) = $\int \int \int \Phi ({{z}_{1}},{{z}_{2}},z;\omega )d{{z}_{1}}d{{z}_{2}}d\omega $, где $\Phi $ – интенсивность излучения. Таким образом, фактически рассматривается задача, близкая к проблеме Милна [6]. Для данных параметров довольно высокую точность имеет транспортное приближение [6], которое дает для $\varphi (z)$ следующую асимптотическую оценку:
Полагая $p(z) = {{\varphi }_{{as}}}(z)$, получаем соответствующую последовательность полиномов Лагерра [7]:
Было реализовано статистическое модели-рование [5] с целью оценки коэффициентов ${{a}_{i}},i = 1$, ..., 200, для вариантов с $\alpha = 0,\frac{1}{2},1$, т.е. для проекционных представлений вида:
Анализ результатов показал, что соотношение ${{\delta }_{2}}(m) \approx {{C}_{2}}{\text{/}}m$ здесь выполняется. Было реализовано 30 независимых оценок по $N = {{10}^{6}}$ траекториям. На их основе путем уравнивания ${{\delta }_{1}}(m)$ и ${{\delta }_{2}}(m)$ были получены приближенные значения ${{m}_{{opt}}}$ и $\delta ({{m}_{{opt}}})$. В табл. 1 эти результаты обозначены через eq.
Таблица 1.
Результаты расчетов для тестовой задачи
| Тип оценки | $\alpha = 0$ | $\alpha = 0.5$ | $\alpha = 1$ | ||||
|---|---|---|---|---|---|---|---|
| ${{m}_{{opt}}}$ | $\delta ({{m}_{{opt}}})$ | ${{m}_{{opt}}}$ | $\delta ({{m}_{{opt}}})$ | ${{m}_{{opt}}}$ | $\delta ({{m}_{{opt}}})$ | ||
| average | 46 | 1.6 × 10–5 | 35 | 3.2 × 10–5 | 16 | 2.9 × 10–4 | |
| eq | min | 19 | 1.2 × 10–5 | 13 | 2.4 × 10–5 | 7 | 1.9 × 10–4 |
| max | 114 | 2.3 × 10–5 | 67 | 4 × 10–5 | 32 | 5.9 × 10–4 | |
| average | 45 | 1.8 × 10–5 | 36 | 3 × 10–5 | 17 | 2.7 × 10–4 | |
| Л3 | min | 22 | 8.5 × 10–6 | 19 | 1.6 × 10–5 | 11 | 1.7 × 10–4 |
| max | 72 | 2.9 × 10–5 | 59 | 5 × 10–5 | 21 | 5.7 × 10–4 | |
Были также получены оценки ${{m}_{{opt}}}$ и $\delta ({{m}_{{opt}}})$ по формулам (2), с помощью осреднения коэффициентов: ${{C}_{1}}$ в интервале $0 \leqslant m \leqslant 20$, ${{C}_{2}}$ в интервале $10 \leqslant m \leqslant 20$ для α = 1 и ${{C}_{1}}$ в интервале $0 \leqslant m \leqslant 40$, ${{C}_{2}}$ в интервале $20 \leqslant m \leqslant 40$ для $\alpha = 0,0.5$. В табл. 1 эти значения обозначены через Л3.
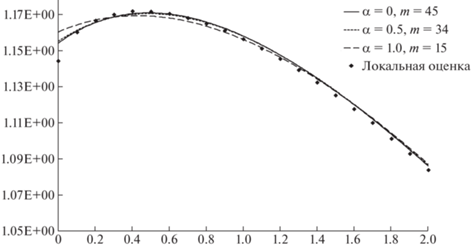
Сравнение оценок (1), (2), (3) в интервале $0 \leqslant z \leqslant 2$ дано графически на рис. 1. На этом же рисунке приведены значения локальной оценки $\varphi (z)$ (в точках ${{z}_{k}} = 0,0.1,0.2,...,10$), которые были получены подсчетом числа пересечений частицами соответствующих плоскостей с весом $1{\text{/|}}{{\omega }_{z}}{\text{|}}$ [5] для ${\text{|}}{{\omega }_{z}}{\text{|}} > 0.001$. При этом дисперсия оценки конечная, а относительное смещение не превосходит 0.1%, как и среднестатистическое уклонение в результате моделирования ${{10}^{8}}$ траекторий.
Кроме того, были вычислены ${{L}_{2}}$-нормы разности локальной и проекционных оценок для интервала $0 < z < 10$:
1) $0.00535$, 2) $0.00539$, 3) $0.00752$.
Эти оценки и графики, с учетом леммы 2 показывают предпочтительность здесь проекционной оценки с $\alpha = 0.5$, так как дополнительные расчеты показали, что она несколько более устойчива по отношению к выбору базовой плотности $p(z)$, сравнительно с вариантом $\alpha = 0$ и особенно с вариантом α = 1. Практически может быть так же важно, что эта оценка допускает оптимизацию в стандартной ${{L}_{2}}$-метрике.
Таблица 2 показывает влияние выбора плотности $p(z)$ на оценку с $\alpha = 0.5$. Здесь $\delta ({{m}_{{opt}}})$ минимизируется при $\lambda \approx 1{\text{/}}3.8$, в связи с тем, что плотность $\varphi (z)$ убывает существенно сильнее, чем ${{\varphi }_{{as}}}(z)$ в нижней части слоя.
Таблица 2.
Результаты расчетов по формулам (2) для $p(z) = {{e}^{{ - \lambda z}}}$ при $\alpha = 0.5$
| ${{\lambda }^{{ - 1}}}$ | 7.1 | 6.3 | 5.4 | 4.6 | 3.8 | 3 | 2.2 | 1.6 |
| ${{m}_{{opt}}}$ | 42 | 39 | 36 | 34 | 32 | 31 | 30 | 31 |
| $\delta ({{m}_{{opt}}})$ | 3.25 × 10–5 | 3.14 × 10–5 | 3.04 × 10–5 | 3.01 × 10–5 | 3.01 × 10–5 | 3.13 × 10–5 | 3.33 × 10–5 | 3.68 × 10–5 |
Отметим, что представленные в табл. 1, 2 соотношения результатов для разных значений параметров $\alpha $ и $\lambda $ получены на одном и том же ансамбле траекторий, что существенно повышает их статистическую значимость.
3. Дополнительная задача для конечного слоя. Решалась также задача о переносе частиц через конечный слой $0 \leqslant z \leqslant H = 10$ для вещества с радиационными параметрами из раздела 2.
Для корректного использования разложения соответствующей плотности $\varphi (z) = {{\varphi }_{H}}(z)$ по полиномам Лагерра процесс переноса моделировался как и в разделе 2 в полубесконечном слое, но столкновения в точках с координатой $z \leqslant H$ не учитывались на траекториях, вышедших (до их реализации) из рассматриваемого конечного слоя. При этом получалась несмещенная оценка плотности ${{\varphi }_{H}}(z)$ для слоя и, как показали расчеты, приблизительно выполнялось соотношение ${{\delta }_{2}}(m) \approx {{C}_{2}}{\text{/}}m$. В результате проведенных расчетов получены результаты, аналогичные результатам, приведенным в разделе 2; при этом для $\alpha = 0.5$ существенная дополнительная погрешность (с превышением от 1 до 10%) получается лишь при $z > 9$; соответствующее ${{L}_{2}}$-уклонение равно 0.02. Это показывает, что разработанная методика оптимизации может быть подходящей и для оценки плотности ${{\varphi }_{H}}(z)$ с указанной выше искусственной модификацией моделирования траекторий, которую можно рассматривать как регуляризацию стохастической проекционной оценки.
Список литературы
Ченцов Н.Н. Статистические решающие правила и оптимальные выводы. М.: Наука, 1972.
Mikhailov G.A., Tracheva N.V., Ukhinov S.A. Randomized projection method for estimating angular distributions of polarized radiation based on numerical statistical modeling // Comput. Math. and Math. Phys. 2016. V. 56. № 9. P. 1540–1550. https://doi.org/10.7868/S0044466916090155
Rogasinsky S.V. Two variants of Monte Carlo projection method for numerical solution of nonlinear Boltzmann equation // Russian Journal of Numerical Analysis and Mathematical Modelling. 2019. V. 34 (3). P. 143–150. https://doi.org/10.1515/rnam-2019-0012
Grad H. On the kinetic theory of rarefied gases // Comm. Pure and Appl. Math. 1949. V. 2. P. 331–407.
Марчук Г.И., Михайлов Г.А., Назаралиев М.А. и др. Метод Монте-Карло в атмосферной оптике. Новосибирск: Наука, 1976.
Davison B. Neutron Transport Theory. Oxford University Press, 1957.
Jackson D. Fourier Series And Orthogonal Polynomials. The University of Minnesota, 1941.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления