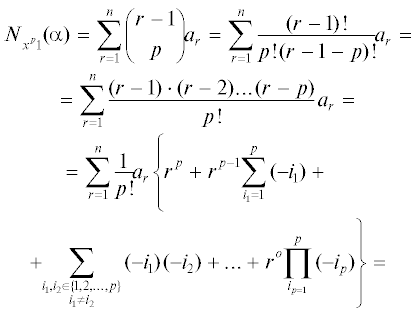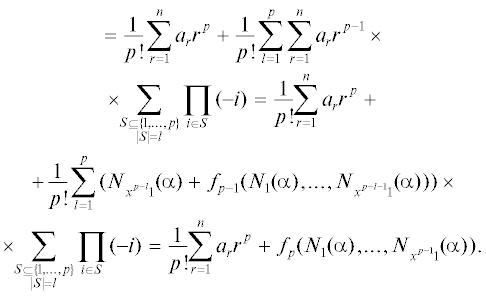Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 503, № 1, стр. 16-22

1. ПОСТАНОВКА ЗАДАЧИ

Введем следующие обозначения и определения. Греческими буквами будем обозначать слова, малыми латинскими – символы алфавита. Пусть $E_{2}^{n}$ – множество слов длины $n$ из алфавита {0, 1}. Для слова $\alpha = \left( {{{a}_{1}}{{a}_{2}} \ldots {{a}_{n}}} \right) \in E_{2}^{n}$ символом $\left| \alpha \right|$ обозначается сумма его элементов: $\left| \alpha \right| = {{a}_{1}} + {{a}_{2}}$ + + ... + a_n. Пусть λ означает пустое слово, т.е. слово, длина которого равна нулю. Возведение слова α в степень s является краткой записью для слова, состоящего из $s$ повторов слова α, т.е. α^s = = ${{\beta }_{1}}{{\beta }_{2}} \ldots {{\beta }_{s}}$, где ${{\beta }_{i}} = \alpha ,i \in \left\{ {1,~2,~ \ldots ,s} \right\}$.

Для заданного слова $\alpha = \left( {{{a}_{1}}{{a}_{2}} \ldots {{a}_{n}}} \right) \in E_{2}^{n}$ и заданного опорного вектора ${v} = \left( {{{{v}}_{1}}{{{v}}_{2}} \ldots {{{v}}_{n}}} \right)$, где ${{{v}}_{i}} \in \{ 0,~1\} $, $~i \in \{ 1,~2, \ldots ,~n\} $ операция фрагментирования $\langle \alpha \cdot {v}\rangle $ строит слово длины $\left| {v} \right|$ по следующему правилу:

Фрагментом, или подсловом, слова α = = $({{a}_{1}}{{a}_{2}} \ldots {{a}_{n}})\, \in \,E_{2}^{n}$ будем называть слово $\tilde {\alpha } \in E_{2}^{n}$ следующего вида:

Пусть $f{\text{*}}\left( \alpha \right)$ – это наименьшая длина фрагментов k, при которой гарантирована однозначность восстановления слова α длины n по мультимножеству его подслов длины k.

Задача. В общем виде задача о восстановлении слова по мультимножеству подслов формулируется следующим образом. Заданы:

набор опорных векторов $V = \{ {{{v}}^{1}},~{{{v}}^{2}},~ \ldots ,~{{{v}}^{N}}\} $, ${{{v}}^{i}} \in E_{2}^{n},{\text{|}}{{{v}}^{i}}{\text{|}} = k,i \in \{ 1,~2,~ \ldots ,~N\} $,

и множество слов $X = \{ {{\chi }^{1}},~{{\chi }^{2}},~ \ldots ,~{{\chi }^{N}}\} $, ${{\chi }^{i}} \in E_{2}^{k}$, $i \in \{ 1,~2, \ldots ,~N\} $.

Требуется проверить, является ли набор векторов X набором фрагментов фиксированной длины некоторого неизвестного слова $\alpha \in E_{2}^{n}$, построенных с помощью операции фрагментирования векторами из V, и найти все возможные решения.

При этом все оценки, получаемые для случая двоичного алфавита, остаются верными и для произвольного алфавита [3], так как в случае алфавита $\left\{ {0,1, \ldots ,~k} \right\}$ задача сводится к набору из k задач в двоичном алфавите с помощью отображений:

Поэтому далее будут рассмотрены только двоичные слова $\alpha = \left( {{{a}_{1}}{{a}_{2}} \ldots {{a}_{n}}} \right),~{{a}_{i}} \in \left\{ {0,~1} \right\}$. Более того, нас будут интересовать периодические слова.

Слово $\alpha = \left( {{{a}_{1}}{{a}_{2}} \ldots {{a}_{n}}} \right),~{{a}_{i}} \in \left\{ {0,~1} \right\}$ называется периодическим с периодом p, если

При этом подслово $\tilde {\alpha } = {{a}_{1}}{{a}_{2}} \ldots {{a}_{p}}$ будем называть порождающим подсловом для слова α вида (1).

2. СОСТОЯНИЕ ЗАДАЧИ

Для задачи о восстановлении слова по подсловам известно ее сведение к проверке единственности решения диофантовых уравнений определенного вида [2]. Показано, что задача о существовании и единственности решения является NP-полной.

В случае полного мультимножества фрагментов ($V = E_{2}^{n}$) установлено [14], что для однозначного восстановления слова $\alpha $ длины $n$ необходима длина $k \geqslant {\text{exp}}\left( {\Omega \left( {\log n} \right)} \right)$.

Для того же случая полного мультимножества фрагментов известны следующие оценки на достаточную длину [3, 13, 12 ]: $k\,\, \geqslant \,\,\left\lfloor {\frac{n}{2}} \right\rfloor $, $k\,\, \geqslant \,\,(1\,\, + \,\,o(1))\sqrt {n{\text{log}}n} $, $k \geqslant \left\lfloor {\frac{{16}}{7}\sqrt n } \right\rfloor + 5$.

Было изучено несколько частных случаев. Так, показано [15], что для слов, состоящих из l серий, достаточно фрагментов длины l.

3. РЕЗУЛЬТАТЫ

Сформулируем первую теорему.

Теорема 1. Для однозначного восстановления периодического слова длины n с периодом p по мультимножеству всех его фрагментов длины k достаточно выполнения условия

Перед доказательством введем следующее

Определение 1. Пусть ${{N}_{\beta }}\left( \alpha \right)$ – это число фрагментов, равных β, в слове α.

В [2] показано, что по ${{N}_{\beta }}\left( \alpha \right)$ для всех двоичных слов β длины k однозначно восстанавливаются числа фрагментов всех длин меньше k. Далее сформулируем и докажем лемму, которая непосредственно следует из системы уравнений в [2].

Лемма 1. Для любого слова α по набору его фрагментов вида ${{x}^{j}}1$ однозначно определяется набор его моментов вида $\mathop \sum \limits_{r = 1}^n {{a}_{r}}{{r}^{j}}$.

Доказательство. Получим формулы для ${{N}_{{{{x}^{j}}1}}}\left( \alpha \right)$ при разных j:

Функции ${{f}_{2}},~{{f}_{3}},~ \ldots ,~{{f}_{{k - 1}}}$ вычисляются на основе комбинаторных соотношений. Например, найдем выражение функции ${{f}_{p}}({{N}_{1}}(\alpha ),~ \ldots ,{{N}_{{{{x}^{{p - 1}}}1}}}(\alpha ))$, $~2 \leqslant p \leqslant k - 1$, через полученные на предыдущих шагах ${{f}_{1}},~ \ldots ,~{{f}_{{p - 1}}}$ (при этом можно положить ${{f}_{0}} \equiv 0$):

Так как, по предположению, все ${{f}_{1}},~ \ldots ,~{{f}_{{p - 1}}}$ известны, то известна и ${{f}_{p}}\left( {{{N}_{1}}\left( \alpha \right),~ \ldots ,{{N}_{{{{x}^{{p - 1}}}1}}}\left( \alpha \right)} \right)$.

Теперь мы можем перейти к доказательству теоремы 1.

Доказательство. Итак, доказательство базируется на результатах, полученных в [13] для достаточной для однозначной реконструкции слова длины фрагментов в случае произвольных слов. Оценка величины f*(α) в [13] получена на основе анализа следующей системы уравнений:

для которой при $f{\text{*}}\left( \alpha \right) \leqslant \left( {1 + o\left( 1 \right)} \right)\sqrt {n~{\text{log}}~n} $ решение единственно.

Пусть слово α состоит из $l = \frac{n}{p}$ периодов: $\alpha = {{({{a}_{1}}{{a}_{2}} \ldots {{a}_{p}})}^{l}}$. Тогда нулевое уравнение $\mathop \sum \limits_{r = 1}^n {{a}_{r}}$ = = s₀(α) можно переписать в виде $\mathop \sum \limits_{r = 1}^p {{a}_{r}} = \frac{{{{s}_{0}}\left( \alpha \right)}}{l}$. И для произвольного индекса $k'$ от 1 до k – 1 включительно:

где ${{f}_{{k'}}}$ – линейная функция, и далее доказательство теоремы в точности повторяет доказательство из [13].

Сформулируем более сильное утверждение.

Теорема 2. Для однозначного восстановления периодического слова длины n с периодом p по мультимножеству всех его фрагментов длины k достаточно выполнения условия

Доказательство. Доказательство основано на [12], где авторы доказывают возможность однозначной реконструкции слова по его подсловам не из анализа системы уравнений (2), как было проделано в [13], но из анализа похожей системы следующего вида:

выписанной для двух слов $\alpha = {{a}_{1}} \ldots {{a}_{n}}$ и $\beta = {{b}_{1}} \ldots {{b}_{n}}$. Доказывается, что слова α и ${{\beta }}$ имеют одинаковые мультимножества подслов длины k тогда и только тогда, когда система (3) имеет нетривиальное решение $\left( {{{a}_{1}}, \ldots ,{{a}_{n}},{{b}_{1}}, \ldots ,{{b}_{n}}} \right)$. Таким образом, доказательство сводится к поиску условия, при котором система диофантовых уравнений (3) имеет только тривиальное решение. Авторы [12] затем ссылаются на [16], где получен следующий результат:

Для случая же периодических слов ранее в данной работе при доказательстве теоремы 1 показано, как систему (3) можно переписать в переменных только ${{a}_{1}}, \ldots ,{{a}_{p}},{{b}_{1}}, \ldots ,{{b}_{p}}$, где p – период слова. Таким образом, оценка на достаточную для однозначного восстановления исходного слова длину подслов получается равной

Реконструкция слова остается возможной и тогда, когда само слово непериодическое, но состоит из нескольких подслов, по крайней мере одно из которых периодическое. Далее мы рассмотрим несколько случаев таких слов. Каждый случай будет оформлен в виде отдельной теоремы, доказательство которой будет опираться на уже доказанное ранее для периодического слова (теорема 2).

Теорема 3. Пусть слово $\alpha $ состоит из двух подслов: префикса и суффикса. Причем оба подслова периодические:

Тогда при $l \geqslant m{{q}^{{\left\lfloor {\frac{{16}}{7}\sqrt P } \right\rfloor + 5}}}$, где $P \equiv {\text{max}}\left( {p,q} \right)$, для однозначного восстановления слова (4) достаточно длины фрагментов $k \geqslant \left\lfloor {\frac{{16}}{7}\sqrt P } \right\rfloor + 5$.

Доказательство. Найдем ${{s}_{0}}\left( \alpha \right)$:

При $mq < l$ получаем $\frac{{m\left( {{{a}_{1}} + \ldots + {{a}_{q}}} \right)}}{l} < 1$, поэтому

Рассмотрим случай ${{s}_{1}}\left( \alpha \right)$:

Распишем первую сумму в выражении для ${{s}_{1}}\left( \alpha \right)$ (5):

Аналогично для второй суммы из выражения (5) получаем:

И в итоге имеем:

При условии $mq(q + 1){\text{/}}2 < l$ уравнения для префикса и суффикса разделяются, как и в случае с ${{s}_{0}}\left( \alpha \right)$. Перейдем теперь к случаю произвольного $k'$, такого что $2 \leqslant k' \leqslant k - 1$:

Распишем первую сумму:

В последнем переходе мы оставили отдельно член с показателем степени при r, равном $k'$ (при $j = k'$). Члены, куда r входит в меньшей степени, мы представили с помощью линейной функции ${{g}_{{k'}}}$.

Аналогично для второй суммы имеем:

Где снова в последнем переходе мы оставили отдельно член с показателем степени при r, равном $k'$ (при $j = k'$ и s = 0). Члены, куда r входит в меньшей степени, мы представили с помощью линейной функции ${{h}_{{k'}}}$.

Таким образом, объединяя результаты, полученные для обеих сумм, мы можем вернуться к вычислению ${{s}_{{k'}}}\left( \alpha \right)$:

где за ${{f}_{{k'}}}$ мы обозначили линейную функцию от ${{s}_{{k' - 1}}}, \ldots ,{{s}_{0}}$, являющуюся суммой функций ${{g}_{{k'}}}$ и ${{h}_{{k'}}}$.

Так как $\mathop \sum \limits_{k = 1}^n {{k}^{p}} \to \frac{{{{n}^{{p + 1}}}}}{{p + 1}}$, то при $m \cdot \frac{{{{q}^{k}}}}{k} < l$ разделяются все уравнения и получается две системы. Поэтому, по доказанному ранее для случая периодического слова (теорема 2), при $l \geqslant m{{q}^{{\left\lfloor {\frac{{16}}{7}\sqrt P } \right\rfloor + 5}}}$, где $P \equiv {\text{max}}\left( {p,q} \right)$, размер подслов ограничивается следующим образом: $k \geqslant \left\lfloor {\frac{{16}}{7}\sqrt P } \right\rfloor + 5$.

Следствие 1. При m = 1 слово $\alpha $ имеет вид слова с непериодическим префиксом и периодическим суффиксом:

При длине суффикса, большей длины префикса: $l \geqslant {{q}^{{\left\lfloor {\frac{{16}}{7}\sqrt P } \right\rfloor + 5}}}$ – для однозначного восстановления слова $\alpha $ достаточно подслов длины $k \geqslant \left\lfloor {\frac{{16}}{7}\sqrt P } \right\rfloor + 5$ при $P \equiv {\text{max}}\left( {p,q} \right)$.

Теорема 4. Пусть слово α состоит из трех подслов: периодического префикса $\bar {\alpha }$, периодического суффикса $\hat {\alpha }$ и непериодического корня $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\alpha } $:

Тогда при $m \geqslant {{s}^{{{{k}^{ \star }}}}}$ и $l \geqslant \left( {m - 1} \right){{q}^{{{{k}^{ \star }}}}} + {{(q + s)}^{{{{k}^{ \star }}}}}$, где ${{k}^{ \star }} = \left\lfloor {\frac{{16}}{7}\sqrt P } \right\rfloor + 5$ и $P \equiv {\text{max}}\left( {p,q,s} \right)$, для однозначного восстановления слова (6) достаточно $k \geqslant {{k}^{ \star }}$.

Доказательство. Доказательство опирается на теоремы 2 и 3.

Рассмотрим ${{s}_{0}}\left( \alpha \right)$:

Тогда при $mq + s < l$ разделяются уравнения для двух подслов: $\bar {\alpha }~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\alpha } $ и $\hat {\alpha }$.

Рассмотрим $k'$, такой что $1 \leqslant k' \leqslant k - 1$. Опуская подробные выкладки, аналогичные уже приведенным в доказательстве теоремы 3, получаем:

где ${{f}_{{k'}}}$ – линейная функция. Таким образом, при выполнении условия $l \geqslant m{{q}^{{k_{1}^{ \star }}}} + {{(q + s)}^{{k_{1}^{ \star }}}} - {{q}^{{k_{1}^{ \star }}}}$, где $k_{1}^{ \star } = \left\lfloor {\frac{{16}}{7}\sqrt {{{P}_{1}}} } \right\rfloor + 5$ и ${{P}_{1}} = {\text{max}}\left( {p,qm + s} \right)$, мы получаем разделимость уравнений для слов $\bar {\alpha }~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\alpha } $ и $\hat {\alpha }$, а потому и восстановимость целого слова при ограничении на длины подслов $k \geqslant k_{1}^{ \star }$.

Однако мы также можем отдельно рассмотреть вопрос о восстановимости слова $\bar {\alpha }~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\alpha } $. Действительно, по следствию 1, получаем, что для реконструкции слова $\bar {\alpha }~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\alpha } $ по множеству его подслов достаточно, чтобы $m \geqslant {{s}^{{k_{2}^{ \star }}}}$, где $k_{2}^{ \star } = \left\lfloor {\frac{{16}}{7}\sqrt {{{P}_{2}}} } \right\rfloor + 5$, P₂ = = ${\text{max}}(q,s)$. Тогда длина подслов ограничивается как $k \geqslant k_{2}^{ \star }$.

Объединяя условия с $k_{1}^{ \star }$ и $k_{2}^{ \star }$, получаем, что слово α восстановимо по подсловам при $m \geqslant {{s}^{{{{k}^{ \star }}}}}$, $l \geqslant \left( {m - 1} \right){{q}^{{{{k}^{ \star }}}}} + {{(q + s)}^{{{{k}^{ \star }}}}}$, где ${{k}^{ \star }} = \left\lfloor {\frac{{16}}{7}\sqrt P } \right\rfloor + 5$ и $P \equiv {\text{max}}\left( {p,q,s} \right)$. Длина подслов при этом $k \geqslant {{k}^{ \star }}$.

Замечание. Длина корня s = 0 дает случай, уже рассмотренный в теореме 3.

Следствие 2. Длина корня s = 1 равносильна наличию одного символа между двумя периодическими подсловами в слове α. В таком случае $\alpha $ восстановимо по подсловам при $l \geqslant (m - 1){{q}^{{{{k}^{ \star }}}}} + {{(q + 1)}^{{{{k}^{ \star }}}}}$, где ${{k}^{ \star }} = \left\lfloor {\frac{{16}}{7}\sqrt P } \right\rfloor + 5$ и $P \equiv {\text{max}}\left( {p,q} \right)$. Длина подслов k ограничивается соотношением: $k \geqslant {{k}^{ \star }}$.

Следствие 3. Пусть в слове α вида (6) порождающие подслова у префикса и суффикса одинаковы:

Пусть ${{k}^{ \star }} = \left\lfloor {\frac{{16}}{7}\sqrt P } \right\rfloor + 5$ и $P \equiv {\text{max}}\left( {q,s} \right)$. Тогда при $l + m \geqslant {{s}^{{{{k}^{ \star }}}}}$ слово $\alpha $ однозначно восстановимо при $k \geqslant {{k}^{ \star }}$.

Доказательство. Уравнение (7) в случае слова α указанной структуры примет вид:

А потому при $m + l \geqslant {{(q + s)}^{{{{k}^{ \star }}}}} - {{q}^{{{{k}^{ \star }}}}}$ получаем разделимость уравнений для порождающего подслова префикса (суффикса) и для корня.

Теорема 5. Пусть слово α имеет вид

т.е. образовано повторением подслова, которое, в свою очередь, состоит из периодического префикса и суффикса. Тогда при $l \geqslant m{{q}^{{{{k}^{ \star }}}}}$, где ${{k}^{ \star }}\, = \,\left\lfloor {\frac{{16}}{7}\sqrt P } \right\rfloor $ + 5 и $P \equiv {\text{max}}\left( {p,q} \right)$, для однозначного восстановления слова (8) достаточно $k \geqslant {{k}^{ \star }}$.

Доказательство. Начнем с вычисления ${{s}_{0}}(\alpha )$:

При $m < l$ получаем разделимость уравнений:

Введя обозначение $\tilde {n} \equiv qm + pl$, выразим теперь ${{s}_{{k'}}}\left( \alpha \right)$ при $k'$, таком что $1 \leqslant k' \leqslant k - 1$:

Таким образом, при $\frac{m}{l} \cdot \frac{{{{q}^{k}}}}{k} < 1$ все уравнения разделяются и получается две системы. По доказанной ранее для периодического слова теореме 2, при $l \geqslant m{{q}^{{{{k}^{ \star }}}}}$, где ${{k}^{ \star }} = \left\lfloor {\frac{{16}}{7}\sqrt P } \right\rfloor + 5$ и $P \equiv {\text{max}}\left( {p,q} \right)$, слово α восстановимо при $k \geqslant {{k}^{ \star }}$.

Замечание. Если N = 1, то получаем результат, доказанный ранее в теореме 3 для слова, состоящего фактически из одного повтора подслова с периодическими суффиксом и префиксом.

4. ЗАКЛЮЧЕНИЕ

В работе получена оценка на длину подслова k, достаточную для однозначного восстановления периодического слова длины n с периодом p по мультимножеству его подслов фиксированной длины: $k \geqslant \left\lfloor {\frac{{16}}{7}\sqrt p } \right\rfloor + 5$. Также получены оценки на k для следующих слов, не являющихся периодическими, но содержащими периодические подслова. Так, для слов, состоящих из периодического префикса и периодического суффикса, доказана возможность однозначного восстановления при достаточной длине суффикса. Показано, что слова, состоящие из периодического префикса, периодического суффикса и непериодического корня, могут быть однозначно восстановлены по мультимножеству фрагментов длины k при выполнении двух условий: малом по сравнению с префиксом корне, с одной стороны, и малом по сравнению с суффиксом префиксе, с другой. Доказана оценка для k в случае периодического слова, порожденного подсловом, в свою очередь, состоящим из двух частей: периодического суффикса и префикса.