Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 503, № 1, стр. 5-10

1. Пусть X – неприводимое алгебраическое многообразие над алгебраически замкнутым полем $\mathbb{K}$ нулевой характеристики, снабженное действием связной редуктивной алгебраической группы G. Всякое нетривиальное регулярное действие на X аддитивной группы ${{\mathbb{G}}_{a}} = (\mathbb{K}, + )$ индуцирует алгебраическую подгруппу в группе автоморфизмов ${\text{Aut}}(X)$, называемую ${{\mathbb{G}}_{a}}$-подгруппой. Для произвольной ${{\mathbb{G}}_{a}}$-подгруппы $H$ на X всякий ненулевой элемент одномерной алгебры Ли ${\text{Lie}}(H)$ естественным образом задает локально нильпотентное дифференцирование (кратко ЛНД) $\partial $ на алгебре регулярных функций $\mathbb{K}[X]$, причем в случае квазиаффинного X подгруппа H может быть восстановлена при помощи взятия экспоненты от $\partial $.

В настоящей работе нас будут интересовать ${{\mathbb{G}}_{a}}$‑подгруппы на X, нормализуемые действием борелевской подгруппы $B \subset G$. Следуя работе [1], мы называем такие ${{\mathbb{G}}_{a}}$-подгруппы $B$-корневыми подгруппами на X. Для всякой $B$-корневой подгруппы H на $X$ присоединенное действие группы $B$ на ${\text{Lie}}(H)$ сводится к умножению на характер группы $B$, который мы обозначим через ${{\chi }_{H}}$ и будем называть весом H. Если $\partial $ – локально нильпотентное дифференцирование на $\mathbb{K}[X]$, соответствующее H, то $\partial $ также нормализуется группой $B$, причем с тем же весом ${{\chi }_{H}}$.

2. Всюду далее будем предполагать, что многообразие X является сферическим, т.е. оно нормально и обладает открытой $B$-орбитой. Обозначим через ${{\mathcal{D}}^{B}}$ (соответственно ${{\mathcal{D}}^{G}}$) конечное множество всех $B$-инвариантных (соответственно $G$‑инвариантных) простых дивизоров в X. Элементы множества $\mathcal{D} = {{\mathcal{D}}^{B}}{{\backslash }}{{\mathcal{D}}^{G}}$ традиционно называются красками сферического многообразия X.

Напомним известное разделение красок в X на три типа (см. [2, 3]). Зафиксируем произвольную краску $D \in \mathcal{D}$. Для нее в группе $G$ всегда можно выбрать минимальную параболическую подгруппу $Q \supset B$ с условием $QD \ne D$. Для каждой подгруппы $F \subset Q$ обозначим через $\bar {F}$ ее образ в $Q{\text{/}}{{Q}_{r}}$, где ${{Q}_{r}}$ – разрешимый радикал в Q. Выберем произвольную точку $z$ из открытой $B$-орбиты в $X$ и обозначим через ${{Q}_{z}}$ ее стабилизатор в Q. Заметим, что $Qz \cap D \ne \emptyset $. Поскольку ${{Q}_{r}} \subset B$, естественный морфизм

факторизации по ${{Q}_{r}}$ индуцирует сохраняющую коразмерности биекцию между $B$-орбитами в Qz и $\bar {B}$-орбитами в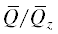 . В частности, 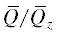содержит открытую $\bar {B}$-орбиту. Поскольку группа $\bar {Q}$ изоморфна либо ${\text{S}}{{{\text{L}}}_{2}}$, либо ${\text{PS}}{{{\text{L}}}_{2}}$, для ${{Q}_{z}}$ имеются следующие три возможности.

Тип $(U)$: ${{\bar {Q}}_{z}}$ содержит максимальную унипотентную подгруппу в $\bar {Q}$. В этом случае $Qz{{\backslash }}Bz$ есть одна $B$-орбита коразмерности 1, совпадающая с $Qz \cap D$.

Тип $(T)$: ${{\bar {Q}}_{z}}$ является максимальным тором в $\bar {Q}$. В этом случае $Qz\backslash Bz$ содержит две $B$-орбиты коразмерности 1, одна из которых совпадает с $Qz \cap D$.

Тип $(N)$: ${{\bar {Q}}_{z}}$ является нормализатором максимального тора в $\bar {Q}$. В этом случае $Qz{{\backslash }}Bz$ есть одна $B$-орбита коразмерности 1, совпадающая с $Qz\, \cap \,D$.

Известно, что определенный выше тип не зависит от выбора минимальной параболической подгруппы $Q \supset B$ с условием $QD \ne D$ (см. [3], Prop. 1). Это позволяет корректно определить тип для каждой краски в X.

Замечание 1. Определенные выше типы $(U)$, $(T)$, $(N)$ красок на X совпадают с типами $b$, $a$, $a{\text{'}}$ соответственно в обозначениях Лýны (см. [4, §§2.7, 3.4] или [5, §30.10]).

3. Как следует из [1, Prop. 1.6], для всякой B‑корневой подгруппы H на X существует не более одного дивизора $D \in {{\mathcal{D}}^{B}}$ с условием $HD \ne D$. Следующий результат обобщает [1, Cor. 4.25], где рассматривается частный случай аффинного X.

Предложение 1. Пусть B-корневая подгруппа H на X такова, что $HD \ne D$ для некоторого дивизора $D \in {{\mathcal{D}}^{B}}$. Тогда D либо G-инвариантен, либо является краской типа $(T)$.

Доказательство. Предположим, что D является краской одного из типов $(U)$ или (N), и выберем минимальную параболическую подгруппу $Q \supset B$ с условием $QD \ne D$. Тогда, в обозначениях п. 2, орбита Qz распадается на две $B$-орбиты ${{O}_{1}} = Bz$ и ${{O}_{2}} = O \cap D$. Из обсуждения в [1, § 1.5] вытекает, что в этом случае множество Qz является H-инвариантным, причем каждая H-орбита в Qz изоморфна аффинной прямой ${{\mathbb{A}}^{1}}$ и пересекает O₂ ровно в одной точке. Для каждой подгруппы $F \subset Q$ обозначим через $\tilde {F}$ ее образ в $Q{\text{/}}{{Q}_{u}}$, где ${{Q}_{u}}$ – унипотентный радикал в Q. По аналогии с (1), морфизм

факторизации по Q_u индуцирует сохраняющую коразмерности биекцию между B-орбитами в Qz и $\tilde {B}$-орбитами в $\tilde {Q}{\text{/}}{{\tilde {Q}}_{z}}$. Поскольку действия групп H и Q_u на $Qz$ коммутируют, на многообразии $\tilde {Q}{\text{/}}{{\tilde {Q}}_{z}}$ индуцируется нетривиальное действие группы $H$, нормализуемое действием группы $\tilde {B}$. В частности, в $\tilde {Q}{\text{/}}{{\tilde {Q}}_{z}}$ есть ровно две $\tilde {B}$-орбиты $\varphi ({{O}_{1}})$ и $\varphi ({{O}_{2}})$, а каждая $H$-орбита изоморфна ${{\mathbb{A}}^{1}}$ и пересекает $\varphi ({{O}_{2}})$ ровно в одной точке. Далее мы рассмотрим случаи типов $(U)$ и $(N)$ по отдельности. Условие на каждый из этих типов переформулировано с учетом того, что группа $\bar {Q}$ получается факторизацией группы $\tilde {Q}$ по своему связному центру.

Тип $(U)$: ${{\tilde {Q}}_{z}}$ содержит максимальную унипотентную подгруппу в $\tilde {Q}$. Тогда в $\tilde {Q}{\text{/}}{{\tilde {Q}}_{z}}$ найдется точка, неподвижная относительно унипотентного радикала ${{\tilde {B}}_{u}}$ группы $\tilde {B}$. Поскольку ${{\tilde {B}}_{u}}$ нормализуется группой $\tilde {B}$ и коммутирует с действием $H$, множество ${{\tilde {B}}_{u}}$-неподвижных точек в $\tilde {Q}{\text{/}}{{\tilde {Q}}_{z}}$ инвариантно относительно обеих групп $\tilde {B}$ и $H$, а значит, оно совпадает со всем $\tilde {Q}{\text{/}}{{\tilde {Q}}_{z}}$. Следовательно, ${{\tilde {B}}_{u}}$ действует на $\tilde {Q}{\text{/}}{{\tilde {Q}}_{z}}$ тривиально – противоречие.

Тип $(N)$: ${{\tilde {Q}}_{z}}$ содержит подгруппу $\tilde {Q}_{z}^{'}$ индекса 2, являющуюся прообразом связной компоненты единицы в ${{\bar {Q}}_{z}}$. Тогда естественный морфизм $\psi :\tilde {Q}{\text{/}}\tilde {Q}_{z}^{'} \to \tilde {Q}{\text{/}}{{\tilde {Q}}_{z}}$ представляет собой неразветвленное двулистное накрытие. Более того, множество ${{\psi }^{{ - 1}}}(\varphi ({{O}_{1}}))$ является открытой $\tilde {B}$-орбитой в $\tilde {Q}{\text{/}}\tilde {Q}_{z}^{'}$, а множество ${{\psi }^{{ - 1}}}(\varphi ({{O}_{2}}))$ распадается на две $\tilde {B}$-орбиты коразмерности 1, которые мы обозначим через ${{D}_{1}}$ и ${{D}_{2}}$. Пусть теперь $y = \varphi (z)$ и ${{\psi }^{{ - 1}}}(y) = \{ {{y}_{1}},{{y}_{2}}\} $. Так как $Hy \simeq {{\mathbb{A}}^{1}}$, то множество ${{\psi }^{{ - 1}}}(Hy)$ является несвязным объединением двух компонент ${{Y}_{1}}$ и ${{Y}_{2}}$, каждая из которых изоморфно отображается на $Hy$. Без ограничения общности будем считать, что ${{y}_{i}} \in {{Y}_{i}}$ при $i = 1,\;2$. Пусть элемент $b \in \tilde {B}$ таков, что $b{{y}_{1}} = {{y}_{2}}$. Тогда $b \in {{\tilde {B}}_{z}}$ и, значит, $b{{y}_{2}} = {{y}_{1}}$. В силу $\tilde {B}$-инвариантности орбиты $Hy$ получаем, что действие элемента b переставляет множества ${{Y}_{1}}$ и ${{Y}_{2}}$. С другой стороны, множество ${{\psi }^{{ - 1}}}(Hy \cap \varphi ({{O}_{2}}))$ состоит из двух точек, принадлежащих разным $\tilde {B}$-орбитам – противоречие.

В терминологии [1, § 4.2], $B$-корневая подгруппа $H$ на $X$ называется вертикальной, если она сохраняет открытую $B$-орбиту, и горизонтальной в противном случае. Если $H$ горизонтальна и $HD \ne D$ для некоторого $D \in {{\mathcal{D}}^{B}}$, то будем говорить, что $H$ двигает $D$. В соответствии с предложением 1 горизонтальные $B$-корневые подгруппы можно разделить на два типа.

Определение 1. Пусть $H$ – горизонтальная $B$-корневая подгруппа на $X$, и пусть дивизор $D \in {{\mathcal{D}}^{B}}$ таков, что $HD \ne D$. Если $D \in {{\mathcal{D}}^{G}}$, то назовем $H$ тороидальной. Если $D$ является краской типа $(T)$, то назовем $H$ размывающей.

4. Для всякого подмножества $\mathcal{F} \subset \mathcal{D}$ положим ${{D}_{\mathcal{F}}} = \bigcup\limits_{D \in \mathcal{F}} D $, ${{X}_{\mathcal{F}}} = X{{\backslash }}{{D}_{\mathcal{F}}}$ и обозначим через ${{P}_{\mathcal{F}}}$ стабилизатор в $G$ множества ${{X}_{\mathcal{F}}}$. Тогда ${{P}_{\mathcal{F}}}$ – параболическая подгруппа в $G$, содержащая $B$. Ключевую роль в наших дальнейших рассмотрениях играет теорема о локальной структуре (см. [7, Thm. 2.3, Prop. 2.4], [8, Thm. 1.4]), которая в нашей ситуации формулируется следующим образом.

Теорема 1. Пусть $\mathcal{F} \subset \mathcal{D}$ – произвольное подмножество и $P = L \rightthreetimes {{P}_{u}}$ – разложение Леви группы $P = {{P}_{\mathcal{F}}}$. Тогда существует замкнутое $L$-инвариантное подмногообразие $Z \subset {{X}_{\mathcal{F}}}$, для которого отображение ${{P}_{u}} \times Z \to {{X}_{\mathcal{F}}}$, заданное формулой $(p,z) \mapsto pz$, является $P$-эквивариантным изоморфизмом, где действие $P$ на ${{P}_{u}} \times Z$ определяется по формуле $lu(p,z) = (lup{{l}^{{ - 1}}},lz)$ для всех $l \in L$, $u,p \in {{P}_{u}}$, $z \in Z$. Более того, если $P$ совпадает со стабилизатором открытой $B$-орбиты в $X$, то коммутант группы $L$ действует на $Z$ тривиально.

Ниже нам также понадобится следующее наблюдение.

Предложение 2. Пусть $\mathcal{F} = \mathcal{D}$ или $\mathcal{F}$ = = $\mathcal{D}{{\backslash }}\{ {{D}_{0}}\} $, где ${{D}_{0}}$ – краска типа $(T)$. Тогда группа ${{P}_{\mathcal{F}}}$ совпадает со стабилизатором открытой $B$-орбиты в $X$.

Доказательство. В случае $\mathcal{F} = \mathcal{D}$ утверждение очевидно, поэтому далее считаем $\mathcal{F}$ = = $\mathcal{D}{{\backslash }}\{ {{D}_{0}}\} $ для некоторой краски ${{D}_{0}}$ типа $(T)$. Пусть $Q \supset B$ – произвольная минимальная параболическая подгруппа в G. Тогда условие $Q{{D}_{0}} \ne {{D}_{0}}$ может выполняться только в том случае, если $QD{\text{'}} \ne D{\text{'}}$ для некоторой краски $D{\text{'}} \in \mathcal{D}{{\backslash }}\{ {{D}_{0}}\} $. Значит, если $Q \subset {{P}_{\mathcal{F}}}$, то $Q{{D}_{0}} = {{D}_{0}}$. Поскольку ${{P}_{\mathcal{F}}}$ порождается как группа всеми содержащимися в ней минимальными параболическими подгруппами, мы получаем ${{P}_{\mathcal{F}}}{{D}_{0}} = {{D}_{0}}$, откуда и следует требуемое.

5. С этого момента и до конца работы будем предполагать, что $X$ – аффинное сферическое $G$‑многообразие. Введем некоторые обозначения.

Зафиксируем максимальный тор $T \subset B$ и обозначим через $\mathfrak{X}(T)$ его решетку характеров. Пусть $\Delta \subset \mathfrak{X}(T)$ – система корней группы $G$ относительно $T$ и ${{\Lambda }^{ + }} \subset \mathfrak{X}(T)$ – моноид доминантных весов относительно $B$.

Пусть $M$ (соответственно $\Gamma $) – решетка (соответственно моноид) весов $B$-полуинвариантных рациональных (соответственно регулярных) функций на $X$. В силу аффинности $X$ имеем $M = \mathbb{Z}\Gamma $ (см., например, [5, Prop. 5.14]). Рассмотрим двойственную решетку $N = {\text{Ho}}{{{\text{m}}}_{\mathbb{Z}}}(M,\mathbb{Z})$ и соответствующее рациональное векторное пространство ${{N}_{\mathbb{Q}}} = N{{ \otimes }_{\mathbb{Z}}}\mathbb{Q}$. Естественное спаривание $N \times M \to \mathbb{Z}$ будем обозначать через $\langle \cdot {\kern 1pt} , \cdot \rangle $.

Поскольку в $X$ есть открытая $B$-орбита, для каждого $\lambda \in M$ существует единственная с точностью до пропорциональности $B$-полуинвариантная рациональная функция ${{f}_{\lambda }}$ на $X$ веса $\lambda $. Потребовав, чтобы все такие функции принимали значение 1 в фиксированной точке открытой $B$‑орбиты, будем считать, что ${{f}_{\lambda }}{{f}_{\mu }} = {{f}_{{\lambda + \mu }}}$ для всех $\lambda ,\mu \in M$. Каждый дивизор $D \in {{\mathcal{D}}^{B}}$ определяет элемент $\varkappa (D) \in N$ по формуле $\langle \varkappa (D),\lambda \rangle = {\text{or}}{{{\text{d}}}_{D}}({{f}_{\lambda }})$ для всех $\lambda \in M$. В силу нормальности многообразия $X$ имеем

В частности, множество $\{ \varkappa (D)|D \in {{\mathcal{D}}^{B}}\} $ порождает строго выпуклый конус в ${{N}_{\mathbb{Q}}}$.

Для каждого строго выпуклого конуса $\mathcal{C} \subset {{N}_{\mathbb{Q}}}$ обозначим через ${{\mathcal{C}}^{1}}$ множество примитивных элементов $\rho $ решетки $N$, для которых луч ${{\mathbb{Q}}_{{ \geqslant 0}}}\rho $ является гранью конуса $\mathcal{C}$. Для каждого $\rho \in {{\mathcal{C}}^{1}}$ определим множество

Элементы множества $\Re (\mathcal{C}) = \coprod\limits_{\rho \in {{\mathcal{C}}^{1}}} {{{\Re }_{\rho }}} (\mathcal{C})$ называются корнями Демазюра конуса $\mathcal{C}$. Положим

и рассмотрим алгебру $A(\mathcal{C}) = \mathop \oplus \limits_{\lambda \in \Gamma (\mathcal{C})} \mathbb{K}{{f}_{\lambda }}$. В дальнейшем нам понадобится следующий хорошо известный результат (см. [9, Thm. 2.7]), дающий описание всех $T$-нормализуемых ЛНД на алгебре $A(\mathcal{C})$.

Теорема 2. Пусть $\mathcal{C} \subset {{N}_{\mathbb{Q}}}$ – произвольный строго выпуклый конус.

(a) Множество весов всех T-нормализуемых ЛНД на $A(\mathcal{C})$ есть $\Re (\mathcal{C})$;

(б) Для каждого $\rho \in {{\mathcal{C}}^{1}}$ и каждого $\mu \in {{\Re }_{\rho }}(\mathcal{C})$ существует единственное с точностью до пропорциональности T-нормализуемое ЛНД ${{\partial }_{\mu }}$ на $A(\mathcal{C})$ веса $\mu $, задаваемое формулой

для всех $\lambda \in \Gamma (\mathcal{C})$.

6. Пусть $H$ – $B$-корневая подгруппа на $X$ и ${{\mathcal{F}}_{H}} = \{ D \in \mathcal{D}|HD = D\} $. Тогда $H$ сохраняет открытое подмножество ${{X}_{{{{\mathcal{F}}_{H}}}}} \subset X$ и тем самым определяет $B$-нормализуемое ЛНД на алгебре $\mathbb{K}[{{X}_{{{{\mathcal{F}}_{H}}}}}]$. Заметим, что ${{\mathcal{F}}_{H}} = \mathcal{D}$ в случае вертикальной или тороидальной $H$ и ${{\mathcal{F}}_{H}} = \mathcal{D}{{\backslash }}\{ {{D}_{0}}\} $ в случае размывающей $H$, двигающей краску ${{D}_{0}}$ типа $(T)$.

Пусть теперь $\mathcal{F} = \mathcal{D}$ или $\mathcal{F} = \mathcal{D}{{\backslash }}\{ {{D}_{0}}\} $, где ${{D}_{0}} \in \mathcal{D}$ – краска типа $(T)$. Наша цель в данном пункте – описать все $B$-нормализуемые ЛНД на алгебре $\mathbb{K}[{{X}_{\mathcal{F}}}]$.

Применим теорему 1 и сохраним обозначения $Z$, $L$, ${{P}_{u}}$, используемые в этой теореме. Тогда имеется P-эквивариантный изоморфизм ${{X}_{\mathcal{F}}} \simeq {{P}_{u}} \times Z$, по которому мы будем отождествлять эти два многообразия в дальнейшем. Без ограничения общности будем считать, что $L \supset T$. В силу предложения 2 коммутант группы $L$ действует три-виально на $Z$. Поскольку ${{X}_{\mathcal{F}}}$ содержит открытую $B$-орбиту, многообразие $Z$ содержит открытую $T$-орбиту, которую мы обозначим через ${{Z}_{0}}$. Зафиксируем также произвольную точку ${{z}_{0}} \in {{Z}_{0}}$. Обозначим через ${{L}_{0}}$ ядро действия группы $L$ на $Z$ и положим ${{T}_{0}} = T \cap {{L}_{0}}$. Заметим, что $M$ состоит в точности из всех характеров тора $T$, ограничение которых на ${{T}_{0}}$ тривиально.

Для всякого $\lambda \in M$ ограничение функции ${{f}_{\lambda }}$ на подмногообразие $Z$ является $T$-полуинвариантной рациональной функцией, которую мы будем обозначать тем же символом ${{f}_{\lambda }}$. Тогда $\mathbb{K}[Z] = \mathop \oplus \limits_{\lambda \in {{\Gamma }_{Z}}} \mathbb{K}{{f}_{\lambda }}$, где

Без ограничения общности будем считать, что ${{f}_{\lambda }}({{z}_{0}}) = 1$ для всех $\lambda \in M$.

Рассмотрим присоединенное представление группы L в пространстве ${{\mathfrak{p}}_{u}} = {\text{Lie}}{{P}_{u}}$ и разложим ${{\mathfrak{p}}_{u}}$ в прямую сумму неприводимых L-инвариантных подпространств. Хорошо известно (см. [6, Thm. 0.1]), что все входящие в данное разложение слагаемые попарно неизоморфны как L-модули; пусть $\Omega \subset \Delta $ – множество старших весов этих слагаемых относительно борелевской подгруппы $B \cap L \subset L$. Для каждого $\alpha \in \Omega $ зафиксируем ненулевой вектор ${{e}_{\alpha }} \in {{\mathfrak{p}}_{u}}$ веса $\alpha $. Действие группы ${{P}_{u}}$ на себе умножениями справа индуцирует действие алгебры Ли ${{\mathfrak{p}}_{u}}$ на алгебре $\mathbb{K}[{{P}_{u}}]$; для каждого $\alpha \in \Omega $ обозначим через ${{\delta }_{\alpha }}$ дифференцирование алгебры $\mathbb{K}[{{P}_{u}}]$, определяемое действием элемента ${{e}_{\alpha }}$. Это дифференцирование $B$-инвариантно веса α, автоматически локально нильпотентно и соответствует действию группы $\{ \exp (t{{e}_{\alpha }})|t \in \mathbb{K}\} $ на ${{P}_{u}}$ умножениями справа. Будем рассматривать ${{\delta }_{\alpha }}$ как ЛНД на всей алгебре $\mathbb{K}[{{P}_{u}} \times Z] \simeq \mathbb{K}[{{P}_{u}}]{{ \otimes }_{\mathbb{K}}}\mathbb{K}[Z]$, полагая ${{\delta }_{\alpha }}(\mathbb{K}[Z]) = 0$.

Для каждого характера $\mu \in \mathfrak{X}(T)$ положим

Отметим, что условие ${{\left. \mu \right|}_{{{{T}_{0}}}}} = {{\left. \alpha \right|}_{{{{T}_{0}}}}}$ равносильно $\mu - \alpha \in M$.

Теорема 3. Всякое $B$-нормализуемое ЛНД веса $\mu $ на алгебре $\mathbb{K}[{{P}_{u}} \times Z]$ имеет вид

где ${{c}_{\alpha }} \in \mathbb{K}$ и ${{\partial }_{Z}}$ – некоторое T-нормализуемое ЛНД веса μ на $\mathbb{K}[Z]$, продолженное тривиально на $\mathbb{K}[{{P}_{u}}]$. Обратно, всякое дифференцирование на $\mathbb{K}[{{P}_{u}} \times Z]$ указанного вида является $B$-нормализуемым веса $\mu $ и локально нильпотентным.

Доказательство. Пусть $\partial $ – $B$-нормализуемое ЛНД веса $\mu $ на $\mathbb{K}[{{P}_{u}} \times Z]$, и пусть ${{\partial }_{Z}}$ – ограничение $\partial $ на подалгебру $\mathbb{K}[Z]$. Далее будем рассматривать ${{\partial }_{Z}}$ как дифференцирование на всей алгебре $\mathbb{K}[{{P}_{u}} \times Z]$, полагая ${{\partial }_{Z}}(\mathbb{K}[{{P}_{u}}]) = 0$. Продолжение дифференцирования $\partial - {{\partial }_{Z}}$ на алгебру $\mathbb{K}[{{P}_{u}} \times {{Z}_{0}}]$ задает $B$-полуинвариантное веса $\mu $ векторное поле $\xi $ на гладком многообразии ${{P}_{u}} \times {{Z}_{0}}$. Поскольку группа $B$ действует на ${{P}_{u}} \times {{Z}_{0}}$ транзитивно, $\xi $ однозначно определяется своим значением ${v}$ в точке $(e,{{z}_{0}})$, где $e \in {{P}_{u}}$ – единичный элемент. Так как $\partial - {{\partial }_{Z}}$ действует тривиально на $\mathbb{K}[{{Z}_{0}}]$, то ${v}$ является $B \cap {{L}_{0}}$-полуинвариантным вектором в ${{\mathfrak{p}}_{u}}$ веса ${{\left. \mu \right|}_{{{{T}_{0}}}}}$, а значит, ${v} = \sum\limits_{\alpha \in {{\Omega }_{\mu }}}^{} {{{c}_{\alpha }}{{e}_{\alpha }}} $ для некоторых ${{c}_{\alpha }} \in \mathbb{K}$. С другой стороны, заметим, что дифференцирование $\sum\limits_{\alpha \in {{\Omega }_{\mu }}}^{} {{{c}_{\alpha }}{{f}_{{\mu - \alpha }}}{{\delta }_{\alpha }}} $ на $\mathbb{K}[{{Z}_{0}}]$ также B-полуинвариантно веса $\mu $ и соответствует тому же касательному вектору в точке $(e,{{z}_{0}})$, потому оно совпадает с $\partial - {{\partial }_{Z}}$. Поскольку данное дифференцирование сохраняет алгебру $\mathbb{K}[{{P}_{u}} \times Z]$, должно выполняться ${{c}_{\alpha }} = 0$ для всех $\alpha \in {{\Omega }_{\mu }}$ с условием $\mu - \alpha \notin {{\Gamma }_{Z}}$, что и доказывает первое утверждение.

Пусть теперь $\partial $ – дифференцирование на $\mathbb{K}[{{P}_{u}} \times Z]$ вида (9). Тогда $\partial $ автоматически B-нормализуемо веса μ, и нам остается проверить, что $\partial $ локально нильпотентно. Поскольку $\mathbb{K}[{{P}_{u}}]$ является рациональным ${{P}_{u}}$-модулем (относительно действия справа), достаточно проверить локальную нильпотентность $\partial $ на произвольном подпространстве вида $V{{ \otimes }_{\mathbb{K}}}\mathbb{K}[Z]$, где $V \subset \mathbb{K}[{{P}_{u}}]$ – конечномерное ${{P}_{u}}$-инвариантное подпространство. Так как образ алгебры ${{\mathfrak{p}}_{u}}$ в $\mathfrak{g}\mathfrak{l}(V)$ нильпотентен, то в $V$ существует флаг подпространств

со свойством ${{\mathfrak{p}}_{u}}{{V}_{i}} \subset {{V}_{{i - 1}}}$ для всех $i = 1,\; \ldots ,\;s$. Отсюда следует, что для всех $i = 1,\; \ldots ,\;s$, $g \in {{V}_{i}}$ и $f \in \mathbb{K}[Z]$ имеем поскольку ${{\delta }_{\alpha }}(g) = {{e}_{\alpha }}g \in {{V}_{{i - 1}}}$ для всех $\alpha \in \Omega $. Так как ${{\partial }_{Z}}$ – ЛНД на $\mathbb{K}[Z]$, то получаем ${{\partial }^{k}}(gf) \in {{V}_{{i - 1}}}{{ \otimes }_{\mathbb{K}}}\mathbb{K}[Z]$ для некоторого k > 0. Доказательство завершается применением индукции по i.

7. Сохраним предположения и обозначения предыдущего пункта. Теперь изучим вопрос, когда $B$-нормализуемое ЛНД на алгебре $\mathbb{K}[{{P}_{u}} \times Z]$ сохраняет подалгебру $\mathbb{K}[X]$ и тем самым определяет $B$-корневую подгруппу на всем многообразии X. Пусть $\lambda \mapsto \overline \lambda $ – произвольный оператор проектирования пространства $\mathfrak{X}(T){{ \otimes }_{\mathbb{Z}}}\mathbb{Q}$ на подпространство $M{{ \otimes }_{\mathbb{Z}}}\mathbb{Q}$. Пусть также ${{\mathcal{E}}_{Z}} \subset {{N}_{\mathbb{Q}}}$ – конус, порожденный множеством $\{ \kappa (D)|D \in {{\mathcal{D}}^{B}}{{\backslash }}\mathcal{F}\} $, так что ${{\Gamma }_{Z}} = \Gamma ({{\mathcal{E}}_{Z}})$ в силу (7) и $\mathbb{K}[Z] = A({{\mathcal{E}}_{Z}})$ (см. обозначения в п. 5).

Теорема 4. Существует набор констант $\{ {{C}_{D}}|D \in \mathcal{F}\} $ со следующим свойством: если $\mu \in \mathfrak{X}(T)$ и $\langle {{\nu }_{D}},\bar {\mu }\rangle \geqslant {{C}_{D}}$ для всех $D \in \mathcal{F}$, то всякое $B$-нормализуемое ЛНД на $\mathbb{K}[{{P}_{u}} \times Z]$ веса $\mu $ сохраняет $\mathbb{K}[X]$.

Доказательство. Пусть ${{F}_{1}},\; \ldots ,\;{{F}_{k}}$ – фиксированная система порождающих алгебры $\mathbb{K}[X]$. Для каждого $i = 1,\; \ldots ,\;k$ имеем ${{F}_{i}} = \sum\limits_{j = 1}^{{{n}_{i}}} {{{g}_{{ij}}}{{f}_{{{{\lambda }_{{ij}}}}}}} $ для некоторых функций ${{g}_{{ij}}} \in \mathbb{K}[{{P}_{u}}]$ и весов ${{\lambda }_{{ij}}} \in {{\Gamma }_{Z}}$. Если $\partial $ – произвольное дифференцирование алгебры $\mathbb{K}[{{P}_{u}} \times Z]$, то $\partial $ сохраняет $\mathbb{K}[X]$ тогда и только тогда, когда ${\text{or}}{{{\text{d}}}_{D}}(\partial ({{F}_{i}})) \geqslant 0$ для всех $D \in \mathcal{F}$ и $i = 1,\; \ldots ,\;k$.

Чтобы подобрать требуемый набор констант, в силу теоремы 3 для каждого веса $\mu \in \mathfrak{X}(T)$ достаточно потребовать, чтобы каждое слагаемое в сумме (9) сохраняло $\mathbb{K}[X]$.

Для всех $D \in \mathcal{F}$, $i = 1,\; \ldots ,\;k$ и $\alpha \in \Omega _{\mu }^{0}$ при ${{\delta }_{\alpha }}({{F}_{i}}) \ne 0$ имеем

Если ${{\partial }_{Z}} \ne 0$, то по теореме 2 имеем $\mu \in {{\Re }_{\rho }}({{\mathcal{E}}_{Z}})$ для некоторого $\rho \in \mathcal{E}_{Z}^{1}$ (в частности, $\mu \in M$ и $\bar {\mu } = \mu $) и существует такая ненулевая константа $c \in \mathbb{K}$, что ${{\partial }_{Z}}({{f}_{\lambda }}) = c\langle \rho ,\lambda \rangle {{f}_{\lambda }}{{f}_{\mu }}$ для всех $\lambda \in {{\Gamma }_{Z}}$. Тогда для всех $D \in \mathcal{F}$ и $i = 1,\; \ldots ,\;k$ при ${{\partial }_{Z}}({{F}_{i}}) \ne 0$ имеем

Остается заметить, что все выражения в (12) и (13) будут неотрицательны при подходящем выборе искомых констант.

8. Выведем несколько следствий из теорем 3 и 4.

Следствие 1. Все $B$-нормализуемые ЛНД на $\mathbb{K}[X]$ одного веса образуют конечномерное векторное пространство над $\mathbb{K}$.

Доказательство. В силу [1, Prop. 4.22] любые две горизонтальных B-корневых подгруппы на X одного и того же веса $\mu $ двигают один и тот же дивизор $D \in {{\mathcal{D}}^{B}}$. Следовательно, в условиях п. 6 можно подобрать такое подмножество $\mathcal{F} \subset \mathcal{D}$, что все B-корневые подгруппы на X веса $\mu $ сохраняют ${{X}_{\mathcal{F}}}$. По теоремам 3 и 2 все B-нормализуемые ЛНД на $\mathbb{K}[{{X}_{\mathcal{F}}}]$ веса $\mu $ образуют конечномерное векторное пространство. Условие сохранения подалгебры $\mathbb{K}[X]$ выделяет подпространство в данном векторном пространстве.

Пусть $\mathcal{E} \subset {{N}_{\mathbb{Q}}}$ – конус, порожденный множеством $\{ \varkappa (D)|D \in {{\mathcal{D}}^{B}}\} $, так что $\Gamma = \Gamma (\mathcal{E})$ в силу (3).

Следствие 2. Пусть $D \in {{\mathcal{D}}^{B}}$, причем либо $D \in {{\mathcal{D}}^{G}}$, либо D является краской типа $(T)$. Предположим, что существует элемент $\rho \in {{\mathcal{E}}^{1}}$ с условиями $\varkappa (D) \in {{\mathbb{Q}}_{{ \geqslant 0}}}\rho $ и $\varkappa (D{\text{'}}) \notin {{\mathbb{Q}}_{{ \geqslant 0}}}\rho $ для всех $D{\text{'}} \in {{\mathcal{D}}^{B}}{{\backslash }}\{ D\} $. Тогда существует B-корневая подгруппа на $X$, двигающая D.

Доказательство. Положим $\mathcal{F} = \mathcal{D}$ при $D \in {{\mathcal{D}}^{G}}$ и $\mathcal{F} = \mathcal{D}{{\backslash }}\{ D\} $ иначе. Сохраним обозначения пп. 6 и 7. Поскольку $\rho \in {{\mathcal{E}}_{Z}}$ и ${{\mathcal{E}}_{Z}} \subset \mathcal{E}$, имеем $\rho \in \mathcal{E}_{Z}^{1}$. Выберем любой элемент $\mu \in {{\Re }_{\rho }}({{\mathcal{E}}_{Z}})$ и рассмотрим B-нормализуемое ЛНД ${{\partial }_{\mu }}$ на $\mathbb{K}[{{P}_{u}} \times Z]$ веса $\mu $, действующее тривиально на $\mathbb{K}[{{P}_{u}}]$ и по формуле (6) на $\mathbb{K}[Z]$. Из условия следует, что существует вес $\lambda \in \Gamma $ со свойствами $\langle \rho ,\lambda \rangle = 0$ и $\langle \varkappa (D{\text{'}}),\lambda \rangle > 0$ для всех $D{\text{'}} \in \mathcal{F}$. Тогда для всех целых $N > 0$ имеем $N\lambda + \mu \in {{\Re }_{\rho }}({{\mathcal{E}}_{Z}})$. По теореме 4 найдется такое значение ${{N}_{0}}$, что при всех $N \geqslant {{N}_{0}}$ ЛНД ${{\partial }_{{N\lambda + \mu }}} = {{f}_{{N\lambda }}}{{\partial }_{\mu }}$ сохраняет подалгебру $\mathbb{K}[X]$ и тем самым определяет $B$-корневую подгруппу на X. Эта $B$-корневая подгруппа двигает $D$ в силу [1, Prop. 4.22].

Ввиду [1, Prop. 3.9] всякий дивизор $D \in {{\mathcal{D}}^{G}}$ автоматически удовлетворяет условию следствия 2. Отсюда вытекает следующий результат, который был сформулирован в качестве гипотезы в [1, Conj. 4.29].

Следствие 3. Для всякого $D \in {{\mathcal{D}}^{G}}$ существует $B$-корневая подгруппа на X, двигающая D.