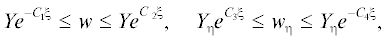Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 503, № 1, стр. 33-39

ВВЕДЕНИЕ

В работе рассматривается магнитогидродинамический пограничный слой жидкости с нелинейным реологическим уравнением О.А. Ладыженской. В работах [1–3] такая система была изучена с использованием преобразования Мизеса, а в работах [4, 5] – с помощью преобразования Крокко (о преобразованиях Мизеса и Крокко см. [6]). О поведении электропроводных жидкостей см. [7]. Другие задачи гидродинамики реологически сложных сред см. [8–12], в которых доказаны теоремы существования и единственности для систем, описывающих поведение жидких кристаллов – нематиков.

В настоящей работе изучены движение жидкости в конфузоре (трубе переменного сечения) и поведение соответствующего пограничного слоя, начиная с носовой точки конфузора.

1. ПОСТАНОВКА ЗАДАЧИ И ПРЕОБРАЗОВАНИЕ КРОККО

Рассматривается двумерное стационарное течение модифицированной вязкой жидкости, подчиняющейся реологическому закону О.А. Ладыженской. В этом случае система уравнений Прандтля имеет вид

Здесь $\nu $, d – постоянные, зависящие от свойств жидкости, плотность жидкости $\rho $ предполагается равной единице, $B(x)$, $U(x)$ – заданные достаточно гладкие функции. Функция скорости внешнего потока $U(x)$ связана с давлением $p(x)$ и компонентами электрического поля $B(x)$ соотношением

Система уравнений (1) рассматривается в области $D = \{ 0 < x < X,0 < y < \infty \} $ с граничными условиями

где $U(0) = 0$, $U(x) > 0{\kern 1pt} $ при ${\kern 1pt} x > 0$. Пусть ${{U}_{x}}(0) > 0$. Условия $U(0) = 0$ и $u(0,y) = 0$ определяют точку x = 0 как точку, в которой происходит остановка внешнего потока жидкости (носовая точка обтекаемого тела) и пограничный слой симметричен относительно этой точки.

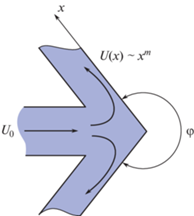
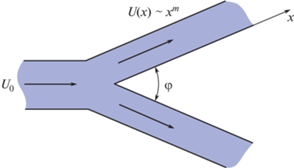
О внешнем потоке в окрестности носовой точки обтекаемого тела известно, что скорость потока меняется по закону $U(x) \sim C{{x}^{m}}$, где $C,m$ = const > 0, причем m зависит от угла $\varphi = 2\pi \frac{m}{{m + 1}}$ между образующими обтекаемой поверхности в точке x = 0, см. [13].

В работе [4] в аналогичных задачах предполагалось $m = 1$, т.е. пограничный слой рассматривался в окрестности затупленной носовой точки обтекаемого тела.

Определение 1. Классическим решением задачи (1), (2) называются функции $u(x,y)$ и ${v}(x,y)$, обладающие следующими свойствами: $u(x,y)$ непрерывна в замкнутой области $\overline D $, ${v}(x,y)$ непрерывна в $D$, а по $y{\kern 1pt} $ в $\overline D $; функции $u(x,y)$ и ${v}(x,y)$ имеют в $D$ непрерывные производные, входящие в уравнение (1); $u(x,y)$ и ${v}(x,y)$ удовлетворяют поточечно уравнениям (1) и граничным условиям (2).

Задачу (1), (2) сводим к краевой задаче для одного квазилинейного уравнения с помощью замены переменных $(x,y) \to (\xi ,\eta )$ и введения новой неизвестной функции $w(\xi ,\eta )$, где

После преобразований получаем одно квазилинейное уравнение

в области $\Omega = \{ 0 < \xi < X,0 < \eta < 1\} $ с граничными условиями

Определение 2. Функция $w(\xi ,\eta )$ называется решением задачи (4), (5), если $w$ непрерывна в $\bar {\Omega }$ и имеет непрерывные производные ${{w}_{\xi }},{{w}_{\eta }},{{w}_{{\eta \eta }}}$ в Ω; ${{w}_{\eta }}$ непрерывна по $\eta $ при $\eta = 0$; w удовлетворяет уравнению (4) в $\Omega $ и граничным условиям (5).

Предположим дополнительно, что U(x) = = ${{x}^{m}}V(x),$ $V(x) > 0$ при $0 \leqslant x \leqslant X$, ${{{v}}_{0}}(x)\, = \,{{x}^{{\frac{{m - 1}}{2}}}}{{{v}}_{1}}(x)$, $V(x) = a + x{{a}_{1}}(x)$, a > 0, ${{{v}}_{1}}(x) = b + x{{b}_{1}}(x)$, ${{a}_{1}}(x)$ и ${{b}_{1}}(x)$ достаточно гладкие функции. Перейдем от функции $w(\xi ,\eta )$ к функции $w(\xi ,\eta ){{\xi }^{{\frac{{m - 1}}{2}}}}$, сохранив прежнее обозначение.

Получим уравнение

в области $\Omega = \{ 0 < \xi < X,0 < \eta < 1\} $ с граничными условиями

2. ОСНОВНЫЕ ТЕОРЕМЫ

Рассмотрим вспомогательную граничную задачу для обыкновенного дифференциального уравнения

с граничными условиями

В работе доказываются следующие утверждения.

Теорема 1. Пусть ${{V}_{x}} > 0$ и функции ${{a}_{1}}(x)$, ${{a}_{1}}_{x}(x)$, ${{a}_{1}}_{{xx}}(x)$, ${{b}_{1}}(x)$, ${{b}_{1}}_{x}(x)$ ограничены при $0\, \leqslant \,x\, \leqslant \,X$. Тогда задача (4), (5) в области $\Omega $, где X зависит от U, ${{{v}}_{0}}$, $\nu $, имеет положительное при $\eta < 1$ решение, обладающее следующими свойствами: $w(\xi ,\eta )$ непрерывна в $\bar {\Omega }$; обобщенные производные ${{w}_{\xi }}$, ${{w}_{\eta }}$, ${{w}_{{\eta \eta }}}$ существуют и удовлетворяют неравенствам

В любой замкнутой области, лежащей внутри $\Omega $, функция w и ее производные, входящие в уравнение (4), удовлетворяют условию Гёльдера.

Теорема 2. Задача (4), (5) в области $\Omega $ может иметь лишь одно неотрицательное решение $w$, обладающее следующими свойствами: $w$ непрерывна в $\Omega $; ${{w}_{\eta }}$, ${{w}_{{\eta \eta }}}$, ${{w}_{\xi }}$ непрерывны во внутренних точках $\Omega $; $w > 0$ при $\eta = 0$; ${{w}_{\eta }}$ непрерывна по $\eta $ при $\eta = 0$.

Теорема 3. Пусть ${{V}_{x}} > 0$ и функции ${{a}_{1}}(x)$, ${{a}_{1}}_{x}(x)$, ${{a}_{1}}_{{xx}}(x)$, ${{b}_{1}}(x)$, ${{b}_{1}}_{x}(x)$ ограничены при $0\, \leqslant \,x\, \leqslant \,X$. Тогда задача (1), (2) в области $D$, при X, зависящем от $U$ и ${{{v}}_{0}}$, имеет решение u, ${v}$, которое обладает следующими свойствами: ${{u}_{y}} > 0$ при $y \geqslant 0$ и $x > 0$; функции $\frac{u}{U}$, $\frac{{{{u}_{y}}}}{{{{x}^{{\frac{{m - 1}}{2}}}}U}}$ ограничены и непрерывны в $\bar {D}$; $u > 0$ при $y > 0$ и $x > 0$; $u \to U$ при $y \to \infty $, $u(x,0) = u(0,y) = 0$; $\frac{{{{u}_{y}}}}{U} > 0$ при $y \geqslant 0$; $\frac{{{{u}_{y}}}}{U} \to 0$ при $y \to \infty $; ${{u}_{x}}$, ${{u}_{y}}$, ${{u}_{{yy}}}$ ограничены и непрерывны в $\bar {D}$; ${v}$ непрерывна в $\bar {D}$ по $y$ при $x > 0$; ${v}$ непрерывна по x и y внутри D; ${{u}_{{yyy}}}$ ограничена в $\bar {D}$; ${{u}_{{xy}}}$ ограничена в $D$ при ограниченных y; ${{u}_{{xy}}}$ и ${{u}_{{yyy}}}$ непрерывны в $\bar {D}$; $\frac{{{{u}_{{yy}}}}}{{{{x}^{{\frac{{m - 1}}{2}}}}{{u}_{y}}}}$ непрерывна в $\bar {D}$ по y; имеют место оценки

где $Y(\eta )$ – решение задачи (8), (9).

Теорема 4. Пусть $u$, ${v}$ – решение задачи (1), (2) такое, что: производные ${{u}_{x}}$, ${{u}_{y}}$, ${{{v}}_{y}}$, ${{u}_{{yy}}}$, ${{u}_{{yyy}}}$, ${{u}_{{xy}}}$ непрерывны в D; $\frac{u}{U}$ и $\frac{{{{u}_{y}}}}{{{{x}^{{\frac{{m - 1}}{2}}}}U}}$ непрерывны в $\bar {D}$; ${{u}_{y}} > 0$ при $y \geqslant 0$, $x > 0$; $\frac{{{{u}_{y}}}}{U} > 0$ при $y = 0$; $\frac{{{{u}_{y}}}}{U} \to 0$ при $y \to \infty $; $\frac{{{{u}_{{yy}}}}}{{{{x}^{{\frac{{m - 1}}{2}}}}{{u}_{y}}}}$, u_x непрерывны по $y$ при $y = 0$; $\frac{{{{u}_{{yyy}}}{{u}_{y}} - u_{y}^{2}}}{{u_{y}^{2}}} \leqslant 0$.

Тогда $u$, ${v}$ – единственное решение задачи (1), (2) с указанными свойствами.

Предполагаем далее, что имеют место следующие асимптотики:

где $a = {\text{const}} > 0$; ${{a}_{\beta }} = {\text{const}}$; $\beta = 1,\; \ldots ,\;q$; $b$, ${{b}_{\gamma }} = {\text{const}}$; $\gamma = 1,\; \ldots ,\;q$;

Эти предположения выполняются, в частности, когда производная порядка $q + l + 1$ функции $U(x)$ и производная порядка $q + l$ функции ${{{v}}_{0}}(x)$ ограничены.

Рассмотрим семейство задач

Здесь ${{Y}_{0}}(\eta )$ – решение задачи (8), (9).

Теорема 5. Предположим, что для $U(x)$ и ${{{v}}_{0}}(x)$ имеем представления (12) при $q \geqslant 1$. Тогда для решения $w(\xi ,\eta )$ задачи (4), (5) справедливо асимптотическое разложение вида

при $\xi \to 0$, где ${{Y}_{l}}$, $l = 1,\; \ldots ,\;q$ – решения задачи (13), (14); ${{Y}_{0}}$ – решение уравнения (8) с условиями (9); C₁₃– положительная постоянная.

Теорема 6. Предположим, что имеют место равенства (12) при $q \geqslant 1$. Тогда для решения $u$, ${v}$ задачи (1), (2) справедлива оценка

где ${{Y}_{m}}$, $m = 1,\; \ldots ,\;q$ – решения задачи (13), (14).

3. ДОКАЗАТЕЛЬСТВО СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ РЕШЕНИЯ ЗАДАЧИ

Теоремы 1 и 2 могут быть доказаны с применением методов работы [4] (см. также [14]). Доказательство теоремы 1 проводится методом прямых, т.е. в уравнении задачи (6), (7) мы заменяем ${{w}_{\xi }}$ разностным соотношением и получаем систему обыкновенных дифференциальных уравнений, для которой доказываем теорему существования и затем с помощью предельного перехода доказываем существование решения исходного уравнения.

Для любой функции $f(\xi ,\eta )$ введем обозначение

Уравнения (6) с условиями (7) заменим системой дифференциальных уравнений

с граничными условиями

Доказательство существования решения задачи (6), (7) основано на следующих леммах, доказанных в [14]. Далее через ${{M}_{i}}$ и ${{K}_{i}}$ будем обозначать положительные постоянные, не зависящие от $h$.

Лемма 1. Задача (6), (7) имеет решение ${{w}^{k}}(\eta )$, $k\, = \,0,1, \ldots ,[X{\text{/}}h]$, которое непрерывно при $0 \leqslant \eta \leqslant 1$ и бесконечно дифференцируемо при $0 \leqslant \eta $ < 1, если ${{V}_{x}} > 0$ при $0 \leqslant x \leqslant X$ и V, ${{V}_{x}}$, ${{{v}}_{0}}$ ограничены при $0 \leqslant x \leqslant X$. Для этого решения справедлива оценка

при $kh \leqslant X$, где $h \leqslant {{h}_{0}}$, ${{h}_{0}} = {\text{const}} > 0$, $\mu = {\text{const}}$, $0 < \mu < 1$.

Лемма 2. Задача (8), (9) имеет решение со следующими свойствами:

Замечание 1. Задача (8), (9) является задачей (6), (7) при $k = 0$.

Лемма 3. Предположим, что V(x) = a + $x{{a}_{1}}(x)$, ${{{v}}_{0}}(x) = b + x{{b}_{1}}(x)$, и функции ${{a}_{1}}(x)$, ${{a}_{1}}_{x}(x)$, ${{b}_{1}}(x)$ ограничены при $0 \leqslant x \leqslant X$. Тогда при $0 \leqslant kh \leqslant X$, где X зависит от $V(x)$, ${{{v}}_{0}}(x)$, для решения ${{w}^{k}}(\eta )$ задачи (6), (7) имеют место неравенства

где $Y(\eta )$ – решение задачи (8), (9).

Далее для обоснования предельного перехода в задаче (6), (7) при $h \to 0$ оцениваются величины

равномерно по $h$.

Лемма 4. Пусть выполнены предположения леммы 3; кроме того, ${{a}_{1}}_{{xx}}(x)$ и ${{b}_{1}}_{x}(x)$ ограничены. Тогда при достаточно малом X и ${\kern 1pt} 0 \leqslant kh \leqslant X$ решения ${{w}^{k}}(\eta )$ задачи (6), (7) удовлетворяют неравенствам

где $Y(\eta )$ – решение задачи (8), (9).

Обращая преобразование переменных (3), что возможно в силу свойств решения задачи (4), (5), получаем основной результат о существовании и единственности классического решения задачи (1), (2) в смысле данного нами определения.

4. АСИМПТОТИКИ РЕШЕНИЯ

В этом разделе доказаны теоремы 5 и 6. Задача (1), (2) решена в предположении, что $V(x)$ и ${{{v}}_{0}}(x)$ допускают асимптотическое представление при $x \to 0$ до слагаемых не ниже первого порядка по x. При этом полученные оценки функций $w(\varepsilon ,\eta )$ и ${{u}_{y}}(x,y)$ дают возможность найти главный член асимптотики этих функций при $x \to 0$. Если известны асимптотические при $x \to 0$ разложения функций $V(x)$ и ${{{v}}_{0}}(x)$ с любым числом членов, то возможно получить асимптотическое разложение функции ${{u}_{y}}(x,y)$ до слагаемых любого порядка по $x$ и оценить остаточный член разложения.

Предположим, что имеют место асимптотические разложения (12) и воспользуемся утверждениями из [14].

Лемма 5. Задача для уравнения

с граничными условиями где ${{Y}_{0}}$ – решение задачи (8), (9), имеет решение, удовлетворяющее неравенствамгде ${{N}_{m}}$, ${{C}_{m}}$, ${{R}_{m}}$ – положительные постоянные, $m = 1,\;2,\; \ldots ,\;q$, а $\sigma $ задана формулой (17).

Лемма 6. Пусть имеют место асимптотические разложения (12). Тогда для решения $w(\xi ,\eta )$ задачи (4), (5) справедливы оценки

при $0 \leqslant \xi \leqslant X$, где ${{Y}_{0}}(\eta )$ – решение задачи (8), (9); ${{Y}_{1}}(\eta ),\; \ldots ,\;{{Y}_{q}}(\eta )$ – решение системы (13), с условиями (14); положительные постоянные $X$, ${{C}_{{14}}}$, ${{C}_{{15}}}$ зависят от U(x), ${{{v}}_{0}}(x)$.

Доказательство теоремы 5. Пусть ${{C}_{{16}}} = \max ({{C}_{{14}}},{{C}_{{15}}})$. По лемме 6 имеем

Отсюда легко следует (15). Теорема доказана.

Доказательство теоремы 6. Доказательство теоремы вытекает непосредственно из теоремы 5 и определения функции w.

Из неравенства (16) вытекает, в частности, следующая оценка:

Из (18) вытекает асимптотическое разложение

Поскольку касательная составляющая τ напряжения вязкого трения на поверхности обтекаемого тела равна $\nu \rho {{u}_{y}}(x,0)$, имеем

для любого целого положительного q. Теорема доказана.

5. КОММЕНТАРИИ

Отметим, что результаты работы остаются верными не только для конфузора (тупой угол $\varphi $, см. рис. 1), но и для клина, когда угол $\varphi $ является острым, см. рис. 2.

При этом скорость в пограничном слое в окрестности острия клина имеет степенной характер $U(x) \sim {{x}^{m}}$, где m < 1.