Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 505, № 1, стр. 92-99

ОБ ОПТИМАЛЬНОМ ПОВОРОТЕ ТВЕРДОГО ТЕЛА ПРИ ПОМОЩИ ВНУТРЕННИХ СИЛ

Г. М. Розенблат^1, *

¹ Московский автомобильно-дорожный государственный технический университет (МАДИ)
Москва, Россия

Поступила в редакцию 18.04.2022
После доработки 10.05.2022
Принята к публикации 17.05.2022

EDN: APVBVJ
DOI: 10.31857/S2686954322040154

Аннотация

В статье получен результат, касающийся решения задачи о максимальном повороте твердого тела на заданном интервале времени путем перемещения подвижной внутренней массы. Движения массы реализуются при помощи приложения ограниченной силы. Ранее рассматривались аналогичные задачи, в которых перемещения внутренней массы предполагались кинематическими с ограничениями на скорость точки. Полученный результат описывается аналитическими и легко проверяемыми формулами, оптимальная траектория подвижной массы является спиралью, которая накручивается на центр масс твердого тела с возрастающей до бесконечности частотой.

Ключевые слова: оптимальное управление, принцип максимума Л.С. Понтрягина, динамика твердого тела

1. ВВЕДЕНИЕ

Рассматривается задача о максимальном угле поворота за заданное время плоского твердого тела при помощи ограниченных внутренних сил, реализуемых в процессе движения внутренней точечной массы.

Более точная постановка задачи следующая. Рассматривается плоское твердое тело, которое может совершать плоское движение и на которое не действуют никакие внешние силы. Внутри этого тела имеет возможность двигаться (в плоскости тела при помощи актюаторов) материальная точка. Перемещение точки осуществляется посредством управляющей внутренней силы, которая ограничена по модулю и может быть ориентирована в произвольном направлении в плоскости движения системы. На координаты и скорости точки (относительно твердого тела) не накладываются никакие ограничения (кроме условий дифференцируемости). Требуется выбрать такой допустимый закон изменения управляющей силы, чтобы повернуть тело на максимальный угол за заданное время.

Ранее подобного рода модели (твердое плоское тело, взаимодействующее с подвижной внутренней массой) рассматривались в качестве примеров, иллюстрирующих закон сохранения кинетического момента системы материальных точек (см., например, т. 2, пункт 333 на стр. 38 трактата П. Аппеля [1], учебник Я.В. Татаринова [2], задача 45 на стр. 226). Отметим, однако, что движение подвижной массы (насекомого, по терминологии П. Аппеля из [1]) рассматривалось с кинематической точки зрения, т.е. относительная скорость подвижной массы считалась заданной функцией времени (в частности, постоянной). В учебнике [2] ситуация аналогичная. При формулировке таких задач указывалось, что система “тело+точка” в начальный момент находилась в покое, а затем, в момент t = 0, точка начинала двигаться с некоторой постоянной относительной скоростью ${v}\, = \,{{{v}}_{0}}$. Ясно, что переход точки из состояния ${v} = 0$ в состояние ${v} = {{{v}}_{0}}$ не может произойти мгновенно и реализуется при помощи приложения к точке некоторой ограниченной силы. Это обстоятельство приводит к необходимости определенной коррекции как формулировок, так и полученных в [1, 2] ответов к указанным задачам.

В настоящее время аналогичные модели рассматриваются для исследования управляемых робототехнических устройств, предназначенных для перемещения тел при помощи подвижных внутренних масс (см. работы Ф.Л. Черноусько [3–5], А.М. Шматкова [6]). В этих работах также рассматриваются кинематические перемещения внутренних масс, для которых управлением является вектор скорости, реализующий необходимое оптимальное перемещение объекта (капсюльного робота).

В настоящей работе рассмотренные выше модели применяются для оптимального поворота объекта при помощи подвижной внутренней массы, перемещение которой осуществляется ограниченной по модулю управляющей силой.

2. ОПИСАНИЕ МОДЕЛИ, УРАВНЕНИЯ ДВИЖЕНИЯ И ПОСТАНОВКА ЗАДАЧИ

На рис. 1 изображено сечение твердого тела, центр масс которого находится в точке $C$. $Oxy$ – неподвижная система координат, $C\xi \eta $ – подвижная поступательная система координат, связанная с центром масс тела. Предполагаем, что оси этих систем координат все время параллельны друг другу. Внутри тела находится материальная точка m, которая имеет возможность двигаться посредством приложения внутренней силы F = = ${{({{F}_{x}},{{F}_{y}})}^{T}}$. Для модуля силы F должно соблюдаться следующее ограничение

(2.1)

$F_{x}^{2} + F_{y}^{2} \leqslant F_{0}^{2}.$

Рис. 1.

Тело с движущейся внутренней точечной массой.

Пусть $m$ – масса точки $m$; $M,J$ – масса тела и его момент инерции относительно центра масс C соответственно. Обозначим:

${{x}_{C}},{{y}_{C}}$ – координаты центра масс C тела в системе координат $Oxy$; $\varphi $ – угол поворота тела относительно неподвижной системы координат $Oxy$;

$\xi ,\eta $ – координаты точки m относительно подвижной системы $C\xi \eta $.

Учитывая, что при приложении к подвижной точке m силы F, на тело в той же точке пространства действует сила $F{\kern 1pt} ' = - F$ (согласно третьему закону Ньютона), запишем уравнения движения центра масс и уравнение кинетического момента тела относительно его центра масс.

(2.2)

$M{{\ddot {x}}_{C}} = - {{F}_{x}},\quad M{{\ddot {y}}_{C}} = - {{F}_{y}},\quad J\ddot {\varphi } = \eta {{F}_{x}} - \xi {{F}_{y}}.$

Движение точки m определяется уравнениями второго закона Ньютона.

(2.3)

$m({{\ddot {x}}_{C}} + \ddot {\xi }) = {{F}_{x}},\quad m({{\ddot {y}}_{C}} + \ddot {\eta }) = {{F}_{y}}.$

Из (2.2) и (2.3) получим три уравнения

(2.4)

$\begin{gathered} \ddot {\xi } = \lambda {{F}_{x}},\quad \ddot {\eta } = \lambda {{F}_{y}},\quad \ddot {\varphi } = \mu \left( {\ddot {\xi }\eta - \ddot {\eta }\xi } \right), \\ \lambda = \frac{{M + m}}{{Mm}},\quad \mu = \frac{1}{{\lambda J}}. \\ \end{gathered} $

Далее, для упрощения записи, будем полагать размерности системы единиц такими, что в (2.1) и (2.4) ${{F}_{0}} = 1$, $\lambda = 1,\mu = 1$.

Третье уравнение в системе (2.4) можно проинтегрировать. Предполагая $\dot {\varphi }\left( 0 \right) = 0$, окончательно получаем следующую систему дифференциальных уравнений

$\ddot {\xi } = {{F}_{x}},\quad \ddot {\eta } = {{F}_{y}},\quad \dot {\varphi } = \dot {\xi }\eta - \dot {\eta }\xi + C$

(2.5)

$C = - \dot {\xi }\left( 0 \right)\eta \left( 0 \right) + \xi \left( 0 \right)\dot {\eta }\left( 0 \right).$

В правой части полученного третьего уравнения в системе (2.5) добавлена константа C = = $ - \dot {\xi }(0)\eta (0)\, + \,\xi (0)\dot {\eta }(0)$, чтобы обеспечить выполнение условия $\dot {\varphi }\left( 0 \right) = 0$. Однако нетрудно показать, что эту константу, при решении рассматриваемой оптимальной задачи, можно опустить без ограничения общности.

Систему (2.5) перепишем в стандартной форме системы Коши, вводя обозначения

(2.6)

${{x}_{1}} = \xi ,\quad {{x}_{2}} = \eta ,\quad {{x}_{3}} = \dot {\xi },\quad {{x}_{4}} = \dot {\eta },\quad {{x}_{5}} = \varphi .$

Получаем систему дифференциальных уравнений в стандартной форме

(2.7)

$\begin{gathered} {{{\dot {x}}}_{1}} = {{x}_{3}},\quad {{{\dot {x}}}_{2}} = {{x}_{4}},\quad {{{\dot {x}}}_{3}} = {{F}_{x}},~ \\ {{{\dot {x}}}_{4}} = {{F}_{y}},\quad {{{\dot {x}}}_{5}} = {{x}_{2}}{{x}_{3}} - {{x}_{1}}{{x}_{4}}. \\ \end{gathered} $

Для системы (2.7) ставится следующая задача оптимального управления.

Пусть заданы начальные условия ${{x}_{i}}(0) = {{x}_{{i0}}},$ (i = 1, 5) и время t = T. Требуется определить такой закон изменения управляющих сил ${{F}_{x}},{{F}_{y}}$, которые удовлетворяют ограничениям (2.1), и обеспечивают $\max {{x}_{5}}\left( T \right) = \max \varphi \left( T \right)$.

В классической формулировке задачи Л.С. Понтрягина последнее условие максимума можно заменить следующим

(2.8)

$J = \mathop \smallint \limits_0^T ({{x}_{2}}{{x}_{3}} - {{x}_{1}}{{x}_{4}})dt \to {\text{max}}.$

3. ОСНОВНЫЕ УРАВНЕНИЯ ПРИНЦИПА МАКСИМУМА И ФОРМУЛИРОВКА РЕЗУЛЬТАТА

В настоящем пункте приведены дифференциальные уравнения принципа максимума Л.С. Понтрягина для рассматриваемой оптимальной задачи и излагается полученный результат.

В соответствии с принципом максимума Л.С. Понтрягина [7], вводим сопряженные переменные ${{p}_{k}}\left( {k = 1,5} \right)$, соответствующие фазовым переменным из (2.6), и гамильтониан H для исходной системы дифференциальных уравнений (2.7) по формуле

(3.1)

$H\, = \,{{p}_{1}}{{x}_{3}}\, + \,{{p}_{2}}{{x}_{4}}\, + \,({{p}_{3}}{{F}_{x}}\, + \,{{p}_{4}}{{F}_{y}})\, + \,{{p}_{5}}({{x}_{2}}{{x}_{3}}\, - \,{{x}_{1}}{{x}_{4}}).$

Сопряженные переменные удовлетворяют следующей системе дифференциальных уравнений

${{\dot {p}}_{k}} = - \partial H{\text{/}}\partial {{x}_{k}},\quad ~\left( {k = 1,5} \right).$

В данном случае, используя (3.1), получим уравнения

(3.2)

$\begin{gathered} {{{\dot {p}}}_{1}} = {{p}_{5}}{{x}_{4}},\quad {{{\dot {p}}}_{2}} = - {{p}_{5}}{{x}_{3}}, \\ {{{\dot {p}}}_{3}} = - {{p}_{1}} - {{p}_{5}}{{x}_{2}},\quad {{{\dot {p}}}_{4}} = - {{p}_{2}} + {{p}_{5}}{{x}_{1}},\quad {{{\dot {p}}}_{5}} = 0. \\ \end{gathered} $

Из последнего уравнения системы (3.2) следует, что ${{p}_{5}} = {\text{const}} \geqslant 0$. Тогда система (3.2) приобретает следующий вид

(3.3)

Согласно принципу максимума оптимальное управление F доставляет максимум функции H из (3.1), и при ограничениях (2.1) имеет вид

(3.4)

${{F}_{x}} = \frac{{{{p}_{3}}}}{{\sqrt {p_{3}^{2} + p_{4}^{2}} }},\quad {{F}_{y}} = \frac{{{{p}_{4}}}}{{\sqrt {p_{3}^{2} + p_{4}^{2}} }}.$

Кроме того, так как на конечные значения x_k(T), $(k = 1,4)$ не наложено никаких ограничений, должны быть выполнены условия трансверсальности

(3.5)

${{p}_{k}}\left( T \right) = 0,{\text{\;\;}}\left( {k = 1,4} \right).$

Дифференцируя дважды последние два уравнения системы (3.3) и используя (2.7) и (3.4), получим следующие два уравнения для двух сопряженных переменных ${{p}_{3}},~{{p}_{4}}$:

(3.6)

$\begin{gathered} {{{\dddot p}}_{3}} = - \lambda \frac{{{{p}_{4}}}}{{\sqrt {p_{3}^{2} + p_{4}^{2}} }},\quad {{{\dddot p}}_{4}} = \lambda \frac{{{{p}_{3}}}}{{\sqrt {p_{3}^{2} + p_{4}^{2}} }}, \\ \lambda = 2{{p}_{5}} = {\text{const}} \geqslant 0. \\ \end{gathered} $

Таким образом, задача сводится к поиску решений системы 6-го порядка (3.6) на отрезке $0 \leqslant t \leqslant T$, которые удовлетворяют краевым условиям

(3.7)

${{p}_{3}}\left( T \right) = {{p}_{4}}\left( T \right) = 0.$

Мы можем понизить на две единицы порядок системы (3.6), записав следующие два ее интеграла

(3.8)

$\begin{gathered} {{p}_{3}}{{{\ddot {p}}}_{3}} + {{p}_{4}}{{{\ddot {p}}}_{4}} = \frac{1}{2}(\dot {p}_{3}^{2} + \dot {p}_{4}^{2}) + {{C}_{1}}, \\ {\text{\;}} - {{{\dot {p}}}_{4}}{{{\ddot {p}}}_{3}} + {{{\dot {p}}}_{3}}{{{\ddot {p}}}_{4}} = \lambda \sqrt {p_{3}^{2} + p_{4}^{2}} + {{C}_{2}}, \\ \end{gathered} $

где ${{C}_{1}},{{C}_{2}}$ – произвольные постоянные, определяемые начальными и конечными условиями для переменных ${{p}_{3}},{{p}_{4}}$. Система (3.8) является уже системой 4-го порядка. Можно еще понизить порядок системы (3.8) на две единицы при помощи следующих замен

(3.9)

$\begin{gathered} {{p}_{3}} = \rho \cos \alpha ,\quad {{p}_{4}} = \rho \sin \alpha , \\ {{{\dot {p}}}_{3}} = {v}\cos \beta ,\quad {{{\dot {p}}}_{4}} = {v}\sin \beta . \\ \end{gathered} $

Из (3.8) и (3.9), обозначая $\gamma = \beta - \alpha $, получаем следующие 4 уравнения первого порядка

$\dot {\rho } = {v}\cos \gamma ,~\quad \rho \dot {\alpha } = {v}\sin \gamma ,~$

(3.10)

$\begin{gathered} \rho {\dot {v}}\cos \gamma - \rho {v}\dot {\beta }\sin \gamma = \frac{1}{2}{{{v}}^{2}} + {{C}_{1}}, \\ ~{{{v}}^{2}}\dot {\beta } = \lambda \rho + {{C}_{2}},\quad \left( {\gamma = \beta - \alpha } \right). \\ \end{gathered} $

Отсюда получаем замкнутую систему трех дифференциальных уравнений первого порядка относительно трех функций $\left\{ {\rho ,{v},\gamma } \right\}$ (уравнение для $\beta $ “отщепляется”):

$\dot {\rho } = {v}\cos \gamma ,~\quad {v}\rho \dot {\gamma } = - {{{v}}^{2}}\sin \gamma + \frac{{\rho \left( {\lambda \rho + {{C}_{2}}} \right)}}{{v}},~$

(3.11)

$\begin{gathered} {\dot {v}}\rho \cos \gamma = \frac{{\rho \left( {\lambda \rho + {{C}_{2}}} \right)}}{{v}}\sin \gamma + \frac{{{{{v}}^{2}}}}{2} + {{C}_{1}}, \\ ~\left( {\sin \gamma \ne 0} \right). \\ \end{gathered} $

Если в системе (3.11) поделить второе и третье уравнения на первое и взять за независимое переменное функцию ρ, то получим систему второго порядка для двух переменных $\left( {{v},\gamma } \right)$.

Таким образом, нам нужно найти такие решения системы (3.11) на отрезке $0 \leqslant t \leqslant T$, которые удовлетворяют краевому условию $\rho \left( T \right) = 0$, чтобы обеспечить условие трансверсальности (3.7). Аналитически эти решения удалось найти лишь в том частном случае, когда ${{C}_{1}} = {{C}_{2}} = 0$. Справедливо следующее утверждение.

Утверждение 1. Система (3.11) в случае ${{C}_{1}} = {{C}_{2}} = 0$ имеет частное решение, которое дается соотношениями

(3.12)

$\begin{gathered} \gamma \left( t \right) = {{\gamma }_{0}} = \pm \arcsin (1{\text{/}}\sqrt {10} ) = {\text{const,}}~~ \\ {v}\left( t \right) = {{( \pm \sqrt {10} \lambda )}^{{1/3}}}{{\left[ {\rho \left( t \right)} \right]}^{{2/3}}}. \\ \end{gathered} $

Справедливость утверждения 1 устанавливается непосредственной проверкой.

Далее, используя первые два уравнения системы (3.11) и соотношения (3.12), получим искомые решения системы (3.6) как функции времени на отрезке $0 \leqslant t \leqslant T$:

${{p}_{3}}\left( t \right) = {{p}_{*}}{{(1 - \tau )}^{3}}\cos \left[ {{{\alpha }_{0}} + \ln (1 - \tau )} \right],$

(3.13)

$\begin{gathered} {{p}_{4}}\left( t \right) = - {{p}_{*}}{{(1 - \tau )}^{3}}\sin \left[ {{{\alpha }_{0}} + \ln (1 - \tau )} \right], \\ ~{{p}_{*}}\, = \,\lambda {{T}^{3}}{\text{/}}10,~\quad \tau \, = \,t{\text{/}}T,~ \\ {{\alpha }_{0}}\, = \,{\text{const}},\quad \tau \, \in \,[0,1]. \\ \end{gathered} $

Используя формулы (3.6) и (3.13), получаем выражения для оптимальных управлений

${{F}_{x}} = \cos \left[ {{{\alpha }_{0}} + \ln (1 - \tau )} \right],$

(3.14)

$\begin{gathered} {{F}_{y}} = - \sin \left[ {{{\alpha }_{0}} + \ln (1 - \tau )} \right],{\text{\;}} \\ \tau = t{\text{/}}T,\quad {{\alpha }_{0}} = {\text{const}} \in \left[ {0,2\pi } \right),\quad \tau \in \left[ {0,1} \right]. \\ \end{gathered} $

Подставляя функции из (3.14) в уравнения движения (2.7), находим соответствующие оптимальные траектории точки в системе координат $C\xi \eta $ и максимальный угол поворота тела. Несложно получить, что эти траектории представляют собой спирали, закручивающиеся вокруг центра масс C бесконечное число раз. В конце этого процесса, при $t \to T$, направление управляющей силы $F$меняется с увеличивающейся до бесконечности частотой.

В формулах (3.14) α₀ – произвольная константа из интервала [0, 2π]. Используя (3.14), мы можем решить полную систему уравнений (2.7), (3.3) на отрезке $0 \leqslant t \leqslant T$ и определить все те начальные условия ${{x}_{k}}\left( 0 \right) = {{x}_{{k0}}},~\left( {k = 1,4} \right)$, при которых соблюдены условия трансверсальности p_k(T) = 0, $(k = 1,4)$. Проводя элементарные выкладки, мы получаем следующий результат.

Утверждение 2. Если начальные условия в рассматриваемой задаче удовлетворяют следующим параметрическим соотношениям

$\begin{gathered} ~~{{x}_{{10}}} = \xi \left( 0 \right) = \frac{{{{T}^{2}}}}{{10}}\left( {\cos {{\alpha }_{0}} + 3\sin {{\alpha }_{0}}} \right), \\ ~{{x}_{{20}}} = \eta \left( 0 \right) = \frac{{{{T}^{2}}}}{{10}}\left( {3\cos {{\alpha }_{0}} - \sin {{\alpha }_{0}}} \right), \\ \end{gathered} $

(3.15)

$\begin{gathered} {{x}_{{30}}} = \dot {\xi }\left( 0 \right) = - \frac{T}{2}\left( {\cos {{\alpha }_{0}} + \sin {{\alpha }_{0}}} \right), \\ ~{{x}_{{40}}} = \dot {\eta }\left( 0 \right) = \frac{T}{2}\left( { - \cos {{\alpha }_{0}} + \sin {{\alpha }_{0}}} \right), \\ {{\alpha }_{0}} \in \left[ {0,2\pi } \right], \\ \end{gathered} $

то при управляющих силах из (3.14) тело за время T повернется на максимальный угол. При этом оптимальные траектории спиралеобразно стремятся к точке

$\xi \left( T \right) = \dot {\xi }\left( T \right) = \eta \left( T \right) = \dot {\eta }\left( T \right) = 0.$

Справедливость утверждения 2 следует из принципа максимума Понтрягина и непосредственного интегрирования системы уравнений (2.7), (3.3) при функциях ${{F}_{x}},{{F}_{y}}$, вычисляемых по формулам (3.14).

Замечание 1. В силу однородности пространства в формулах (3.15) можно принять ${{\alpha }_{0}} = 0$. Тогда искомые начальные условия будут такими

$\begin{gathered} {{x}_{{10}}} = \xi \left( 0 \right) = \frac{{{{T}^{2}}}}{{10}},\quad {{x}_{{20}}} = \eta \left( 0 \right) = \frac{{3{{T}^{2}}}}{{10}}, \\ {{x}_{{30}}} = \dot {\xi }\left( 0 \right) = - \frac{T}{2},~\quad {{x}_{{40}}} = \dot {\eta }\left( 0 \right) = - \frac{T}{2}. \\ \end{gathered} $

Оптимальное управление из (3.14) примет вид

$\begin{gathered} {{F}_{x}} = \cos \left[ {\ln (1 - s)} \right],\quad {{F}_{y}} = - \sin \left[ {\ln (1 - s)} \right], \\ s = t{\text{/}}T,\quad ~t \in \left[ {0,T} \right]. \\ \end{gathered} $

Решая систему (2.5) при указанных начальных условиях и управлениях ${{F}_{x}},{{F}_{y}}$, получим следующие формулы для координат и скоростей

$\begin{gathered} {{x}_{1}}\left( t \right) = \xi \left( t \right) = \frac{{{{T}^{2}}}}{{\sqrt {10} }}{{\tau }^{2}}\sin ({{\gamma }_{0}} + \ln \tau ),~ \\ {{x}_{2}}\left( t \right) = \eta \left( t \right) = \frac{{{{T}^{2}}}}{{\sqrt {10} }}{{\tau }^{2}}\cos ({{\gamma }_{0}} + \ln \tau ), \\ \end{gathered} $

$\begin{gathered} {{x}_{3}}\left( t \right) = \dot {\xi }\left( t \right) = - \frac{T}{{\sqrt 2 }}\tau \sin \left( {\frac{\pi }{4} + \ln \tau } \right), \\ {{x}_{4}}\left( t \right) = \dot {\eta }\left( t \right) = - \frac{T}{{\sqrt 2 }}\tau \cos \left( {\frac{\pi }{4} + \ln \tau } \right), \\ \end{gathered} $

$\begin{gathered} {{{\dot {x}}}_{5}}\left( t \right) = \dot {\varphi }\left( t \right) = - \frac{{{{T}^{3}}}}{{10}}(1 - {{\tau }^{3}}),{\text{\;\;}} \\ {{x}_{5}}\left( t \right) = \varphi \left( t \right) = \frac{{{{T}^{4}}}}{{10}}\left( {\frac{3}{4} - \tau + \frac{{{{\tau }^{4}}}}{4}} \right),~ \\ \end{gathered} $

(3.16)

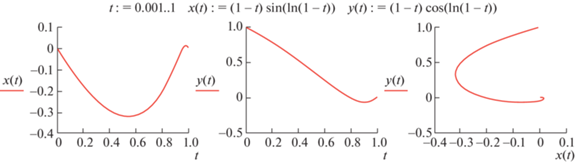
$\begin{gathered} {\text{sin}}{{\gamma }_{0}} = \frac{1}{{\sqrt {10} }},\quad \cos {{\gamma }_{0}} = \frac{3}{{\sqrt {10} }},~ \\ \tau = 1 - \frac{t}{T},~\quad t \in \left[ {0,T} \right]. \\ \end{gathered} $

Из (3.16) следует, что оптимальный угол поворота равен ${{x}_{5}}\left( T \right) = \varphi \left( T \right) = \frac{{3{{T}^{4}}}}{{40}}$, траектории точки по координатам и скоростям приближаются спиралеобразно в точку нуль. На рис. 2, 3 представлены графики траекторий точки, соответственно, по координатам и скоростям.

Рис. 2.

Оптимальные траектории точки по координатам.

Рис. 3.

Оптимальные траектории точки по скоростям.

4. РЕШЕНИЕ ОПТИМАЛЬНОЙ ЗАДАЧИ МЕТОДОМ ПОЛЯРНЫХ КООРДИНАТ

В предыдущем пункте решение задачи Л.С. Понтрягина осуществлялось в декартовых координатах. В настоящем пункте исходная задача оптимального управления решается с использованием полярных координат. Такой метод позволяет сократить выкладки и лучше прояснить механический смысл полученных результатов.

В системе (2.7) перейдем к полярным переменным по формулам

(4.1)

$\begin{gathered} {{x}_{1}} = \rho \cos \alpha ,\quad {{x}_{2}} = \rho \sin \alpha , \\ {{x}_{3}} = {v}\cos \beta ,\quad {{x}_{4}} = {v}\sin \beta . \\ \end{gathered} $

Тогда система (2.7) примет вид

(4.2)

$\begin{gathered} \dot {\rho } = {v}\cos \gamma ,\quad \rho \dot {\alpha } = - {v}\sin \gamma , \\ ~{\dot {v}} = {{F}_{{v}}},\quad ~{v}\dot {\beta } = {{F}_{\beta }},\quad \dot {\varphi } = \rho {v}\sin \gamma . \\ \end{gathered} $

В (4.2) приняты следующие обозначения

(4.3)

$\begin{gathered} {{F}_{{v}}} = {{F}_{x}}\cos \beta + {{F}_{y}}\sin \beta ,~ \\ {{F}_{\beta }} = - {{F}_{x}}\sin \beta + {{F}_{y}}\cos \beta ,~\quad \gamma = \alpha - \beta . \\ \end{gathered} $

Согласно (4.3), ${{F}_{{v}}},{{F}_{\beta }}$ суть проекции управляющей силы F на оси скоростной системы координат (касательную и нормаль, соответственно, к траектории точки в декартовой системе координат $~C\xi \eta $). Ясно, что эти проекции также удовлетворяют ограничению

(4.4)

$F_{{v}}^{2} + F_{\beta }^{2} \leqslant F_{0}^{2} = 1.$

Путем несложных преобразований можно сократить число уравнений в системе (4.2). В результате получаем следующую систему четырех дифференциальных уравнений для четырех переменных $\left\{ {\rho ,\gamma ,{v},\varphi } \right\}$

(4.5)

$\begin{gathered} \dot {\rho } = {v}\cos \gamma ,~\quad \dot {\gamma } = - \frac{{v}}{\rho }\sin \gamma - \frac{1}{{v}}{{F}_{\beta }},\quad {\dot {v}} = {{F}_{{v}}},~ \\ \dot {\varphi } = \rho {v}\sin \gamma ,~\quad t \in \left[ {0,T} \right]. \\ \end{gathered} $

Для системы (4.5) ставится аналогичная пункту 2 оптимальная задача. Найти функции ${{F}_{{v}}},{{F}_{\beta }}$, которые при ограничениях (4.4) и заданных начальных условиях $\left\{ {\rho (0),\gamma (0),{v}(0),\varphi (0) = 0} \right\}~$ обеспечивают для решения системы (4.5) $\max \varphi \left( T \right)$.

Используя принцип максимума Л.С. Понтрягина, вводим сопряженные переменные $\{ {{p}_{1}},{{p}_{2}},{{p}_{3}},{{p}_{4}}\} $, которые соответствуют исходным переменным $\left\{ {\rho ,\gamma ,{v},\varphi } \right\}$ в написанном порядке. Далее составляем гамильтониан, который запишем в следующем виде

(4.6)

$\begin{gathered} H = {v}\left( {{{p}_{1}}\cos \gamma - \frac{{{{p}_{2}}}}{\rho }\sin \gamma + {{p}_{4}}\rho \sin \gamma } \right) + \\ + \left( { - \frac{{{{p}_{2}}}}{{v}}{{F}_{\beta }} + {{p}_{3}}{{F}_{{v}}}} \right). \\ \end{gathered} $

В соответствии с принципом максимума оптимальные функции ${{F}_{{v}}},{{F}_{\beta }}$ реализуют максимум функции H из (4.6), и при ограничениях (4.4) имеют вид

(4.7)

$\begin{gathered} {{F}_{\beta }} = - {{p}_{2}}{\text{/}}{{p}_{0}},\quad {{F}_{{v}}} = q{\text{/}}{{p}_{0}}, \\ {\text{где\;обозначено\;}}q = {v}{{p}_{3}},\quad {{p}_{0}} = \sqrt {p_{2}^{2} + {{q}^{2}}} . \\ \end{gathered} $

Из дифференциальных уравнений для сопряженных переменных следует, что ${{\dot {p}}_{4}} = 0$, т.е. p₄ = λ = = ${\text{const}} \geqslant 0$. Записывая уравнения для других сопряженных переменных, присоединяя к ним динамические уравнения (4.5) и используя равенства (4.7), получаем следующую систему шести дифференциальных уравнений для шести функций $\left\{ {\rho ,\gamma ,{v},{{p}_{1}},{{p}_{2}},{{p}_{3}}} \right\}$

$\dot {\rho } = {v}\cos \gamma ,\quad \dot {\gamma } = - \frac{{v}}{\rho }\sin \gamma + \frac{{{{p}_{2}}}}{{{v}{{p}_{0}}}},\quad {\dot {v}} = \frac{q}{{{{p}_{0}}}},$

$\begin{gathered} {{{\dot {p}}}_{1}} = - \left( {\frac{{{{p}_{2}}}}{{{{\rho }^{2}}}} + \lambda } \right){v}\sin \gamma ,~ \\ {{{\dot {p}}}_{2}} = {v}\left[ {{{p}_{1}}\sin \gamma + \left( {\frac{{{{p}_{2}}}}{\rho } - \lambda \rho } \right)\cos \gamma } \right], \\ \end{gathered} $

(4.8)

$\begin{gathered} {{{\dot {p}}}_{3}} = - {{p}_{1}}\cos \gamma + \left( {\frac{{{{p}_{2}}}}{\rho } - \lambda \rho } \right)\sin \gamma + \frac{{p_{2}^{2}}}{{{{{v}}^{2}}{{p}_{0}}}}, \\ t \in \left[ {0,T} \right]. \\ \end{gathered} $

В системе (4.8) приняты обозначения из (4.7). Кроме того, так как на исходные переменные ρ(t), $\gamma (t),{v}(t)$ при t = T не наложено никаких ограничений, то должны быть выполнены условия трансверсальности

(4.9)

${{p}_{1}}\left( T \right) = {{p}_{2}}\left( T \right) = {{p}_{3}}\left( T \right) = 0.$

Таким образом, требуется решить систему дифференциальных уравнений (4.8) на отрезке $0 \leqslant t \leqslant T$ при заданных начальных условиях для переменных $\left\{ {\rho ,\gamma ,{v}} \right\}$ и условиях трансверсальности (4.9) для переменных $\left\{ {{{p}_{1}},{{p}_{2}},{{p}_{3}}} \right\}$. Для некоторых начальных условий это удалось сделать аналитически.

Перейдем в системе (4.8) к независимой переменной $\rho $. Для этого поделим обе части всех уравнений, начиная со второго, на первое уравнение. Получим систему пяти уравнений для пяти переменных $\left\{ {\gamma ,{v},{{p}_{1}},{{p}_{2}},{{p}_{3}}} \right\}$ (производная по $\rho $ обозначается штрихом)

$\gamma {\kern 1pt} ' = - \frac{{{\text{tg}}\gamma }}{\rho } + \frac{{{{p}_{2}}}}{{{{{v}}^{2}}{{p}_{0}}\cos \gamma }},\quad {v}{\kern 1pt} ' = \frac{q}{{{v}{{p}_{0}}\cos \gamma }},$

$p_{1}^{'} = - \left( {\frac{{{{p}_{2}}}}{{{{\rho }^{2}}}} + \lambda } \right){\text{tg}}\gamma ,\quad p_{2}^{'} = {{p}_{1}}{\text{tg}}\gamma + \frac{{{{p}_{2}}}}{\rho } - \lambda \rho ,$

(4.10)

$p_{3}^{'} = - \frac{1}{{v}}\left[ {{{p}_{1}} - \left( {\frac{{{{p}_{2}}}}{\rho } - \lambda \rho } \right){\text{tg}}\gamma } \right] + \frac{{p_{2}^{2}}}{{{{{v}}^{3}}{{p}_{0}}\cos \gamma }}.$

Система (4.10) имеет два интеграла

(4.11)

$p_{1}^{2} + {{\left( {\frac{{{{p}_{2}}}}{\rho } + \lambda \rho } \right)}^{2}} = {{h}^{2}} = {\text{const,}}$

(4.12)

$\begin{gathered} {v}\left( {{{p}_{1}}{\text{cos}}\gamma \, - \,\frac{{{{p}_{2}}}}{\rho }{\text{sin}}\gamma \, + \,\lambda \rho {\text{sin}}\gamma } \right)\, + \,\frac{{{{p}_{0}}}}{{v}}\, = \,H\, = \,{\text{const}},~ \\ {{p}_{0}} = \sqrt {p_{2}^{2} + q} ,\quad ~q = {v}{{p}_{3}}. \\ \end{gathered} $

Интеграл (4.11) получается непосредственно из третьего и четвертого уравнений системы (4.10). Интеграл (4.12) следует из сохранения значения функции Гамильтона (4.6) при значениях ${{F}_{{v}}},{{F}_{\beta }}$ из (4.7) в силу уравнений (4.8). Константы h, H в (4.11) и (4.12) определяются заданными начальными условиями для $\left\{ {\rho ,\gamma ,{v}} \right\}$ и условиями трансверсальности (4.9).

Благодаря интегралу (4.11), можно понизить порядок системы (4.10). Введем вместо ${{p}_{1}},{{p}_{2}}$ новую переменную σ по формулам

(4.13)

${{p}_{1}}\, = \,h{\text{sin}}\sigma ,\quad {{p}_{2}}\, = \,\rho \left( {h{\text{cos}}\sigma - \lambda \rho } \right),\quad ~\sigma \, \in \,[0,2\pi ].$

Тогда интеграл (4.11) соблюдается автоматически, а система (4.10) будет эквивалентна следующим четырем уравнениям для четырех переменных $\left\{ {\gamma ,~\sigma ,~{v},~q} \right\},~\left( {q = {v}{{p}_{3}}} \right)$

$\gamma {\kern 1pt} ' = - \frac{{{\text{tg}}\gamma }}{\rho } + \frac{{{{p}_{2}}}}{{{{{v}}^{2}}{{p}_{0}}\cos \gamma }},\quad {v}{\kern 1pt} ' = \frac{q}{{{v}{{p}_{0}}\cos \gamma }},$

(4.14)

$\sigma {\kern 1pt} ' = - \frac{{{\text{tg}}\gamma }}{\rho },\quad q{\kern 1pt} ' = - {{p}_{1}}\, + \,\left( {\frac{{{{p}_{2}}}}{\rho } - \lambda \rho } \right){\text{tg}}\gamma \, + \,\frac{{{{p}_{0}}}}{{{{{v}}^{2}}{\text{cos}}\gamma }}.$

В уравнениях (4.14) ${{p}_{1}},{{p}_{2}}$ даются формулами (4.13), а p₀, q определяются обозначениями из (4.7).

Введем новую переменную p по формуле

(4.15)

$q = {v}{{p}_{3}} = p{{p}_{2}} = p\rho \left( {h\cos \sigma - \lambda \rho } \right).$

Тогда имеем ${{p}_{0}} = \left| {{{p}_{2}}} \right|\sqrt {1 + {{p}^{2}}} $, и система уравнений (4.14) примет вид

$\begin{gathered} \gamma ' = - \frac{{{\text{tg}}\gamma }}{\rho } + \frac{{\operatorname{sgn} {{p}_{2}}}}{{{{{v}}^{2}}\cos \gamma \sqrt {1 + {{p}^{2}}} }}, \\ {v}' = \frac{{p\operatorname{sgn} {{p}_{2}}}}{{{v}\cos \gamma \sqrt {1 + {{p}^{2}}} }},\quad \sigma ' = - \frac{{{\text{tg}}\gamma }}{\rho }, \\ \end{gathered} $

(4.16)

$\begin{gathered} ~{{p}_{2}}p' = - h\sin \sigma - ph\sin \sigma {\text{tg}}\gamma + \\ + \left( {h\cos \sigma - 2\lambda \rho } \right)\left( {{\text{tg}}\gamma - p} \right) + \frac{{\left| {{{p}_{2}}} \right|\sqrt {1 + {{p}^{2}}} }}{{{{{v}}^{2}}\cos \gamma }}. \\ \end{gathered} $

Рассмотрим такие начальные условия, для которых h = 0. В этом случае из интеграла (4.11) следует, что

(4.17)

${{p}_{1}} \equiv 0,\quad {{p}_{2}} = - \lambda {{\rho }^{2}}.$

Уравнения (4.16) приобретают вид

$\begin{gathered} \gamma ' = - \frac{{{\text{tg}}\gamma }}{\rho } - \frac{1}{{{{{v}}^{2}}\cos \gamma \sqrt {1 + {{p}^{2}}} }},{\text{\;\;}} \\ {v}' = - \frac{p}{{{v}\cos \gamma \sqrt {1 + {{p}^{2}}} }},~ \\ \end{gathered} $

(4.18)

$ - \lambda {{\rho }^{2}}p' = \left( { - 2\lambda \rho } \right)\left( {{\text{tg}}\gamma - p} \right) + \frac{{\lambda {{\rho }^{2}}\sqrt {1 + {{p}^{2}}} }}{{{{{v}}^{2}}\cos \gamma }}.$

Далее полагаем $u = {{{v}}^{2}}$. Тогда система (4.18) примет вид

(4.19)

$\begin{gathered} \gamma '\, = \, - {\kern 1pt} \frac{{{\text{tg}}\gamma }}{\rho }\, - \,\frac{1}{{u{\text{cos}}\gamma \sqrt {1\, + \,{{p}^{2}}} }},\quad u'\, = \, - {\kern 1pt} \frac{{2p}}{{{\text{cos}}\gamma \sqrt {1\, + \,{{p}^{2}}} }},{\text{\;}} \\ p' = \frac{2}{\rho }\left( {{\text{tg}}\gamma - p} \right) - \frac{{\sqrt {1 + {{p}^{2}}} }}{{u\cos \gamma }}. \\ \end{gathered} $

Из формулы (4.12) для рассматриваемых начальных условий получим следующий интеграл системы (4.19)

(4.20)

$2\rho \sqrt u \sin \gamma + \frac{{{{\rho }^{2}}}}{{\sqrt u }}\sqrt {1 + {{p}^{2}}} = H = {\text{const}}.$

Уравнения (4.19) имеют стационарные решения $\gamma = {{\gamma }_{0}},p = {{p}_{0}},~u = {{{v}}^{2}} = k\rho ,~(k > 0)$, для которых выполнены соотношения

(4.21)

$\begin{gathered} {\text{tg}}{{\gamma }_{0}} = \pm 1{\text{/}}2,\quad {{p}_{0}} = \pm 1,~ \\ k = - \frac{{2{{p}_{0}}}}{{(\sqrt {1 + p_{0}^{2}} )\cos {{\gamma }_{0}}}},\quad {v} = \sqrt {k\rho } . \\ \end{gathered} $

Эти решения удовлетворяют также интегралу (4.20) при H = 0. Так как $k > 0$, то из (4.21) получим

(4.22)

$\begin{gathered} p = {{p}_{0}} = \pm 1,\quad {\text{tg}}\gamma = {\text{tg}}{{\gamma }_{0}} = \pm 1{\text{/}}2,~ \\ {\text{cos}}{{\gamma }_{0}}\, = \, \mp {\kern 1pt} 2{\text{/}}\sqrt 5 ,\quad {\text{sin}}{{\gamma }_{0}}\, = \, - {\kern 1pt} 1{\text{/}}\sqrt 5 ,\quad k\, = \,\sqrt {10} {\text{/}}2. \\ \end{gathered} $

Отметим, что в силу условий трансверсальности (4.9), формул (4.17) и обозначений (4.15), имеем $\rho \left( T \right) = 0,~\,\,{v}\left( T \right) = \sqrt {k\rho \left( T \right)} = 0$. В результате приходим к решениям, полученным в пункте 2.

Замечание 2. Нетрудно установить, используя (4.7), (4.15) и первое равенство из (4.22), что оптимальная сила F удовлетворяет соотношениям $\left| {{{F}_{{v}}}} \right| = \left| {{{F}_{\beta }}} \right| = \sqrt 2 {\text{/}}2$. Таким образом, сила F является постоянной по модулю (равным единице) и всегда направлена под углом 45° к касательной траектории подвижной точки в системе $C\xi \eta $. Эта сила является “следящей” по скорости точки. Отметим, что в монографии В.Ф. Журавлёва и Д.М. Климова [8] (см. пункт 3.5.2 на стр. 115) рассматривалась задача о “следящей” силе по позиции точки (сила была также постоянна по модулю и всегда перпендикулярна радиусу-вектору точки). Спиралеобразные траектории движения точки, полученные в монографии [8], вполне аналогичны траекториям в настоящей работе.

Замечание 3. В работе [9] численно исследовалась задача об оптимальной раскрутке плоской двухмассовой системы, где управлением являлся ограниченный внешний момент, приложенный к одному из тел.

Замечание 4. Аналитические выражения для оптимальных траекторий в рассматриваемой задаче удалось получить лишь для достаточно узкого класса начальных условий. При этом оказалось, что оптимальные траектории подвижной массы в конце интервала управления по спиралям приходят с нулевой предельной скоростью в центр масс тела. Весьма вероятно, что аналогичный эффект будет наблюдаться и для других начальных условий. Однако для доказательства этого факта потребуются дополнительные численно-аналитические исследования решений приведенных в статье дифференциальных уравнений.

Замечание 5. При исследовании, редукции и поиске первых интегралов дифференциальных уравнений настоящей статьи использовались идеи и методы, которые были развиты в работах [10, 11].

БЛАГОДАРНОСТИ

Автор выражает свою благодарность академику РАН В.Ф. Журавлёву за поддержку и внимание к работе, а также академику РАН Ф.Л. Черноусько и всем участникам руководимого им семинара за ценные и конструктивные замечания к настоящей работе.

Список литературы

Аппель П. Теоретическая механика. Т. 2: Динамика системы. Аналитическая механика. Пер. с фр. / Под науч. ред. С.М. Тарга. Предисл. В.Ф. Журавлёва и Г.М. Розенблата. Изд. 2-е, дополн. М.: ЛЕНАНД, 2021. 504 с.
Татаринов Я.В. Лекции по классической динамике. М.: Изд-во Моск. ун-та, 1984. 296 с.
Chernousko F.L. Optimal Control of Two-Dimensional Motions of a Body by a Movable Mass. Preprints of the IX Vienna Intern. Conf. on Mathematical Modelling (MATHMOD). Vienna, February 21–23, 2018. Pap. WeD4.2. Vienna, 2018. P. 253–256.
Черноусько Ф.Л. Оптимальное управление движением двухмассовой системы // Доклады Академии наук. 2018. Т. 480. № 5. С. 528–532.
Черноусько Ф.Л. Изменение ориентации твердого тела при помощи вспомогательной массы // Доклады Российской академии наук. Физика. Технические науки. 2020. Т. 490. С. 79–81.
Шматков А.М. Поворот тела за кратчайшее время перемещением точечной массы // Доклады Академии наук. 2018. Т. 481. № 5. С. 498–502.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: 1961. Государственное издательство физико-математической литературы. 391 с.
Klimov D.M. and Zhuravlev V.Ph. Group-Theoretic Methods in Mechanics and Applied Mathematics. Taylor & Francis. 2002. 230 p.
Решмин С.А. Применение метода Ньютона при решении краевых задач принципа максимума на примере задачи об оптимальном раскручивании двухмассовой системы // Modern European Researches. 2021. V. 1. № 2. P. 114–122.
Козлов В.В. Рациональные интегралы квазиоднородных динамических систем.// Прикл. матем. и механ. 2015. Т. 79. № 3. С. 307–316.
Шамолин М.В. Новые случаи интегрируемых систем нечетного порядка с диссипацией // Доклады РАН. Математика, информатика, процессы управления. 2020. Т. 491. № 1. С. 95–101.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал