Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 505, № 1, стр. 24-29

Математические модели, описывающие распространение эпидемии COVID-19, начали разрабатываться практически одновременно с первой вспышкой заболевания в Китае в январе 2020 г. В основе таких моделей лежат различные подходы, обзоры которых содержатся, например, в работах [1–3]. Существенным недостатком большинства разработанных математических моделей является их неспособность имитировать циклические процессы, которые характерны для волнообразной динамики заболеваемости коронавирусом. Наконец, отсутствуют модели, которые генерируют конкретные математически обоснованные размеры и сроки осуществления мероприятий по преодолению пандемии и направленных на обеспечение экономического роста.

Данная работа посвящена математическому моделированию процессов преодоления пандемии и восстановления экономического роста, а также моделированию необходимых объемов антикризисных мер и эффективных сроков их проведения. В качестве базовых экономико-математических моделей были использованы модель Кермака–Маккендрика [4] и модель Сандерсона [5, 6].

Предложенная В. Кермаком и А. Маккендриком [4] модель является классической SIR-моделью распространения инфекции и состоит из 3 дифференциальных уравнений. Отдельные эксперты считают ошибочным использование SIR-моделей для описания пандемии коронавируса [7]. Действительно, в этой модели считается, что переболевшие индивиды приобретают иммунитет и не могут быть заражены вторично. Для пандемии COVID-19 это предположение не выполняется. Более того, в SIR-модели не учитывается процесс вакцинации от вирусной инфекции. В этой связи мы добавили в SIR-модель четвертое “вакцинное” уравнение и ввели поправочные компоненты, которые учитывают возможность повторного заражения и другие нюансы. Кроме того, поскольку при практическом моделировании приходится оперировать дискретными значениями статистики, то целесообразен переход от дифференциальных уравнений к разностным уравнениям. В результате мы получили эпидемо-математическую модель в виде дискретной системы уравнений:

Здесь S_j, I_j, R_j, V_j – соответственно численности восприимчивых к заражению (не болевших COVID, но и не сделавших вакцинацию), больных COVID, выздоровевших, полностью вакцинированных (двумя дозами) граждан; r − коэффициент скорости заражения COVID; ν − коэффициент интенсивности выздоровления инфицированных индивидов; q и b – коэффициенты вакцинации соответственно для не болевших и переболевших COVID; d − коэффициент ревакцинации; с − коэффициент повторного заражения COVID; a − коэффициент флуктуации населения, который учитывает эффект изменения численности населения в результате рождаемости и смертности и в силу миграции граждан.

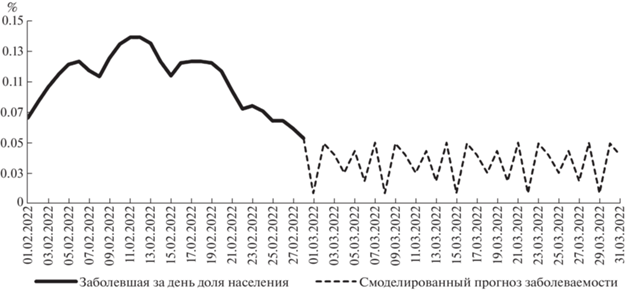
В качестве примера рассмотрим коронавирусную статистику по России [8]. Высший пик заболеваемости пришелся на февраль 2022 г., причем динамика заболеваемости имела “пилообразную” конфигурацию. Рисунок 1 содержит ежедневные показатели новых заражений коронавирусом среди граждан России в феврале. Динамика заболеваемости имеет четко прослеживаемую цикличность с периодом 7 дней.

Покажем, что модель (1) позволяет генерировать циклические траектории с требуемой периодичностью. Из выше изложенного следует, что интерес представляют циклы с периодом 7 дней. В результате компьютерного эксперимента были подобраны численные значения параметров системы (1):

C помощью приближенных методов были найдены начальные условия, при которых система (1) моделирует периодическую орбиту с периодом 7:

Осуществленная на основании статистических данных [8] верификация периодической орбиты, смоделированной системой (1) с начальными условиями (2), позволяет получать прогнозируемые циклы для COVID-19, адаптированные к эпидемиологическим реалиям. Рисунок 1 содержит график смоделированного краткосрочного прогноза для возможных колебаний коронавирусной динамики на март 2022 г.

Коронавирусная эпидемия спровоцировала глобальный экономический кризис. В России [9, 10] по итогам 2020 г. ВВП на душу населения упал на 2.07%, нарушив тенденцию к росту в предыдущие до пандемии годы. Для математической интерпретации взаимного влияния пандемии и экономики мы воспользовались двумя уравнениями из предложенной В. Сандерсоном [5, 6] дискретной модели, которая называется моделью Wonderland (“Чудесная страна”) и описывает взаимосвязь экономических, демографических и экологических процессов.

В итоге получена математическая модель взаимного влияния пандемии и экономики:

Здесь коэффициенты $\gamma ,\eta ,\lambda ,\delta ,\rho ,\omega $ являются константами; y_j – ВВП на душу населения. Через z_j обозначается уровень преодоления пандемии ($0 \leqslant {{z}_{j}} \leqslant 1$). В случае ${{z}_{j}} = 1$ считается, что эпидемиологическая обстановка находится в идеальном состоянии и заражение COVID полностью отсутствует. Значение ${{z}_{j}} = 0$ выражает противоположный предельный случай, когда размеры пандемии настолько велики, что возникает максимальная угроза для человеческого здоровья и экономики.

Государство заинтересовано в преодолении пандемии, восстановлении экономического роста и возвращении социально-экономической обстановки в устойчивый режим. С математической точки зрения устойчивому режиму соответствует неподвижная точка системы (3). Для нахождения неподвижной точки правые части в (3) приравниваются соответственно S_j,I_j,R_j,V_j,z_j,y_j и вычисляются координаты неподвижной точки ${{w}_{\# }}$.

Поскольку для показателей заболеваемости и выздоровления характерна хаотичность, то в целях преодоления хаотичной динамики осуществим модификацию модели (3), используя результаты из современной теории управления хаосом. Введем обозначения

и запишем систему (3) в векторной форме: где

Совершив линеаризацию системы (4) в окрестности неподвижной точки w_# и затем применив метод Пирагаса [11], получим модифицированную систему:

где U(j) является функцией управления, предназначенной для стабилизации поведения решений системы. На основании результатов работ [12, 13] по стабилизации дискретных систем получается функция управления следующего вида:

Здесь P(j) – периодичная матрица, заданная формулой:

где $ - 1 < k < 1$, E – единичная матрица, О – нулевая матрица, $A\left( {{{w}_{\# }}} \right)$ – матрица Якоби для вектор-функции F, ${{w}_{\# }}$ – неподвижная точка.

Дискретная система (5) характеризуется сверхвысокой чувствительностью к изменениям параметров. Таким образом, за счет вариации коэффициентов модель (5) способна имитировать различные сценарии, которые вполне соответствуют реальным эпидемиологическим и экономическим процессам. При моделировании с помощью системы (5) будем использовать помесячную статистику.

В целях моделирования прогноза по преодолению пандемии и развитию экономики будем решать систему (5) с начальными условиями, которые соответствуют текущим реалиям. Согласно статистическим данным [8–10] на конец февраля 2022 г. имеем

В результате компьютерного эксперимента были подобраны численные значения параметров системы (5):

По многочисленным экспертным оценкам, в 2022 г. ВВП России может снизиться на 7% и более в результате западных санкций, направленных против российской военной спецоперации на Украине. В этой связи при моделировании для 2022 г. использовались коэффициенты

а для 2023 и 2024 г. применялись

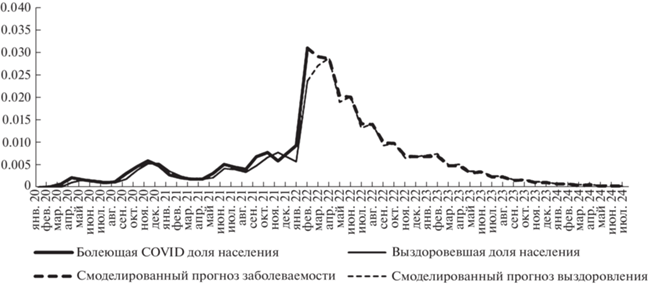
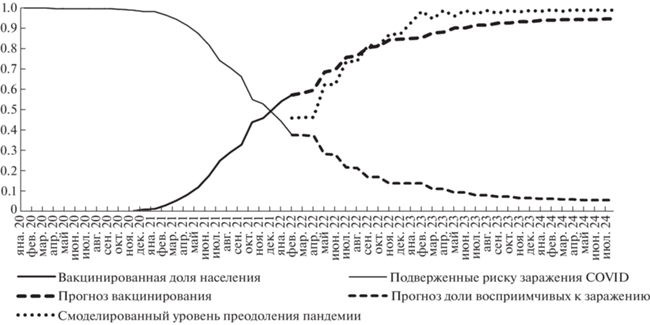
Решив систему (5) с начальными условиями (7) мы получили прогнозные траектории, графики которых представлены на рис. 2–4.

Графики рис. 2, 3 наглядно демонстрируют, что вакцинация населения является главным инструментом в борьбе с COVID-19. Кроме того, рис. 3, 4 указывают на существенную взаимосвязь между преодолением пандемии и восстановлением экономического роста. Коэффициент корреляции между полученными значениями w₅(j) и w₆(j) составляет 0.79.

Разработанная модель (5)–(6) является не только инструментом эффективного и адекватного прогнозирования. Основное достоинство этой модели заключается в том, что она дополнительно дает возможность практического управления динамикой пандемии и ВВП в целях стабилизации социально-экономического развития. Полученная в явном виде аналитическая формула (6) дает возможность определять конкретные размеры и время проведения упреждающих корректировок.

В результате вычислений и верификации, проведенных на основе итогов моделирования, и с учетом инвестиционного мультипликатора [14] были получены помесячные значения для масштабов вакцинирования и объемов дополнительных инвестиций, необходимых для преодоления пандемии и обеспечения экономического роста. Эти значения сведены в табл. 1, которая по сути является графиком проведения превентивных антикризисных мер.

На основании полученных результатов можно сделать вывод, что для преодоления пандемии и восстановления экономического роста необходимо своевременно осуществлять упреждающие корректирующие меры. Организацию и реализацию управленческих мер способны выполнить только государственные структуры. В соответствии с полученными в данной работе результатами моделирования, на среднесрочную перспективу первоочередными задачами государства являются полная реализация программы вакцинации и финансовая поддержка экономики в необходимых объемах и сроках.