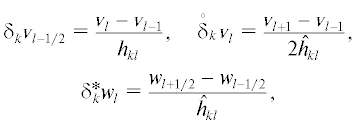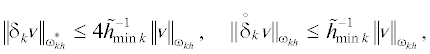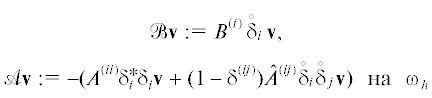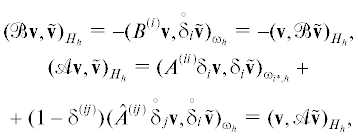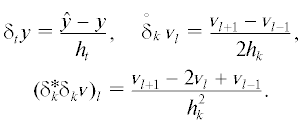Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 505, № 1, стр. 30-36

К настоящему времени разработан богатый набор численных методов решения системы уравнений газовой динамики [1–3]. В их число входят явные симметричные по пространству сеточные методы, основанные на предварительной квазигазодинамической (КГД) регуляризации этой системы [4–6]. Несмотря на многолетний успешный опыт практического применения таких методов, теория их устойчивости длительное время была развита слабо.

В данном сообщении изучается явная двухслойная симметричная по пространству разностная схема для линеаризованной на постоянном решении многомерной КГД системы уравнений. Для начально-краевой задачи на неравномерной прямоугольной сетке впервые даются достаточные условия L²-диссипативности типа Куранта с помощью энергетического метода; одномерный случай см. в [7]. Для задачи Коши на равномерной сетке усовершенствуются как необходимые, так и достаточные условия L²-диссипативности, недавно выведенные спектральным методом в [8]. Указывается новая форма задания параметра релаксации $\tau $, гарантирующая равномерную ограниченность сверху и снизу числа типа Куранта как от сетки, так и от числа Маха как в достаточных, так и в необходимом условии. В нее входят отношения модулей компонент скорости газа к шагам сетки по отдельным координатным направлениям.

1. Выпишем линеаризованную КГД систему уравнений. Пусть $\rho > 0$, ${\mathbf{u}} = ({{u}_{1}}, \ldots ,{{u}_{n}})$, $\varepsilon > 0$ – плотность, скорость, удельная внутренняя энергия газа зависят от (x, t), где $x = ({{x}_{1}}, \ldots ,{{x}_{n}}) \in \Omega $ и $t \geqslant 0$, а $\Omega $ – область в ${{\mathbb{R}}^{n}}$, $n = 1,2,3$. Введем $\mu = {{\alpha }_{s}}\tau p$, $\lambda = {{\alpha }_{{1s}}}\tau p$, $\tilde {\varkappa } = \gamma {{\hat {\alpha }}_{P}}\tau p$ – искусственные коэффициенты динамической и объемной вязкости и нормированный коэффициент теплопроводности, где $p = (\gamma - 1)\rho \varepsilon $ – давление, $\tau > 0$ – параметр релаксации, $\gamma > 1$ – показатель адиабаты, ${{\alpha }_{s}} \geqslant 0$ и $1{\text{/}}{{\hat {\alpha }}_{P}}$ – числа Шмидта и Прандтля с ${{\hat {\alpha }}_{P}} \geqslant 0$.

Рассмотрим постоянное решение $(\rho ,{\mathbf{u}},\varepsilon )(x,t)$ = = $({{\rho }_{*}},{{{\mathbf{u}}}_{*}},{{\varepsilon }_{*}})$, где ${{\rho }_{*}} > 0$, ${{{\mathbf{u}}}_{*}} = ({{u}_{{*1}}}, \ldots ,{{u}_{{*n}}})$, ${{\varepsilon }_{*}}$ > 0. Введем фоновые значения ${{\mu }_{*}}\, = \,{{\hat {\alpha }}_{s}}\tau {{\rho }_{*}}c_{*}^{2}$, ${{\lambda }_{*}}$ = = ${{\hat {\alpha }}_{{1s}}}\tau {{\rho }_{*}}c_{*}^{2}$, ${{\tilde {\varkappa }}_{*}} = {{\hat {\alpha }}_{P}}\tau {{\rho }_{*}}c_{*}^{2}$, где ${{c}_{*}} = \sqrt {\gamma (\gamma - 1){{\varepsilon }_{*}}} $ – фоновая скорость звука, ${{\hat {\alpha }}_{s}} = \frac{{{{\alpha }_{s}}}}{\gamma } \geqslant 0$, ${{\hat {\alpha }}_{{1s}}} = \frac{{{{\alpha }_{{1s}}}}}{\gamma }$; пусть ${{\hat {\alpha }}_{{1s}}} \geqslant - \frac{{{{{\hat {\alpha }}}_{s}}}}{3}$. Для фонового значения $\tau $ сохранено прежнее обозначение. Введем малые возмущения постоянного решения в виде $\left( {{{\rho }_{*}}\tilde {\rho },\frac{{{{c}_{*}}}}{{\sqrt \gamma }}{\mathbf{\tilde {u}}},\sqrt {\gamma - 1} {{\varepsilon }_{*}}\tilde {\varepsilon }} \right)$, где ${\mathbf{z}} = (\tilde {\rho },{\mathbf{\tilde {u}}},\tilde {\varepsilon }{{)}^{T}}$ – вектор-столбец безразмерных малых возмущений. Тогда линеаризованная КГД система дифференциальных уравнений 2-го порядка по x с постоянными коэффициентами такова:

в $\Omega $ при $t > 0$ аналогично [9]. Здесь операторы div и $\nabla = ({{\partial }_{1}}, \ldots ,{{\partial }_{n}})$ берутся по x, ${{\partial }_{t}} = \partial {\text{/}}\partial t$, ${{\partial }_{i}} = \partial {\text{/}}\partial {{x}_{i}}$ и ${\mathbf{M}}\nabla = {\mathbf{M}} \cdot \nabla $, ${\mathbf{M}}\nabla \rho = {\mathbf{M}} \cdot \nabla \rho $ и т.д., а $ \cdot $ означает скалярное произведение векторов. Также M = = ${{({{M}_{1}}, \ldots ,{{M}_{n}})}^{T}}$ и ${{M}_{k}} = \frac{{{{u}_{{*k}}}}}{{{{c}_{*}}}}$, ${{\gamma }_{*}} = \frac{\gamma }{{\gamma - 1}}$, ${{\hat {a}}_{0}}$ = = $\frac{1}{3}{{\hat {\alpha }}_{s}} + {{\hat {\alpha }}_{{1s}}} \geqslant 0$. Тогда $M = \left| {\mathbf{M}} \right| = \frac{{{\text{|}}{{{\mathbf{u}}}_{*}}{\text{|}}}}{{{{c}_{*}}}}$ – фоновое число Маха.

Указанную систему уравнений перепишем в симметричной матричной форме

где ${{B}^{{(i)}}}$ и ${{A}^{{(ii)}}}$, ${{\hat {A}}^{{(ij)}}}$ – матрицы конвективных и вязких слагаемых (порядка n + 2). Здесь и ниже по повторяющимся индексам i, j (и только по ним) предполагается суммирование от 1 до $n$, а ${{\delta }^{{(ij)}}}$ – символ Кронекера.

Запишем эти матрицы. Пусть ${{{\mathbf{e}}}_{0}}, \ldots ,{{{\mathbf{e}}}_{{n + 1}}}$ – векторы-столбцы стандартного координатного базиса в ${{\mathbb{R}}^{{n + 2}}}$. Введем симметричные матрицы E^{(k, l)} := := ${{{\mathbf{e}}}_{k}}{\mathbf{e}}_{l}^{T} + {{{\mathbf{e}}}_{l}}{\mathbf{e}}_{k}^{T}$, тогда

при всех $k,l$ от 1 до n (так же, как и в [8]). Здесь и ниже I_l – единичная матрица порядка l, diag{d₁₁, ..., ${{d}_{{(n + 2)(n + 2)}}}\} $ – диагональная матрица с перечисленными диагональными элементами. Матрицы ${{B}^{{(k)}}}$, ${{A}^{{(kk)}}}$, ${{\hat {A}}^{{(kl)}}}$ – симметричные и ${{\hat {A}}^{{(kl)}}} = {{\hat {A}}^{{(lk)}}}$.

Матрицы ${{A}^{{(kk)}}}$ и ${{B}^{{(k)}}}$ связаны формулой [8]

где $D: = {\text{diag}}\{ 0,{{\hat {\alpha }}_{s}}, \ldots ,{{\hat {\alpha }}_{s}},{{\hat {\alpha }}_{P}}\} $ – матрица порядка n + 2.

Матрицы ${{B}^{{(k)}}}$, ${{A}^{{(kk)}}}$, ${{\hat {A}}^{{(kl)}}}$ ($k \ne l$) можно также записать в 3 × 3-блочном виде, см. [9] (где в диагональных элементах ${{A}^{{(kk)}}}$ следует убрать $\sqrt \cdot $ в $\sqrt \gamma $, $\sqrt {{{\gamma }_{*}}} $).

Для решения задачи Коши для системы уравнений типа (1) известна оценка

где ${\mathbf{z}}{{{\text{|}}}_{{t = 0}}} = {{{\mathbf{z}}}_{0}}$; аналогичная оценка верна и для начально-краевой задачи с однородным краевым условием Дирихле. Они явились исходными для анализа свойства диссипативности аппроксимирующей явной симметричной разностной схемы.

2. Рассмотрим сначала условия диссипативности абстрактной двухслойной явной разностной схемы. Пусть ${{H}_{h}}$ – семейство евклидовых пространств со скалярным произведением ${{( \cdot , \cdot )}_{{{{H}_{h}}}}}$ и нормой ${{\left\| {\, \cdot \,} \right\|}_{{{{H}_{h}}}}}$. Пусть $\left\| {\, \cdot \,} \right\|$ – согласованная с ${{\left\| {\, \cdot \,} \right\|}_{{{{H}_{h}}}}}$ норма в пространстве линейных операторов $\mathcal{L}[{{H}_{h}}]$, действующих в H_h. Пусть I – единичный оператор.

Введем неравномерную сетку ${{\bar {\omega }}^{{{{h}_{t}}}}}$ с узлами $0 = {{t}_{0}} < {{t}_{1}} < \ldots < {{t}_{{\bar {m}}}} = T$ на $[0,T]$ и шагами ${{h}_{{tm}}} = {{t}_{m}} - {{t}_{{m - 1}}}$. Пусть ${{\omega }^{{{{h}_{t}}}}} = {{\bar {\omega }}^{{{{h}_{t}}}}}{{\backslash }}T$ и ${{y}^{m}} = y({{t}_{m}})$. Определим сеточные операторы

Рассмотрим явную двухслойную разностную схему

с ${{G}_{m}} \in \mathcal{L}[{{H}_{h}}]$. Функция $y$: ${{\bar {\omega }}^{{{{h}_{t}}}}} \to {{H}_{h}}$ – искомая, а ${{y}^{0}} \in {{H}_{h}}$ и $b$: ${{\omega }^{{{{h}_{t}}}}} \to {{H}_{h}}$ заданы.

Теорема 1. Пусть $\mathop {\max }\nolimits_{0 \leqslant m \leqslant \bar {m} - 1} \left\| {I\, - \,{{h}_{{t(m + 1)}}}{{G}_{m}}} \right\|\, \leqslant \,1$ или, эквивалентно,

в частности, ${{G}_{m}} \geqslant 0$. Тогда для схемы (3) верна оценкаа при b = 0 схема H_h-диссипативна: ${\text{||}}{{y}^{{\bar {m}}}}{\text{|}}{{{\text{|}}}_{{{{H}_{h}}}}} \leqslant {\text{||}}{{y}^{{\bar {m} - 1}}}{\text{|}}{{{\text{|}}}_{{{{H}_{h}}}}} \leqslant \ldots \leqslant {\text{||}}{{y}^{0}}{\text{|}}{{{\text{|}}}_{{{{H}_{h}}}}}$ при всех ${{y}^{0}} \in {{H}_{h}}$.

Если операторы $I - {{h}_{{t(m + 1)}}}{{G}_{m}}$, $0 \leqslant m \leqslant \bar {m} - 2$ обратимы, то условие (4) не только достаточно, но и необходимо для справедливости свойства ${{H}_{h}}$-диссипативности.

Если операторы ${{G}_{m}}$, $0 \leqslant m \leqslant \bar {m} - 1$ обратимы, то условие (4) можно переписать в виде

Ниже интерес представляет следующая запись явной двухслойной схемы (3)

где $\mathcal{B},\mathcal{A} \in \mathcal{L}({{H}_{h}})$ – операторы конвективных и вязких (без учета τ) слагаемых такие, что $\mathcal{B}{\kern 1pt} * = - \mathcal{B}$, $\mathcal{A}{\kern 1pt} * = \mathcal{A}$. Они и $\tau > 0$ могут зависеть от t_m. Также ${{c}_{*}} > 0$ – нормировочный множитель. Фактически здесь $c_{*}^{2}\tau \mathcal{A} = \frac{1}{2}(G + G{\kern 1pt} *)$, ${{c}_{*}}\mathcal{B}$ = $\frac{1}{2}(G$ – – G*).

Пусть ${{\lambda }_{{\max }}}(\mathcal{A})$ – максимальное собственное значение оператора $\mathcal{A}$.

Теорема 2. Пусть операторы $\mathcal{B}$ и $\mathcal{A}$ связаны неравенством

и ${{\lambda }_{{\max }}}(\mathcal{A}) \leqslant \tilde {\lambda }$. Если также ${{h}_{t}}$ подчиняется условиюто оператор $G = {{c}_{*}}\mathcal{B} + c_{*}^{2}\tau \mathcal{A}$ удовлетворяет неравенству (4), и поэтому для решения явной схемы (6) верна оценка (5), а при b = 0 – свойство H_h-диссипативности.

Операторный вид неравенства (7) таков: $ - {{\mathcal{B}}^{2}} \leqslant {{c}_{A}}\mathcal{A}$, где $( - {{\mathcal{B}}^{2}}){\kern 1pt} * = - {{\mathcal{B}}^{2}} \geqslant 0$.

В довольно типичном варианте шаг по времени ${{h}_{t}}$ и параметр $\tau $ задаются формулами ${{h}_{t}} = \frac{{\beta \hat {h}}}{{{{c}_{*}}}}$, ${{\tau }_{*}} = \frac{{\alpha \hat {h}}}{{{{c}_{*}}}}$ [4–6], где $\hat {h}$ – некоторый характерный шаг сетки по пространству, а $\beta > 0$ (число типа Куранта) и $\alpha > 0$ – параметры. Выбор $\hat {h}$ отнюдь не очевиден заранее и должен определяться в результате анализа устойчивости схемы. Тогда условие (8) принимает вид

т.е. форму условия на $\beta $ в зависимости от $\alpha $. Обратим внимание на то, что

Указанное значение ${{\alpha }_{{{\text{opt}}}}}$ важно знать на практике как позволяющее максимально расширить условие на ${{h}_{t}}$. Отметим, что $\beta _{{{\text{suf}}}}^{{(0)}}(\alpha )$ возрастает на $(0,{{\alpha }_{{{\text{opt}}}}}]$, убывает на $[{{\alpha }_{{{\text{opt}}}}}, + \infty )$ и $\beta _{{suf}}^{{(0)}}(\alpha ) \to 0$ при $\alpha \to + 0$ и $\alpha \to + \infty $.

3. Выпишем разностную схему для линеаризованной КГД системы уравнений (1) и выполним энергетический анализ ее устойчивости. Пусть $\Omega = (0,{{X}_{1}}) \times \ldots \times (0,{{X}_{n}})$. При $k = 1, \ldots ,n$ введем на $[0,{{X}_{k}}]$ произвольную неравномерную сетку ${{\bar {\omega }}_{{kh}}}$ по переменной x_k с узлами 0 = ${{x}_{{k0}}} < {{x}_{{k1}}} < \ldots < {{x}_{{k{{N}_{k}}}}}$ = = X_k и шагами ${{h}_{{kl}}} = {{x}_{{kl}}} - {{x}_{{k(l - 1)}}}$. Пусть ω_kh = = ${{\bar {\omega }}_{{kh}}}{{\backslash }}\{ 0,{{X}_{k}}\} $. Введем также сетку $\omega _{{kh}}^{*}$ с узлами ${{x}_{{k(l - 1/2)}}} = \frac{1}{2}({{x}_{{k(l - 1)}}} + {{x}_{{kl}}})$, $1 \leqslant l \leqslant {{N}_{k}}$ и шагами ${{\hat {h}}_{{kl}}} = ({{h}_{{kl}}} + {{h}_{{k(l + 1)}}}){\text{/}}2$.

Введем разностные отношения

где ${{v}_{l}} = v({{x}_{{kl}}})$, ${{w}_{{l - 1/2}}} = w({{x}_{{k(l - 1/2)}}})$, скалярные произведения и отвечающие им нормы ${{\left\| {\, \cdot \,} \right\|}_{{{{\omega }_{{kh}}}}}}$, ${{\left\| {\, \cdot \,} \right\|}_{{\omega _{{kh}}^{*}}}}$.

Лемма 1. Пусть функция ${v}$ определена на ${{\bar {\omega }}_{{kh}}}$. Верно неравенство 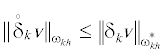[9]. Если $v{{{\text{|}}}_{{l = 0,{{N}_{k}}}}}$ = = 0, то верны также неравенства

где ${{\tilde {h}}_{{\min k}}}$ := ${{\min }_{{1 \leqslant l \leqslant {{N}_{k}} - 1}}}\sqrt {{{h}_{{kl}}}{{h}_{{k(l + 1)}}}} \geqslant {{h}_{{\min k}}}$ := := ${{\min }_{{1 \leqslant l \leqslant {{N}_{k}}}}}{{h}_{{kl}}}$.

Введем n-мерные сетки ${{\bar {\omega }}_{h}} = {{\bar {\omega }}_{{1h}}} \times \ldots \times {{\bar {\omega }}_{{nh}}}$, ${{\omega }_{h}} = {{\omega }_{{1h}}} \times \ldots \times {{\omega }_{{nh}}}$, $\partial {{\omega }_{h}} = {{\bar {\omega }}_{h}}{{\backslash }}{{\omega }_{h}}$ и ${{\omega }_{{i*,h}}}$, отличающуюся от ${{\omega }_{h}}$ заменой ${{\omega }_{{ih}}}$ на $\omega _{{ih}}^{*}$, $1 \leqslant i \leqslant n$. Введем скалярные произведения функций ${{(v,\tilde {v})}_{{{{\omega }_{h}}}}}$ = = ${{( \ldots {{(v\tilde {v},1)}_{{{{\omega }_{{1h}}}}}}, \ldots ,1)}_{{{{\omega }_{{nh}}}}}}$ и n + 2-мерных вектор-функций ${{({\mathbf{v}},{\mathbf{\tilde {v}}})}_{{{{\omega }_{h}}}}} = ( \ldots {{({\mathbf{v}} \cdot {\mathbf{\tilde {v}}},1)}_{{{{\omega }_{{1h}}}}}}, \ldots {{,1)}_{{{{\omega }_{{nh}}}}}}$, а также отвечающие им нормы ${{\left\| v \right\|}_{{{{\omega }_{h}}}}}$ и ${{\left\| {\mathbf{v}} \right\|}_{{{{\omega }_{h}}}}}$. Пусть скалярные произведения ${{( \cdot , \cdot )}_{{{{\omega }_{{i{\kern 1pt} *,h}}}}}}$ отличаются от ${{( \cdot , \cdot )}_{{{{\omega }_{h}}}}}$ заменой ${{( \cdot ,1)}_{{{{\omega }_{{ih}}}}}}$ на ${{( \cdot ,1)}_{{\omega _{{ih}}^{*}}}}$, $1 \leqslant i \leqslant n$. Введем ${{H}_{h}}$ – пространство вектор-функций-столбцов v: ${{\bar {\omega }}_{h}} \to {{\mathbb{R}}^{{n + 2}}}$ с ${\mathbf{v}}{{{\text{|}}}_{{\partial {{\omega }_{h}}}}} = 0$, со скалярным произведением ${{(v,\tilde {v})}_{{{{H}_{h}}}}} = (v,\tilde {v}{{)}_{{{{\omega }_{h}}}}}$.

Введем операторы $\mathcal{B},\;\mathcal{A}$: ${{H}_{h}} \to {{H}_{h}}$ такие, что

для ${\mathbf{v}} \in {{H}_{h}}$ [9]. В силу симметрии матриц ${{B}^{{(k)}}}$, ${{A}^{{(kk)}}}$, ${{\hat {A}}^{{(kl)}}}$ для любых ${\mathbf{v}},{\mathbf{\tilde {v}}} \in {{H}_{h}}$ имеем т.е. верны свойства $\mathcal{B}{\kern 1pt} * = - \mathcal{B}$ и поэтому ${{(\mathcal{B}{\mathbf{v}},{\mathbf{v}})}_{{{{H}_{h}}}}} = 0$ для ${\mathbf{v}} \in {{H}_{h}}$, а также $\mathcal{A}{\kern 1pt} * = \mathcal{A}$.

КГД систему уравнений (1) в $\Omega \times (0,T)$ при краевом условии ${\mathbf{z}}{{{\text{|}}}_{{\partial \Omega \times (0,T)}}} = 0$ аппроксимируем явной по t разностной схемой, трехточечной по каждому направлению ${{x}_{1}}, \ldots ,{{x}_{n}}$:

с искомой функцией y: ${{\bar {\omega }}^{{{{h}_{t}}}}} \to {{H}_{h}}$. Функции ${{y}^{0}} \in {{H}_{h}}$ и b: ${{\omega }^{{{{h}_{t}}}}} \to {{H}_{h}}$ заданы, причем b добавлена для полноты анализа устойчивости.

Введем вспомогательные матрицы [9]

Лемма 2. Пусть ${{\mathop {{\text{div}}}\limits^ \circ }_{h}}{\kern 1pt} {\mathbf{u}}: = {{\mathop \delta \limits^ \circ }_{i}}{\kern 1pt} {{{v}}_{i}}$ и ${\mathbf{u}} = ({{v}_{1}}, \ldots ,{{v}_{n}})$. Справедливы формула и неравенства

Формула (16) следует из (13) и близкой формулы, выведенной в [9, доказательство теоремы 1]. Неравенства следуют из нее c помощью (2), (15) и первого неравенства леммы 1.

Лемма 3. Пусть ${{\tilde {h}}_{{\min }}} = {{\min }_{{1 \leqslant k \leqslant n}}}{{\tilde {h}}_{{\min k}}}$. Справедлива оценка

Указанная оценка выводится на основе формулы Рэлея для ${{\lambda }_{{\max }}}(\mathcal{A})$ и аккуратной оценки правой части формулы (16), в том числе с учетом неравенств (11) и формулы для спектральной нормы $\left\| {{{B}^{{(k)}}}} \right\| = \left| {{{M}_{k}}} \right| + 1$, $1 \leqslant k \leqslant n$.

Устойчивость схемы (14) непосредственно следует из теоремы 2 с учетом (9) в силу свойств $\mathcal{B}{\kern 1pt} * = - \mathcal{B}$, $\mathcal{A}{\kern 1pt} * = \mathcal{A}$, неравенства (17) (согласно которому c_A = 1) и леммы 3.

Теорема 3. При условии

для b = 0 схема (14) является H_h-диссипативной, а в общем случае для нее верна оценка

Формулы (10) принимают вид

На основании леммы 3 естественно ввести характерный шаг $\hat {h} > 0$ такой, что

Для простоты (также обстоит дело на практике) он не зависит от параметров ${{\hat {\alpha }}_{s}}$, ${{\hat {\alpha }}_{{1s}}}$, ${{\hat {\alpha }}_{P}}$. Тогда верны двусторонние оценки $n + 3 \leqslant {{\hat {h}}^{2}}\tilde {\lambda } \leqslant n + 3$ + + $\max \{ 4{{\hat {\alpha }}_{s}} + (n + 3){{\hat {a}}_{0}},4{{\hat {\alpha }}_{P}}\} $, равномерные относительно ${{\bar {\omega }}_{h}}$ и M. Поэтому и $\beta _{{{\text{suf}}}}^{{(0)}}(\alpha )$, $\beta _{{{\text{suf}}}}^{{(0)}}({{\alpha }_{{{\text{opt}}}}})$, ${{\alpha }_{{{\text{opt}}}}}$ равномерно ограничены снизу и сверху равномерно относительно ${{\bar {\omega }}_{h}}$ и M. Первое существенно для расчетов на сильно неравномерных сетках, а второе – для моделирования любых течений от дозвуковых до сверх- и гиперзвуковых. Возникают такие формулы для параметров $\beta $ и $\tau $

4. Перейдем к спектральному анализу разностной схемы на равномерной сетке. Пусть теперь ${{\omega }_{{kh}}}$ и ${{\bar {\omega }}^{{{{h}_{t}}}}}$ – равномерные сетки по x_k и t с узлами $l{{h}_{k}}$, $l \in \mathbb{Z}$ и ${{t}_{m}} = m{{h}_{t}}$, $m \geqslant 0$, и шагами ${{h}_{k}} > 0$ и ${{h}_{t}} > 0$, $1 \leqslant k \leqslant n$. Разностные операторы принимают упрощенный вид

Пусть ${{\omega }_{h}}: = {{\omega }_{{1h}}} \times \ldots \times {{\omega }_{{nh}}}$ и $h = ({{h}_{1}}, \ldots ,{{h}_{n}})$.

С использованием операторов (12) аппроксимируем линеаризованную КГД систему уравнений (1) в ${{\mathbb{R}}^{n}} \times (0,\infty )$ явной двухслойной разностной схемой

Пусть H_h – гильбертово пространство вектор-функций ${\mathbf{v}}$: ${{\omega }_{h}} \to {{\mathbb{C}}^{{n + 2}}}$, суммируемых в квадрате на ${{\omega }_{h}}$, со скалярным произведением ${{({\mathbf{v}},{\mathbf{y}})}_{{{{H}_{h}}}}}$ = = ${{h}_{1}} \ldots {{h}_{n}}\sum\limits_{{\mathbf{k}} \in {{\mathbb{Z}}^{n}}}^{} {{{{({{{\mathbf{v}}}_{{\mathbf{k}}}},{{{\mathbf{y}}}_{{\mathbf{k}}}})}}_{{{{\mathbb{C}}^{{n + 2}}}}}}} $, ${\mathbf{k}} = ({{k}_{1}}, \ldots ,{{k}_{n}})$. Будем изучать условия справедливости оценки

при любых ${{{\mathbf{y}}}^{0}} \in {{{\mathbf{H}}}_{h}}$ и b: ${{\bar {\omega }}^{{{{h}_{t}}}}} \to {{{\mathbf{H}}}_{h}}$. При b = 0 эта оценка принимает вид и она эквивалентна как оценке ${{\left\| \mathcal{T} \right\|}_{{\mathcal{L}[{{{\mathbf{H}}}_{h}}]}}} \leqslant 1$ нормы ограниченного оператора перехода со слоя на слой $\mathcal{T} = I - {{h}_{t}}({{c}_{*}}\mathcal{B} + \tau c_{*}^{2}\mathcal{A})$, так и свойству H_h-диссипативности

При условии ${{\left\| \mathcal{T} \right\|}_{{\mathcal{L}[{{{\mathbf{H}}}_{h}}]}}} \leqslant 1$ оценка (23) верна, и ниже можно ограничиться случаем b = 0.

Пусть ${{h}_{t}}$ и $\tau $ задаются указанными выше формулами. В соответствии со спектральным методом, см. [10, 11] и [8], рассмотрим частные решения схемы (22) при b = 0 вида

где i – мнимая единица, а ξ – параметр. Их подстановка в (22) приводит к рекуррентной формуле ${\mathbf{\hat {w}}} = {{G}_{{\mathbf{s}}}}{\mathbf{w}}$ на ${{\bar {\omega }}^{{{{h}_{t}}}}}$, где G_s – символ оператора $\mathcal{T}$ с ${\mathbf{s}} = ({{s}_{1}}, \ldots ,{{s}_{n}})$ такой, что

Здесь sgn0 = 1. Ниже ${\mathbf{s}} \in S: = [ - {{1,1]}^{n}}$ берется в качестве параметра вместо ξ; ясно, что ${{\sigma }_{k}} = 1 - s_{k}^{2}$.

Введем вектор-строку ${\mathbf{\zeta }} = ({{\zeta }_{1}}, \ldots ,{{\zeta }_{n}})$ с ${{\zeta }_{k}} = {{d}_{k}}{{s}_{k}}$, $1 \leqslant k \leqslant n$. Пусть $d = (d_{1}^{2} + \ldots + d_{n}^{2}{{)}^{{1/2}}}$.

Следующие два важных результата взяты из [8, лемма 1 и теорема 2].

Лемма 4. 1. Матрицы B_s и A_s можно записать в 3 × 3-блочной форме

с использованием обозначений и $Q: = {\text{diag}}\{ {{q}_{1}}, \ldots ,{{q}_{n}}\} $ с ${{q}_{k}}: = d_{k}^{2}{{\sigma }_{k}} = r_{k}^{2}\sigma _{k}^{2}$, $1 \leqslant k \leqslant n$, а также ${{\hat {a}}_{1}} = {{\hat {a}}_{0}} + 1$.

2. Верно матричное неравенство: $B_{{\mathbf{s}}}^{2} \leqslant {{A}_{{\mathbf{s}}}}$ при всех $s \in S: = [ - {{1,1]}^{n}}$.

Теорема 4. Выполнение матричного неравенства

необходимо и достаточно, а выполнение числового неравенствас ${{\max }_{{{\mathbf{s}} \in S}}}{{\lambda }_{{\max }}}({{A}_{{\mathbf{s}}}}) \leqslant \bar {\lambda }$ достаточно для справедливости свойства (25).

Новое необходимое условие выводится из критерия (26) анализом случаев s = 0 и ${\mathbf{\xi }} = 2\varepsilon {\mathbf{\tilde {\xi }}}$ с $\varepsilon \to + 0$, ${\mathbf{\tilde {\xi }}} = ({{\tilde {\xi }}_{1}}, \ldots ,{{\tilde {\xi }}_{n}}) \ne 0$ на основе леммы 4 (как и недавно в баротропном случае [12]).

Теорема 5. Пусть ${{r}_{{\max }}}: = {{\max }_{{1 \leqslant k \leqslant n}}}{{r}_{k}}$ и ${{r}^{2}} = r_{1}^{2} + ... + r_{n}^{2}$. Выполнение неравенства

где $\hat {\lambda }$ := $\frac{1}{2}\left[ {1 + {{{\hat {\alpha }}}_{P}} + \sqrt {{{{({{{\hat {\alpha }}}_{P}} - 1)}}^{2}} + \frac{4}{{{{\gamma }_{*}}}}{{{\hat {\alpha }}}_{P}}} } \right]$ ≥ ≥ $\max \left\{ {{{{\hat {\alpha }}}_{P}} + \frac{1}{{{{\gamma }_{*}}}},1} \right\}$, необходимо для справедливости свойства (25). Здесь $\frac{1}{n} \leqslant \frac{{r_{{\max }}^{2}}}{{{{r}^{2}}}} \leqslant 1$.

Легко видеть, что верны формулы и двустороннее неравенство

Также ${{\beta }_{{{\text{suf}}}}}(\alpha ) \to 0$ и ${{\beta }_{{{\text{nec}}}}}(\alpha ) \to 0$ при $\alpha \to + 0$ или $\alpha \to + \infty $.

Для применения достаточного условия (27) укажем новую оценку сверху для ${{\lambda }_{{\max }}}({{A}_{{\mathbf{s}}}})$. Она выводится на основе формулы Рэлея для ${{\lambda }_{{\max }}}({{A}_{{\mathbf{s}}}})$ и аккуратной оценки квадратичной формы, отвечающей матрице A_s из леммы 4.

Теорема 6. При $n = 2,3$ верна оценка сверху

с ${{c}_{2}} = 1$, ${{c}_{3}} = \frac{9}{8}$, любым $\varepsilon > 0$ и $\hat {\lambda }$, указанным в теореме 5.

Согласно указанным оценкам, естественен выбор $\hat {h}$ (зависящий только от h и M) [12]

Для него верны равенства $r_{i}^{2}(M_{i}^{2} + 1) = \frac{{{{{\hat {h}}}^{2}}}}{{h_{i}^{2}}}(M_{i}^{2}$ + + 1) = 1, благодаря которым правую часть оценки (29) можно оценить (взяв минимум по ε > 0) как

где $C: = \max \{ \hat {\lambda },{{\hat {\alpha }}_{s}} + {{\hat {a}}_{1}}{{c}_{n}}\} \geqslant {{c}_{n}}$. Также $\underline \lambda \geqslant 1$ в необходимом условии (28), что приводит к необходимому условию и достаточному условию, не зависящим от h и M.

Отметим, что при этом возникают формулы для числа Куранта и параметра $\tau $

Они несущественно отличаются от выписанных выше в случае неравномерной сетки. Для других схем подобная формула для $\beta $ без степеней 2 (но с ${\text{|}}{{u}_{{*1}}}{\text{|}}, \ldots ,{\text{|}}{{u}_{{*n}}}{\text{|}}$) и $1{\text{/}}2$ имеется в [1, раздел 2.6].