Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 506, № 1, стр. 73-82

1. ВВЕДЕНИЕ

Обыкновенная цепная дробь действительного числа имеет весьма изящную геометрическую интерпретацию, позволяющую перейти от классического случая к многомерному (см. [1] и, например, [2–4]). Для описания такого обобщения рассмотрим ${{l}_{1}}, \ldots ,{{l}_{n}}$ – одномерные подпространства пространства ${{\mathbb{R}}^{n}}$, линейная оболочка которых совпадает со всем ${{\mathbb{R}}^{n}}$. Гиперпространства, натянутые на всевозможные (n – 1)-наборы из этих подпространств, разбивают ${{\mathbb{R}}^{n}}$ на 2ⁿ симплициальных конусов. Будем обозначать множество этих конусов через

Симплициальный конус с вершиной в начале координат 0 будем называть иррациональным, если линейная оболочка любой его гиперграни не содержит целых точек, кроме начала координат 0.

Определение 1. Пусть C – иррациональный конус, $C \in \mathcal{C}({{l}_{1}}, \ldots ,{{l}_{n}})$. Выпуклая оболочка $\mathcal{K}(C)\, = \,{\text{conv}}(C \cap {{\mathbb{Z}}^{n}}{{\backslash }}\{ {\mathbf{0}}\} )$ и его граница $\partial (\mathcal{K}(C))$ называются соответственно полиэдром Клейна и парусом Клейна, соответствующими конусу C. Объединение же всех 2ⁿпарусов

называется (n – 1)-мерной цепной дробью.

Особенный интерес представляет так называемый алгебраический случай. Напомним, что оператор из ${\text{G}}{{{\text{L}}}_{n}}(\mathbb{Z})$ с вещественными собственными значениями, характеристический многочлен которого неприводим над $\mathbb{Q}$, называется гиперболическим. Справедливо следующее утверждение о связи гиперболических операторов с алгебраическими числами в случае произвольного n (подробности см., например, в [5]).

Предложение 1. Числа $1,{{\alpha }_{1}}, \ldots ,{{\alpha }_{{n - 1}}}$ образуют базис некоторого вполне вещественного расширения K поля $\mathbb{Q}$ тогда и только тогда, когда вектор $(1,{{\alpha }_{1}}, \ldots ,{{\alpha }_{{n - 1}}})$ является собственным для некоторого гиперболического оператора $A \in {\text{S}}{{{\text{L}}}_{n}}(\mathbb{Z})$. При этом вектора $(1,{{\sigma }_{i}}({{\alpha }_{1}}), \ldots ,{{\sigma }_{i}}({{\alpha }_{{n - 1}}}))$, $i = 1, \ldots ,n$, где ${{\sigma }_{1}}( = {\text{id}}),{{\sigma }_{2}}, \ldots ,{{\sigma }_{n}}$ – все вложения K в $\mathbb{R}$, образуют собственный базис оператора A.

В случае n = 2 предложение 1 позволяет геометрически проинтерпретировать классическую теорему Лагранжа о периодичности обыкновенной цепной дроби. Геометрически теорема Лагранжа означает, что последовательность целочисленных длин и углов паруса одномерной цепной дроби ${\text{CF}}({{l}_{1}},{{l}_{2}})$ периодична тогда и только тогда, когда направления l₁ и l₂ являются собственными для некоторого ${\text{S}}{{{\text{L}}}_{2}}(\mathbb{Z})$ оператора с различными вещественными собственными значениями (см., например [6]).

Определение 2. Пусть ${{l}_{1}}, \ldots ,{{l}_{n}}$ – собственные подпространства некоторого гиперболического оператора $A \in {\text{G}}{{{\text{L}}}_{n}}(\mathbb{Z})$. Тогда $(n - 1)$-мерная цепная дробь ${\text{CF}}({{l}_{1}}, \ldots ,{{l}_{n}})$ называется алгебраической. Мы будем также говорить, что эта дробь ассоциирована с оператором A и писать CF(A) = ${\text{CF}}({{l}_{1}}, \ldots ,{{l}_{n}})$. Множество всех $(n - 1)$-мерных алгебраических цепных дробей будем обозначать ${{\mathfrak{A}}_{{n - 1}}}$.

Будем называть группой симметрий алгебраической цепной дроби ${\text{CF}}(A) = {\text{CF}}({{l}_{1}}, \ldots ,{{l}_{n}})$ множество

Из соображений непрерывности ясно, что для каждого $G \in {\text{Sy}}{{{\text{m}}}_{\mathbb{Z}}}({\text{CF}}(A))$ однозначно определена перестановка ${{\sigma }_{G}}$, такая что

И обратно, если для $G \in {\text{G}}{{{\text{L}}}_{n}}(\mathbb{Z})$ существует такая перестановка ${{\sigma }_{G}}$, что выполняются соотношения (1.1), то $G \in {\text{Sy}}{{{\text{m}}}_{\mathbb{Z}}}({\text{CF}}(A))$.

Благодаря теореме Дирихле об алгебраических единицах существует изоморфная ${{\mathbb{Z}}^{{n - 1}}}$ подгруппа группы ${\text{Sy}}{{{\text{m}}}_{\mathbb{Z}}}({\text{CF}}(A))$ (см., например, [5]). Относительно действия этой подгруппы на любом из 2ⁿ парусов возникает фундаментальная область, которую можно отождествить с $(n - 1)$-мерным тором (см. [2]). Для каждого элемента G, принадлежащего этой подгруппе, ${{\sigma }_{G}} = {\text{id}}$. Однако в ${\text{Sy}}{{{\text{m}}}_{\mathbb{Z}}}({\text{CF}}(A))$, вообще говоря, могут существовать такие элементы G, для которых ${{\sigma }_{G}} \ne {\text{id}}$.

Определение 3. Оператор $G\, \in \,{\text{Sy}}{{{\text{m}}}_{\mathbb{Z}}}({\text{CF}}(A))$ такой, что ${{\sigma }_{G}} = {\text{id}}$, будем называть симметрией Дирихле дроби ${\text{CF}}(A) \in {{\mathfrak{A}}_{{n - 1}}}$.

Определение 4. Оператор $G\, \in \,{\text{Sy}}{{{\text{m}}}_{\mathbb{Z}}}({\text{CF}}(A))$, не являющийся симметрией Дирихле, будем называть палиндромической симметрией дроби ${\text{CF}}(A)$. Если множество палиндромических симметрией цепной дроби непусто, то такую цепную дробь будем называть палиндромичной.

Определение 5. Палиндромическая симметрия $G \in {\text{Sy}}{{{\text{m}}}_{\mathbb{Z}}}({\text{CF}}(A))$ называется собственной, если у оператора G существует неподвижная точка на некотором парусе цепной дроби ${\text{CF}}(A)$. Палиндромическая симметрия $G \in {\text{Sy}}{{{\text{m}}}_{\mathbb{Z}}}({\text{CF}}(A))$, не являющаяся собственной, называется несобственной.

В данной работе нас будут интересовать собственные палиндромические симметрии ${\text{CF}}(A)$ в размерности n = 4. А именно, мы докажем критерий наличия такого рода симметрий у цепной дроби ${\text{CF}}(A)$. Для размерностей n = 2 и n = 3 аналогичные критерии уже существуют.

Для n = 2, т.е. для одномерных цепных дробей, палиндромичность напрямую связана с симметричностью периодов обыкновенных цепных дробей квадратичных иррациональностей. Критерий симметричности периода цепной дроби квадратичной иррациональности восходит к результатам Галуа [7], Лежандра [8], Перрона [9] и Крайтчика [10]. В работе [6] дано геометрическое доказательство этого критерия. Аналог этого критерия для n = 3 был получен в работе [5]. Упомянутые критерии выглядят следующим образом:

Предложение 2. Пусть ${\text{CF}}({{l}_{1}},{{l}_{2}}) \in {{\mathfrak{A}}_{1}}$ и пусть подпространство ${{l}_{1}}$ порождено вектором $(1,\alpha )$. Тогда ${\text{CF}}({{l}_{1}},{{l}_{2}})$ имеет собственную симметрию в том и только в том случае, если существует такое алгебраическое число $\omega $ степени 2 со своим сопряженным $\omega '$, что выполнено хотя бы одно из следующих условий:

(а) $(1,\alpha ) \sim (1,\omega )$: ${\text{Tr}}(\omega ) = \omega + \omega {\kern 1pt} ' = 0$;

(б) $(1,\alpha ) \sim (1,\omega )$: ${\text{Tr}}(\omega ) = \omega + \omega {\kern 1pt} ' = 1$.

Предложение 3. Пусть ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}}) \in {{\mathfrak{A}}_{2}}$ и пусть подпространство ${{l}_{1}}$ порождено вектором $(1,\alpha ,\beta )$. Тогда ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}})$ имеет собственную симметрию в том и только в том случае, если существует такое алгебраическое число $\omega $ степени $3$ со своими сопряженными $\omega {\kern 1pt} '$ и $\omega {\kern 1pt} '{\kern 1pt} '$, что выполнено хотя бы одно из следующих условий:

(а) $(1,\alpha ,\beta ) \sim (1,\omega ,\omega {\kern 1pt} ')$: ${\text{Tr}}(\omega ) = \omega + \omega {\kern 1pt} '\; + \omega {\kern 1pt} '{\kern 1pt} ' = 0$;

(б) $(1,\alpha ,\beta ) \sim (1,\omega ,\omega {\kern 1pt} ')$: ${\text{Tr}}(\omega ) = \omega + \omega {\kern 1pt} '\; + \omega {\kern 1pt} '{\kern 1pt} ' = 1$.

При выполнении утверждения (а) или (б) кубическое расширение $\mathbb{Q}(\alpha ,\beta )$ будет нормальным.

В этих формулировках ${{{\mathbf{v}}}_{1}} \sim {{{\mathbf{v}}}_{2}}$ для векторов из ${{\mathbb{R}}^{n}}$ означает существование такого оператора $X\, \in \,{\text{G}}{{{\text{L}}}_{n}}(\mathbb{Z})$ и такого ненулевого $\mu \in \mathbb{R}$, что $X{{{\mathbf{v}}}_{1}} = \mu {{{\mathbf{v}}}_{2}}$.

2. ФОРМУЛИРОВКА ОСНОВНОГО РЕЗУЛЬТАТА

Основным результатом данной работы является следующая

Теорема 1. Пусть ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$ и пусть подпространство l₁порождено вектором $(1,\alpha ,\beta ,\gamma )$. Пусть $K = \mathbb{Q}(\alpha ,\beta ,\gamma )$ и ${{\sigma }_{1}}( = {\text{id}}),$ ${{\sigma }_{2}},\;{{\sigma }_{3}},\;{{\sigma }_{4}}$ – все вложения поля K в $\mathbb{R}$ (см. предложение 1). Тогда ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ имеет собственную палиндромическую симметрию в том и только в том случае, если (с точностью до перестановки индексов) выполняется

и существуют такие алгебраические числа $\omega $ и $\psi $ степени 4, принадлежащие полю K, что выполнено хотя бы одно из следующих условий:

(1) $(1,\alpha ,\beta ,\gamma ) \sim (1,\omega ,\psi ,\omega {\kern 1pt} ')$: $\psi + \psi {\kern 1pt} ' = - (\omega + \omega {\kern 1pt} ')$;

(2) $(1,\alpha ,\beta ,\gamma ) \sim (1,\omega ,\psi ,\omega {\kern 1pt} ')$: $\psi + \psi {\kern 1pt} ' = 1 - (\omega + \omega {\kern 1pt} ')$;

(3) $(1,\alpha ,\beta ,\gamma ) \sim (1,\omega ,\psi ,\omega {\kern 1pt} ')$: $\psi + \psi {\kern 1pt} ' = 2 - (\omega + \omega {\kern 1pt} ')$;

(4) $(1,\alpha ,\beta ,\gamma )\, \sim \,\left( {1,\omega ,\psi ,\frac{{\omega \, + \,\omega {\kern 1pt} '}}{2}} \right)$: $\psi \, + \,\psi {\kern 1pt} ' = - (\omega \, + \,\omega {\kern 1pt} ')$;

(5) $(1,\alpha ,\beta ,\gamma )\, \sim \,\left( {1,\omega ,\psi ,\frac{{\omega \, + \,\omega {\kern 1pt} '}}{2}} \right)$: $\psi \, + \,\psi {\kern 1pt} '\, = \,2\, - \,(\omega \, + \,\omega {\kern 1pt} ')$;

  (6) $(1,\alpha ,\beta ,\gamma )\, \sim \,\left( {1,\omega ,\psi ,\frac{{\omega \, + \,\omega {\kern 1pt} '\, + \,1}}{2}} \right)$: $\psi \, + \,\psi {\kern 1pt} '\, = \, - {\kern 1pt} (\omega \, + \,\omega {\kern 1pt} ')$;

 (7) $(1,\alpha ,\beta ,\gamma )\, \sim \,\left( {1,\omega ,\psi ,\frac{{\omega \, + \,\omega {\kern 1pt} '\, + \,1}}{2}} \right)$: $\psi \, + \,\psi {\kern 1pt} '\, = \,2\, - \,(\omega \, + \,\omega {\kern 1pt} ')$;

(8) $(1,\alpha ,\beta ,\gamma )\, \sim \,\left( {1,\omega ,\psi ,\frac{{\omega \, + \,\omega {\kern 1pt} '}}{2}} \right)$: $\psi \, + \,\psi {\kern 1pt} '\, = \,1\, - \,\frac{{\omega \, + \,\omega {\kern 1pt} '}}{2}$;

(9) $(1,\alpha ,\beta ,\gamma )\, \sim \,\left( {1,\omega ,\psi ,\frac{{\omega \, + \,\omega {\kern 1pt} '}}{2}} \right)$: $\psi \, + \,\psi {\kern 1pt} '\, = \,2\, - \,\frac{{\omega \, + \,\omega {\kern 1pt} '}}{2}$;

(10) $(1,\alpha ,\beta ,\gamma )\, \sim \,\left( {1,\omega ,\psi ,\frac{{\omega {\kern 1pt} '\, - \,\omega }}{4}} \right)$: $\psi \, + \,\psi {\kern 1pt} '\, = \,2\, - \,\frac{{\omega \, + \,\omega {\kern 1pt} '}}{2}$, где $\omega {\kern 1pt} ' = {{\sigma }_{3}}(\omega ),$ $\psi {\kern 1pt} ' = {{\sigma }_{3}}(\psi )$.

В работе [11] исследуются циклические симметрии, т.е. такие симметрии ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$, которые циклически переставляют направления ${{l}_{1}},\;{{l}_{2}},\;{{l}_{3}},\;{{l}_{4}}$. А именно, в этой работе доказывается, что цепная дробь ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$ имеет собственную циклическую симметрию тогда и только тогда, когда $K$ – циклическое расширение Галуа, ${\text{Gal}}(K{\text{/}}\mathbb{Q}) = \langle {{\sigma }_{2}}\rangle $ и выполняется один из пунктов (1)–(7) теоремы 1 для $\psi = {{\sigma }_{2}}(\omega )$. Следующее утверждение показывает, что не всякая палиндромичная цепная дробь обладает собственными циклическими симметриями:

Предложение 4. Существуют такие вещественные числа $\alpha $, $\beta $, $\gamma $, что подпространство l₁ порождено вектором $(1,\alpha ,\beta ,\gamma )$, вполне вещественное расширение $K = \mathbb{Q}(\alpha ,\beta ,\gamma )$ поля $\mathbb{Q}$ не является нормальным и ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$ – палиндромичная цепная дробь, не обладающая собственными циклическими симметриями.

Любопытно, что критерий наличия собственных циклических симметрий не следует непосредственно из теоремы 1. В связи с этим возникает естественный

Вопрос. Верно ли, что существует такая палиндромичная алгебраическая цепная дробь ${\text{CF}}({{l}_{1}},{{l}_{2}}$, l₃, l₄), для которой поле K является циклическим расширением Галуа и у которой не существует собственных циклических палиндромических симметрий?

Оставшаяся часть статьи имеет следующую структуру: в параграфе 3 мы анализируем то, как у собственных симметрий трехмерных цепных дробей устроены собственные подпространства и перестановки из соотношения (1.1); в параграфе 4 мы изучаем геометрию трехмерных цепных дробей, обладающих собственными симметриями; в параграфе 5 мы устанавливаем связь между определенными классами цепных дробей и матрицами их собственных симметрий; параграф 6 посвящен доказательству теоремы 1; наконец, в параграфе 7 мы доказываем предложение 4.

3. СОБСТВЕННЫЕ СИММЕТРИИ И СОБСТВЕННЫЕ ПОДПРОСТРАНСТВА

Если задана дробь ${\text{CF}}({{l}_{1}}, \ldots ,{{l}_{n}}) = {\text{CF}}(A) \in {{\mathfrak{A}}_{{n - 1}}}$, будем считать, что подпространство l₁ порождается вектором ${{{\mathbf{l}}}_{1}} = (1,{{\alpha }_{1}}, \ldots ,{{\alpha }_{{n - 1}}})$ (данное допущение корректно в силу предложения 1). Тогда из предложения 1 следует, что числа $1,{{\alpha }_{1}}, \ldots ,{{\alpha }_{{n - 1}}}$ образуют базис поля $K = \mathbb{Q}({{\alpha }_{1}}, \ldots ,{{\alpha }_{{n - 1}}})$ над $\mathbb{Q}$ и каждое l_i порождается вектором l_i = $(1,{{\sigma }_{i}}({{\alpha }_{1}}), \ldots ,{{\sigma }_{i}}({{\alpha }_{{n - 1}}}))$, где ${{\sigma }_{1}}( = {\text{id}}),{{\sigma }_{2}}, \ldots ,{{\sigma }_{n}}$ – все вложения K в $\mathbb{R}$. Заметим, что верна следующая

Лемма 3.1. Пусть $G \in {\text{Sy}}{{{\text{m}}}_{\mathbb{Z}}}({\text{CF}}(A))$ и CF(A) = = ${\text{CF}}({{l}_{1}}, \ldots ,{{l}_{n}})$. Пусть $G \ne \pm {{I}_{n}}$ и $G({{{\mathbf{l}}}_{1}}) = \lambda {{{\mathbf{l}}}_{1}}$. Тогда $\lambda \notin \mathbb{Q}$.

Доказательство. Предположим, что $\lambda \in \mathbb{Q}$. Поскольку $G \in {\text{G}}{{{\text{L}}}_{n}}(\mathbb{Z})$ и $G \ne \pm {{I}_{n}}$, то ${\text{rank}}(G - \lambda {{I}_{n}}) > 0$. Так как $(G - \lambda {{I}_{n}})({{{\mathbf{l}}}_{1}}) = {\mathbf{0}}$, то какие-то числа из набора 1, ${{\alpha }_{1}}, \ldots ,{{\alpha }_{{n - 1}}}$ выражаются через оставшиеся числа этого набора в виде некоторой линейной комбинации с коэффициентами из $\mathbb{Q}$. В силу предложения 1 получаем противоречие. □

Отныне будем считать, что n = 4, т.е. будем рассматривать трехмерные цепные дроби. Напомним также, что для каждого $G \in {\text{Sy}}{{{\text{m}}}_{\mathbb{Z}}}({\text{CF}}(A))$ соотношением (1.1) определена перестановка ${{\sigma }_{G}}$.

Лемма 3.2. Пусть G – палиндромическая симметрия ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$, ассоциированной с (гиперболическим) оператором A. Тогда существует такая нумерация подпространств ${{l}_{1}},\;{{l}_{2}},\;{{l}_{3}},\;{{l}_{4}}$, что ${{\sigma }_{G}} = (1,2)(3,4)$ или ${{\sigma }_{G}} = (1,2,3,4)$.

Доказательство. Случай ${{\sigma }_{G}} = {\text{id}}$ невозможен в силу того, что оператор $G$ не является симметрией Дирихле ${\text{CF}}(A)$.

Предположим, существует такая нумерация подпространств ${{l}_{1}},\;{{l}_{2}},\;{{l}_{3}},\;{{l}_{4}}$, что ${{\sigma }_{G}} = (1)(2,3,4)$. Таким образом, существуют такие вещественные числа ${{\mu }_{1}}$, ${{\mu }_{2}}$, ${{\mu }_{3}}$, ${{\mu }_{4}}$, что матрица оператора G в базисе ${{{\mathbf{l}}}_{1}},\;{{{\mathbf{l}}}_{2}},\;{{{\mathbf{l}}}_{3}},\;{{{\mathbf{l}}}_{4}}$ имеет вид

Тогда характеристический многочлен оператора G имеет вид

Следовательно, ${{\mu }_{1}}$ – целое число, и при этом ${{\mu }_{1}}$ – корень уравнения ${{\chi }_{G}}(x) = 0$, т.е. ${{\mu }_{1}} = \pm 1$. Стало быть, l₁ – собственное подпространство оператора G, соответствующее собственному значению ${{\mu }_{1}} = \pm 1$. То есть l₁ рационально, что противоречит гиперболичности оператора A.

Предположим, существует такая нумерация подпространств ${{l}_{1}},\;{{l}_{2}},\;{{l}_{3}},\;{{l}_{4}}$, что ${{\sigma }_{G}} = (1)(2)(3,4)$. Таким образом, существуют такие вещественные числа ${{\mu }_{1}}$, ${{\mu }_{2}}$, ${{\mu }_{3}}$, ${{\mu }_{4}}$, что матрица оператора G в базисе ${{{\mathbf{l}}}_{1}},\;{{{\mathbf{l}}}_{2}},\;{{{\mathbf{l}}}_{3}},\;{{{\mathbf{l}}}_{4}}$ имеет вид

Тогда характеристический многочлен оператора G, коэффициенты которого целочисленны, имеет вид

Так как ${{\mu }_{1}} + {{\mu }_{2}} \in \mathbb{Z}$, то ${{\mu }_{3}}{{\mu }_{4}} \in \mathbb{Q}$. Тогда существуют такие взаимно-простые целые числа $p \geqslant 1$ и $q \geqslant 1$, что ${\text{|}}{{\mu }_{3}}{{\mu }_{4}}{\text{|}} = \frac{p}{q}$, ${\text{|}}{{\mu }_{1}}{{\mu }_{2}}{\text{|}} = \frac{q}{p}$, а значит

Итак, p² делится на q и q² делится на p, т.е. $p = q = 1$ и ${{\mu }_{3}}{{\mu }_{4}} = \pm 1$. Таким образом, матрица оператора G² в базисе ${{{\mathbf{l}}}_{1}},\;{{{\mathbf{l}}}_{2}},\;{{{\mathbf{l}}}_{3}},\;{{{\mathbf{l}}}_{4}}$ имеет вид

Из леммы 3.1 следует, что ${{G}^{2}} = {{I}_{4}}$, т.е. ${{\mu }_{1}} = \pm 1$. Вновь применяя лемму 3.1, получаем, что $G = \pm {{I}_{4}}$, чего не может быть.

Таким образом, существует такая нумерация подпространств ${{l}_{1}},\;{{l}_{2}},\;{{l}_{3}},\;{{l}_{4}}$, что ${{\sigma }_{G}} = (1,2)(3,4)$ или ${{\sigma }_{G}} = (1,2,3,4)$. □

Следствие 1. Пусть $G$ – палиндромическия симметрия ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$. Пусть $G{\kern 1pt} ' = {{G}^{2}}$, если ${\text{ord}}({{\sigma }_{G}}) = 4$, и $G{\kern 1pt} ' = G$, если ${\text{ord}}({{\sigma }_{G}}) = 2$. Тогда $G{\kern 1pt} '$ – палиндромическия симметрия ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ и ${\text{ord}}({{\sigma }_{{G'}}}) = 2$.

Пусть G – палиндромическия симметрия ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$. Изменив при необходимости нумерацию подпространств ${{l}_{1}},\;{{l}_{2}},\;{{l}_{3}},\;{{l}_{4}}$, в силу леммы 3.2 можно рассмотреть такие вещественные числа ${{\mu }_{1}}$, ${{\mu }_{2}}$, ${{\mu }_{3}}$, ${{\mu }_{4}}$, что матрица оператора G в базисе ${{{\mathbf{l}}}_{1}},\;{{{\mathbf{l}}}_{2}},\;{{{\mathbf{l}}}_{3}},\;{{{\mathbf{l}}}_{4}}$ имеет вид

или вид

Пусть G – палиндромическая симметрия ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$ и матрица оператора G в базисе ${{{\mathbf{l}}}_{1}},\;{{{\mathbf{l}}}_{2}},\;{{{\mathbf{l}}}_{3}},\;{{{\mathbf{l}}}_{4}}$ имеет вид (3.1). В работе [11] доказывается, что $G$ является собственной симметрией CF(l₁, ${{l}_{2}},{{l}_{3}},{{l}_{4}})$ тогда и только тогда, когда ${{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}{{\mu }_{4}}$ = 1 (см. следствие 1 в [11]). Для палиндромических симметрий вида (3.2) справедливо аналогичное утверждение:

Лемма 3.3. Пусть $G$ – палиндромическая симметрия ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$ и матрица оператора $G$ в базисе ${{{\mathbf{l}}}_{1}},\;{{{\mathbf{l}}}_{2}},\;{{{\mathbf{l}}}_{3}},\;{{{\mathbf{l}}}_{4}}$ имеет вид (3.2). Тогда $G$ является собственной симметрией дроби ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ в том и только том случае, если ${{\mu }_{1}}{{\mu }_{3}} = {{\mu }_{2}}{{\mu }_{4}} = 1$.

Доказательство. Пусть G является собственной симметрией цепной дроби ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$. Тогда существуют такие числа ${{\varepsilon }_{1}}$, ${{\varepsilon }_{2}}$, ${{\varepsilon }_{3}}$, ${{\varepsilon }_{4}}$ из множества $\{ - 1,1\} $, что

и выполняются неравенства

Стало быть, ${{\mu }_{1}}{{\mu }_{3}} > 0$ и ${{\mu }_{2}}{{\mu }_{4}} > 0$. Так как у оператора G существует неподвижная точка на некотором парусе, то у оператора G существует одномерное собственное подпространство, соответствующее собственному значению 1. Теперь, поскольку характеристический многочлен оператора G имеет вид $({{x}^{2}} - {{\mu }_{1}}{{\mu }_{3}})({{x}^{2}} - {{\mu }_{2}}{{\mu }_{4}})$, то ${{\mu }_{1}}{{\mu }_{3}} = 1$ или ${{\mu }_{2}}{{\mu }_{4}}$ = 1. Тогда ${{\mu }_{1}}{{\mu }_{3}} = {{\mu }_{2}}{{\mu }_{4}} = 1$.

Если ${{\mu }_{1}}{{\mu }_{3}} = {{\mu }_{2}}{{\mu }_{4}} = 1$, то, опять же, характеристический многочлен оператора G имеет вид ${{x}^{4}} - 2{{x}^{2}} + 1$. Стало быть, у оператора G существует целочисленный собственный вектор, соответствующий собственному значению 1. Этот вектор лежит внутри некоторого конуса $C \in \mathcal{C}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$, поскольку цепная дробь ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ является алгебраической. □

Следствие 2. Пусть G – палиндромическия симметрия ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$. Тогда G является собственной симметрией в том и только том случае, если $G{\kern 1pt} '$ (см. следствие 1) является собственной симметрией.

Доказательство. Если G является собственной симметрией ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$, то, очевидно, оператор $G{\kern 1pt} '$ также является собственной симметрией цепной дроби ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$.

Обратно, предположим $G{\kern 1pt} '$ – собственная симметрия ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$. Если ${\text{ord}}({{\sigma }_{G}}) = 4$, то, изменив при необходимости нумерацию подпространств ${{l}_{1}},\;{{l}_{2}},\;{{l}_{3}},\;{{l}_{4}}$, можно считать, что матрица оператора G в базисе ${{{\mathbf{l}}}_{1}},\;{{{\mathbf{l}}}_{2}},\;{{{\mathbf{l}}}_{3}},\;{{{\mathbf{l}}}_{4}}$ имеет вид (3.2). Тогда матрица оператора $G{\kern 1pt} ' = {{G}^{2}}$ в базисе ${{{\mathbf{l}}}_{1}},\;{{{\mathbf{l}}}_{2}},\;{{{\mathbf{l}}}_{3}},\;{{{\mathbf{l}}}_{4}}$ имеет вид

Стало быть, в силу леммы 3.3 ${{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}{{\mu }_{4}} = 1$, а значит G – собственная симметрия цепной дроби ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ (см. следствие 1 в [11]). □

Лемма 3.4. Пусть G – собственная симметрия ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$ и ${\text{ord}}({{\sigma }_{G}}) = 2$. Тогда существуют такие одномерные рациональные подпространства $l_{ + }^{1}$, $l_{ + }^{2}$, $l_{ - }^{1}$ и $l_{ - }^{2}$, что $Gl_{ + }^{1} = l_{ + }^{1}$, $Gl_{ + }^{2} = l_{ + }^{2}$, $Gl_{ - }^{1} = l_{ - }^{1}$, $Gl_{ - }^{2} = l_{ - }^{2}$ и $l_{ + }^{1} + l_{ + }^{2} + l_{ - }^{1} + l_{ - }^{2} = {{\mathbb{R}}^{4}}$. При этом подпространства $l_{ + }^{1}$ и $l_{ + }^{2}$ соответствуют собственному значению 1, а подпространства $l_{ - }^{1}$ и $l_{ - }^{2}$ соответствуют собственному значению –1.

Доказательство. Изменив при необходимости нумерацию подпространств ${{l}_{1}},\;{{l}_{2}},\;{{l}_{3}},\;{{l}_{4}}$, в силу леммы 3.3 можно считать, что существуют такие вещественные числа ${{\mu }_{1}}$ и ${{\mu }_{2}}$, что матрица оператора G в базисе ${{{\mathbf{l}}}_{1}},\;{{{\mathbf{l}}}_{2}},\;{{{\mathbf{l}}}_{3}},\;{{{\mathbf{l}}}_{4}}$ имеет вид

Так как ${{\chi }_{G}}(x) = (x - {{1)}^{2}}{{(x + 1)}^{2}}$, то у оператора G есть двумерное инвариантное подпространство ${{L}_{ + }}$, соответствующее собственному значению 1, и двумерное инвариантное подпространство ${{L}_{ - }}$, соответствующее собственному значению –1. Покажем рациональность подпространств ${{L}_{ + }}$ и ${{L}_{ - }}$, из чего будет следовать утверждение леммы.

Поскольку подпространство ${{L}_{ + }}$ совпадает с решением системы линейных уравнений

то фундаментальная система решений данной системы линейных уравнений имеет размерность 2. Рассмотрев в качестве значений свободных переменных наборы (0, 1) и (1, 0), мы определим два линейно-независимых рациональных решения данной системы, из чего следует рациональность ${{L}_{ + }}$. Рациональность подпространства ${{L}_{ - }}$ доказывается аналогичным способом. □

4. ГЕОМЕТРИЯ СОБСТВЕННЫХ СИММЕТРИЙ

Лемма 4.1. Пусть $G$ – собственная симметрия дроби ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$. Пусть $F = G{\kern 1pt} '$ (см. следствие 1) – собственная симметрия ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ (см. следствие 2). Тогда существуют ${{{\mathbf{z}}}_{1}},{{{\mathbf{z}}}_{2}},{{{\mathbf{z}}}_{3}},{{{\mathbf{z}}}_{4}} \in {{\mathbb{Z}}^{4}}$, такие что

и выполняется хотя бы одно из следующих одиннадцати утверждений:

(1) вектора ${{{\mathbf{z}}}_{1}}$, ${{{\mathbf{z}}}_{2}}$, ${{{\mathbf{z}}}_{3}}$, $\frac{1}{4}({{{\mathbf{z}}}_{1}} + {{{\mathbf{z}}}_{2}} + {{{\mathbf{z}}}_{3}} + {{{\mathbf{z}}}_{4}})$ образуют базис решетки ${{\mathbb{Z}}^{4}}$;

(2) вектора ${{{\mathbf{z}}}_{1}}$, ${{{\mathbf{z}}}_{2}}$, ${{{\mathbf{z}}}_{3}}$, ${{{\mathbf{z}}}_{4}}$ образуют базис решетки ${{\mathbb{Z}}^{4}}$;

(3) вектора ${{{\mathbf{z}}}_{1}}$, $\frac{1}{2}({{{\mathbf{z}}}_{1}} + {{{\mathbf{z}}}_{2}})$, $\frac{1}{2}({{{\mathbf{z}}}_{1}} + {{{\mathbf{z}}}_{3}})$, $\frac{1}{2}({{{\mathbf{z}}}_{1}} + {{{\mathbf{z}}}_{4}})$ образуют базис решетки ${{\mathbb{Z}}^{4}}$;

(4) вектора ${{{\mathbf{z}}}_{1}}$, ${{{\mathbf{z}}}_{2}}$, $\frac{1}{2}({{{\mathbf{z}}}_{1}} + {{{\mathbf{z}}}_{3}})$, $\frac{1}{4}({{{\mathbf{z}}}_{1}} + {{{\mathbf{z}}}_{2}} + {{{\mathbf{z}}}_{3}} + {{{\mathbf{z}}}_{4}})$ образуют базис решетки ${{\mathbb{Z}}^{4}}$;

(5) вектора ${{{\mathbf{z}}}_{1}}$, ${{{\mathbf{z}}}_{2}}$, $\frac{1}{2}({{{\mathbf{z}}}_{1}} + {{{\mathbf{z}}}_{3}})$, $\frac{1}{2}({{{\mathbf{z}}}_{2}} + {{{\mathbf{z}}}_{4}})$ образуют базис решетки ${{\mathbb{Z}}^{4}}$;

(6) вектора ${{{\mathbf{z}}}_{1}}$, ${{{\mathbf{z}}}_{2}}$, ${{{\mathbf{z}}}_{3}}$, $\frac{1}{2}({{{\mathbf{z}}}_{1}} + {{{\mathbf{z}}}_{3}} + {{{\mathbf{z}}}_{4}} - {{{\mathbf{z}}}_{2}})$ образуют базис решетки ${{\mathbb{Z}}^{4}}$;

(7) вектора ${{{\mathbf{z}}}_{1}}$, ${{{\mathbf{z}}}_{2}}$, ${{{\mathbf{z}}}_{3}}$, $\frac{1}{2}({{{\mathbf{z}}}_{1}}\, + \,{{{\mathbf{z}}}_{2}})\, + \,\frac{1}{4}({{{\mathbf{z}}}_{1}}\, + \,{{{\mathbf{z}}}_{4}}\, - \,{{{\mathbf{z}}}_{3}}$ – z₂) образуют базис решетки ${{\mathbb{Z}}^{4}}$;

(8) вектора ${{{\mathbf{z}}}_{1}}$, ${{{\mathbf{z}}}_{2}}$, ${{{\mathbf{z}}}_{3}}$, $\frac{1}{2}({{{\mathbf{z}}}_{2}} + {{{\mathbf{z}}}_{4}})$ образуют базис решетки ${{\mathbb{Z}}^{4}}$;

(9) вектора ${{{\mathbf{z}}}_{1}}$, ${{{\mathbf{z}}}_{2}}$, $\frac{1}{2}({{{\mathbf{z}}}_{1}}\, + \,{{{\mathbf{z}}}_{3}})$, $\frac{1}{4}{{{\mathbf{z}}}_{1}}\, + \,\frac{1}{2}{{{\mathbf{z}}}_{2}}\, - \,\frac{1}{4}{{{\mathbf{z}}}_{3}}\, + \,\frac{1}{2}{{{\mathbf{z}}}_{4}}$ образуют базис решетки ${{\mathbb{Z}}^{4}}$;

(10) вектора ${{{\mathbf{z}}}_{1}}$, ${{{\mathbf{z}}}_{2}}$, $\frac{1}{2}({{{\mathbf{z}}}_{1}} + {{{\mathbf{z}}}_{3}})$, $\frac{1}{2}{{{\mathbf{z}}}_{1}} + \frac{1}{4}{{{\mathbf{z}}}_{2}} + \frac{1}{2}{{{\mathbf{z}}}_{4}}$ образуют базис решетки ${{\mathbb{Z}}^{4}}$;

(11) вектора ${{{\mathbf{z}}}_{1}}$, $\frac{1}{2}({{{\mathbf{z}}}_{1}} + {{{\mathbf{z}}}_{2}})$, ${{{\mathbf{z}}}_{3}}$, $\frac{1}{2}({{{\mathbf{z}}}_{1}} + {{{\mathbf{z}}}_{3}} + {{{\mathbf{z}}}_{4}} - {{{\mathbf{z}}}_{2}})$ образуют базис решетки ${{\mathbb{Z}}^{4}}$.

Доказательство. Будем называть плоскость рациональной, если множество содержащихся в нем целых точек является (аффинной) решеткой ранга, равного размерности этой плоскости.

Рассмотрим для собственной симметрии F подпространства $l_{ + }^{1}$, $l_{ + }^{2}$, $l_{ - }^{1}$ и $l_{ - }^{2}$ из леммы 3.4 и положим $S = l_{ + }^{2} + l_{ - }^{1} + l_{ - }^{2}$. Обозначим через ${{S}_{1}}$ ближайшую к $S$ рациональную гиперплоскость, параллельную $S$ и не совпадающую с S (любую из двух). Тогда $G({{S}_{1}}) = {{S}_{1}}$. Также обозначим через p точку пересечения гиперплоскости ${{S}_{1}}$ и $l_{ + }^{1}$, а через $l$ и $\pi $ прямую и плоскость, проходящие через точку p и параллельные $l_{ + }^{2}$ и ${{L}_{ - }} = l_{ - }^{1} + l_{ - }^{2}$ соответственно. При этом $F(l) = l$, $F(\pi ) = \pi $ и $F({\mathbf{p}}) = {\mathbf{p}}$.

Плоскость $\pi $ разделяет гиперплоскость ${{S}_{1}}$ на два множества $S_{1}^{ + }$ и $S_{1}^{ - }$. Пусть $Q$ и R – рациональные плоскости, ближайшие к $\pi $, параллельные $\pi $ и не совпадающие с $\pi $, принадлежащие множествам $S_{1}^{ + }$ и $S_{1}^{ - }$ соответственно. Отметим, что, вообще говоря, расстояния от $\pi $ до Q и от $\pi $ до R не обязательно равны. Положим ${{{\mathbf{p}}}^{Q}} = Q \cap l$ и ${{{\mathbf{p}}}^{R}} = R \cap l$.

Пусть $({{{\mathbf{z}}}_{1}},{{{\mathbf{z}}}_{2}})$ – такая пара точек решетки ${{\mathbb{Z}}^{4}}$, что ${{{\mathbf{z}}}_{1}} \in Q,$ ${{{\mathbf{z}}}_{2}} \in R$, вектора ${{{\mathbf{z}}}_{1}} - {{{\mathbf{p}}}^{Q}}$ и ${{{\mathbf{z}}}_{2}} - {{{\mathbf{p}}}^{R}}$ неколлинеарны. Тогда можно построить точки

Рассмотренные точки определяют тройку параллелограммов $({{\Delta }^{\pi }},{{\Delta }^{Q}},{{\Delta }^{R}})$, где

При помощи метода спуска можно построить такую пару $({{{\mathbf{z}}}_{1}},{{{\mathbf{z}}}_{2}})$, что (см. рис. 1)

и ${{\Delta }^{\pi }} \cap {{\mathbb{Z}}^{4}}$ является подмножеством множества

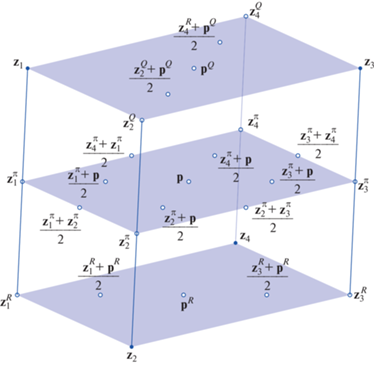
Аккуратно перебирая возможные расположения точек решетки ${{\mathbb{Z}}^{4}}$ в тройке параллелограммов $({{\Delta }^{\pi }},{{\Delta }^{Q}},{{\Delta }^{R}})$, мы попадаем в одну из одиннадцати ситуаций, соответствующей одному из утверждений (1)–(11).

5. МАТРИЦЫ СОБСТВЕННЫХ СИММЕТРИЙ

Напомним, что если задана дробь CF(l₁, l₂, ${{l}_{3}},{{l}_{4}}) = {\text{CF}}(A) \in {{\mathfrak{A}}_{3}}$, будем считать, что подпространство l₁ порождается вектором ${{{\mathbf{l}}}_{1}} = (1,\alpha ,\beta ,\gamma )$. Тогда из предложения 1 следует, что числа 1, $\alpha ,\beta ,\gamma $ образуют базис поля $K = \mathbb{Q}(\alpha ,\beta ,\gamma )$ над $\mathbb{Q}$ и каждое l_i порождается вектором l_i = (1, σ_i(α), ${{\sigma }_{i}}(\beta ),{{\sigma }_{i}}(\gamma ))$, где ${{\sigma }_{1}}( = {\text{id}}),{{\sigma }_{2}},{{\sigma }_{3}},{{\sigma }_{4}}$ – все вложения K в $\mathbb{R}$. То есть, если через $({{{\mathbf{l}}}_{1}},{{{\mathbf{l}}}_{2}},{{{\mathbf{l}}}_{3}},{{{\mathbf{l}}}_{4}})$ обозначить матрицу со столбцами ${{{\mathbf{l}}}_{1}},\;{{{\mathbf{l}}}_{2}},\;{{{\mathbf{l}}}_{3}},\;{{{\mathbf{l}}}_{4}}$, получим

Мы будем обозначать через $\widetilde {{{\mathfrak{A}}_{3}}}$ множество всех трехмерных алгебраических цепных дробей, для которых

Для каждого $i = 1,2, \ldots ,10$ определим ${\mathbf{C}}{{{\mathbf{F}}}_{i}}$ как класс дробей из $\widetilde {{{\mathfrak{A}}_{3}}}$, удовлетворяющих паре соотношений ${{\Re }_{i}}$, где

Покажем, что все дроби из классов ${\mathbf{C}}{{{\mathbf{F}}}_{i}}$, палиндромичны для каждого $i = 1,2, \ldots ,10$. Положим ${{G}_{1}},{{G}_{2}}, \ldots ,{{G}_{{10}}}$ равными соответственно матрицам

Лемма 5.1. Пусть ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$ и $i \in \{ 1,2$, ..., 10}. Тогда цепная дробь ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ принадлежит классу ${\mathbf{C}}{{{\mathbf{F}}}_{i}}$ в том и только в том случае, если ${{G}_{i}}$ – ее собственная симметрия и ${\text{ord}}({{\sigma }_{{{{G}_{i}}}}})$ = 2.

Доказательство. Покажем, что CF(l₁, l₂, ${{l}_{3}},{{l}_{4}})$ принадлежит классу ${\mathbf{C}}{{{\mathbf{F}}}_{1}}$ в том и только в том случае, если ${{G}_{1}}$ – ее собственная симметрия и ${\text{ord}}({{\sigma }_{{{{G}_{1}}}}}) = 2$.

В силу леммы 3.3 оператор $G \in {\text{G}}{{{\text{L}}}_{4}}(\mathbb{Z})$ является собственной симметрией дроби ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ и ${\text{ord}}({{\sigma }_{G}})$ = 2 тогда и только тогда, когда с точностью до перестановки индексов существуют такие действительные числа ${{\mu }_{1}},\;{{\mu }_{2}},\;{{\mu }_{3}},\;{{\mu }_{4}}$, что $G({{{\mathbf{l}}}_{1}},{{{\mathbf{l}}}_{2}},{{{\mathbf{l}}}_{3}},{{{\mathbf{l}}}_{4}})$ = = $({{\mu }_{3}}{{{\mathbf{l}}}_{3}},{{\mu }_{4}}{{{\mathbf{l}}}_{4}},{{\mu }_{1}}{{{\mathbf{l}}}_{1}},{{\mu }_{2}}{{{\mathbf{l}}}_{2}})$ и ${{\mu }_{1}}{{\mu }_{3}} = {{\mu }_{2}}{{\mu }_{4}} = 1$.

Пусть ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {\mathbf{C}}{{{\mathbf{F}}}_{1}}$. Заметим, что σ₂ = = ${{\sigma }_{2}}\sigma _{3}^{2} = {{\sigma }_{4}}{{\sigma }_{3}}$, ${{\sigma }_{2}}(\gamma ) = {{\sigma }_{2}}{{\sigma }_{3}}(\alpha )$, ${{\sigma }_{3}}(\gamma ) = \sigma _{3}^{2}(\alpha ) = \alpha $, ${{\sigma }_{4}}(\gamma ) = {{\sigma }_{4}}{{\sigma }_{3}}(\alpha ) = {{\sigma }_{2}}(\alpha )$, ${{\sigma }_{2}}(\beta ) + {{\sigma }_{2}}{{\sigma }_{3}}(\beta )$  =  ${{\sigma }_{2}}(\beta + $ $ + \,{{\sigma }_{3}}(\beta ))$ = ${{\sigma }_{2}}( - (\alpha + {{\sigma }_{3}}(\alpha )))$ = $ - ({{\sigma }_{2}}(\alpha ) + {{\sigma }_{2}}{{\sigma }_{3}}(\alpha ))$ и ${{\sigma }_{4}}(\beta ) = {{\sigma }_{2}}{{\sigma }_{3}}(\beta )$. Тогда

то есть ${{G}_{{\text{1}}}}({{{\mathbf{l}}}_{1}},{{{\mathbf{l}}}_{2}},{{{\mathbf{l}}}_{3}},{{{\mathbf{l}}}_{4}}) = ({{{\mathbf{l}}}_{3}},{{{\mathbf{l}}}_{4}},{{{\mathbf{l}}}_{1}},{{{\mathbf{l}}}_{2}})$. Следовательно, G₁ – собственная симметрия ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ и ${\text{ord}}({{\sigma }_{{{{G}_{1}}}}}) = 2$. Обратно, предположим, G₁ – собственная симметрия ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ и ${\text{ord}}({{\sigma }_{{{{G}_{1}}}}}) = 2$. Тогда существует ${{\mu }_{3}}$ такое, что с точностью до перестановки индексов

откуда ${{\mu }_{3}}$ = 1, $\gamma = {{\sigma }_{3}}(\alpha )$, $\sigma _{3}^{2}(\alpha ) = {{\sigma }_{3}}(\gamma )$ = α, $\sigma _{3}^{2}(\gamma ) = {{\sigma }_{3}}(\alpha )$ = γ, β + ${{\sigma }_{3}}(\beta ) = - (\alpha + {{\sigma }_{3}}(\alpha ))$, $\sigma _{3}^{2}(\beta )\, = \, - {\kern 1pt} {{\sigma }_{3}}(\beta )\, - \,({{\sigma }_{3}}(\alpha )\, + \,\sigma _{3}^{2}(\alpha ))$ = $ - {{\sigma }_{3}}(\beta )$ – (α + σ₃(α)) = = β.Существует μ₄ такое, что откуда ${{\mu }_{4}} = 1$, ${{\sigma }_{4}}(\alpha ) = {{\sigma }_{2}}(\gamma ) = {{\sigma }_{2}}{{\sigma }_{3}}(\alpha )$, σ₄(γ) = = ${{\sigma }_{2}}(\alpha ) = {{\sigma }_{2}}{{\sigma }_{3}}(\gamma )$, ${{\sigma }_{4}}(\beta )\, = \, - {\kern 1pt} {{\sigma }_{2}}(\beta )\, - \,({{\sigma }_{2}}(\alpha )\, + \,{{\sigma }_{2}}(\gamma ))$ = = ${{\sigma }_{2}}( - \beta - (\alpha + \gamma ))\, = \,{{\sigma }_{2}}{{\sigma }_{3}}(\beta )$. Следовательно, CF(l₁, l₂, ${{l}_{3}},{{l}_{4}}) \in {\mathbf{C}}{{{\mathbf{F}}}_{1}}$, так как числа 1, $\alpha ,\beta ,\gamma $ образуют базис поля $K = \mathbb{Q}(\alpha ,\beta ,\gamma )$.

Для $i = 2, \ldots ,10$ рассуждения аналогичны. □

6. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 1

Обозначим для каждого $i = 1, \ldots ,10$ через ${{\overline {{\mathbf{CF}}} }_{i}}$ образ CF_i при действии группы ${\text{G}}{{{\text{L}}}_{4}}(\mathbb{Z})$:

Лемма 6.1. Для дроби ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$ выполняется условие (i) теоремы 1 тогда и только тогда, когда ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ принадлежит классу ${{\overline {{\mathbf{CF}}} }_{i}}$, где $i \in \{ 1,2, \ldots ,10\} $.

Доказательство. Для любого $X \in {\text{G}}{{{\text{L}}}_{4}}(\mathbb{Z})$ гиперболичность оператора $A \in {\text{G}}{{{\text{L}}}_{4}}(\mathbb{Z})$ равносильна гиперболичности оператора $XA{{X}^{{ - 1}}}$. При этом собственные подпространства гиперболического оператора однозначно восстанавливаются по любому его собственному вектору. Остается воспользоваться определением эквивалентности из параграфа 1. □

Теорему 1 при помощи леммы 6.1 можно переформулировать следующим образом: дробь ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$ имеет собственную симметрию $G$ тогда и только тогда, когда она принадлежит одному из классов ${{\overline {{\mathbf{CF}}} }_{i}}$, где $i \in \{ 1,2, \ldots ,10\} $.

Доказательство теоремы 1. Если ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ принадлежит какому-то ${{\overline {{\mathbf{CF}}} }_{i}}$, то по лемме 5.1 она имеет собственную симметрию $G$, ибо действие оператора из ${\text{G}}{{{\text{L}}}_{4}}(\mathbb{Z})$ сохраняет свойство существования у алгебраической цепной дроби собственной симметрии.

Обратно, пусть дробь ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\mathfrak{A}}_{3}}$ имеет собственную симметрию $G$. Положим $F = G'$ и рассмотрим точки ${{{\mathbf{z}}}_{1}}$, ${{{\mathbf{z}}}_{2}}$, ${{{\mathbf{z}}}_{3}}$, ${{{\mathbf{z}}}_{4}}$ из леммы 4.1. Обозначим также через ${{{\mathbf{e}}}_{1}}$, ${{{\mathbf{e}}}_{2}}$, ${{{\mathbf{e}}}_{3}}$, ${{{\mathbf{e}}}_{4}}$ стандартный базис ${{\mathbb{R}}^{4}}$. Для точек ${{{\mathbf{z}}}_{1}}$, ${{{\mathbf{z}}}_{2}}$, ${{{\mathbf{z}}}_{3}}$, ${{{\mathbf{z}}}_{4}}$ выполняется хотя бы одно из утверждений (1)–(11) леммы 4.1.

Пусть выполняется утверждение (1) леммы 4.1. Рассмотрим такой оператор ${{X}_{1}} \in {\text{G}}{{{\text{L}}}_{4}}(\mathbb{Z})$, что

Тогда ${{X}_{1}}({{{\mathbf{z}}}_{4}})$ = ${{X}_{1}}\left( {4\, \cdot \,\frac{1}{4}({{{\mathbf{z}}}_{1}}\, + \,{{{\mathbf{z}}}_{2}}\, + \,{{{\mathbf{z}}}_{3}}\, + \,{{{\mathbf{z}}}_{4}})\, - \,{{{\mathbf{z}}}_{1}}\, - \,{{{\mathbf{z}}}_{2}}\, - \,{{{\mathbf{z}}}_{3}}} \right)$ = = ${{{\mathbf{e}}}_{1}} + {{{\mathbf{e}}}_{2}} - {{{\mathbf{e}}}_{3}}$ и ${{X}_{1}}GX_{1}^{{ - 1}} = {{G}_{1}}$, так как по лемме 4.1

Стало быть, ${{X}_{1}}({\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})) \in {\mathbf{C}}{{{\mathbf{F}}}_{1}}$, т.е. ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\overline {{\mathbf{CF}}} }_{1}}$.

Рассуждения аналогичны для случаев, когда выполняется утверждение (i) леммы 4.1, где $i = 2, \ldots ,10$.

Если выполняется утверждение (11) леммы 4.1, то, как и при выполнении утверждения (2) леммы 4.1, вновь ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\overline {{\mathbf{CF}}} }_{2}}$. Действительно, пусть выполняется утверждение (11) леммы 4.1. Рассмотрим такой оператор ${{X}_{{11}}} \in {\text{G}}{{{\text{L}}}_{4}}(\mathbb{Z})$, что

Тогда X₁₁(z₂) = ${{X}_{{11}}}\left( {2 \cdot \frac{1}{2}({{{\mathbf{z}}}_{1}}\, + \,{{{\mathbf{z}}}_{2}})\, - \,{{{\mathbf{z}}}_{1}}} \right)\, = \,{{{\mathbf{e}}}_{1}} + 2{{{\mathbf{e}}}_{4}}$, ${{X}_{{11}}}({{{\mathbf{z}}}_{4}})$ = X₁₁$\left( {2 \cdot \frac{1}{2}({{{\mathbf{z}}}_{1}} - {{{\mathbf{z}}}_{2}} + {{{\mathbf{z}}}_{3}} + {{{\mathbf{z}}}_{4}}) - {{{\mathbf{z}}}_{1}} + {{{\mathbf{z}}}_{2}} - {{{\mathbf{z}}}_{3}}} \right)$ = = ${{{\mathbf{e}}}_{1}} + 2{{{\mathbf{e}}}_{2}} - {{{\mathbf{e}}}_{3}}$ и ${{X}_{{11}}}GX_{{11}}^{{ - 1}} = {{G}_{2}}$, так как по лемме 4.1

Стало быть, ${{X}_{{11}}}({\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})) \in {\mathbf{C}}{{{\mathbf{F}}}_{2}}$, т.е. ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in {{\overline {{\mathbf{CF}}} }_{2}}$. □

7. ПРИМЕР ПАЛИНДРОМИЧНОЙ ЦЕПНОЙ ДРОБИ, НЕ ОБЛАДАЮЩЕЙ СОБСТВЕННЫМИ ЦИКЛИЧЕСКИМИ СИММЕТРИЯМИ

Рассмотрим вещественные числа ${{\theta }_{1}} = \sqrt {4 + \sqrt 2 } $ и ${{\theta }_{2}} = \sqrt {4 - \sqrt 2 } $. Заметим, что $\theta _{1}^{2} = 4 + \sqrt 2 $, а значит ${{\theta }_{1}}$ является корнем уравнения ${{x}^{4}} - 8{{x}^{2}} + 14 = 0$. В силу критерия Эйзенштейна для p = 2 многочлен $f(x) = {{x}^{4}} - 8{{x}^{2}} + 14$ неприводим над $\mathbb{Q}$. Таким образом, f(x) – минимальный многочлен для ${{\theta }_{1}}$ и

Рассмотрим такие вложения ${{\sigma }_{1}},\;{{\sigma }_{2}},\;{{\sigma }_{3}},\;{{\sigma }_{4}}$ вполне вещественного поля $\mathbb{Q}({{\theta }_{1}})$, что ${{\sigma }_{1}}({{\theta }_{1}}) = {{\theta }_{1}}$, ${{\sigma }_{2}}({{\theta }_{1}})$ = = θ₂, ${{\sigma }_{3}}({{\theta }_{1}}) = - {{\theta }_{1}}$, ${{\sigma }_{4}}({{\theta }_{1}}) = - {{\theta }_{2}}$. Пусть ${{K}_{1}} = \mathbb{Q}({{\theta }_{1}})$, ${{K}_{2}} = \mathbb{Q}({{\theta }_{2}})$, ${{K}_{3}} = \mathbb{Q}( - {{\theta }_{1}})$, ${{K}_{4}} = \mathbb{Q}( - {{\theta }_{2}})$ – сопряженные поля над $\mathbb{Q}$. Ясно, что ${{K}_{1}} = {{K}_{3}}$, ${{K}_{2}} = {{K}_{4}}$ и $\sigma _{3}^{2} = {\text{id}}$, ${{\sigma }_{4}} = {{\sigma }_{2}}{{\sigma }_{3}}$.

Предположим, что ${{K}_{1}} = {{K}_{2}}$. Поскольку (x – ‒ θ₁)$(x + {{\theta }_{1}}) = {{x}^{2}} - 4 - \sqrt 2 \in \mathbb{Q}(\sqrt 2 )[x]$, то ${{K}_{1}}$ – нормальное расширение степени 2 поля $\mathbb{Q}(\sqrt 2 )$. При этом $(x - {{\theta }_{2}})(x + {{\theta }_{2}})$ = ${{x}^{2}} - 4 + \sqrt 2 \in \mathbb{Q}(\sqrt 2 )[x]$. Пусть $\phi \, \in \,{\text{Gal}}({{K}_{1}}{\text{/}}\mathbb{Q}(\sqrt 2 ))$. Тогда ϕ(θ₁θ₂) = $( - {{\theta }_{1}})( - {{\theta }_{2}})$ = = θ₁θ₂, а значит ${{\theta }_{1}}{{\theta }_{2}} = \sqrt {14} \in \mathbb{Q}(\sqrt 2 )$, чего не может быть. Таким образом, ${{K}_{1}} \ne {{K}_{2}}$.

Поскольку $\theta = {{\theta }_{1}}$ – примитивный элемент расширения ${{K}_{1}}$, то набор чисел 1, $\theta ,{{\theta }^{2}},{{\theta }^{3}}$ является базисом K₁. Положим $\omega = \theta + {{\theta }^{2}}$ и $\psi = - {{\theta }^{2}} + \frac{1}{2}{{\theta }^{3}}$. Тогда $\omega {\kern 1pt} '{\kern 1pt} ' = {{\sigma }_{3}}(\omega ) = - \theta \, + \,{{\theta }^{2}}$, $\psi {\kern 1pt} '{\kern 1pt} '\, = \,{{\sigma }_{3}}(\psi )\, = \, - {{\theta }^{2}}\, - \,\frac{1}{2}{{\theta }^{3}}$. Заметим, что $\psi + \psi {\kern 1pt} '{\kern 1pt} ' = - 2{{\theta }^{2}} = - (\omega + \omega {\kern 1pt} '{\kern 1pt} ')$ и набор чисел 1, $\omega $, $\psi $, $\omega {\kern 1pt} '{\kern 1pt} '$ является базисом ${{K}_{1}}$, поскольку

Теперь, полагая, что $\alpha = \omega $, $\beta = \psi $, $\gamma = \omega {\kern 1pt} '{\kern 1pt} '$, с помощью предложения 1 можно построить алгебраическую цепную дробь ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}}) \in \widetilde {{{\mathfrak{A}}_{3}}}$, где подпространство l₁ порождено вектором (1, α, $\beta ,\gamma )$. Поскольку выполняется утверждение (1) теоремы 1, то ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ – палиндромичная цепная дробь. При этом, поскольку ${{K}_{1}} \ne {{K}_{2}}$, то ${\text{CF}}({{l}_{1}},{{l}_{2}},{{l}_{3}},{{l}_{4}})$ не обладает циклическими симметриями (см. работу [11]).