1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 507, № 1, 2022

Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 507, № 1, стр. 51-56

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ АКУСТИЧЕСКИХ ПРОЦЕССОВ В ГРАДИЕНТНЫХ СРЕДАХ СЕТОЧНО-ХАРАКТЕРИСТИЧЕСКИМ МЕТОДОМ

Член-корреспондент РАН И. Б. Петров 1, *, В. И. Голубев 1, **, Ю. С. Анкипович 2, ***, А. В. Фаворская 1, ****

1 Научно-исследовательский институт системных исследований Российской академии наук
Москва, Россия

2 Московский физико-технический институт (национальный исследовательский университет)
Долгопрудный, Московская обл., Россия

* E-mail: petrov@mipt.ru
** E-mail: w.golubev@mail.rugolubev.vi@mipt.ru
*** E-mail: ankipovich.ius@phystech.edu
**** E-mail: aleanera@yandex.ru

Поступила в редакцию 05.08.2022
После доработки 24.10.2022
Принята к публикации 28.10.2022

Полный текст (PDF)

Аннотация

В настоящей работе рассматривается задача распространения сейсмических волн в градиентных геологических средах. Для описания их динамического поведения используются акустическое приближение и процедура численного интегрирования начально-краевой задачи акустического волнового уравнения с механическими параметрами, имеющими пространственную изменчивость. Разработан сеточно-характеристический численный метод, явно учитывающий градиентность среды. Проведено сравнение полученных численных решений с результатами расчетов при аппроксимации среды кусочно-постоянной моделью в одномерном случае.

Ключевые слова: градиентные среды, акустика, математическое моделирование, сеточно-характеристический метод

1. ВВЕДЕНИЕ

Для математического моделирования процесса распространения сейсмических волн в геологических средах успешно применяется система уравнений линейной акустики [1, 2]. Для численного решения определяющей системы уравнений применяются различные численные методы: конечно-разностный [3, 4], конечно-объемный [5], метод конечных элементов [6, 7], сеточно-характеристический метод [8–10] и другие. В данной работе используется класс сеточно-характеристических методов, развитый для линейных гиперболических систем.

Изменение механических свойств геологического массива с глубиной вносит вклад в процесс распространения в нем сейсмических волн. Градиентную среду можно приближенно описывать разными вычислительными моделями: считать всю среду однородной с некоторыми средними параметрами, разбить среду на несколько зон, в каждой из которой свойства материала считаются постоянными, явно учитывать градиентность среды на этапе построения расчетного алгоритма. Численное решение системы уравнений линейной акустики для случая постоянных и кусочно-постоянных коэффициентов рассмотрено во множестве работ [11, 12]. Однако работы, которые явно учитывают градиентность среды, редки и, зачастую, в них рассматривается только переменная скорость звука, тогда как плотность среды считается постоянной [13, 14].

В настоящей работе разработан сеточно-характеристический метод, явно учитывающий изменение скорости звука и плотности среды внутри расчетной ячейки. Представлено сравнение волновых полей с результатами, получаемыми в рамках применения модели акустической среды с кусочно-постоянными коэффициентами.

2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И ЧИСЛЕННЫЙ МЕТОД

Система уравнений акустики может быть получена из уравнения неразрывности [15]

(1)
$\frac{{\partial \rho }}{{\partial t}} + {\text{div}}(\rho \vec {V}) = 0$
и уравнения Эйлера
(2)
$\rho \left[ {\frac{{\partial{ \vec {V}}}}{{\partial t}} + \left( {\vec {V} \cdot \nabla } \right)\vec {V}} \right] = - \nabla p$,
где $\rho \left( {\vec {r}} \right)$ – плотность рассматриваемой среды, $p$ – давление, $\vec {V}$ – скорость частиц среды. Для замыкания системы будем использовать предположение о баротропности среды $p = p\left( \rho \right)$. Особенностью данной системы является возможность распространения акустических волн с конечной скоростью $c$, определяемой параметрами среды.

Рассмотрим малые возмущения относительно равновесного состояния, характеризующегося параметрами $\left( {{{\rho }_{0}},{{p}_{0}},{{{\vec {V}}}_{0}}} \right)$, возникающие во время распространения звуковой волны:

(3)
$\begin{array}{*{20}{c}} {\left\{ {\begin{array}{*{20}{l}} {\rho = {{\rho }_{0}}\left( {\vec {r}} \right) + \rho {\kern 1pt} ',} \\ {p = {{p}_{0}} + p{\kern 1pt} ',} \\ {\vec {V} = {{{\vec {V}}}_{0}} + \vec {V}{\kern 1pt} ',} \end{array}} \right.} \\ {\rho {\kern 1pt} ' \ll {{\rho }_{0}},\quad p{\kern 1pt} ' \ll {{p}_{0}},\quad \left| {\vec {V}} \right| \ll c.} \end{array}$

В предположении изначально покоящейся среды $({{\vec {V}}_{0}} = \vec {0})$ получаем линеаризованную систему уравнений [16]:

(4)
$\left\{ {\begin{array}{*{20}{l}} {\frac{{\partial{ \vec {V}}}}{{\partial t}} + \frac{{\nabla p}}{\rho } = \vec {0},} \\ {\frac{{\partial p}}{{\partial t}} + \rho {{c}^{2}}{\text{div}}\vec {V} = 0,} \end{array}} \right.$
где $\rho \left( {\vec {r}} \right)$ – равновесная плотность рассматриваемой среды (для краткости опущен индекс 0), $p$ – отклонение давления от равновесного состояния, $\vec {V}$ – отклонение скорости частиц среды, c = = $c(\vec {r})\, = \,\sqrt {{{{\left( {\frac{{\partial p}}{{\partial \rho }}} \right)}}_{S}}} $ – скорость распространения акустической волны, определяемая параметрами среды.

В матричном виде в одномерном случае она записывается как:

(5)
${{\vec {U}}_{t}} + {\mathbf{A}}{{\vec {U}}_{x}} = \vec {0},$
где нижние индексы $x$ и $t$ обозначают дифференцирование по координате и времени, соответственно, а вектор $\vec {U}$ и матрица A имеют следующий вид:

(6)
$\vec {U} = \left( {\begin{array}{*{20}{c}} V \\ p \end{array}} \right),~\quad {\mathbf{A}} = \left( {\begin{array}{*{20}{c}} 0&{\frac{1}{\rho }} \\ {\rho {{c}^{2}}}&0 \end{array}} \right).$

Матрицу ${\mathbf{A}}$ можно диагонализовать, используя матрицу перехода R:

(7)
${\mathbf{R}} = \frac{1}{2}\left( {\begin{array}{*{20}{c}} 1&1 \\ {\rho c}&{ - \rho c} \end{array}} \right),\quad {{{\mathbf{R}}}^{{ - 1}}} = \left( {\begin{array}{*{20}{c}} 1&{\frac{1}{{\rho c}}} \\ 1&{ - \frac{1}{{\rho c}}} \end{array}} \right).$

Сделаем замену переменных (переход в инварианты Римана):

(8)
$\vec {\Omega } = \left( {\begin{array}{*{20}{c}} {{{\omega }^{ + }}} \\ {{{\omega }^{ - }}} \end{array}} \right) = {{{\mathbf{R}}}^{{ - 1}}}\vec {U} \Rightarrow \vec {U} = {\mathbf{R}}\vec {\Omega }\,.$

В общем случае матрица R зависит от координат, поэтому вносить ее напрямую под знак дифференцирования по координате нельзя, необходимо учитывать ее производную.

Система (5) примет вид:

(9)
$\begin{array}{*{20}{c}} {{{{\mathbf{R}}}^{{ - 1}}} \cdot \left| {{\mathbf{R}}\frac{{\partial{ \vec {\Omega }}}}{{\partial t}}} \right. + {\mathbf{A}}\left( {{\mathbf{R}}\frac{{\partial{ \vec {\Omega }}}}{{\partial x}} + \frac{{\partial {\mathbf{R}}}}{{\partial x}}\vec {\Omega }} \right) = 0,} \\ {\frac{{\partial{ \vec {\Omega }}}}{{\partial t}} + {{{\mathbf{R}}}^{{ - 1}}}{\mathbf{AR}}\frac{{\partial{ \vec {\Omega }}}}{{\partial x}} + \left( {{{{\mathbf{R}}}^{{ - 1}}}{\mathbf{A}}\frac{{\partial {\mathbf{R}}}}{{\partial x}}} \right)\vec {\Omega } = 0.} \end{array}$

В итоге мы приходим к следующей матричной форме записи рассматриваемой системы:

(10)
$\begin{array}{*{20}{c}} {\frac{{\partial{ \vec {\Omega }}}}{{\partial t}} + {\mathbf{\Lambda }}\frac{{\partial{ \vec {\Omega }}}}{{\partial x}} + {\mathbf{M}}\vec {\Omega } = 0,} \\ {{\mathbf{\Lambda }} = \left( {\begin{array}{*{20}{c}} c&0 \\ 0&{ - c} \end{array}} \right),\quad {\mathbf{M}} = \frac{1}{2}\left( {{{c}_{x}} + \frac{c}{\rho }{{\rho }_{x}}} \right)\left( {\begin{array}{*{20}{c}} 1&{ - 1} \\ 1&{ - 1} \end{array}} \right).} \end{array}$

В работе рассматривается случай линейных зависимостей для плотности среды и скорости распространения акустических волн от координаты, когда ${{c}_{x}} = {{\alpha }_{c}}$ и ${{\rho }_{x}} = {{\alpha }_{\rho }}$. Рассмотрим часть уравнения, которая содержит только частные производные. Мы можем найти характеристики, вдоль которых уравнение в частных производных сводится к уравнению в полных дифференциалах:

(11)
$\begin{array}{*{20}{c}} {\frac{{\partial {{\omega }^{ + }}}}{{\partial t}} + c\left( x \right)\frac{{\partial {{\omega }^{ + }}}}{{\partial x}} = \frac{{d\xi }}{{dt}},} \\ {\xi \left( t \right) = {{\omega }^{ + }}(t,{{x}^{ + }}\left( t \right)).} \end{array}$

При этом ${{x}^{ + }}\left( t \right)$ находится из дифференциального уравнения для характеристики:

(12)
$\begin{array}{*{20}{c}} {\frac{{d{{x}^{ + }}}}{{dt}} = c\left( x \right) = {{c}_{0}} + {{\alpha }_{c}}x,} \\ {{{x}^{ + }}\left( t \right) = \frac{{c\left( {{{x}_{0}}} \right){{e}^{{{{\alpha }_{c}}\left( {t - {{t}_{0}}} \right)}}} - {{c}_{0}}}}{{{{\alpha }_{c}}}}.} \end{array}$

То же самое можно выполнить и для второго инварианта:

(13)
$\begin{array}{*{20}{c}} {\frac{{\partial {{\omega }^{ - }}}}{{\partial t}} - c\left( x \right)\frac{{\partial {{\omega }^{ - }}}}{{\partial x}} = \frac{{d\zeta }}{{dt}},} \\ {\zeta \left( t \right) = {{\omega }^{ - }}(t,{{x}^{ - }}\left( t \right)),} \end{array}$
(14)
$\begin{array}{*{20}{c}} {\frac{{d{{x}^{ - }}}}{{dt}} = - c\left( x \right) = - \left( {{{c}_{0}} + {{\alpha }_{c}}x} \right),} \\ {{{x}^{ - }}\left( t \right) = \frac{{c\left( {{{x}_{0}}} \right){{e}^{{ - {{\alpha }_{c}}\left( {t - {{t}_{0}}} \right)}}} - {{c}_{0}}}}{{{{\alpha }_{c}}}}.} \end{array}$

Здесь $\left( {{{x}_{0}},{{t}_{0}}} \right)$ – точка, находящаяся на характеристике.

При описанной выше замене переменных система уравнений (5) принимает вид:

(15)
$\begin{array}{*{20}{c}} {\frac{{d\vec {\Psi }}}{{dt}} + {\mathbf{M}}(t)\vec {\Psi } = 0,} \\ \begin{gathered} {\mathbf{M}}(t) = \left( {\begin{array}{*{20}{c}} {a({{x}^{ + }}(t))}&{ - a({{x}^{ + }}(t))} \\ {a({{x}^{ - }}(t))}&{ - a({{x}^{ - }}(t))} \end{array}} \right), \hfill \\ a(x) = \frac{1}{2}\left( {{{\alpha }_{c}} + \frac{{{{c}_{0}} + {{\alpha }_{c}}x}}{{{{\rho }_{0}} + {{\alpha }_{\rho }}x}}{{\alpha }_{\rho }}} \right). \hfill \\ \end{gathered} \end{array}$

В работе для ее решения использовался модифицированный метод Эйлера с пересчетом второго порядка:

(16)
$\begin{array}{*{20}{c}} {{{{\vec {\Psi }}}^{{n + 1}}} = {{{\vec {\Psi }}}^{n}} + \frac{\tau }{2}\left( { - {\mathbf{M}}\left( {{{t}_{n}}} \right){{{\vec {\Psi }}}^{n}} - {\mathbf{M}}\left( {{{t}_{{n + 1}}}} \right){{{\vec {\Psi }}}^{{n + 1/2}}}} \right),} \\ {{{{\vec {\Psi }}}^{{n + 1/2}}} = {{{\left( {{\mathbf{E}} + \frac{\tau }{2}{\mathbf{M}}\left( {{{t}_{{n + 1}}}} \right)} \right)}}^{{ - 1}}}\left( {E - \frac{\tau }{2}{\mathbf{M}}\left( {{{t}_{n}}} \right)} \right){{{\vec {\Psi }}}^{n}},} \end{array}$
а также явный метод Рунге–Кутты третьего порядка:
${{\vec {\Psi }}^{{n + 1}}} = {{\vec {\Psi }}^{n}} + \frac{1}{6}({{{{\vec {k}}}}_{1}} + 4{{{{\vec {k}}}}_{2}} + {{{{\vec {k}}}}_{3}}),$
(17)
$\begin{gathered} {{{{{\vec {k}}}}}_{1}} = - \tau {\mathbf{M}}\left( {{{t}_{n}}} \right){{{\vec {\Psi }}}^{n}}, \\ {{{{{\vec {k}}}}}_{2}} = - \tau {\mathbf{M}}\left( {{{t}_{n}} + \frac{\tau }{2}} \right)\left( {{{{\vec {\Psi }}}^{n}} + \frac{{{{{{{\vec {k}}}}}_{1}}}}{2}} \right), \\ \end{gathered} $
${{{{\vec {k}}}}_{3}} = - \tau {\mathbf{M}}\left( {{{t}_{n}} + \tau } \right)({{\vec {\Psi }}^{n}} + 2{{{{\vec {k}}}}_{2}} - {{{{\vec {k}}}}_{1}}),$
где

(18)
${{\vec {\Psi }}^{n}} = \left( {\begin{array}{*{20}{c}} {\xi \left( {{{t}_{n}}} \right)} \\ {\zeta \left( {{{t}_{n}}} \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{\omega }^{ + }}({{t}_{n}},{{x}^{ + }}\left( {{{t}_{n}}} \right))} \\ {{{\omega }^{ - }}({{t}_{n}},{{x}^{ - }}\left( {{{t}_{n}}} \right))} \end{array}} \right).$

В общем случае характеристики не проходят через узлы расчетной сетки, поэтому чтобы найти значения искомых функций $\xi $ и $\zeta $ в точке пересечения характеристической кривой с предыдущим слоем по времени, использовалась интерполяция полиномом второй/третьей степени на фиксированном шаблоне.

Таким образом, полный расчетный алгоритм заключается в следующем:

1. Из каждой точки пространственной расчетной сетки на следующем временном слое выпускаем характеристики обратно до пересечения с предыдущим временным слоем.

2. В каждой точке пространственной расчетной сетки на предыдущем временном слое переходим к характеристическим переменным со своими акустическими свойствами (плотностью и скоростью звука) по формуле (8).

3. Используя полиномиальную интерполяцию второго/третьего порядка, рассчитываем значение ${{\vec {\Psi }}^{n}}$ в точке пересечения характеристической кривой с предыдущим слоем по времени.

4. По формулам (16)/(17) вычисляем ${{\vec {\Psi }}^{{n + 1}}}$ в рассматриваемой точке пространственной расчетной сетки.

5. Переходим обратно к исходным физическим переменным по формуле (8).

Для случая кусочно-постоянных коэффициентов использовался сеточно-характеристический метод, описанный в работе [17], и обладающий вторым порядком аппроксимации.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Для сравнения двух вычислительных подходов была рассмотрена следующая постановка задачи. Дана одномерная градиентная акустическая среда, в которой заданы гладкие начальные импульсы скорости и давления:

$\begin{gathered} x \in \left[ { - 1000;1000} \right], \\ t \in \left[ {0;0.25} \right], \\ \end{gathered} $
(19)
$\begin{gathered} c = 3000 + x, \\ \rho = 2500 + 0.5x, \\ {v}\left( {0,x} \right) = \left\{ {\begin{array}{*{20}{l}} {{\text{si}}{{{\text{n}}}^{4}}\left( {x\frac{\pi }{{50}}} \right),~\quad x \in \left[ {0;50} \right],} \\ {0,~\quad x \notin \left[ {0;50} \right],} \end{array}} \right. \\ \end{gathered} $
$p\left( {0,x} \right) = \rho \left( x \right)c\left( x \right){v}\left( {0,x} \right).$

Выбор функции sin4(x) обусловлен ее достаточно гладкой сшивкой с нулем на границах рассматриваемой области [0; 50]. Была проведена серия численных расчетов, отличающихся применяемым численным методом. Использовались согласованные по порядку аппроксимации процедуры полиномиальной интерполяции и интегрирования системы вдоль характеристической кривой. Исследовался вопрос уменьшения ошибки численного решения при измельчении расчетной сетки в диапазоне от 2000 до 256 000 расчетных ячеек. При измельчении пространственной сетки уменьшался и шаг по времени так, чтобы обеспечить постоянство числа Куранта. На рис. 1 и 2 представлены графики решений, полученные тремя рассматриваемыми методами для сетки наибольшей мелкости. Они свидетельствуют о минимальном различии в полученных численных решениях, что подтверждает возможность использования любого из них.

Рис. 1.

Профили давления (слева) и скорости (справа), рассчитанные с использованием предложенной в работе модификации сеточно-характеристического метода второго (1) и третьего (2) порядка, а также методом из работы [17] (3).

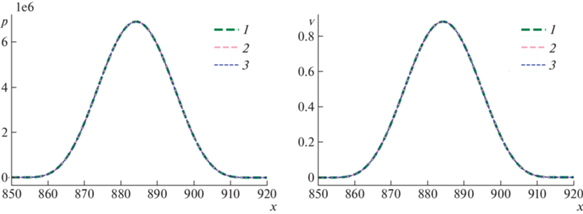
Рис. 2.

Разность профилей давления (слева) и скорости (справа), рассчитанная между результатами, полученными методом из работы [17] и с использованием предложенной в работе модификации сеточно-характеристического метода второго (1) и третьего (2) порядка.

В работе также было исследовано поведение ошибки численного решения при измельчении расчетной сетки от 2000 до 256 000 ячеек. Графики зависимости логарифма ошибки (относительно численного решения на самой мелкой сетке) от логарифма числа ячеек для каждого из методов представлены на рис. 3.

Рис. 3.

График зависимости логарифма ошибки от логарифма числа ячеек в сетке при использовании предложенной в работе модификации сеточно-характеристического метода второго (1) и третьего (2) порядка, а также метода из работы [17] (3).

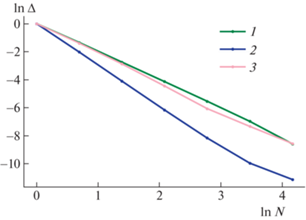
Из графиков видно, что при использовании интерполяции полиномами третьей степени и метода Рунге–Кутты третьего порядка возможно обеспечить убывание численной ошибки метода быстрее, чем для предложенного ранее метода кусочно-постоянной аппроксимации модели [17].

4. ЗАКЛЮЧЕНИЕ

В настоящей работе был исследован процесс распространения акустических волн в средах с пространственно изменяющимися параметрами: скоростью звука и плотностью. Для численного решения определяющей системы уравнений был предложен сеточно-характеристический метод, явно учитывающий наличие градиента механических параметров на масштабе расчетной ячейки. Было выполнено сравнение расчетных полей давления и скорости с результатами, полученными в рамках аппроксимации среды моделью с кусочно-постоянными параметрами. Продемонстрирована возможность построения численных методов повышенного порядка. Направлением дальнейших исследований может быть обобщение разработанного подхода на трехмерный случай. Необходимо отметить, что используемый в работе сеточно-характеристический подход позволяет построить вычислительный алгоритм для решения системы уравнений линейной теории упругости с постоянными и кусочно-постоянными коэффициентами. Однако возможность обобщения предложенного алгоритма на упругие среды с градиентным изменением параметров является предметом отдельного исследования. В таком случае область практического применения была бы расширена с задач сейсмической разведки, например, на задачи неразрушающего контроля гетерогенных материалов.

Список литературы

  1. Young C., Shragge J., Schultz W., Haines S., Oren C., Simmons J., Collett T.S. Advanced distributed acoustic sensing vertical seismic profile imaging of an Alaska North Slope gas hydrate field. Energy & Fuels. 2022. V. 36. № 7. P. 3481–3495.

  2. Chai X., Tang G., Wang F., Gu H., Wang X. Q-compensated acoustic impedance inversion of attenuated seismic data: Numerical and field-data experiments. Geophysics. 2018. V. 83. № 6. P. R553–R567.

  3. Wang E., Ba J., Liu Y. Time-space-domain implicit finite-difference methods for modeling acoustic wave equations. Time-space-domain implicit FD. Geophysics. 2018. V. 83. № 4. P. T175–T193.

  4. Amini N., Shin C., Lee J. Second-order implicit finite-difference schemes for the acoustic wave equation in the time-space domain. Geophysics. 2021. V. 86. № 5. P. T421–T437.

  5. Denner F., Evrard F., van Wachem B. G. Conservative finite-volume framework and pressure-based algorithm for flows of incompressible, ideal-gas and real-gas fluids at all speeds. Journal of Computational Physics. 2020. V. 409. art. no. 109348.

  6. Diwan G.C., Mohamed M.S. Pollution studies for high order isogeometric analysis and finite element for acoustic problems. Computer Methods in Applied Mechanics and Engineering. 2019. V. 350. P. 701–718.

  7. Adjerid S., Moon K. An immersed discontinuous Galerkin method for acoustic wave propagation in inhomogeneous media. SIAM Journal on Scientific Computing. 2019. V. 41. № 1. P. A139–A162.

  8. Фаворская А.В., Петров И.Б. О численном моделировании пространственных динамических волновых эффектов в скальных массивах. Доклады Академии наук. 2017. Т. 474. № 4. С. 418–422. https://doi.org/10.7868/S0869565217040041

  9. Петров И.Б., Голубев В.И., Петрухин В.Ю., Никитин И.С. Моделирование сейсмических волн в анизотропных средах. Доклады Российской академии наук. Математика, информатика, процессы управления. 2021. Т. 498. № 1. С. 59–64. https://doi.org/10.31857/S2686954321030140

  10. Nikitin I.S., Golubev V.I. Higher Order Schemes for Problems of Dynamics of Layered Media with Nonlinear Contact Conditions. Smart Innovation, Systems and Technologies. 2022. V. 274. P. 273–287.

  11. Golubev V., Shevchenko A., Khokhlov N., Petrov I., Malovichko M. Compact grid-characteristic scheme for the acoustic system with the piece-wise constant coefficients. 2022. International Journal of Applied Mechanics. V. 14. № 2, art. no. 2250002. https://doi.org/10.1142/S1758825122500028

  12. Golubev V.I., Shevchenko A.V., Khokhlov N.I., Nikitin I.S. Numerical investigation of compact grid-characteristic schemes for acoustic problems. Journal of Physics: Conference Series. 2021. V. 1902. № 1. art. no. 012110.

  13. Kuvshinov B.N., Mulder W.A. The exact solution of the time-harmonic wave equation for a linear velocity profile. Geophysical Journal International. 2006. V. 167. № 2. P. 659–662.

  14. Pekeris C.L. Theory of propagation of sound in a half-space of variable sound velocity under conditions of formation of a shadow zone. The journal of the acoustical society of America. 1946. V. 18. № 2. P. 295–315.

  15. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. Теоретическая физика: т. VI. 3-е изд., перераб. М.: Наука. Гл. ред. физ-мат. лит., 1986. 736 с.

  16. Бреховских Л.М., Годин О.А. Акустика слоистых сред. М.: Наука. Гл. ред. физ-мат. лит., 1989. 416 с.

  17. Хохлов Н.И. Моделирование распространения динамических волновых возмущений в гетерогенных средах на высокопроизводительных вычислительных системах: дис. … д. ф.-м. наук: 05.13.18. ФГАОУ ВО “Московский физико-технический институт (национальный исследовательский университет)”, Долгопрудный, 2022. 298 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал