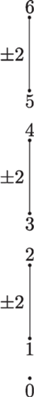Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 507, № 1, стр. 57-60

1. ЧИСЛА БРЮА В УСЛОВИЯХ АЦИКЛИЧНОСТИ

Рассмотрим гладкий кобордизм (M, ${{\partial }_{0}}M,{{\partial }_{1}}M)$, т.е. компактное многообразие M с краем ${{\partial }_{0}}M \sqcup {{\partial }_{1}}M$. Напомним, что функцией Морса на M называется функция $f:M \to [0,1]$ с лишь невырожденными критическими точками, причем такая, что ${{f}^{{ - 1}}}(0) = {{\partial }_{0}}M,$ ${{f}^{{ - 1}}}(1) = {{\partial }_{1}}M$. Если для любых двух критических точек $x$ и $y$ функции f верно, что $f(x) \ne f(y)$, то такая функция называется строгой. Мы начинаем c описания инварианта строгой функции Морса f, зависящего от поля $\mathbb{F}$ и являющегося усилением пар Баранникова [2]. Это инвариант функции (для фиксированного $\mathbb{F}$) относительно непрерывных деформаций в (несвязном) пространстве строгих функций Морса на данном многообразии. Интерес представляет уже случай замкнутого многообразия $M$.

Для $a \in [0,1]$ положим ${{M}^{a}}\{ x \in M\,{\text{|}}\,f(x) \leqslant a\} $; это подмножество называется множеством меньших значений. Предположим, что для каждой критической точки $x \in M$ выбрана образующая в группе 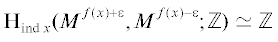, где ind x – индекс критической точки $x$, а $\varepsilon \in {{\mathbb{R}}_{ + }}$ достаточно мало. Такой выбор называется ориентацией f.

Зафиксируем строгую функцию Морса f и поле  $\mathbb{F}$. Мы переходим к описанию множества значений, принимаемых инвариантом пары $(f,\mathbb{F})$. Инвариант состоит из двух частей: пар Баранникова (для краткости, просто пар) и чисел Брюа. Пары Баранникова – это некоторые пары $(x,y)$ критических точек f соседнего индекса, подчиняющиеся условию, что если $f(x) > f(y)$, то ${\text{ind}}\,x = {\text{ind}}\,y$ + 1. Каждая критическая точка может принадлежать максимум одной паре Баранникова. Приведенные условия являются необходимыми, но не достаточными, полное определение предъявлено ниже. Таким образом, инвариант заключает в себе, в частности, разбиение всех критических точек на верхние в паре (в наших обозначениях, x), нижние в паре (в наших обозначениях, $y$) и неспаренные. Набор пар задается, в этих терминах, биекцией между верхними точками и нижними точками индекса, меньшего на 1. Далее, число Брюа – это определяемый ниже ненулевой элемент поля $\mathbb{F}$, приписанный каждой паре Баранникова и определенный с точностью до знака. Пример для $\mathbb{F} = \mathbb{Q}$ изображен на рис. 1 (он реализуется некоторой строгой функцией Морса на S⁴). Критические точки изображены точками, упорядоченными снизу вверх по возрастанию критических значений. Индекс подписан сверху или снизу, пары обозначены отрезками. Число Брюа пары написано слева от середины соответствующего отрезка (неопределенность в знаке опущена).

2. KОНСТРУКЦИЯ ИНВАРИАНТА

Выберем какую-нибудь ориентацию f. В дальнейшем все гомологии берутся с коэффициентами в $\mathbb{F}$. Пусть $x$ и $y$ – две критические точки индексов $k + 1$ и $k$ соответственно, такие что $f(x) > f(y)$. По основной теореме теории Морса, имеется гомотопическая эквивалентность ${{M}^{{f(x) + \varepsilon }}} \simeq {{M}^{{f(x) - \varepsilon }}}{{ \cup }_{\varphi }}{{e}^{{k + 1}}}$, где ${{e}^{{k + 1}}}$ – клетка размерности k + 1, а $\varphi :{{S}^{k}} \to {{M}^{{f(x) - \varepsilon }}}$ – характеристическое отображение ее границы, которое можно считать вложением. Рассмотрим фундаментальный класс соответствующей сферы как элемент в ${{{\text{H}}}_{k}}({{M}^{{f(x) - \varepsilon }}})$. Пусть $X$ – образ этого класса при отображении ${{{\text{H}}}_{k}}({{M}^{{f(x) - \varepsilon }}}) \to {{{\text{H}}}_{k}}({{M}^{{f(x) - \varepsilon }}},{{M}^{{f(y) - \varepsilon }}})$. Далее, рассмотрим критическую точку $y$ и ее относительный фундаментальный класс как элемент в ${{{\text{H}}}_{k}}({{M}^{{f(y) + \varepsilon }}},{{M}^{{f(y) - \varepsilon }}})$. Пусть $Y$ – образ этого класса при отображении ${{{\text{H}}}_{k}}({{M}^{{f(y) + \varepsilon }}},{{M}^{{f(y) - \varepsilon }}})$ $ \to $ $ \to $ ${{{\text{H}}}_{k}}({{M}^{{f(x) - \varepsilon }}},{{M}^{{f(y) - \varepsilon }}})$, индуцированном вложением. Говорят, что точки $x$ и $y$ образуют пару Баранникова, если $X = \lambda Y \ne 0$, для некоторого $\lambda \in \mathbb{F}{\kern 1pt} * = \mathbb{F}{{\backslash }}\{ 0\} $. Число $\lambda $ называется числом Брюа соответствующей пары. При cмене ориентации функции  f некоторые числа Брюа могут лишь поменять знак.

Можно показать, что это определение пар Баранникова совпадает с введенным в [2]. Отметим, что близкие идеи о числах Брюа над $\mathbb{Q}$ возникли независимо от настоящей работы в [3].

Легко видеть, что количество неспаренных точек индекса $k$ равно $\dim {{{\text{H}}}_{k}}(M,{{\partial }_{0}}M)$. Если $\dim M \geqslant 4$ и $\mathbb{F}$ есть $\mathbb{Q}$ или ${{\mathbb{F}}_{p}}$, то по любому наперед заданному числу $\lambda \in \mathbb{F}{\kern 1pt} *$ можно построить строгую функцию Морса на $M$, имеющую $ \pm \lambda $ в качестве одного из своих чисел Брюа. Далее, рассмотрим произведение

где $\Theta $ – множество пар Баранникова функции f над $\mathbb{F}$, ${{\lambda }_{\theta }}$ – число Брюа пары $\theta $, $\deg \theta $ – индекс верхней критической точки в паре $\theta $. Мы называем это произведение альтернированным произведением чисел Брюа, по аналогии c эйлеровой характеристикой, которая является альтернированной суммой, например, чисел Бетти.

Теорема 1. Пусть f – строгая функция Морса на $M$, a  $\mathbb{F}$ – поле. Предположим, что ${{{\text{H}}}_{k}}(M,{{\partial }_{0}}M;\mathbb{F})$ = 0 для всех $0 < k < \dim M$. Тогда альтернированное произведение чисел Брюа не зависит от f (с точностью до знака).

Рассмотрим в качестве примера $M = \mathbb{R}{{\mathbb{P}}^{n}}$ (здесь ${{\partial }_{0}}M = {{\partial }_{1}}M = \emptyset $) и $\mathbb{F} = \mathbb{Q}$. Тогда это произведение равно $ \pm {{2}^{{[n/2]}}}$, где квадратные скобки обозначают целую часть. Чтобы в этом убедиться, достаточно рассмотреть стандартную функцию Морса c $n + 1$ критической точкой, инвариант которой изображен на рис. 2 (n = 6). Условие ацикличности из Теоремы 1 является существенным – для любого наперед заданного целого числа $\mu $ можно найти строгую функцию Морса f на $\mathbb{C}{{\mathbb{P}}^{2}}$, для которой альтернированное произведение чисел Брюа над $\mathbb{Q}$ равно $ \pm \mu $.

3. ОДНОПАРАМЕТРИЧЕСКАЯ ТЕОРИЯ МОРСА

Будем говорить, что две пары Баранникова $({{x}_{1}},{{y}_{1}})$ и $({{x}_{2}},{{y}_{2}})$ идут внахлест, если либо $f({{y}_{1}}) < f({{y}_{2}}) < f({{x}_{1}}) < f({{x}_{2}})$, либо f(y₂) < f(y₁) < < $f({{x}_{2}}) < f({{x}_{1}})$. Обозначим через ${\text{O}}$ количество (неупорядоченных) пар Баранникова, идущих внахлест. Для примера на рис. 1 это число равно 1. В дальнейшем нам понадобится число

не имеющее какой-либо неопределенности в знаке, но зависящее от ориентации f.

Рассмотрим типичный путь $\{ {{f}_{t}}\} $ в пространстве функций на $M$, $t \in [ - 1,1]$; eго принято называть типичным однопараметрическим семейством функций. Типичная точка семейства есть строгая функция Морса ${{f}_{{{{t}_{0}}}}}:M \to [0,1]$. С типичным семейством $\{ {{f}_{t}}\} $ связана его диаграмма Серфа [4], определяемая как подмножество точек плоскости вида $(t,a)$, где a является критическим значением функции f_t. Это подмножество есть конечное объединение образов отрезка, гладких вне своих концов; эти образы называются дугами. Дуги пересекаются лишь просто и трансверсально и не имеют вертикальных касательных. Их граничные точки есть либо каспы (т.е. негладкие точки полукубической параболы), либо точки на вертикальных прямых $t = \pm 1$.

Имеется лишь конечное число значений параметра t, в которых функция f_t не является строгой функцией Морса. Говорят, что в этих точках происходит перестройка строгой функции Морса. Такие перестройки бывают двух типов.

1. Функция ${{f}_{{{{t}_{0}}}}}$ строгая, но не морсовская. В этот момент происходит рождение или смерть двух критических точек соседнего индекса. В подходящих координатах эта ситуация моделируется семейством ${{f}_{t}}({{x}_{1}}, \ldots ,{{x}_{{\dim M}}}) = x_{1}^{3} \pm t{{x}_{1}} + Q({{x}_{2}}$, ..., x_dim M), где Q – невырожденная квадратичная форма. На диаграмме Серфа эта перестройка отвечает каспу. Можно показать, что две упомянутые точки соседнего индекса образуют пару Баранникова с числом Брюа ±1 (для любого $\mathbb{F}$, причем знак не зависит от $\mathbb{F}$).

2. Функция ${{f}_{{{{t}_{0}}}}}$ морсовская, но не строгая. В этот момент происходит обмен местами двух критических значений. На диаграмме Серфа это отвечает трансверсальному пересечению двух дуг.

Каждая дуга соответствует некоторой критической точке функции f_t для $t \in (a,b) \subset [ - 1,1]$, где $(a,b)$ – проекция внутренних точек этой дуги в $[ - 1,1]$. Пусть количество дуг равно $N$. Тогда, сделав ${{2}^{N}}$ бинарных выборов, мы можем согласованно ориентировать все строгие функции Морса семейства $\{ {{f}_{t}}\} $. Обозначим через ${\text{C}}$ количество каспов с числом Брюа –1, а через ${\text{X}}$ – число самопересечений диаграммы Серфа (т.е. перестроек второго типа). Очевидно, ${\text{X}}$ – инвариант семейства, т.е. число, не зависящее от ориентаций.

Пусть $\mathbb{F}$ – поле характеристики не два. Предположим, что ${\text{H}}_{*}^{{}}(M,{{\partial }_{0}}M;\mathbb{F}) = 0$. В таком случае, согласно предыдущей части этой заметки, у любой строгой функции Морса f_t нет неспаренных точек и $\tau ({{f}_{t}},\mathbb{F})$ не зависит от f_t с точностью до знака. Нетрудно показать, что знак $\frac{{\tau ({{f}_{1}},\mathbb{F})}}{{\tau ({{f}_{{ - 1}}},\mathbb{F})}}{{( - 1)}^{{\text{C}}}} \in \{ \pm 1\} $ является инвариантом семейства. Следующая теорема устанавливает связь между двумя введенными инвариантами.

Теорема 2. Пусть $\mathbb{F}$ – поле характеристики не два, a $(M,{{\partial }_{0}}M,{{\partial }_{1}}M)$ – такой кобордизм, что ${{{\text{H}}}_{*}}(M,{{\partial }_{0}}M;\mathbb{F}) = 0$. Пусть также $\{ {{f}_{t}}\} $ – типичное однопараметрическое семейство функций на $M$ (как-либо ориентированное). Тогда справедливо равенство

Это равенство по модулю два, записанное в мультипликативной нотации.

4. О ДОКАЗАТЕЛЬСТВАХ И СВЯЗЯХ С ИЗВЕСТНЫМИ РЕЗУЛЬТАТАМИ

Подробности и доказательства обеих теорем описываются в работе [5]. Для доказательств вводится модификация понятия полного флага на цепном комплексе над полем. Линейно-алгебраическое ядро доказательств – разложение Брюа для $G{{L}_{n}}(\mathbb{F})$. Необходимость последовательного изложения этих инструментов делает геометрические результаты менее доступными. С другой стороны, если ограничиться формулировками, то оказывается, что можно обойтись лишь языком элементарной дифференциальной топологии, что и сделано в настоящей заметке.

Теорема 2 доказана в [1] в следующих дополнительных предположениях.

1) Функции ${{f}_{{ - 1}}}$ и ${{f}_{1}}$ не имеют критических точек (как следствие, кобордизм тривиален, т.е. $M = {{\partial }_{0}}M \times [0,1]$). В нашем контексте это означает, что первый из трех множителей в вышеприведенной формуле равен 1.

2) Многообразие ${{\partial }_{0}}M$ либо односвязно и стабильно параллелизуемо, либо имеет размерность не меньше 5.