Доклады Российской академии наук. Математика, информатика, процессы управления, 2023, T. 510, № 1, стр. 33-38

1. ВВЕДЕНИЕ

В ${{Q}_{T}} = [0,T] \times \Omega $, где $\Omega \in {{R}^{N}}$, N = 2, 3 – ограниченная область с гладкой многосвязной границей $\partial \Omega $ рассматривается движение вязкоупругой жидкости типа Олдройда (см. [1]), описываемое начально-краевой задачей

Относительно области Ω предполагается, что она получается удалением из ограниченной области ${{\Omega }_{0}}$ попарно непересекающихся множеств ${{\overline \Omega }_{i}}$, $i = 1,...,K$, где области ${{\Omega }_{i}} \subset {{\Omega }_{0}}$. Таким образом, $\Omega = {{\Omega }_{0}}{{\backslash }}( \cup _{{i = 1}}^{K}{{\overline \Omega }_{i}})$. При этом граница $\partial \Omega = \cup _{{i = 0}}^{K}{{\Gamma }_{i}}$ области Ω такова, что поверхность ${{\Gamma }_{0}} = \partial {{\Omega }_{0}}$ ограничивает область $\Omega $ извне, а остальные связные компоненты ${{\Gamma }_{i}}$, $i = 1,...,K$, ее границы (${{\Gamma }_{i}} = \partial {{\Omega }_{i}}$) заключены внутри этой поверхности.

В (1)–(4) $u(t,x)$ = $({{u}_{1}}(t,x), \ldots ,{{u}_{N}}(t,x))$ и $p(t,x)$ – искомые векторная и скалярная функции, означающие скорость движения и давление среды, $f(t,x)$ – плотность внешних сил, $\mathcal{E}(u)$ = $\{ {{\mathcal{E}}_{{ij}}}(u)\} _{{i,j = 1}}^{N}$ – тензор скоростей деформаций, т.е. матрица с коэффициентами ${{\mathcal{E}}_{{ij}}}(u) = \frac{1}{2}(\partial {{u}_{i}}{\text{/}}\partial {{x}_{j}} + \partial {{u}_{j}}{\text{/}}\partial {{x}_{i}})$. Дивергенция ${\text{Div}}{\kern 1pt} \mathcal{E}(u)$ матрицы определяется как вектор с компонентами – дивергенциями строк, ${{\mu }_{0}} > 0$, $\lambda > 0$, ${{\mu }_{1}} \geqslant 0$ – константы, характеризующие вязкоупругие свойства жидкости, u⁰ и $\alpha $ – заданные начальное и граничное значения функции u. Вектор-функция $z(\tau ;t,x)$ определяется как решение задачи Коши (4).

В условиях однозначной разрешимости задачи Коши (4) функция ${{\tau }_{u}}(t,x)$ определяется как ${{\tau }_{u}}(t,x) = \inf \{ \tau :z(s;t,x) \in \Omega {\kern 1pt} \;{\text{при}}\;s \in [\tau ,t]\} $. Множество γ(t, x) = $\{ y:y = z(s;t,x),\;{{\tau }_{u}}(t,x) \leqslant s \leqslant t\} $ определяет траекторию движения по $\Omega $ частицы жидкости, которая в момент времени t находится в точке $x \in \Omega $. Если ${{\tau }_{u}}(t,x) = 0$, то движение данной частицы по траектории $\gamma (t,x)$ начинается с нулевого момента времени. Если ${{\tau }_{u}}(t,x) > 0$, то в этот момент времени частица занимает положение $z({{\tau }_{u}}(t,x);t,x) \in \partial \Omega $, и ${{\tau }_{u}}(t,x)$ означает момент вхождения данной частицы в $\Omega $ через $\partial \Omega $ извне. Заметим, что наличие интеграла в (1) означает (см. [2, гл. 7]) наличие памяти среды вдоль траекторий поля скоростей.

В случае односвязной границы $\partial \Omega $ и однородного граничного условия ($\alpha = 0$, ${{\tau }_{u}}(t,x) = 0$) в (1), нелокальные теоремы существования и единственности слабых и сильных решений для систем вида (1)–(4) устанавливались в [3–6].

Уже для систем уравнений Навье–Стокса (${{\mu }_{1}} = 0$) случай многосвязной границы $\partial \Omega $ является существенно более сложным по сравнению со случаем односвязной границы и достаточно полно исследован с точки зрения разрешимости для стационарной задачи в плоском случае.

Вследствие условия ${\text{div}}{\kern 1pt} u = 0$ функция α должна удовлетворять соотношению

Здесь $n(x) = ({{n}_{1}}(x), \cdots ,{{n}_{N}}(x))$ – вектор внешней нормали к $\partial \Omega $ в точке $x \in \partial \Omega $, ${{F}_{i}} = \int\limits_{{{\Gamma }_{i}}}^{} {\alpha (x) \cdot n(x){\kern 1pt} dx} $, $i = 0,1, \ldots ,K$. Принципиальные трудности возникают в случае, когда не все потоки ${{F}_{i}}$ равны нулю (т.е. задачи протекания) (см., напр., [7–12] и имеющуюся там библиографию).

Нелокальная слабая разрешимость задаче протекания для системы уравнений Навье–Стокса (как 2-D, так 3-D) в случае многосвязной границы установлена при различных условиях на граничную функцию (см., напр., [7, 10, 11] и имеющуюся там библиографию).

В настоящей работе мы устанавливаем слабую разрешимость задачи (1)–(4) в классе функций $u \in {{L}_{2}}(0,T;W_{2}^{1}{{(\Omega )}^{N}})$ в случае многосвязной границы $\partial \Omega $ при ${{\mu }_{1}} \ne 0$ и неравенства нулю потоков ${{F}_{i}}$ (т.е. задачи протекания). При этом вопрос об однозначной разрешимости задачи Коши (4) становится нетривиальным и понимается в смысле теории регулярных лагранжевых потоков (РЛП). Чтобы избежать неоправданных сложностей в доказательствах, мы считаем границу области и граничную функцию достаточно гладкими, хотя основные результаты справедливы и при более слабых ограничениях.

2. ВСПОМОГАТЕЛЬНЫЕ РЕЗУЛЬТАТЫ

3. ОСНОВНОЙ РЕЗУЛЬТАТ

Для формулировки основного результата нам будет удобно, полагая $u = v + a$, переписать задачу (1)–(4) в виде

Здесь τ(t, x) = $\inf \{ \tau \,:\,\mathcal{Z}(v)(s;t,x)\, \in \,\Omega \;{\text{при}}\;s\, \in \,[\tau ,t]\} $, ${{v}^{0}} = {{u}^{0}} - a$.

Введем пространство W₁ = $\{ v\,:\,v\, \in \,{{L}_{2}}(0,T;V)$, $v{\kern 1pt} '\, \in \,{{L}_{1}}(0,T;{{V}^{{ - 1}}})$. Здесь $v{\kern 1pt} '$ означает производную по t функции $v(t, \cdot )$ как функции со значениями в ${{V}^{{ - 1}}}$. Пусть $b(u,v,w) = \sum\limits_{i,j = 1}^N {\int\limits_\Omega ^{} {{{u}_{i}}{{v}_{j}}\partial {{w}_{j}}{\text{/}}\partial {{x}_{i}}{\kern 1pt} dx} } $, $u,{v},w \in V$.

Определение 1. Пусть $f \in {{L}_{2}}(0,T;{{V}^{{ - 1}}})$, ${{v}^{0}} \in H$. Слабым решением задачи (7)–(9) называется функция $v \in {{W}_{1}}$, удовлетворяющая условиям (9) и тождеству

Замечание. Так как слабое решение $v(t,x)$ задачи (7)–(9) принадлежит пространству ${{W}_{1}}$, то (см. [13], лемма III.1.4), $v(t,x)$ слабо непрерывна по t как функция со значениями в H, поэтому начальное условие (9) имеет смысл.

Сформулируем основной результат.

Теорема 1. Пусть $f \in {{L}_{2}}(0,T;{{V}^{{ - 1}}})$, ${{v}^{0}} \in H$. Пусть для α выполняются условия раздела 2.2. Тогда существует слабое решение задачи (7)–(9).

4. СХЕМА ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ 1

Ниже для простоты изложения опускаем непринципиальный множитель $\exp ((s - t){\text{/}}\lambda )$ в (10). Обозначим через A действующий в H оператор с областью определения 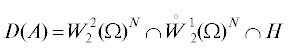, определенный дифференциальным выражением $Av = - \mathcal{P}{\text{Div}}{\kern 1pt} \mathcal{E}({v})$, где $\mathcal{P}$ – ортопроектор ${{L}_{2}}{{(\Omega )}^{N}}$ на H. Оператор A является положительно определенным самосопряженным оператором (см. [13, c. 40], [16, 2.4]). Ортонормированная система собственных векторов ${{e}_{1}},{{e}_{2}}, \ldots $ с собственными значениями $0 < {{\lambda }_{1}},{{\lambda }_{2}}, \ldots $ образует базис в H.

Зафиксируем натуральное число n. Обозначим через ${{\mathcal{P}}_{n}}$ оператор ортогонального проектирования в H на подпространство ${{H}_{n}}$, порожденное элементами ${{e}_{1}},{{e}_{2}}, \ldots ,{{e}_{n}}$. В силу плотности множества гладких функций в ${{L}_{2}}(0,T;{{V}^{{ - 1}}})$, аппроксимируем f последовательностью гладких функций ${{f}^{n}}(t,x)$, так что ${\text{li}}{{{\text{m}}}_{{n \to + \infty }}}{\text{||}}f - {{f}^{n}}{\text{|}}{{{\text{|}}}_{{{{L}_{2}}(0;W_{2}^{{ - 1}}{{{(\Omega )}}^{N}})}}} = 0$.

Будем искать галеркинские приближения ${{v}^{n}}$ в виде ${{v}^{n}}(t,x) = \sum\limits_{k = 1}^n {{{g}_{k}}(t){{e}_{k}}(x)} $ как решение тождества

Здесь ${{\tau }^{n}}(t,x) = \inf \{ \tau :{{z}^{n}}(s;t,x) \in \Omega ,s \in [\tau ,t]\} $, а ${{z}^{n}}$ – решение задачи Коши

При этом мы считаем, что функции ${{e}_{k}}(x)$ продолжены нулем из $\Omega $ в ${{\Omega }_{0}}$, так что и функции ${{v}^{n}}(t,x)$ считаем равными нулю при $x \in {{\Omega }_{0}}{{\backslash }}\Omega $.

Сведем задачу нахождения функции ${{{v}}^{n}}$ к задаче нахождения функций g_i.

Полагая в (11) $\varphi = {{e}_{i}}$, получим соответствующую интегро-дифференциальную систему для определения функций g и ${{z}^{n}}$:

Здесь $f_{i}^{n}(t) = ({{f}^{n}},{{e}_{i}})$, $\sum\nolimits_{k,r = 1}^n {{d}_{{kri}}}{{g}_{k}}(t){{g}_{r}}(t) \equiv {{D}_{i}}(g)$, ${{d}_{{kri}}}\, = \, - {\kern 1pt} \sum\nolimits_{j = 1}^N ({{e}_{{kj}}}{{e}_{r}},\partial {{e}_{i}}{\text{/}}\partial {{x}_{j}})$, ${{d}_{{ki}}}$ и k_i – некоторые числа. 

Решение системы (13)–(14) определяется как пара функций $g(t) = ({{g}_{1}}(t),{{g}_{2}}(t), \ldots ,{{g}_{n}}(t)) \in C{{[0,T]}^{n}}$ и ${{z}^{n}}(\tau ;t,x) \in C{{([0,T] \times [0,T] \times {{\Omega }_{0}})}^{N}}$, удовлетворяющих (13)–(14).

Лемма 1. Система (13)–(14) имеет решение.

Приведем схему доказательства Леммы 1. Пусть $g(t) = ({{g}_{1}}(t),{{g}_{2}}(t), \ldots ,{{g}_{n}}(t)$. Введем оператор Z, ставящий в соответствие функции $g(t)$ определенную на ${{G}_{0}}\, = \,[0,T]\, \times \,[0,T]\, \times \,{{\Omega }_{0}}$ функцию $z(\tau ;t,x)$ – решение задачи Коши (14) при ${{v}^{n}}(t,x)$ = = $\sum\nolimits_{k = 1}^n {{g}_{k}}(t){{e}_{k}}(x)$, так что $Z(g)$ = z. Пусть S(R) = = $\{ g:{\text{||}}g{\text{|}}{{{\text{|}}}_{{C{{{(0,T)}}^{n}}}}} \leqslant R\} $, где R > 0, – произвольный шар в $C{{(0,T)}^{n}}$. Оператор $Z:S(R) \to C{{({{G}_{0}})}^{N}}$ оказывается равномерно непрерывным на S(R), а Z : S(R) → → ${{C}^{1}}{{([0,T]\, \times \,[0,T]\, \times \,{{\Omega }_{0}})}^{N}}$, Z : S(R) → C¹([0, T] × × $[0,T]\, \times \,({{\Omega }_{0}}{{\backslash }}\Omega {{))}^{N}}$ ограниченными.

Пусть $z(\tau ;t,x)$, $(t,x) \in {{Q}_{T}}$, является решением задачи Коши (14), а τ(t, x) = inf{s : : z$(s;t,x)) \in \Omega ,s \leqslant t\} $. Введем оператор $\mathcal{T}$, ставящий в соответствие функции g(t), определяющей функцию $z(\tau ;t,x)$, функцию $\tau (t,x)$, так что $\mathcal{T}(g)\, = \,\tau (t,x)$. Оператор $\mathcal{T}:C{{[0,T]}^{n}} \to C({{Q}_{0}})$ оказывается непрерывным.

Пусть в системе (13)–(14) функция $w = ({{w}_{1}}, \cdots ,{{w}_{n}})$ считается заданной. Тогда, как и в [13], раздел III.3.2, показывается, что эта система ОДУ однозначно разрешима и справедлива оценка ${\text{||}}g{\text{|}}{{{\text{|}}}_{{C{{{(0,T)}}^{n}}}}} \leqslant M({\text{||}}w{\text{|}}{{{\text{|}}}_{{C{{{(0,T)}}^{n}}}}}\; + \;{\text{||}}{{v}^{0}}{\text{|}}{{{\text{|}}}_{H}})$.

Введем оператор G, ставящий в соответствие функции w решение g системы уравнений (13), так что $G(w) = g$. Оператор $G:C{{[0,T]}^{n}} \to C{{[0,T]}^{n}}$ является непрерывным на произвольном шаре ${{S}_{w}}(R) = \{ w:{\text{||}}w{\text{|}}{{{\text{|}}}_{{C{{{(0,T)}}^{n}}}}} \leqslant R\} $, причем множество B(R) = $\{ g\,:\,g\, = \,G(w),w\, \in \,{{S}_{w}}(R)\} $ компактно в $C{{(0,T)}^{n}}$.

Поставим в соответствие произвольной функции $w \in C{{[0,T]}^{n}}$ функцию $g = G(w)$, затем поставим в соответствие g функцию z = Z(g) = $Z(G(w))$, затем поставим в соответствие $z$ функцию $\tau \, = \,\mathcal{T}(z)\, = \,\mathcal{T}(Z(G(w)))$. Обозначим Ξ(w) = $Z(G(w))$ и $\Upsilon (w)\, = \,\mathcal{T}(Z(G(w)))$. Тогда из (13) подстановкой в левую часть первого уравнения $g\, = \,G(w)$, zⁿ = $\Xi (w)$, ${{\tau }^{n}}\, = \,\Upsilon (w)$ получаем операторное уравнение w = = K(w). С помощью принципа Шаудера доказывается

Лемма 2. Существует неподвижная точка w оператора $\mathcal{K}$.

Пусть w – неподвижная точка оператора $\mathcal{K}$. Положим $g = G(w)$, ${{z}^{n}} = \Xi (w)$, ${{\tau }^{n}}\, = \,\mathcal{T}(z)\, = \,\mathcal{T}(Z(G(w)))$. Тогда пара $g = G(w)$ и ${{z}^{n}} = \Xi (w)$ является решением системы (13)–(14).

Лемма 1 доказана.

Из Леммы 1 следует

Лемма 3. Пусть пара $g(t) = ({{g}_{1}}(t),{{g}_{2}}(t), \ldots ,{{g}_{n}}(t))$, ${{z}^{n}}(s;t,x)$ является решением системы (13)–(14). Тогда для функции ${{{v}}^{n}}(t,x) = \sum\nolimits_{k = 1}^n {{g}_{k}}(t){{e}_{k}}(x)$ выполняется интегральное тождество (11), и справедлива равномерная по n оценка

Из оценки (15) и того, что ${v}(t,x) = 0$ при $x \in {{\Omega }_{0}}{{\backslash }}\Omega $, следует слабая в ${{L}_{2}}(0,T;\mathop W\limits^ \circ {\kern 1pt} _{2}^{1}{{({{\Omega }_{0}})}^{N}}))$ и сильная в ${{L}_{2}}(0,T;{{L}_{2}}{{({{\Omega }_{0}})}^{N}}))$ сходимость ${{v}^{n}}$ к некоторой $v \in {{L}_{2}}(0,T;\mathop W\limits^ \circ {\kern 1pt} _{2}^{1}{{({{\Omega }_{0}})}^{N}})$ ( с точностью до подпоследовательности) при $n \to + \infty $. Отсюда следует (см. [14, 15]), что последовательность ${{z}^{n}}(s;t,x)$ сходится по $(s,x)$ мере к РЛП $z(s;t,x)$, порожденному $v \in {{L}_{2}}(0,T;\mathop W\limits^ \circ {\kern 1pt} _{2}^{1}{{({{\Omega }_{0}})}^{N}})$ равномерно по t. Тогда существует подпоследовательность ${{z}^{n}}(s;t,x)$, которая при п.в $(s,x) \in {{Q}_{T}}$ сходится к $z(s;t,x)$ равномерно по t. Отсюда и из свойств α выводится, что с точностью до подпоследовательности ${{\tau }^{n}}(t,x)$ сходится к $\tau (t,x)$ при $n \to + \infty $ при п.в. $(t,x) \in {{Q}_{T}}$.

Установленные утверждения о сходимости ${{v}^{n}}$, ${{z}^{n}}$ и ${{\tau }^{n}}$ позволяют перейти к пределу в (11) и получить тождество (10) и включение $v \in {{W}_{1}}$.

Таким образом, $v$ является слабым решением задачи задачи (7)–(9). Теорема 1 доказана.