Доклады Российской академии наук. Математика, информатика, процессы управления, 2023, T. 510, № 1, стр. 39-42

Рассматривается оператор Штурма–Лиувилля в ${{L}_{2}}({{\mathbb{R}}_{ + }})$, заданный дифференциальным выражением $l(y) = - y{\kern 1pt} '{\kern 1pt} '\; + q(x)y$, $x \in {{\mathbb{R}}_{ + }}.$

Здесь и далее ${{\mathbb{R}}_{ + }} = [0, + \infty )$, q = q(x) – комплекснозначная функция, принимающая значения при всех достаточно больших $x \geqslant {{x}_{0}} \geqslant 0$ в открытом секторе

Введем максимальную область:

и форму краевых условий: пусть ${{\alpha }_{0}},{{\alpha }_{1}} \in \mathbb{C}$,

Сам оператор L_U  будем рассматривать на области D_U, состоящей из таких $y \in D$, для которых $U(y) = 0$, где он действует как ${{L}_{U}}y = l(y).$

В общем случае рассматриваемый оператор не является секториальным, а числовой образ заметает всю комплексную плоскость.

Вместе с оператором ${{L}_{U}}$ введем $L_{U}^{0}$, определяемый на области $D_{U}^{0}$, состоящей из функций $y \in {{D}_{U}}$ с компактным носителем (своем для каждой такой функции y), где $L_{U}^{0}$ действует аналогично: $L_{U}^{0}y = l(y)$.

Известно [1], что $D_{U}^{0} \subset {{D}_{U}}$ плотна в ${{L}_{2}}({{\mathbb{R}}_{ + }})$, исходный оператор ${{L}_{U}}$ замкнут, а $L_{U}^{0}$ допускает замыкание. При этом может оказаться, что его замыкание $\widetilde {L_{U}^{0}} \ne {{L}_{U}}$ [2].

Случай, когда $\widetilde {L_{U}^{0}} = {{L}_{U}}$ называется определенным и представляет отдельный интерес. С одной стороны, как это следует из работы [1], реализация определенного случая эквивалентна тому, что $L_{U}^{*}\, = \,{{\bar {L}}_{{\bar {U}}}}$, где ${{\bar {L}}_{{\bar {U}}}}$ – оператор, определяющийся сопряженными краевыми условиями $\overline U (y)\, = \,\overline {{{\alpha }_{0}}} y(0)\, + \,\overline {{{\alpha }_{1}}} y{\kern 1pt} '(0)$ и сопряженным дифференциальным выражением $\overline l (y) = - y{\kern 1pt} '{\kern 1pt} '\; + \overline {q(x)} y$ аналогично L_U. С другой стороны, реализация определенного случая позволяет записать формулу для резольвенты L_U. При вещественном q это соответствует реализации случая предельной точки Вейля [3] для однородного уравнения

Лидским [2] рассмотрены потенциалы с ${\text{Re}}q \geqslant {\text{const}}$, либо $ \pm {\text{Im}}q \geqslant {\text{const}}$, и даны достаточные условия реализации определенного случая и компактности резольвенты L_U. Если при ${\text{Re}}q\, \geqslant \,{\text{const}}$ определенный случай реализуется всегда, то при неограниченной снизу вещественной части потенциала приходится прибегать к дополнительным условиям, например, условиям типа Сирса [2, 4].

Наличие ВКБ асимптотик решений (1) несколько упрощает исследование спектральных свойств L_U.

На этом пути были получены классические результаты Наймарка [6]. Недавно с помощью метода ВКБ были получены результаты Ишкиным [7] для несекториального оператора Штурма–Лиувилля. Стоит отметить, что случай несекториального оператора мало изучен, о чем более подробно сказано в [7].

Для существования ВКБ асимптотик достаточно, чтобы $q,q{\kern 1pt} ' \in A{{C}_{{{\text{loc}}}}}({{\mathbb{R}}_{ + }})$ и

см., например, [5], что обременительно и с точки зрения гладкости потенциала, и с точки зрения оценки роста его производных. Поэтому нас заинтересовал случай менее гладких q, когда решения (1), вообще говоря, таких асимптотик не имеют.

Договоримся через C обозначать произвольные положительные константы, возможно, различные в соседних формулах.

Введем условие на потенциал q, центральное для настоящей работы. Скажем, что q удовлетворяет условию A при $x \geqslant {{x}_{0}}$, если:

• потенциал $q \in {{C}^{1}}({{\mathbb{R}}_{ + }})$;

• образ $q([{{x}_{0}}, + \infty )) \subset {{\Pi }_{\kappa }}$, $\kappa \geqslant 0$;

• при $x \geqslant {{x}_{0}}$ имеет место оценка

где $p(x) = \sqrt {q(x)} $, а ветвь корня выбрана так, чтобы ${\text{Re}}p(x) > 0$ при $x \geqslant {{x}_{0}}$.

Проясним наш интерес к (2): как легко заметить, в случаях, рассмотренных Наймарком и Ишкиным, когда ${\text{|}}q{\text{|}} \to + \infty $, $\kappa > 0$, ${\text{|}}q{\kern 1pt} '{\text{/}}{{q}^{{3/2}}}{\text{|}} \to 0$, при $x \to + \infty $, выполняется не только (2), но и даже более сильная оценка при $x \gg 1$:

Положим

В ряде наших утверждений ρ, $1{\text{/|}}q{\text{|}}$, $\rho {\text{/|}}q{\text{|}}$ участвуют в определении весовых L₂-пространств. Отметим, что (3) дает возможность получить оценки:

а в итоге: что позволяет перейти от весов $\rho $, $1{\text{/|}}q{\text{|}}$, $\rho {\text{/|}}q{\text{|}}$ к более понятным ${\text{Re}}p$, $1{\text{/|}}q{\text{|}}$, ${\text{Re}}p{\text{/|}}q{\text{|}}$.

Заметим, что дополнительное условие $\kappa > 0$ безотносительно к (2) или (3) приводит к неравенству при $x \geqslant {{x}_{0}}$:

что вместе с (3) позволяет перейти уже к весам ${\text{|}}q{{{\text{|}}}^{{1/2}}}$, $1{\text{/|}}q{\text{|}}$, $1{\text{/|}}q{{{\text{|}}}^{{1/2}}}$.

Определим множество $\mathcal{N}$ тех $\lambda \in \mathbb{C}$, при которых условие A выполнено для ${{q}_{\lambda }} = q - \lambda $ при всех $x \geqslant {{x}_{0}}(\lambda )$ (для каждого $\lambda $ возможно свое ${{x}_{0}}(\lambda )$).

Лемма 1. Пусть для q условие A выполнено при всех $x \geqslant {{x}_{0}}$. Тогда

Множество $\mathcal{N}$ открыто [и не пусто] в $\mathbb{C}$.

Условия $\mathcal{N} = \mathbb{C}$ и ${\text{|}}q(x){\text{|}} \to + \infty $ при $x \to + \infty $ эквивалентны.

В формулировках результатов штрихом обо- значаем дифференцирование по x.

Теорема 1. Пусть $\mathcal{N} \ne \emptyset $, тогда реализуется определенный случай: $\widetilde {L_{U}^{0}} = {{L}_{U}}$.

Пусть $\Omega \subset \mathcal{N}$ – область. Существует функция $\eta (x,\lambda )$ ($x \in {{\mathbb{R}}_{ + }}$, $\lambda \in \Omega $) нетривиальная при всех $\lambda \in \Omega $ со следующими свойствами:

• обе функции $\eta (x,\lambda )$ и $\eta {\kern 1pt} '(x,\lambda )$ непрерывны по совокупности аргументов $(x,\lambda ) \in {{\mathbb{R}}_{ + }} \times \Omega $;

• при каждом $x \in {{\mathbb{R}}_{ + }}$ функции $\eta (x,\lambda )$ и $\eta {\kern 1pt} '(x,\lambda )$ однозначные аналитические в Ω как функции $\lambda $;

• при любом $\lambda \in \Omega $ функция $\eta (x,\lambda ) \in {{L}_{2}}({{\mathbb{R}}_{ + }})$ как функция x, является единственным нетривиальным решением уравнения

в классе решений из ${{L}_{2}}({{\mathbb{R}}_{ + }})$ с точностью до постоянного множителя (не зависящего от x, но, возможно, зависящего от λ);

Спектр L_U в $\Omega $ дискретный (собственные пространства одномерны, корневые – конечномерны), собственные значения определяются условием $\mathcal{W}(\lambda )$ = = 0, где

а размерности корневых подпространств – кратностями нулей $\mathcal{W}(\lambda )$.

Вне точек спектра в $\Omega $ формула для резольвенты L_U имеет вид:

где $\chi (x,\lambda )\, = \,{{\alpha }_{0}}\varphi (x,\lambda )\, - \,{{\alpha }_{1}}\psi (x,\lambda )$, а $\varphi (x,\lambda )$ и $\psi (x,\lambda )$ – решения задачи Коши для уравнения (4) с начальными условиями

Функцию $\eta (x,\lambda )$ мы называем решением Вейля однородного уравнения (4).

Следствие. Пусть для q условие A выполнено при всех $x \geqslant {{x}_{0}}$, и ${\text{|}}q(x){\text{|}} \to + \infty $ при $x \to + \infty $. Тогда спектр $\sigma ({{L}_{U}})$ дискретный.

Отметим, что в условиях Следствия мы утверждаем только дискретность спектра. Более сильное условие – компактность резольвенты – дается следующей Теоремой:

Теорема 2. Пусть для q условие A выполнено при всех $x \geqslant {{x}_{0}}$, и $\rho \to + \infty $ при $x \to + \infty $. Тогда резольвента ${{R}_{\lambda }}$ оператора L_U – вполне непрерывный оператор при $\lambda \notin \sigma ({{L}_{U}})$.

Следующая Теорема может быть полезной при исследовании полноты системы СПФ оператора L_U (см., например, [8]).

Теорема 3. Пусть $q \in {{C}^{1}}({{\mathbb{R}}_{ + }})$, ${\text{|}}q(x){\text{|}} \to + \infty $ при $x \to + \infty $, пусть $\kappa > 0$ и для некоторого $0 < \delta < 1$ при всех $x \geqslant {{x}_{0}}$:

Тогда

• спектр $\sigma ({{L}_{U}})$ дискретный, а резольвента ${{R}_{\lambda }}$ оператора L_U – вполне непрерывный оператор при .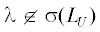

• функция $\eta (x,\lambda )$, доставляемая Теоремой 1, целая по $\lambda $ при каждом $x \geqslant 0$, и является замкнутым ядром в смысле Левина [9], т.е. если для некоторой $f \in {{L}_{2}}({{\mathbb{R}}_{ + }})$ при всех $\lambda \in \mathbb{C}$

то $f \equiv 0$.

При (2) справедливо вложение весовых пространств: ${{L}_{2}}(\rho ) \subset {{L}_{2}} \subset {{L}_{2}}(1{\text{/|}}q{\text{|}})$, в этой связи интерес представляет следующая

Теорема 4. Пусть для q условие A выполнено при всех $x \geqslant 0$, тогда ${{R}_{0}} = L_{U}^{{ - 1}}$ – ограниченный оператор из ${{L}_{2}}({{\mathbb{R}}_{ + }},1{\text{/|}}q{\text{|}})$ в ${{L}_{2}}({{\mathbb{R}}_{ + }},\rho )$, а $d{{R}_{0}}{\text{/}}dx$ (действующий как $d[({{R}_{0}}f)(x)]{\text{/}}dx$) – ограниченный оператор из ${{L}_{2}}({{\mathbb{R}}_{ + }},1{\text{/|}}q{\text{|}})$ в ${{L}_{2}}({{\mathbb{R}}_{ + }},\rho {\text{/|}}q{\text{|}})$.

Следствие. Пусть для q условие A выполнено при всех $x \geqslant 0$, тогда для любой $y \in D$ следует, что $y \in {{L}_{2}}({{\mathbb{R}}_{ + }},\rho )$, $y{\kern 1pt} ' \in {{L}_{2}}({{\mathbb{R}}_{ + }},\rho {\text{/|}}q{\text{|}})$.

БЛАГОДАРНОСТИ

Автор выражает благодарность члену-корреспонденту РАН профессору Андрею Андреевичу Шкаликову за внимание к работе и поддержку.

ИСТОЧНИК ФИНАНСИРОВАНИЯ

Работа выполнена при содействии РНФ, грант 20-11-20261.