Доклады Российской академии наук. Математика, информатика, процессы управления, 2023, T. 511, № 1, стр. 21-53

1. ВВЕДЕНИЕ

В конце XIX – первой трети XX веков были выстроены основы современного математического языка [1; 2, введение; 3, глава 4]. Во второй половине XX века этот язык – система понятий, их смыслов и применений – стал основой для построения цифровых технологий и всей цифровой цивилизации. Были предприняты попытки использовать этот язык и как основу для математического образования, и как части общечеловеческой культуры. Эти попытки дали лишь частичные результаты и встретили оппозицию с разных сторон [4].

В середине 1980-х гг. несколько представителей российской математической школы во главе с академиком Андреем Петровичем Ершовым решили начать выстраивать основы современного математического образования “с другого конца” – со стороны информатики (computer science) и старшей школы. СССР стал первой страной в мире, где такая попытка получила успешную массовую реализацию, охватившую все школы страны [5–8].

Параллельно была начата работа по построению математических оснований всей школьной математики, соответствующих задачам и возможностям современной математики и цифрового мира. Эта работа продолжается нами и сейчас, она отразилась в практике десятков школ, в издании официально признанных школьных учебников [9, 10], в Федеральных государственных образовательных стандартах [11].

В настоящей публикации представлена система математических понятий, которая последние десятилетия применяется в указанном подходе к школьной математике и информатике.

2. ГРАМОТНОСТЬ СЕГОДНЯ

Современный человек во все большей степени должен постоянно осуществлять осознанный выбор, самостоятельно добывать информацию и вести исследование обстановки. Это относится практически ко всем видам деятельности и ситуациям, начиная от домашнего хозяйства и завершая тонкими технологическими процессами. И сегодня умение ориентироваться в неожиданной ситуации, решать непредвиденные задачи оказывается намного важнее, чем “четко следовать инструкции”, “выполнять, не рассуждая и не обсуждая”. Это связано с двумя в равной степени важными и взаимосвязанными обстоятельствами:

● Уровень развития технологий сегодня позволяет поручить машине – цифровым технологиям – практически любую деятельность по заранее известным правилам и алгоритмам.

● Потребности общества, технологии, зависимость всего от решений и поведения отдельного человека, постоянная турбулентность – VUCA [12] – в большой степени влияют на поведение человека и принятие им решений.

При этом закономерными и повсеместно реализуемыми сценариями школьного образовательного процесса, да и всей жизни школы является как раз противоположное: школа все еще настроена на репродуктивные, исполнительские модели деятельности. Школа XXI века по-прежнему придерживается приоритетов XIX века.

Начальная школа веками учит ребенка “читать, писать и считать”. Все эти умения и в компьютерную эпоху считаются столпами грамотности. Однако некоторые элементы этих умений сегодня совершенно теряют смысл. В большинстве же случаев эти традиционные умения радикально трансформируются, если посмотреть на них с точки зрения современного работника и работодателя, или просто человека как развивающейся личности. Вот как выглядит сегодня результат этой трансформации:

● Читать. Большая часть письменных источников сегодня уже доступна в звуковой форме. Иногда видео-аудио инструкция является предпочтительнее письменной, как, например, кулинарный рецепт или инструкция по выполнению каких-то действий на рабочем месте. Ключевой становится функциональная коммуникативная грамотность: способность понять другого и способность применить и/или передать другому свое понимание; представление информации, в том числе – не текстовое, это вопрос прагматики.

● Писать. Письмо на клавиатуре всюду, кроме школы, вытеснило письмо ручкой на бумаге, сам процесс написания текста и создания содержания сообщения также изменился. Короткие мгновенные сообщения – устные и письменные – трансформировали коммуникативную культуру. Автоматическое преобразование устного текста в письменный используется все более широко. При этом, видимо, работа с письменным текстом, его редактирование, в течение ближайших лет будет иметь смысл.

● Считать. Потребность подсчета руками или глазами количества предметов (в старинной терминологии – “счисление”) осталась, но потребность в письменном выполнении арифметических операций (например, столбиком на бумаге) исчезла, она передана компьютеру.

3. МАТЕМАТИЧЕСКАЯ ГРАМОТНОСТЬ СЕГОДНЯ

В области математики начальная школа сегодня пытается научить всех учащихся следующему:

● Точно и быстро выполнять арифметические операции – тем самым поручить детям выполнять работу арифмометра или калькулятора.

● Распознавать в тексте задачи систему отношений между числовыми переменными. Как правило, отношения относятся к небольшому числу ситуаций, обозначаемых словесными конструкциями: “вместе”, “навстречу друг другу”, “вытекает из трубы”, “против течения”, “на равные части”, “на следующий день”. После того, как нужная система отношений выстроена – выстраивать последовательность (линейный алгоритм) вычислений нужных величин либо арифметическим способом, либо составлением системы алгебраических уравнений, решаемой по стандартному алгоритму. В XXI веке это может делать и с успехом делает искусственный интеллект.

Заметим, что в названии образовательной области начального образования слово “Арифметика” давно сменилось словом “Математика”, а в стандартах 2010 г. в нашей стране она уже закономерно стала интегрированной областью “Математика и информатика”. Но на содержании курса все эти изменения отразились несущественно.

При этом именно математика открывает практически неограниченные возможности формирования у детей способности решать задачи, которые “неизвестно-как-решать”. Важность этого умения относится не только к математике: способность решать новые, не встречавшиеся ранее человеку задачи, востребована практически во всех областях знания и технологии. Есть ли возможность изменить существующую ситуацию и начать формировать указанные способности у учащихся уже в начальной школе?

В течение трех последних десятилетий коллективом, к которому относятся авторы настоящей статьи, ведется разработка курсов “Информатика” и “Математика и информатика” для начальной школы, в которых сохранены цели традиционной арифметики, но снижен приоритет “отработки механических навыков”, в частности, для вычислений разрешено использовать калькулятор. За это время курсы использовались в образовательном процессе нескольких сотен школ. При этом соблюдались следующие принципы:

● Открытие и изобретение математики учащимися. Вместо предъявления готовых правил и алгоритмов создаются условия, где у учеников формируется и реализуется потребность самостоятельно открыть и сформулировать эти правила и алгоритмы под руководством и с помощью учителя.

● Современные базовые объекты. Класс базовых объектов, которые учащийся использует в учебной деятельности, расширен – включены основные элементарные объекты современной математики и информатики. Эти объекты, как и числа, представлены в наглядной форме, что позволяет с самого начала охватить всех учащихся независимо от уровня их начальной подготовки и поддерживать их включенность в образовательный процесс.

● Снижение приоритетности и затрат (мотивационных и временных) на отработку вычислительных навыков. Ученикам предоставляется возможность совершенствоваться в вычислениях и одновременно обеспечивается возможность использовать для вычислений технологические инструменты.

● Новизна. Указанные выше факторы открыли возможности для реализации важнейшего принципа новизны: высокой степени новизны и неожиданности для учащегося предлагаемых ему задач. Задачи при этом вполне посильны большинству учащихся для самостоятельного решения или решения с обсуждением с учителем.

● Связь с повседневной жизнью учащегося и реальным миром.

● Обратная связь. Наглядность объектов и операций над ними дает возможность ученику самостоятельно или с помощью учителя находить свои ошибки. При использовании объектов в цифровой среде возможности для обратной связи еще выше.

● Систематичность. Все упомянутые принципы реализуются в рамках системы результатов, в том числе, предусматриваемой стандартами.

Поясним более детально указанные принципы на примерах.

Открытие и изобретение математики учащимися. Важнейшие элементы арифметики могут быть самостоятельно построены учащимся на уроках математики. Скажем, десятичная система счисления может быть изобретена ребенком как способ пересчитать любое количество предметов в банке (например – спичек или фасолин), если в его распоряжении только десять цифр. Таблицы сложения и умножения могут быть построены путем подсчета клеток в полосках и прямоугольниках.

Мы поощряем самостоятельность учащихся даже в решении частных арифметических задач. Устный счет представляется не соревнованием в скорости, а развитием навыков подтверждения, обеспечения верности полученного результата. Так, результат 7 + 8 = 15 можно проверить разными способами: сложить две семерки и дополнить одну из них до 8, разложить каждое слагаемое в сумму 5 и какого-то еще числа, дополнить одно из слагаемых до 10 и т.п. Проверка, подтверждение результата вычисления путем подсчета другими способами также является примером жизненной стратегии. Мы, с одной стороны, учим детей абсолютности истины в математике, но, с другой стороны, обращаем их внимание на то, что человек может ошибиться, предполагая, что он эту истину открыл. Учитель раз за разом спрашивает детей “Как ты считал(а)?” и помогает детям формулировать изобретенные ими приемы вычисления на грамотном математическом языке, понятном его одноклассникам. Прием может даже получить имя своего создателя: “Ванин способ сложения” – это особенно важно, если изобретший его ребенок не является самым сильным математиком в классе.

Важно также использование обратной связи – реакции внешнего мира и других людей на твои действия, в том числе, вычисления. Умение использовать эту реакцию, найти у себя ошибку и попытаться ее исправить сегодня важнее, чем заведомая безошибочность. Подробнее об этом пойдет речь далее.

Современные базовые объекты. Детально мы рассмотрим их в основной части статьи. Сейчас лишь заметим, что это – основные объекты математики и информатики, при этом:

● они служат основой для всей математики;

● объекты математики бесконечного строятся из конечных объектов: свойства и рассуждения о бесконечных объектах основываются на свойствах конечных объектов и рассуждениях о них (конечно, этот “наивный конструктивизм” – лишь начало…).

Для вхождения в мир математики мы ставим перед детьми задачи построения дискретных (комбинаторных) объектов, удовлетворяющих заданным условиям. Условия эти могут быть логической (прежде всего – кванторной) комбинацией других, простейших, условий.

Реальный мир и обратная связь. Условие задачи может быть нарративом, историей о реальном, или “реальном” мире (как в “текстовых задачах” традиционного курса математики). Такая история может быть оформлена литературно как небольшой рассказ, или может быть просто взят подходящий фрагмент детской книги. Текст может содержать описание ситуации, с которой ребенок сталкивается в магазине, в кафе или на вокзале. Конечно, условие задачи может быть также просто техническим абстрактным описанием, но это обычно не так интересно для детей. Важной частью реального мира являются и явления естественных и математических языков, школьные расписания и индивидуальные планы.

Частью решения задачи является моделирование – построение математической модели, отождествление объектов, процессов и отношений, о которых идет речь в задаче, с математическими объектами, процессами и отношениями. Среди отношений и свойств могут быть числовые, о которых можно себе представить, что они могут быть измерены или сосчитаны, могут быть и логические (например, на автобусе нужно ехать до того момента, как появится возможность сесть на поезд, или необходимо понять, хватит ли денег на покупку).

К описанным задачам относятся, например, построение диаграммы роста (высоты) учеников в классе и ее изменение за год; подсчет количества домашних питомцев разного вида у учеников; распределение суммы очков, выпавших на трех костях; составление бюджета вечеринки для одноклассников; планирование расписания экскурсии в соседний город; составление сметы для закупки школьного компьютерного класса.

Числа, отношения, зависимости между ними остаются важнейшим элементом математического взгляда на мир. При этом происходит радикальное изменение приоритетов. В традиционной школе для массового ученика этап моделирования не был центральным, модель всегда создавалась по стандартным шаблонам: “путь есть скорость на время”, “расстояния для пешеходов надо сложить”. Ученику только надо было уметь распознавать, какой шаблон выбрать из небольшого количества стандартных шаблонов. В крайнем случае модель построит “начальство” (учитель), а тебе нужно только решить уравнение, точно все вычислить. В школе XXI века этап вычислений может быть целиком передан компьютеру, а основная образовательная нагрузка переместится именно на стадию моделирования [13, 14]. Разнообразие моделируемых ситуаций при этом может быть существенно увеличено, в том числе и за пределы тех ситуаций, которые обычно рассматривались в школьном курсе физики.

Построение, использование и обсуждение структур дискретной математики и их свойств дают возможность учащимся строить модели в социально-гуманитарных областях. Отношения на цепочках (конечных последовательностях) дают ученику и учителю четкую систему понятий, фактически постоянно используемую в лингвистических и, например, исторических курсах. Разнообразные циклы возникают в курсе “окружающий мир”: времена года, фазы Луны, недельный цикл. Древесные структуры (конечные графы) используются в биологии для классификации, в том же “окружающем мире” и в курсе истории для построения генеалогических деревьев, в том числе семейных деревьев самих учеников. В самой же информатике, в программировании цепочки описывают программный код и ход конкретного вычисления, мешки – возможные выборы.

Наконец, обратим внимание, что наряду с математическими моделями реальности в курсе постоянно используются реальные представления математических объектов. Более того, эти представления и являются объектами математической деятельности ученика. Написанная на бумаге цепочка цифр и есть (натуральное) число.

Обратная связь. Исключительно важно не заканчивать решение задачи на получении числового ответа – такая работа подобна движению робота, который не имеет обратной связи с реальностью при выполнении алгоритма. Полученный в процессе моделирования результат необходимо проверить на математическое и жизненное правдоподобие – сопоставить с конкретной реальностью. Соотнесение получаемых результатов с условием задачи, с реальностью и контекстом, умение усомниться в своих вычислениях и рассуждениях образуют комплекс умений, важных не только для математики. Соображения о порядке величины (может ли количество учеников в школе быть восьмизначным числом), о целочисленности (классические “два с половиной землекопа”) и о делимости (если по условию все дети класса стояли парами, их должно быть четное число) обеспечивают ученику ту самую обратную связь, которая помогает скорректировать неверные рассуждения в ходе решения задачи, найти свою ошибку. Это позволяет повысить безошибочность решений более адекватным современному миру способом, чем традиционная “отработанность алгоритмов вычислений” без обратной связи. Учитель помогает ученикам изобретать и следовать различным стратегиям, которые помогают им находить ошибки и несоответствия и в математическом контексте, и в более широком круге задач.

Новизна. Как показывает практика работы математических классов в СССР и в России, новизна и посильная трудность задач являются важнейшим мотивирующим фактором для самых разных детей [15].

Следуя П.Я. Гальперину [16] в его интерпретации исследования Вольфганга Кёлера когнитивного поведения животных [17], мы отмечаем следующие характерные особенности самостоятельно изобретенного решения в сравнении с решением задачи по заранее известному алгоритму:

● гибкость – найденное решение легко переносится в другие, чем-то похожие, ситуации: обезьяна, догадавшись сама использовать палку, чтобы достать банан, и далее, при решении других задач пробует использовать палку;

● обобщаемость и модифицируемость – П.Я. Галь- перин приводит пример, когда обезьяна в очередной раз за отсутствием палки использует одеяло, скатав из него валик; другая же обезьяна, которая не изобрела перед этим использование палки, а подсмотрела это у других, не догадывается использовать одеяло таким образом;

● эмоциональная значимость – человек гордится своим изобретением, самостоятельно найденным решением, помнит о нем, получает удовольствие от процесса решения в дальнейшем. Тот факт, что опыт самостоятельного открытия стимулирует поисковую активность в дальнейшем, отмечается и другими исследователями, например, [18].

Одним из подтверждений важности (Proof of Concept) “педагогики неожиданных задач” служит для нас олимпиада Кенгуру [19, 20] – конкурс для учеников 1–11 классов, который проводится в России с 1994 г. Учащимся предлагается 30 задач разной сложности, не похожих на обычные школьные задачи, которые они решали в школе до этого. Необычность задач часто дает возможность и неуспешному в школьной математике ребенку получить высокий результат в олимпиаде. Это привлекает детей, их родителей и учителей, поэтому количество участников олимпиады растет год от года – в 2022 г. в конкурсе приняло участие почти 350 тысяч учеников из 72 регионов России. В международном конкурсе Кенгуру ежегодно принимает участие больше 6 млн. школьников [21].

Систематичность. Наглядные объекты дискретной математики, суждения о них и действия с ними образуют фундамент математики и информатики и, соответственно, основу нашего курса для начальной школы. Практически все введенные понятия, структуры и операции получают развитие в курсе основной школы, используются и в дальнейшем, в том числе в профессиональной деятельности человека XXI века – подобно тому, как в XIX веке профессионалами использовались числа и десятичные дроби.

Помимо этого, мы формируем:

● систему рассуждений, обобщающих отдельные примеры;

● “большие идеи” как ориентацию в мире, в том числе – общие методы решения задач.

Концепция большой идеи (Big Idea) возникла в естественно-научном образовании как оппозиция к “горé фактов” [22]. Большая идея – это ориентационная часть представления человека о мире, без которой представление в целом, поведение в мире становятся другими. Большая часть “навыков XXI века” является более древней и присущей образованному человеку системой, чем остальная часть результатов образования XX века. К таким навыкам относится само умение учиться, понимать другого человека, ставить цели и анализировать неудачи и т.п. Ориентация в мире меняется быстрее и особенно быстро – сейчас. Все более необходимыми для ориентации становятся большие идеи цифровой грамотности [23, 24]. Способность использовать ориентацию вместе с формирующейся в математике и информатике способностью решать совершенно новые задачи, составляют основу пре-адаптивности [25].

Общий метод, большую идею невозможно “выучить”, можно лишь накапливать ситуации, где они применяются. При этом ученик, который освоил общий метод в применении к некоторому классу ситуаций, начинает “видеть” решение для очередной ситуации, которая оказывается для него не новой. Тогда желательно опять перейти к новому материалу. Однако, если решение похожих задач, демонстрация мастерства в таком решении остается фактором положительной мотивации, такими задачами можно эту мотивацию подпитывать.

В следующих разделах статьи параллельно с введением основных математических структур начальной школы (почти все они появляются уже в первом классе) мы даем примеры начальных упражнений и задач. Эти примеры направлены, в частности, на иллюстрацию тезиса о сочетании постоянной новизны с систематичностью и большими идеями. Примеры взяты из двух линеек: курса “Математика и информатика 1–4” [26], рассчитанного на 4 или даже 5 ч в неделю и курса “Информатика” [9], рассчитанного на 1 ч в неделю. Авторский коллектив курса “Математика и информатика 1–4” – А.Л. Семенов, М.А. Посицелькая, С.Е. Посицельский, Н.А. Сопрунова, И.А. Хованская, Т.В. Михайлова, Т.А. Рудченко. Авторский коллектив курса “Информатика 1–4” – А.Л. Семенов, Т.А. Рудченко. Оба курса создавались внутри одной авторской концепции и под общим руководством А.Л. Семенова, тем не менее, и программы курсов, и объемы курсов различаются, над линейками работали разные авторские коллективы, поэтому подходы и реализации конкретных тем различаются. В дальнейшем описании мы время от времени указываем, к какому именно курсу относятся те или иные моменты.

4. ОСНОВНЫЕ СТРУКТУРЫ

Еще до школы ребенок сталкивается с упорядоченными и неупорядоченными совокупностями, циклами и таблицами.

Упорядоченной является цепочка событий: одно событие следует за другим. Слова в речи идут одно за другим: их можно вычленять в устной речи, преобразуя ее в письменную – получатся цепочки букв, которые образуют слова, цепочки слов образуют предложения и т.д.

Список покупок – пример языковой цепочки. А вот сами покупки, лежащие в тележке, уже не упорядочены. Среди покупок могут быть два батона, четыре банана и десяток яиц, три пакета молока. При этом при покупке мы скорее всего считаем, что все батоны одинаковы, все яйца в упаковке одинаковы, а вот яйцо и батон – это разные объекты.

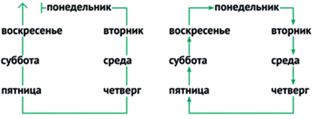
Смена дня и ночи, дни недели и времена года в жизни ребенка образуют длинную периодическую цепочку и тесно связанный с ней цикл. Наконец, таблицы в жизни современных детей возникают очень рано как способ структурировать режим дня, присутствуют в расписаниях поездов и автобусов, поликлиник и магазинов, с которыми ребенок сталкивается в повседневности. Часто таблицы возникают в тех или иных мобильных и компьютерных приложениях для дошкольников.

Мы в наших курсах математики и информатики для начальной школы определяем все эти структуры на визуальных примерах – именно так ребенок обычно выучивает новые слова. При этом мы комментируем примеры, например: “в цепочке обязательно указывают начало и конец” или “в цикле нет первого и последнего элемента”. Это создает плавный переход от бытового мышления к научному, о котором писал Л.С. Выготский [27].

Важными объектами являются пустые структуры (пустой мешок, пустая цепочка, пустой цикл). Существует только одна пустая структура каждого вида.

Ключевым для нас выступает вопрос об изоморфизме или одинаковости структур.

У всех объектов, атомарных и более сложных, могут быть имена. Именем обычно выступает цепочка символов – букв русского или латинского алфавита и цифр.

5. ЭЛЕМЕНТАРНЫЕ (АТОМАРНЫЕ) ОБЪЕКТЫ

В школе символами, элементами цепочек, мешков и циклов могут быть:

● телесные объекты – бусины разных форм и цветов – из дерева или пластика;

● карточки с рисунками, в частности и с нарисованными бусинами;

● разнообразные графические объекты на бумаге – на отдельных листах или в тетради;

● разнообразные графические объекты на экране – в цифровой среде.

Из элементов можно составлять цепочки и мешки, например, нанизать вырезанные из картона бусины на шнурок. Реальные объекты и графические образы на экране легко перемещать руками или мышкой. Из мешка можно что-то вынимать и туда класть. Цепочки можно перемещать целиком. В цепочку на шнурке можно что-то добавлять или убавлять только в начале или в конце – на концах шнурка. С цепочкой карточек, выложенных в ряд на столе, можно обходиться более свободно, например, можно договориться, что карточки в цепочке можно менять местами, как угодно; это означает, что мы имеем дело не с цепочкой, а с мешком карточек. Такие же договоренности можно применять и к элементам в цифровой среде.

Элементами, с которыми работают дети при решении большинства задач курса, являются бусины, монеты, фигурки (картинки), цифры и символы различных алфавитов, знаки дорожного движения и пр. Будем называть их атомарными объектами.

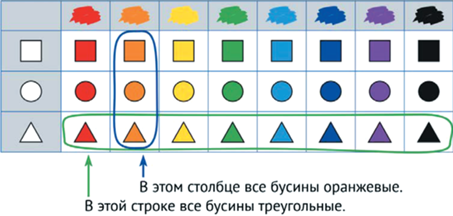
Бусины бывают восьми цветов (цвета радуги и черный) и трех форм: треугольные, круглые и квадратные. Две бусины являются одинаковыми, если у них совпадают цвет и форма. По размеру бусины не различаются (см. рис. 1).

Рис. 1.

Бусины, используемые в курсе.

Две монеты являются одинаковыми, если у них совпадает номинал. Иногда монеты изображаются реалистично, картинкой, а иногда схематично – как кружок с числом внутри.

Фигурки могут быть разными, их список не ограничен. В курсе “Математика и информатика” фигурки считаются одинаковыми, если существует движение плоскости, переводящее одну фигурку в другую. Ученик может приклеивать фигурки в мешок не только вертикально (см. рис. 2).

Рис. 2.

Определение одинаковости для фигурок в курсе “Математик и информатика”. Здесь все фигурки считаются одинаковыми.

В курсе “Информатика” определение одинаковости для фигурок более узкое, но при этом и более универсальное: одинаковыми считаются только те фигурки, которые можно получить одну из другой параллельным переносом – в таком случае, скажем, для дорожных знаков не придется вводить новое определение одинаковости и для букв и цифр можно остаться на уровне этого определения, не вдаваясь в нюансы, сложные для первоклассников. В рамках такого определения на рис. 3 даны пары разных фигурок.

Рис. 3.

Определение одинаковости фигурок в курсе “Информатика”. Фигурки в этих парах считаются разными.

Кроме того, атомарными объектами являются символы: цифры, буквы, знаки препинания и даже иероглифы.

6. СВОЙСТВА, ОТНОШЕНИЯ, ВЫСКАЗЫВАНИЯ (УТВЕРЖДЕНИЯ), ДЕЙСТВИЯ

Мы считаем, что учителю, который работает с курсом в классе, полезно иметь в своем распоряжении сформированную систему понятий, которой он может пользоваться в своем внутреннем языке для описания ситуаций и процессов в решении задач – в частности и для того, чтобы использовать эти понятия при обсуждении с ребенком полученного им решения. Учащиеся могут постигать смысл этих понятий постепенно, на примерах.

Одновременно в работе и ученика, и учителя используются ключевые понятия, которые вводятся в учебнике последовательно и явно, и тоже на примерах. Мы исходим из того, что понимание того, о чем идет речь, возникает у ребенка быстро и в дальнейшем просто подкрепляется и расширяется при решении задач.

К ключевым понятиям относится, например, понятие о цвете бусины – одном из восьми. Общее же понятие о свойствах бусины, которыми бусина может обладать или не обладать, относится к внутреннему языку учителя.

Ключевым является отношение непосредственного следования между бусинами в цепочке: “эта желтая бусина следует за этой синей” – это мы показываем ученикам на примерах из листов определений учебника. Отношение усваивается при решении задач этого и следующих уроков.

Учащийся выполняет конкретные действия с объектами, например, соединяет одинаковые фигурки зеленой линией. Общее представление о действии, понятное учителю, постепенно формируется и у учащегося.

Общее понятие высказывания (утверждения), которое может быть истинным или ложным для некоторой системы объектов – это поначалу элемент внутреннего языка учителя. Понимание того, что все высказывания из условия задачи выполнены для данной цепочки – элемент работы учащегося. В некотором месте курса мы даем уже подготовленным ученикам понятия истинности и ложности утверждения и используем их при выделении в условии задачи отдельных высказывания – выписывая их каждое по отдельности и в условии явно формулировать требование о том, что все указанные утверждения должны принимать указанные значения (в большинстве своем истинные, но в некоторых задачах – и ложные тоже).

Пример высказывания, которое может быть истинным или ложным, показан на рис. 4.

Рис. 4.

Пример высказывания, которое может быть истинным или ложным.

В учебной ситуации ребенок обычно может сам быстро и надежно проверить, подходит ли созданный им объект под условия задачи. Свойства объектов мы, как правило, формулируем в виде набора утверждений. Эти утверждения могут включать в себя слова, связанные со структурой объекта и одинаковостью его элементов. Используются такие обороты, как:

● есть три разные бусины,

● нет трех одинаковых подряд,

● за каждой синей следует либо красная, либо снова синяя,

● перед треугольной бусиной идет красная.

Чтобы проверить выполнение всех условий, нужно против каждого утверждения поставить его значение. Если все значения окажутся истинными, задание выполнено верно.

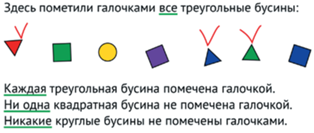
Особенное внимание авторы уделяют кванторным словам – “все”, “каждый”, “найдется”, “существует” и другим, смысл которых соответствует кванторам, используемым в математике: ∀, ∃. На рис. 5 даны несколько примеров их использования.

Рис. 5.

Пример использования кванторов в задаче.

Возможно использование квантора по подмножеству, заданному свойством (см. рис. 6).

Рис. 6.

Пример использования кванторов в задаче.

В случае, если объектов немного, утверждение с квантором легко проверить (см. рис. 7).

Рис. 7.

Пример использования кванторов в задаче.

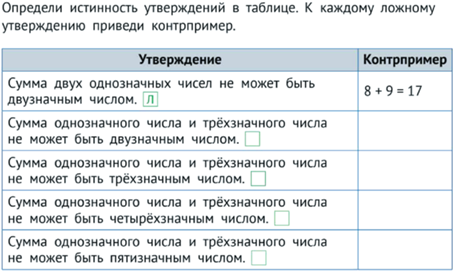
Если ложное утверждение касается объектов из некоторого класса, к нему можно привести контрпример (см. рис. 8).

Рис. 8.

Контрпримеры к ложным утверждениям.

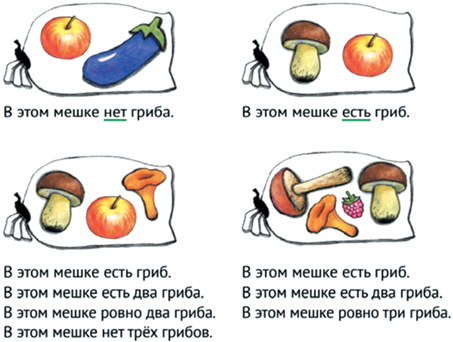
В русском языке не используются артикли, но есть достаточно много умолчаний, которые на математическом языке выражаются формулами с кванторами. Много внимания в нашем курсе уделено экспликации подобных умолчаний и обсуждению их с детьми. На рис. 9 приведены примеры истинных утверждений о мешках.

Рис. 9.

Примеры истинных утверждений с кванторами.

7. ЦЕПОЧКИ (ПОСЛЕДОВАТЕЛЬНОСТИ)

Примерами цепочек в окружающей жизни являются, например, последовательность событий и их запись – последовательность звуков устной речи и их письменная фиксация, последовательность ходов в игре и запись партии игры.

Цепочка, с одной стороны, является записью, моделью последовательности выборов. С другой стороны, создание, рисование цепочки – есть результат выборов очередного ее символа из мешка символов. Цепочка возникает при нанизывании объектов на нить; мы стараемся, чтобы дети хотя бы раз проделали это руками с телесными бусинами (см. рис. 10).

Рис. 10.

Появление цепочки бусин – процесс нанизывания на нитку.

Символически цепочка показана на рис. 11.

Рис. 11.

Пример цепочки бусин.

У цепочки есть начало, которое отмечается перекладинкой, и конец, который отмечается стрелочкой; для каждого объекта, кроме последнего, известен следующий за ним (см. рис. 12);

Рис. 12.

Определение следующего элемента в цепочке.

для каждого объекта, кроме первого, известен предыдущий перед ним (см. рис. 13).

Рис. 13.

Определение предыдущего элемента в цепочке.

Кому-то могут не понравиться смысловые повторы в словосочетании “предыдущий перед”, но мы перепробовали разные варианты и пришли к тому, что это наименьшее из зол.

Пустая цепочка – это просто веревка, на ней нет бусин, но отмечены начало и конец.

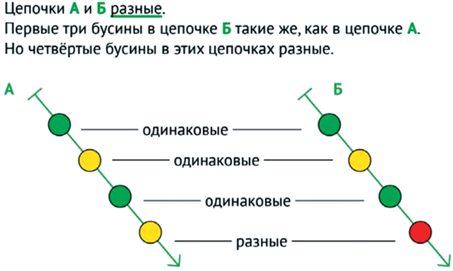
Две цепочки одинаковы, если совпадают почленно – первая бусина в одной цепочке такая же, как первая бусина в другой, вторая – такая же, как вторая в другой, и так далее; количество бусин в цепочках также должно быть одинаковым (см. рис. 14).

Рис. 14.

Определение разных цепочек – пример.

Все пустые цепочки одинаковы.

8. МЕШКИ (СОВОКУПНОСТИ)

Мешки – очень естественные математические объекты, по крайней мере, для конечной математики. С точки зрения работы с физическими объектами, мешки более естественны, чем множества. Одно из математических названий для мешка – это мультимножество, т.е. множество, в которое каждый элемент входит с той или иной кратностью. Чтобы продемонстрировать детям мешок, нужно взять в руки прозрачный полиэтиленовый пакет и положить в него какие-либо предметы. Если мешок потрясти, объекты внутри него переместятся, поэтому про мешок мы знаем лишь, что там лежит, никакого порядка на элементах мешка не предусмотрено.

Иногда мешки и вправду похожи на мешки, а иногда больше напоминают коробки. Иногда мешок принимает форму кошелька, а иногда это просто контур, нарисованный вокруг фигурок (см. рис. 15).

Рис. 15.

Определение одинаковых мешков.

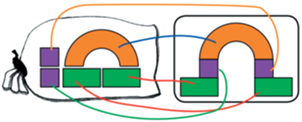
Мешки называются одинаковыми, если между ними можно установить взаимно-однозначное соответствие, при котором в пары объединены одинаковые объекты. Дети реализуют такие соответствия, соединяя пары одинаковых фигурок линиями. Установить одинаковость мешков сложнее, чем одинаковость цепочек – непонятно, с чего начать соединение в пары, легче запутаться (см. рис. 16).

Рис. 16.

Сравнение мешков, пример.

Если в мешке лежат бусины, удобно сравнить количество бусин каждого вида. Для этого можно использовать так называемую таблицу мешка (см. рис. 17). В такой (одномерной) таблице в верхней строке – “шапке” – представлены все виды бусин, имеющиеся в мешке.

Рис. 17.

Пример таблицы мешка.

Конечно, в курсе есть много разнообразных задач, использующих одинаковость мешков – помимо прямого сравнения двух мешков, предлагается найти два одинаковых среди большого количества мешков, найти все пары одинаковых, построить два одинаковых мешка (телесных или нарисовать), достроить мешки так, чтобы они стали одинаковым и пр. В качестве сложной линейки задач предлагаются задачи, в которых требуется изменить ровно один объект в одном мешке так, чтобы на картинке появились два одинаковых мешка (см. рис. 18).

Рис. 18.

Пример сложной задачи об одинаковых мешках.

Самой естественной операцией над мешками является сумма (обобщение суммы натуральных чисел): “сложить” два мешка – это действительно сложить их содержимое в один. Две других важных операции над мешками – это объединение (максимум) и пересечение (минимум). Конечно, мешки с этими операциями образуют решетку. Также ясно, что эти операции естественно применять не только к двум мешкам, но к произвольному мешку мешков.

Только что описанные операции над мешками показывают, что в мешках могут лежать не только атомарные объекты, но и структуры – мешки, цепочки, слова (цепочки букв). Работа с мешком слов дает возможность точно сформулировать стандартное задание из курса русского языка “вставь пропущенные буквы” Возможная точная формулировка такая: “напиши в каждом окне одну букву так, чтобы получилось слово из словаря”. При этом, конечно, должно быть понятно, о каком словаре идет речь. Словарь может быть стандартным школьным, бумажным или электронным, словарем, создаваемым самим учащимся, или имеющимся в самой задаче или в конце учебника и т.п.

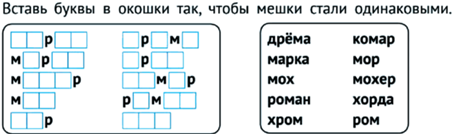
В нашем контексте возникают сложные и содержательные задачи на установление соответствия между двумя мешками цепочек, которые нужно сделать одинаковыми (см. рис. 19).

Рис. 19.

Пример задачи об одинаковых мешках слов.

Эта задача хороша тем, что допускает простейшие ходы рассуждения и разделения на подзадачи. Например, для начала можно заметить, что в мешке только одно слово из четырех букв и разобраться со словами из трех букв; слов, начинающихся на букву р, в мешке только два и т.д. Этими соображениями можно делиться с товарищами, осваивая при этом математическую речь, увеличивая запас эвристических приемов.

Заметим, что в таких задачах мы не предполагаем, что дети знают значения используемых слов. Задача – формальная, требующая только использования математического определения. При этом совсем не плохо, если кто-то из учеников заинтересуется каким-то словом и посмотрит его значение в словаре сам или с помощью учителя. В методических комментариях мы часто напоминаем о такой возможности. Кроме того, в курсе есть отдельный цикл задач, для решения которых ребенку необходимо найти указанные слова в толковом словаре и понять их значение, чтобы затем оценить истинность высказывания, данного в задаче. Пример задачи приведен на рис. 20.

Рис. 20.

Пример задачи, которой нужно использовать толковый словарь.

В мешке, конечно, могут лежать числа (цепочки цифр). Все числа, лежащие в мешке, можно сложить или перемножить. При этом коммутативность и ассоциативность этих операций закладываются непосредственно в определение – числа, лежащие в мешке, точно не упорядочены. С другой стороны, эти свойства получают содержательную интерпретацию. Например, можно попросить детей найти сумму мешка из четырех троек и мешка из трех четверок и обсудить, почему эти суммы равны. Здесь необходим переход к другому определению умножения – через площадь соответствующего прямоугольника (см. рис. 21).

Рис. 21.

Прямоугольники на сетке.

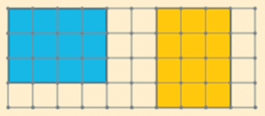
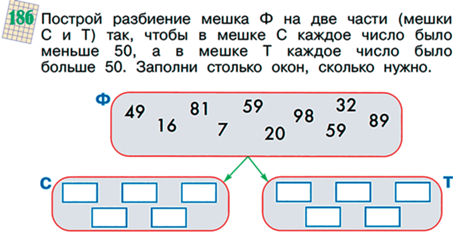
В современном мире задача сложения нескольких чисел встречается даже чаще, чем задача сложения пары чисел – покупки в магазине, зарплаты, количество посетителей редко встречаются парами, скорее складываются большие массивы таких данных. Встречаются и задачи, когда нужно сравнить суммы без необходимости их вычисления. Работа с мешками чисел позволяет нам легко формулировать такие задачи в курсе (см. рис. 22).

Рис. 22.

Задача о мешках чисел.

Подобные задачи также дают простор для рассуждений. Например, можно вычеркивать одинаковые числа в мешках – это действие влияет на сумму каждого из мешков, но не влияет на разницу этих сумм. Оставшиеся числа также можно не складывать, а сравнивать: если одно число из первой суммы больше на 9, а другое меньше на 1, значит, первая сумма больше на 8. Можно, вычеркивая в двух мешках близкие по величине числа, ставить разность этих чисел рядом с мешком, в котором лежало большее. Конечно, вычеркивание чисел (стирание, вынимание чисел из мешка и т.п.) проще делать в цифровой среде, чем на бумаге.

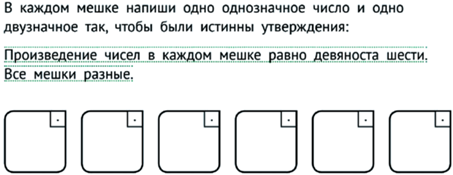
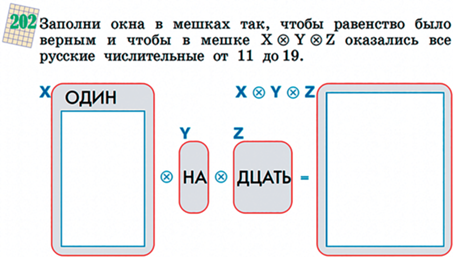
Язык мешков позволяет легко формулировать переборные арифметические задачи, в которых неважен порядок слагаемых. Так, например, можно познакомить детей с гипотезой Варинга и теоремой Лагранжа (см. рис. 23).

Рис. 23.

Гипотеза Варинга и теорема Лагранжа в задаче курса.

Конечно, очень важное и необходимое применение числовых мешков – это моделирование разложения чисел на множители. Можно перебирать все разложения или задавать те или иные ограничения на сомножители, пример приведен на рис. 24.

Рис. 24.

Пример задачи о разложении числа на множители.

И, конечно, естественно сопоставить число с мешком, где все числа простые, а произведение мешка равно данному числу – это мешок разложения числа на простые множители. Тогда произведению чисел будет соответствовать операция суммы двух таких мешков, а НОД и НОК будут получаться как минимум и максимум (объединение и пересечение) двух таких мешков.

9. ТАБЛИЦЫ

Поучительно обратить внимание на место таблиц в традиционной школе. С одной стороны, они там очевидно используются – это таблицы сложения и умножения, разнообразные таблицы в курсах русского и иностранного языка, в старших классах используется великое достижение человечества – таблица Менделеева. Школьное расписание, школьный дневник и журнал – это таблицы.

Однако несмотря на постоянное использование таблиц, их “не проходят” в школе как самостоятельный математический объект. Таблица оказывается чем-то вроде тетради, которую не имеет смысла “проходить” в математике. Причина, видимо, в том, что таблица как-то не умещается в строгую последовательность постижения арифметики. Но при этом школа исходит из того, что ученики откуда-то про таблицу знают, умеют ею пользоваться.

Таблица состоит из цепочки имен строк (самый левый столбец), цепочки имен столбцов (самая верхняя строка) и клеток. Выражаясь математически, таблица – это отображение, ставящее в соответствие паре “имя строки, имя столбца” содержимое клетки, стоящей на пересечении этой строки и этого столбца. Раньше мы упоминали одномерные таблицы.

К примеру, в таблицу удобно внести все виды бусин, которые встречаются в курсе (см. рис. 25).

Рис. 25.

Двумерная таблица мешка бусин.

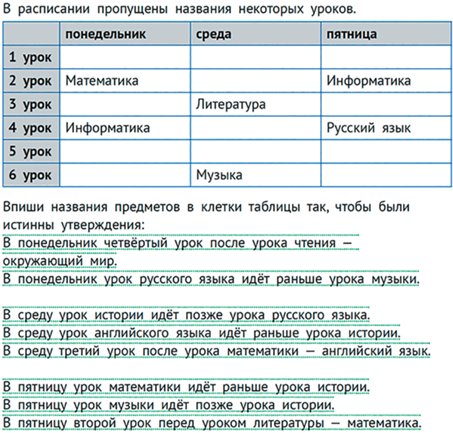
Школьное расписание является таблицей, где имена строк – это номера уроков, а имена столбцов – это дни недели.

На рис. 26 приведен пример задачи на составление расписания.

Рис. 26.

Пример задачи на составление расписания.

Возможны и более приближенные к жизни условия, например: “…каждый день есть урок русского языка”, “…есть ровно один урок музыки в неделю”, “…такие-то уроки идут раньше таких-то” – подобные требования бывают в СанПиНах. Могут быть и ограничения, связанные с днями работы учителя физкультуры или музыки, которые приходят в школу не каждый день.

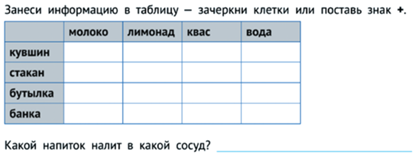
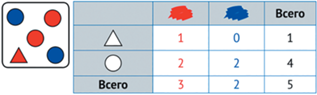
Классическое использование таблиц – решение так называемых логических задач, которых дано несколько утверждений. Пример приведен на рис. 27.

Рис. 27.

Пример традиционной логической задачи.

Требуется выяснить, какой напиток налит в какой сосуд. Самый удобный способ структурировать такую информацию – внести ее в таблицу, пометив разным образом высказывания о жидкости в сосуде, которые являются истинными знаком “+” и зачеркиванием те, которые являются ложными (см. рис. 28).

Рис. 28.

Пример решения традиционной логической задачи с помощью построения таблицы.

Новизна этой задачи для ученика может состоять в том, что он использует помимо явных высказываний: “что-то в чем-то”, еще и высказывания с отрицанием, и два высказывания, объединенных в одно предложение; высказывания о пространственном расположении, в том числе, с использованием терминов “рядом”, “между”, хорошо, если у ученика возникнет вопрос, относящийся к линейности расположения сосудов. Сложностью при решении этой задачи может оказаться рассмотрение высказывания: “стакан находится рядом с банкой и сосудом с молоком”. Эквивалентно ли это высказывание такому: “стакан находится рядом с банкой и рядом с сосудом с молоком”? А такому: “стакан находится рядом с банкой и стакан находится рядом с сосудом с молоком”? Почему мы думаем, что стакан не находится рядом с собой? В связи с трудностью использования союзов “и”, “или” в естественном языке, в некоторых вариантах нашего курса мы избегаем союзов и формулируем так: “все высказывания из данного мешка истинны” и “среди высказываний данного мешка есть истинные”.

Примеры использования таблиц для нахождения ВСЕХ объектов, удовлетворяющих какой-то системе условий, см., например, в [28] и [29].

10. ЦИКЛЫ

В цикле у каждого элемента есть предыдущий и следующий. У цикла нет начала и нет конца. Направление от предыдущего к следующему указывается стрелками (см. рис. 29).

Рис. 29.

Определение цикла.

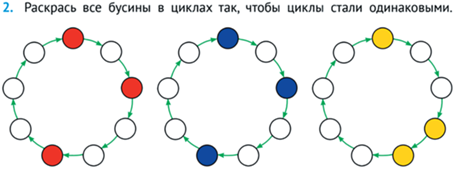
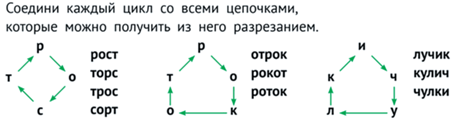
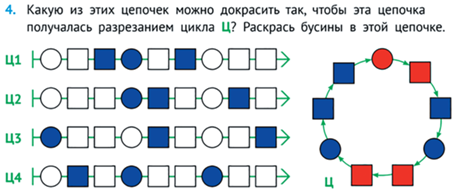
Цикл можно разрезать – получится цепочка. Два цикла одинаковы, если их можно разрезать так, чтобы получилось две одинаковые цепочки (см. рис. 30).

Рис. 30.

Определение одинаковых циклов.

В случае циклов даже задача создания двух или трех одинаковых объектов может быть вполне сложной и содержательной (см. рис. 31).

Рис. 31.

Пример непростой задачи о циклах.

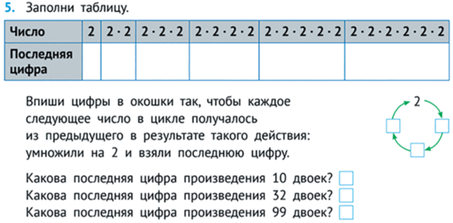
Циклы имеют разнообразные математические приложения: периодические последовательности, арифметику остатков (см. рис. 32).

Рис. 32.

Задача о периодической последовательности.

Эта задача является одной из вводных в экспериментальную математику. Заполняя таблицу (в нее можно добавить верхнюю строчку, в которую мы вписываем сами произведения – их можно найти с помощью калькулятора), мы видим, что последняя цифра в произведениях двоек повторяется. Нарисованный цикл подталкивает нас к идее доказательства. Учитель может в ходе решения задачи, или после него, предложить другие задачи на ту же тему, например, кто-то из учеников отворачивается (закрывает глаза), на доске написаны два числа, их цифры, кроме последних, закрываются. Может ли ученик найти последнюю цифру произведения? Почему она будет такой?

Задача становится вполне посильной, если ученики сами изобрели тот или иной алгоритм умножения многозначных чисел, например, древний индийский алгоритм умножения “диагоналями”, но обсуждение этого вопроса увело бы нас от основной темы данной статьи.

11. ДЕРЕВЬЯ¹¹

Деревья – это конечные ориентированные графы, где в одну вершину (корень) не идет ребер, а в любую другую ведет ровно одно ребро. В вершинах дерева могут стоять любые элементы, которые до этого использовались в курсе для построения цепочек и мешков: бусины, фигурки, буквы, слова и пр. По аналогии с цепочками начало (корень) дерева, отмечается перекладинкой. Каждая вершина такого дерева имеет ровно одну предыдущую (если она не лежит на первом уровне дерева) и конечное число следующих. Если следующих – 0, вершина называется листом. Листья дерева отмечены выходящими из них стрелками – так же, как отмечен конец цепочки. Цепочка тоже является деревом – у которого каждая не последняя вершина (бусина) имеет ровно одну следующую.

Путь в дереве – это цепочка, идущая от корня дерева к листу.

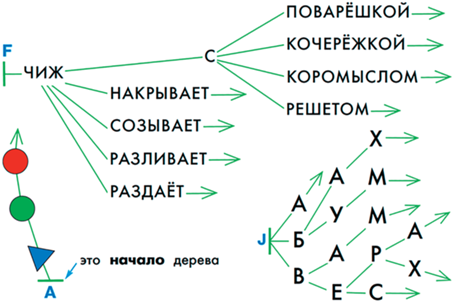
Примеры деревьев, имеющих лингвистический смысл, приведены на рис. 33: идя по пути в дереве, мы читаем осмысленную фразу или слово.

Рис. 33.

Определение дерева на примерах в курсе “Информатика”.

Вопрос об одинаковости деревьев авторы посчитали слишком сложным и объемным для начальной школы, поэтому в курсе он не обсуждается.

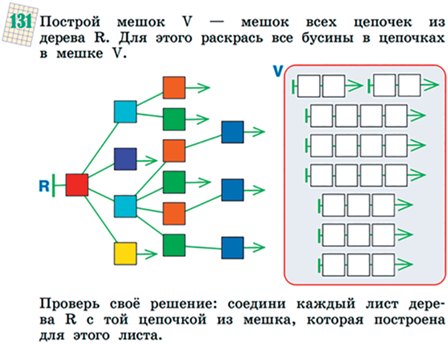
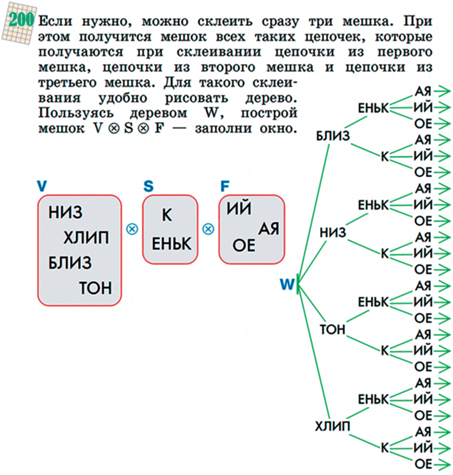
На деревьях определена операция перехода от дерева к мешку путей, состоящему изо всех цепочек, которые можно прочитать на путях дерева (см. рис. 34).

Рис. 34.

Задача о построении всех путей дерева.

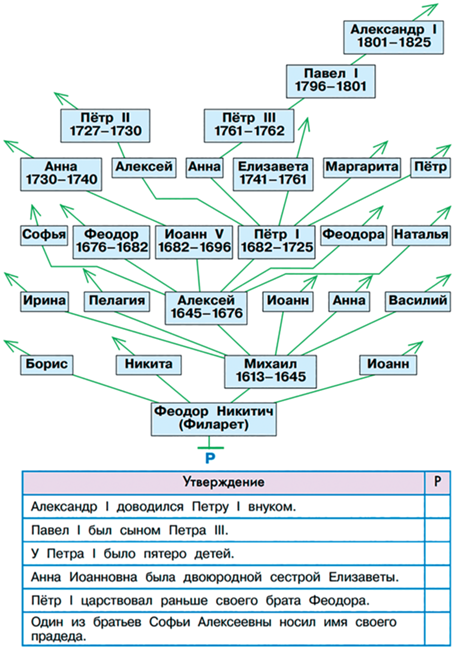
С деревьями дети будут встречаться на различных уроках, пример на рис. 35 – деревья предков и деревья потомков.

Рис. 35.

Работа с деревом потомков.

Используются такие деревья и на уроках биологии – различные классификации, и построенные на их основе определители.

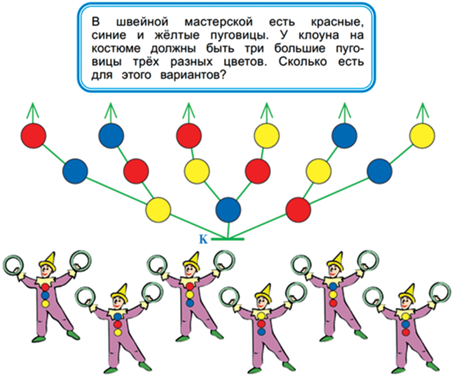
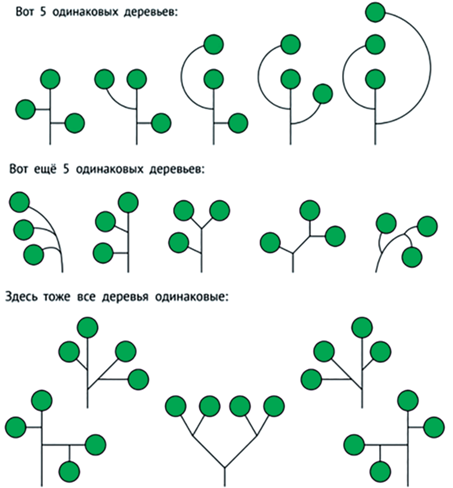
Построение дерева помогает решить задачу о переборе всех вариантов – для этого строим дерево и затем выписываем все его пути, считаем, сколько разных цепочек получилось (см. рис. 36).

Рис. 36.

Пример задачи о поиске всех вариантов.

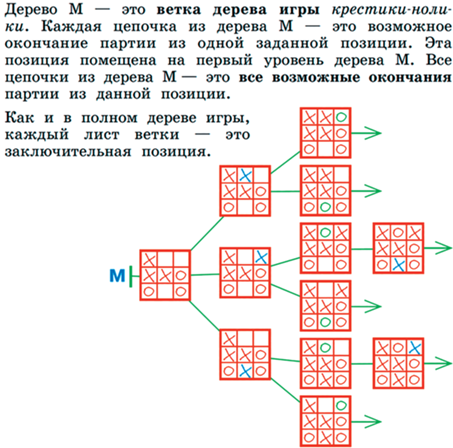
Также полезно построить дерево при исследовании игр с полной информацией и построении выигрышной стратегии (см. рис. 37).

Рис. 37.

Пример ветки из дерева игры крестики-нолики.

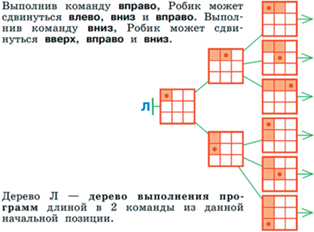
Дерево позволяет исследовать вопрос о возможных позициях Робика после выполнения, скажем, двух команд (см. рис. 38).

Рис. 38.

Пример дерева выполнения команд длиной в 2 команды.

12. ДВОИЧНЫЕ ДЕРЕВЬЯ²²

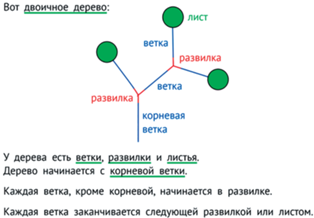
Один из вариантов темы деревья в наших курсах построен на использовании только двоичных деревьев. Используемая при этом система определений несколько отличается от рассмотренной выше. Двоичное дерево состоит из корня, веток, развилок и листьев. Пример на рис. 39.

Рис. 39.

Определение двоичного дерева в курсе “Математика и информатика”.

Из корня выходит строго одна ветка. Каждая ветка ведет в развилку или ведет в лист. Из каждой развилки выходит ровно две ветки – левая и правая.

Деревья можно по-разному изгибать, при этом они остаются такими же (пример на рис. 40).

Рис. 40.

Определение одинаковости двоичных деревьев.

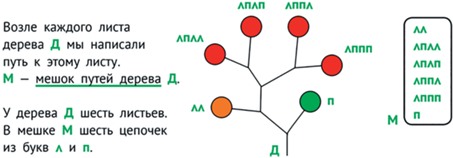
Путь к листу от корня может быть задан последовательностью левых и правых выборов во всех развилках – цепочкой из букв Л и П. Эту цепочку мы называем именем соответствующего листа. Например, если мы из корня идем влево и на второй развилке снова влево и приходим к листу, то этому листу мы даем имя ЛЛ (см. рис. 41).

Рис. 41.

Определение мешка путей двоичного дерева.

Имея мешок имен всех листьев, можно нарисовать все дерево. Можно предложить нескольким ученикам построить свои деревья, располагая одним и тем же мешком: могут ли у них получиться разные деревья? Если такое случилось, предложим детям обменяться рисунками и объяснить друг другу, как они действовали. Для сравнения деревьев можно покрасить листы с одинаковыми именами в один цвет и т.п. В конце концов, вероятно, ошибка найдется и выяснится, что правильное дерево только одно.

Возникает проблема: объяснить, доказать, что из одного мешка всегда получатся одинаковые деревья. В попытке разобраться с этой проблемой можно начать с очень простых мешков, например, состоящих из однобуквенных и двухбуквенных имен (см. рис. 42).

Рис. 42.

Подготовка к понимаю доказательства того, что из одного мешка всегда получатся одинаковые (двоичные) деревья.

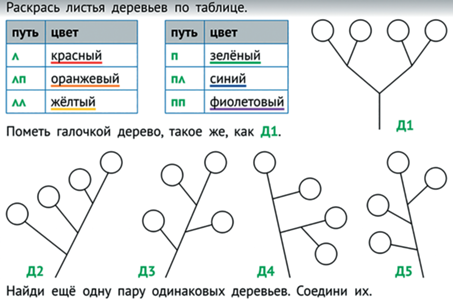
Можно попытаться при построении деревьев применить уже известный детям метод “разделяй и властвуй”. А именно, разделить мешок на две части: в одном мешке все имена начинаются с буквы Л, в другом – с буквы П. Достаточно быстро в обсуждении у кого-то из детей возникает идея в этих двух мешках у всех имен (цепочек) отбросить первую букву. Теперь можно построить для каждого из этих мешков дерево. Кажется, мы начинаем понимать, почему из одного мешка у всех получается одно и то же дерево?

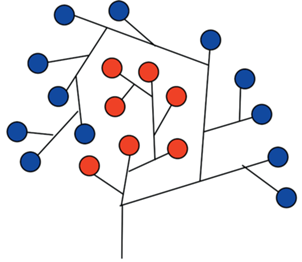
Если дерево имеет сложную форму, не всегда просто увидеть, где у него левая часть, а где правая (см. рис. 43).

Рис. 43.

Раскраска левой и правой части двоичного дерева.

На этой картинке листы левого поддерева раскрашены красным, листы правого поддерева – синим цветом.

Двоичные деревья также имеют глубокое арифметическое приложение. Дети не всегда понимают смысл заключения выражения в скобки. Вот пример вычисления:

27 + (45 : 9) =

1) 45 : 9 = 5

2) 27 + 45 = 72

В чем причина ошибки? Ребенок не понимает, что результат первого действия нужно использовать во втором. Для разрешения этой проблемы полезно обвести эту пару овалом, дополнив скобки сверху и снизу:

А затем заменить овал результатом первого действия и вычислить общий результат.

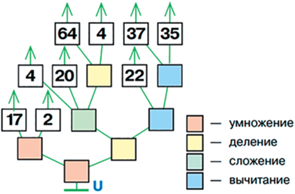
Двоичные деревья отлично описывают этот процесс выполнения действий с двумя аргументами. Для того, чтобы найти значение выражения, мы “спариваем” числа, входящие в выражение, в определенном порядке (см. рис. 44).

Рис. 44.

Дерево вычисления арифметического выражения.

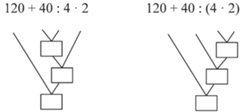
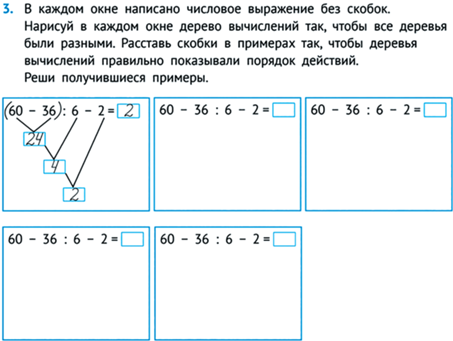
Перебирая двоичные деревья, мы можем параллельно перебрать все способы расставить скобки в данном числовом выражении (см. рис. 45).

Рис. 45.

Пример задачи о вычислении значения арифметического выражения при помощи двоичного дерева.

Эти задания перекликаются с часто встречающимися в сборниках занимательных задач заданиями расставить скобки в выражении так, чтобы оно приобрело данное значение (см. рис. 46).

Рис. 46.

Традиционная занимательная задача о расстановке скобок.

Если раньше дети могли решать такую задачу лишь по наитию, теперь они, вообще говоря, могут системно перебрать все расстановки скобок и доказать возможность или невозможность получения данного значения выражения.

Наконец, заметим, что бинарность ассоциативных и коммутативных операций, таких, как сложение и умножение, не является естественной необходимостью. В одной скобке (овале) может находиться несколько слагаемых или сомножителей – в таком случае, конечно, нужно использовать не двоичное дерево (см. рис. 47).

Рис. 47.

Пример небинарного дерева вычисления значения арифметического выражения из курса “Информатика”.

13. ОПЕРАЦИИ С ЦЕПОЧКАМИ И МЕШКАМИ

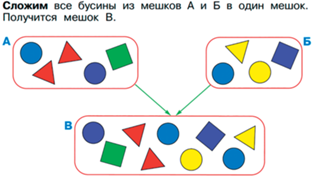
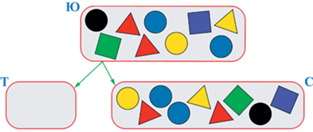
Ссыпание мешков – аналог операции объединения для множеств. Два мешка можно ссыпать в один – получится новый мешок (см. рис. 48).

Рис. 48.

Определение операции ссыпания мешков.

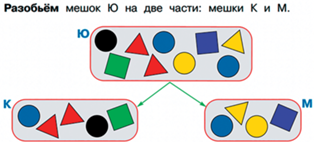
Мешок можно разбить на части (см. рис. 49).

Рис. 49.

Определение операции разбиения мешка на части.

При этом часть может оказаться и пустой (см. рис. 50).

Рис. 50.

При разбиении мешка некоторые части могут быть пустыми.

Введенные таким образом операции над мешками позволяют формулировать большой спектр понятных детям задач, которые могут выходить и за рамки собственно курса информатики – это и работа с числами, и с языковыми структурами (буквами, словами) (рис. 51).

Рис. 51.

Задача о разбиении на части мешка чисел.

Операция приписывания (склеивания) цепочек – важный для начальной школы пример некоммутативной (не похожей на сложение и умножение) операции. Две цепочки можно склеить – получится новая цепочка. Если порядок цепочек при склеивании поменять – получится другой результат (см. рис. 52).

Рис. 52.

Определение операции приписывания (склеивания, конкатенации) цепочек. Некоммутативность.

Если одна из двух цепочек, которые мы склеиваем, – пустая цепочка, в результате склеивания получится вторая цепочка (см. рис. 53).

Рис. 53.

Определение операции приписывания (склеивания, конкатенации) цепочек. Склеивание с пустой цепочкой.

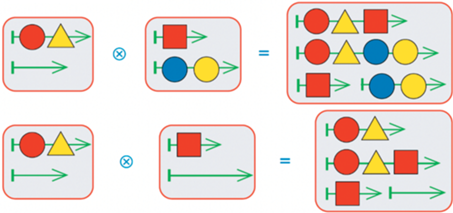
Операция склеивания мешков цепочек полезна при решении комбинаторных и лингвистических задач (см. рис. 54).

Рис. 54.

Определение операции приписывания (склеивания, конкатенации) мешков цепочек.

Введение (в курсе “Информатика” 3 класса) и использование операции склеивания мешков цепочек позволяет объяснить в точных, математических терминах и одновременно сделать наглядными правила курса русского и иностранного языка, например, относящиеся к словоизменению и словообразованию (см. рис. 55).

Рис. 55.

Пример задачи о склеивании мешков слов – основы и падежные окончания.

Еще один пример – из морфологии – показан на рис. 56.

Рис. 56.

Пример задачи на склеивание трех мешков – корни, суффиксы и окончания.

И даже из этимологии (см. рис. 57).

Рис. 57.

Пример задачи на склеивание трех мешков – порождение русских числительных второго десятка.

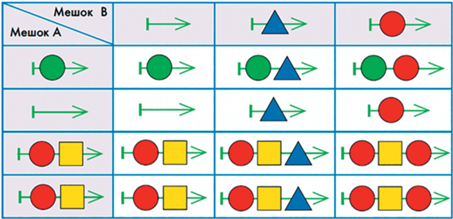
Для операции склеивания мешков удобно использовать таблицу, приведенную на рис. 58.

Рис. 58.

Использование двумерной таблицы для склеивания двух мешков цепочек.

14. ПРЕОБРАЗОВАНИЕ ОДНИХ СТРУКТУР В ДРУГИЕ

Таблица мешка. В таблице мешка указано, сколько каких объектов находится в мешке. Таблица может быть одномерной (мы уже упоминали такие таблицы при определении одинаковости мешков) или двумерной. Иногда мы добавляем к таблице:

● еще один столбец справа, в каждой клетке этого столбца мы суммируем числа из предшествующих клеток строки,

● еще одну строку снизу, в каждой клетке этой строки мы суммируем числа из стоящих выше клеток столбца.

В таблице возникает и угловая клетка, добавленная и в строке, и в столбце. В ней тоже получается сумма. При этом могли бы получиться и две суммы – из строки и из столбца. Но они – одинаковые! Замечательная исследовательская задача для каждого ученика – почему?

Мешок однозначно определен своей таблицей, если задана цепочка имен строк и столбцов. Мешки одинаковы тогда и только тогда, когда их таблицы заполняются одинаково (имеется в виду, что сами таблицы – одинаковые, то есть у них заданы одни и те же цепочки имен строк и имен столбцов).

Рис. 59.

Пример таблицы мешка с добавленными суммарными столбцом и строкой.

Интересные задачи получаются, если заполнены некоторые добавленные клетки и некоторые исходные (рис. 60).

Рис. 60.

Пример задачи о заполнении таблицы мешка с добавленными суммарными клетками.

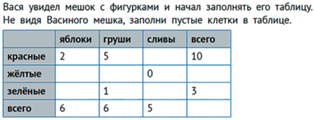
Ученики и сами могут придумывать задачи, в которых требуется заполнить таблицу (см., например, табл. 1), пользуясь разнообразной числовой информацией об объектах. Возможно, они встретятся с ситуациями, когда решений у задачи не будет, или, наоборот, будет несколько решений. И здесь начинается совсем серьезная математика.

На прилавке, в 10 рядов по 9 штук, выложена рождественская выпечка: разные пряники и 70 коржиков. Имбирных пряников только 10 осталось… Жалко! Зато есть медовые – и не только пряники, но и коржики. 60 штук. Сколько на прилавке медовых коржиков?

Работа с таблицами является первым шагом в понимании и применении динамических таблиц (spreadsheets).

Склеить цепочку в цикл можно только одним способом (см. рис. 61).

Рис. 61.

Склеивание цепочки в цикл.

Разрезать цикл, чтобы получить цепочку, можно по любой стрелке (см. рис. 62).

Рис. 62.

Задача о разрезании циклов.

Иногда восстановить цепочку по циклу, из которого она получилась разрезанием, оказывается непросто (см. рис. 63).

Рис. 63.

Задача о восстановлении цепочки по циклу.

Количество разных цепочек, которые получаются разрезанием данного цикла, не превосходит количество элементов цикла, но может быть и меньше, если у цикла есть симметрии.

Из цикла длины 7 разрезанием получается либо одна, либо 7 различных цепочек. Для любого делителя m длины цикла N можно придумать цикл длины N, разрезанием которого можно будет получить ровно m различных цепочек.

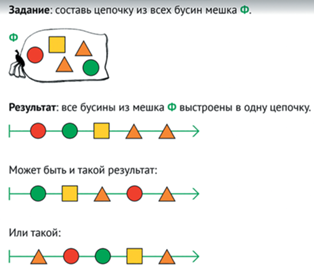
Мешок бусин цепочки, цикла. Из всех бусин мешка можно построить много разных цепочек (см. рис. 64).

Рис. 64.

Определение цепочки из всех бусин мешка.

А вот мешок бусин данной цепочки – только один.

Сколько разных циклов можно собрать из данного мешка бусин? Если все бусины одинаковые – то только один. А если среди них есть разные, а если есть одинаковые? Подробнее тема полного перебора вариантов обсуждается в статье этого сборника [М.А. Посицельская. Перебор, перечисление, поиск, построение в задачах для начальной школы].

15. ПРОЦЕССЫ

Процессы, идущие в наглядной среде, и задание этих процессов с помощью программ и правил игры, дают важные содержательные классы задач. Эти задачи очевидным образом содействуют достижению целей современного математического образования в начальной школе, формированию computational thinking (вычислительного, цифрового мышления) и подготовки к продолжению образования и жизни в цифровом мире. Об этом говорил А.П. Ершов своим лозунгом “Программирование – вторая грамотность” [6, 7].

Мы лишь бегло касаемся данного круга задач в данной статье, не приводим всех необходимых определений и отсылаем читателя к российским курсам информатики, в создании которых авторы принимали участие в последние десятилетия [9, 10, 30].

Исполнитель Водолей (реализован как stand-alone программа на компьютере) помогает учителям легко сформулировать задачи о переливании, а второклассникам – сделать много попыток решения, а получив ответ, иметь перед глазами путь, который привел к его получению – цепочку команд. Для решения такой задачи на бумаге необходимо заполнить таблицу состояний, что, конечно, занимает гораздо больше учебного времени, чем в экранной среде (см. рис. 65).

Рис. 65.

Задача в бумажном учебнике об исполнителе Водолей.

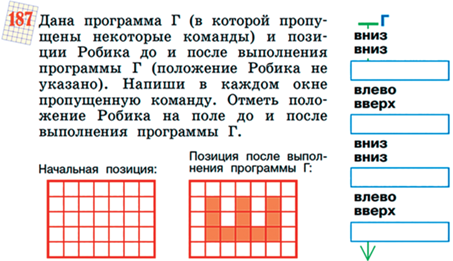
Задачи об исполнителе Робик являются пропедевтикой, подготовкой в работе с исполнителем Робот в средней школе. Робик работает на клетчатом поле, умеет выполнять четыре команды: вверх, вниз, вправо, влево и автоматически закрашивает клетку, через которую проходит. Помимо простых линейных программ, в курсе вводится конструкция повторения (цикл) (см. рис. 66).

Рис. 66.

Задача в бумажном учебнике об исполнителе Робик.

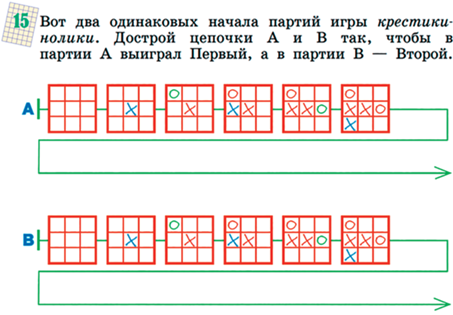
Игра с полной информацией – это игра, в которой после каждого хода всем игрокам известны все прошлые позиции игры и все позиции, которые могут получиться после очередного хода игрока. В курсе рассматривается несколько игр двух игроков с простыми правилами: камешки, крестики-нолики, ползунок, сим. Партия игры – цепочка позиций игры (см. рис. 67).

Рис. 67.

Задача о построении партий игры крестики-нолики с указанным победителем в каждой партии.

Для простых игр с небольшим количеством вариантов возможных позиций можно построить полное дерево игры. Это удобно для того, чтобы исследовать все позиции и построить выигрышную стратегию, если она есть. Например, на рис. 68 показано полное дерево игры камешки, в начальной позиции которой 7 камешков, разрешается брать 1, 3 или 4 камешка за ход. Для каждой позиции указано количество оставшихся камешков. Синим раскрашены проигрышные (с точки зрения игрока, чья очередь делать ход) позиции, красным – выигрышные (см. рис. 68).

Рис. 68.

Полное дерево игры в камешки, в начальной позиции которой имеется 7 камешков и в которой за ход разрешено брать 1, 3 или 4 камешка.

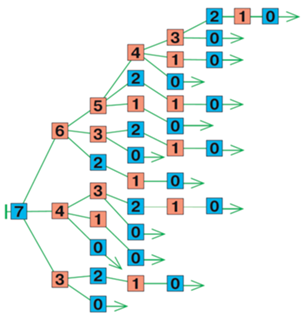
Заключительные позиции (листья дерева) – всегда проигрышные (игра закончилась, тот игрок, чья очередь ходить, уже проиграл). Затем, идя от листьев к началу дерева, раскрашиваем позицию красным, если среди следующих после нее позиций есть хотя бы одна, раскрашенная синим. В результате получили, что начальная позиция игры синяя – значит, Первый игрок не имеет выигрышной стратегии, а Второй может выиграть, если будет делать каждый раз такой ход, который оставляет противнику проигрышную позицию.

16. ЗАКЛЮЧЕНИЕ

Оглядываясь сегодня на 35-летний опыт создания учебных материалов, учебников, программ и стандартов, их использования сотнями учителей и десятками тысяч учащихся мы можем констатировать устойчивость предлагаемого подхода, доступность его для учителей, готовых заново посмотреть на школьную математику, работу учащегося и среду этой работы. Среди созданных нами курсы были и те, что успешно сочетали основной обсуждаемый выше материал с более традиционными темами школьной арифметики. Нам представляется, что и такое сочетание может быть продуктивным, эффективно помогать традиционному компоненту. Также кажется очевидной актуальность этой новой математической основы для computational thinking [31, 32] и mathematical digital competency [33].

Нам представляется, что наш подход свободен от очевидных недостатков New Math. Единственная существенная проблема с его дальнейшим распространением – это интеллектуальная инерция, естественное сопротивление всему новому, “непохожему”. Мы можем констатировать значительное сопротивление этому подходу со стороны большинства профессиональных математиков и лиц, принимающих решение в области подготовки учителей и экзаменационных материалов.

Завершая это обсуждение, остановимся еще раз на препятствиях, которые возникают на пути реализации нашего подхода как с точки зрения системы базовых объектов и типов заданий, так и с точки зрения методики. Мы обсуждали необходимость иметь задачи разной степени сложности, в частности, последовательности задач, где каждое приращение сложности будет оптимальным для каждого ученика. Тем самым, общее количество задач увеличивается по сравнению с вариантом для одного учащегося. Еще одна проблема связана со следующим. Традиционный арифметический пример или текстовая задача занимает в задачнике или учебнике немного места на странице. Наших же задач нам удается разместить на странице, обычно, не больше пяти, а иногда одна задача занимает больше страницы. Если учитывать оба обстоятельства – необходимость иметь больше задач и для каждой использовать больше места на странице, – то получается увеличение объема задачника в несколько раз по сравнению с традиционным. Естественно, это отражается на стоимости издания, особенно с учетом использования цветной печати. Тем не менее наши бумажные пособия используются в десятках государственных и частных школ. Но наш опыт показывает, что стоимость производства учебника оказывается существенным препятствием. Выход из этой ситуации сегодня очевиден: это учебник (задачник) на цифровом носителе – на экране планшета.

Мы продолжаем свою работу и считаем важным знакомить с ней учителей, родителей, математиков и широкое сообщество.