Доклады Российской академии наук. Математика, информатика, процессы управления, 2023, T. 514, № 2, стр. 212-224
ОПТИМАЛЬНЫЙ АНАЛИЗ МЕТОДА С БАТЧИРОВАНИЕМ ДЛЯ СТОХАСТИЧЕСКИХ ВАРИАЦИОННЫХ НЕРАВЕНСТВ ВИДА КОНЕЧНОЙ СУММЫ
А. Пичугин 1, М. Печин 1, А. Безносиков 1, *, А. Савченко 2, А. Гасников 1
1 Московский физико-технический институт
Долгопрудный, Россия
2 Лаборатория искусственного интеллекта, ПАО “Сбербанк”
Москва, Россия
* E-mail: beznosikov.an@phystech.edu
Поступила в редакцию 01.09.2023
После доработки 15.09.2023
Принята к публикации 18.10.2023
- EDN: BDNXBY
- DOI: 10.31857/S2686954323601598
Аннотация
Вариационные неравенства являются унифицированной оптимизационной постановкой, которая интересна не только сама по себе, но и потому что включает в себя задачи минимизации и поиска седловой точки. Между тем современные приложения побуждают рассматривать стохастические формулировки оптимизационных задач. В данной работе представлен анализ метода, имеющего оптимальные оценки сходимости для монотонных стохастических вариационных неравенств вида конечной суммы. В отличие от предыдущих работ, наш метод поддерживает батчирование и не теряет оптимальности оракульной сложности для любых размеров батча. Эффективность алгоритма, особенно в случае малых, но не единичных батчей, подтверждается численными экспериментами.
1. ВВЕДЕНИЕ
В данной работе рассматривается следующая задача вариационного неравенства:
(1)
$\begin{gathered} {\text{Найти}}\;x{\kern 1pt} * \in \mathcal{X}\;{\text{такие,}}\;{\text{что}}\;\langle F(x{\kern 1pt} *),x - x{\kern 1pt} *\rangle + \\ \, + g(x) - g(x{\kern 1pt} *) \geqslant 0,\quad \forall x \in \mathcal{X}, \\ \end{gathered} $Пример 1 (Минимизация). Рассмотрим выпуклую задачу минимизации с регуляризатором:
где f – целевая функция, а g – регуляризатор. Если взять $F(x): = \nabla f(x)$, то можно доказать, что $x{\kern 1pt} * \in {\text{dom}}g$ является решением (1) тогда и только тогда, когда $x{\kern 1pt} * \in {\text{dom}}g$ является решением (2) [1, Section 1.4.1].Пример 2 (Седловая задача). Рассмотрим выпукло-вогнутую седловую задачу:
(3)
$\mathop {\min }\limits_{{{x}_{1}} \in {{\mathbb{R}}^{{{{d}_{1}}}}}} \mathop {\max }\limits_{{{x}_{2}} \in {{\mathbb{R}}^{{{{d}_{2}}}}}} f({{x}_{1}},{{x}_{2}}) + {{g}_{1}}({{x}_{1}}) - {{g}_{2}}({{x}_{2}}),$В то время как задачи минимизации обычно рассматриваются отдельно от вариационных неравенств, задачи поиска седловых точек очень часто изучаются именно в общности вариационных неравенств. Но даже не принимая во внимание задачи минимизации сами вариационные неравенства [2] и их частный случай – седловые задачи – имеют множество приложений в реальных приложениях. Тут, прежде всего, следует отметить классические примеры из экономики и теории игр, расцвет которых пришелся на середину прошлого века [1, 3, 4]. Важно отметить также классические, но более новые сюжеты из области робастной оптимизации [5–7] и обучения с учителем/без учителя [8–13]. Еще большую значимость вариационным неравенствам придают новые приложения из областей обучения с подкреплением [14, 15], состязательного обучения [16] и генеративных моделей [17–20].
Между тем с каждым годом современные прикладные задачи становятся все более сложными и имеют стохастический характер: F(x) = ${{\mathbb{E}}_{{\xi \sim \mathcal{D}}}}[{{F}_{\xi }}(x)]$. Часто такое математическое ожидание не может быть представлено в аналитической форме из-за того, что распределение $\mathcal{D}$ является нетривиальным или даже неизвестным, поэтому прибегают к подходу Монте-Карло, который аппроксимирует интеграл с помощью выборки из распределения $\mathcal{D}$:
В алгоритмах, предназначенных для решения стохастических задач [21–24], часто избегают обращения к полным операторам или градиентам и прибегают к технике батчирования, когда выбирается одно или несколько слагаемых из (4). Поэтому очень важно, чтобы алгоритм был устойчив при использовании батчей любого размера, что подтверждается как с точки зрения теории, так и на практике. Но даже для задач минимизации не все стохастические методы обладают данным свойством [25, Раздел 5]. Это подводит нас к цели данной работы:
Разработать алгоритм решения монотонного стохастического вариационного неравенства вида конченой суммы с липшицевыми слагаемыми (1) + (4). При этом алгоритм должен быть нечувствителен к размеру батчей.
Краткий обзор существующих результатов. Теория решения монотонных вариационных неравенств с липшицевым оператором имеет обширную историю. Естественной идеей для создания методов для решения вариационных неравенств является обобщение градиентного спуска с помощью замены градиента $\nabla f(x)$ на оператор $F(x)$. Однако для монотонных операторов такой метод может расходиться. Прорывом стало создание экстраградиентного метода [26], который был широко теоретически исследован [7, 27] и впоследствии получил различные модификации и обобщения [28, 29], в том числе и для стохастического случая [30]. Что касается методов решения монотонных стохастических задач вида конечной суммы, то можно выделить работы [31–33], в которых авторы адаптируют технику редукции дисперсии для вариационных неравенств. Более того, результаты из [32] являются оптимальными [34]. Но это справедливо только для случая, когда на каждой итерации мы собираем батч размера один. Как только мы используем неединичный батч, результаты работ [31, 32] становятся хуже. Подробнее см. табл. 1.
Таблица 1.
Сравнение оракульных сложностей нахождения $\varepsilon $-решения монотонного стохастического вариационного неравенства вида конечной суммы с липшицевыми операторами (1) + (4). Сходимость измеряется с помощью зазора двойственности. Обозначения: $\mu $ = константа сильной монотонности оператора $F$, $L$ = константы Липшица для всех ${{F}_{i}}$, $n$ = размер локального датасета, $b$ = размер батча
| Источник | Сложность | Дополнительные предположения |
|---|---|---|
| Nemirovski et al. [7](1) | $\mathcal{O}\left( {n\frac{L}{\varepsilon }} \right)$ | |
| Carmon et al. [31] | $\tilde {\mathcal{O}}\left( {\sqrt {bn} \frac{L}{\varepsilon }} \right)$ | $x \to \langle F(x) + \nabla g(x),x - u\rangle $ выпуклая для любой u или ограниченной области |
| Alacaoglu and Malitsky [32] | $\mathcal{O}\left( {\sqrt {bn} \frac{L}{\varepsilon }} \right)$ | |
| Alacaoglu et al. [33] | $\mathcal{O}\left( {n\frac{L}{\varepsilon }} \right)$ | |
| This paper | $\mathcal{O}\left( {\sqrt n \frac{L}{\varepsilon }} \right)$ | |
| Han et al. [34] | $\Omega \left( {\sqrt n \frac{L}{\varepsilon }} \right)$ | нижняя оценка |
В данной статье предложено решение этой проблемы и представлен метод, оптимальный для любого размера батча. Идея основана на оптимистической схеме с моментумом из статьи [35]. Однако в указанной работе авторами были рассмотрены только сильно монотонные вариационные неравенства, тогда как в данной статье рассматриваеютя более общие и более сложные с точки зрения теоретического анализа монотонные вариационные неравенства.
2. ПОСТАНОВКА ЗАДАЧИ И ПРЕДПОЛОЖЕНИЯ
В работе рассматривается задача (1) + (4), где $\mathcal{X}$ – конечномерное евклидово пространство со скалярным произведением $\langle \cdot , \cdot \rangle $ и индуцированной нормой ${\text{||}}\, \cdot \,{\text{||}}$. Для выпуклой полунепрерывной g обозначим ее область определения как domg = = $\{ x:g(x) < + \infty \} $. Предполагаем, что функция $g$ является такой, что оператор prox(x) = = $\arg {{\min }_{{y \in \mathcal{X}}}}\left\{ {\alpha g(y) + \frac{1}{2}{\text{||}}y - x{\text{|}}{{{\text{|}}}^{2}}} \right\}$ при любом $\alpha > 0$ может быть точно вычислен “бесплатно”. Отметим важное свойство prox, а именно для y = ${\text{pro}}{{{\text{x}}}_{{\alpha g}}}(x)$ выполняется
Через ${{\mathbb{E}}_{k}}$ обозначим условное матожидание $\mathbb{E}\left[ { \cdot \,{\text{|}}\,{{S}^{{k - 1}}},{{S}^{{k - 2}}}, \cdot \cdot \cdot ,{{S}^{0}}} \right].$
Каждый оператор ${{F}_{i}}:{\text{dom}}g \to {{\mathbb{R}}^{d}}$ является однозначным. Основные предположения работы формулируются следующим образом.
Предположение 1.
$ \bullet $ Решение задачи (1) + (4) существует и может быть не единственным.
$ \bullet $ Оператор $F$ монотонный, т.е. для любых $u,v \in {{\mathbb{R}}^{d}}$ выполняется
$ \bullet $ Оператор $F$ $L$-липшицевый, т.е. для любых $u,v \in {{\mathbb{R}}^{d}}$ выполняется
$ \bullet $ Оператор ${{F}_{m}}$ является ${{L}_{m}}$-липшицевым. Определим $\bar {L}$, как ${{\bar {L}}^{2}} = \frac{1}{M}\sum\limits_{m = 1}^M {L_{m}^{2}} $.
3. ОСНОВНАЯ ЧАСТЬ
В основу описанного в данной статье метода положена нераспределенная версия Алгоритма 1 из статьи [35]. Данный алгоритм основан на так называемой “оптимистической” модификации [28] метода экстраградиента [26]. Суть этой модификации заключается в использовании значения оператора не только в точках текущей итерации (${{x}^{k}}$ и ${{w}^{k}}$), но и с прошлой итерации (${{x}^{{k - 1}}}$ и ${{w}^{{k - 1}}}$). Также в методе используется техника редукции дисперсии [22, 32], для чего введена дополнительную последовательность ${{w}^{k}}$. Отметим, что точка ${{w}^{k}}$ (опорная точка) меняется редко (если p мало), и поэтому полный оператор $F({{w}^{k}})$ практически не пересчитывается. Также в данной работе применен случайный отрицательный момент $\gamma ({{w}^{k}} - {{x}^{k}})$, который необходим для применения техники редукции дисперсии в методах вариационных неравенств [32, 33].
В качестве критерия сходимости используем следующую функцию:
(6)
${\text{Gap}}(z) = \mathop {\sup }\limits_{u \in \mathcal{C}} \left[ {\langle F(u),z - u\rangle + g(x) - g(u)} \right].$Здесь мы берем максимум не на всем множестве $\mathcal{X}$, а на $\mathcal{C}$ – компактном подмножестве $\mathcal{X}$. Таким образом, мы можем рассматривать и неограниченные множества $\mathcal{X} \subseteq {{\mathbb{R}}^{d}}$. Это допустимо, поскольку рассмотренная версия критерия справедлива, если решение $x{\kern 1pt} *$ лежит в $\mathcal{C}$; подробнее см. [6]. Следующая теорема представляет сходимость предложенного метода.
Теорема 1. Рассмотрим задачу (1) + (4) в Предположениях 1. Пусть $\{ {{x}^{k}}\} $ – последовательность, генерируемая Алгоритмом 3 с выбранными $\eta ,\theta ,\alpha ,\beta ,\gamma $ следующим образом:
Тогда, при $\varepsilon > 0$, количество итераций для достижения $\mathbb{E}[{\text{Gap}}({{x}^{k}})]\;\leqslant \;\varepsilon $ равно
Algorithm 1. Оптимистичный Метод с Моментум и Батчированием
1: Параметры: размер шага $\eta > 0$, момент $\gamma > 0$, вероятность $p \in (0;1)$, размер батча $b \in \{ 1, \ldots ,M\} $, количество итераций K
2: Инициализация: выбрать ${{x}^{0}} = {{w}^{0}} = {{x}^{{ - 1}}} = {{w}^{{ - 1}}} \in {{\mathbb{R}}^{d}}$
3: for $k = 0,1, \ldots ,$ do
4: Выбрать $j_{1}^{k}, \ldots ,j_{b}^{k}$ случайным образом из $\{ 1,...,M\} $ независимо и равномерно
5: ${{S}^{k}} = \{ j_{1}^{k},...,j_{b}^{k}\} $
6: ${{\Delta }^{k}} = \frac{1}{b}\sum\limits_{j \in {{S}^{k}}}^{} {({{F}_{j}}({{x}^{k}}) - {{F}_{j}}({{w}^{{k - 1}}})} + ({{F}_{j}}({{x}^{k}}) - {{F}_{j}}({{x}^{{k - 1}}}))) + F({{w}^{{k - 1}}})$
7: ${{x}^{{k + 1}}} = {\text{pro}}{{{\text{x}}}_{{\eta g}}}({{x}^{k}} + \gamma ({{w}^{k}} - {{x}^{k}}) - \eta {{\Delta }^{k}})$
8: ${{w}^{{k + 1}}} = \left\{ \begin{gathered} {{x}^{{k + 1}}},\quad {\text{с}}\;{\text{вероятностью}}\;p \hfill \\ {{w}^{k}},\quad {\text{с}}\;{\text{вероятностью}}\;1 - p \hfill \\ \end{gathered} \right.$
9: end for
Доказательство см. в Приложении A . Отметим, что Теорема дает итерационную сложность Алгоритма 3, но интерес представляет, прежде всего, оракульная сложность (количество обращений к слагаемым ${{F}_{i}}$). Можно заметить, что на каждой итерации в среднем вызывается $\mathcal{O}\left( {b + pn} \right)$ слагаемых – каждый раз вызывается батч размера $b$, и с вероятностью $p$ вычисляется полный оператор. Отсюда сразу получаем оптимальный выбор для $p$:
Следствие 1. В условиях теоремы 1 при выборе $p = \frac{b}{n}$ получается следующая оракульная сложность для Алгоритма 1
Если $b\;\leqslant \;\frac{{\overline L \sqrt n }}{L}$, то получаем $\mathcal{O}\left( {\sqrt n \frac{{\bar {L}}}{\varepsilon }} \right)$. Этот результат является оптимальным и неулучшаемым [34].
4. ЭКСПЕРИМЕНТЫ
В данном разделе проверяется эффективность работы алгоритма 1 на практике.
Рассмотрим билинейную задачу:
(7)
$\mathop {\min }\limits_{x \in {{\Delta }^{d}}} \mathop {\max }\limits_{y \in {{\Delta }^{d}}} {{x}^{ \top }}Ay,$Для сравнения взяты методы из табл. 1. В частности, выбраны Алгоритмы 1 и 2 из [32], Алгоритм 1 + 2 из [31]. Все алгоритмы рассматриваются в евклидовой постановке с проекцией на симплекс из [38].
Параметры всех методов настраиваются, исходя из теоретических результатов, соответствующих статей – см. Раздел 6 из [32]. Все методы проверяются с различными размерами батчей. В качестве критерия сходимости используется зазор двойственности (6), который вычисляется как $\left[ {{{{\max }}_{i}}{{{({{A}^{T}}x)}}_{i}} - {{{\min }}_{j}}{{{(Ay)}}_{j}}} \right]$ ввиду решения задачи на симплексе. Критерием сравнения является количество операций (одна операция вычислительно равна вычислениям Ay и ${{A}^{T}}x$).
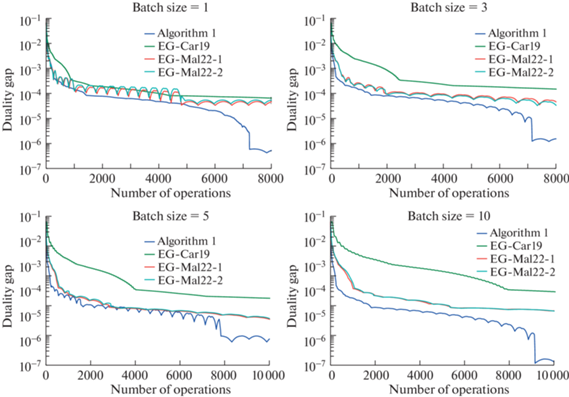
Результаты отражены на рис. 1 и 2. Они показывают, что алгоритм 3 превосходит всех конкурентов.
Рис. 1.
Сравнение вычислительных сложностей для Алгоритма 3, EG-Mal22-1 (Алгоритм 1 [32]), EG-Mal22-2 (Алгоритм 2 [32]), EG-Car19 (Алгоритм 1+2 из [31]) на (7) с матрицей полицейского и грабителя из [36].
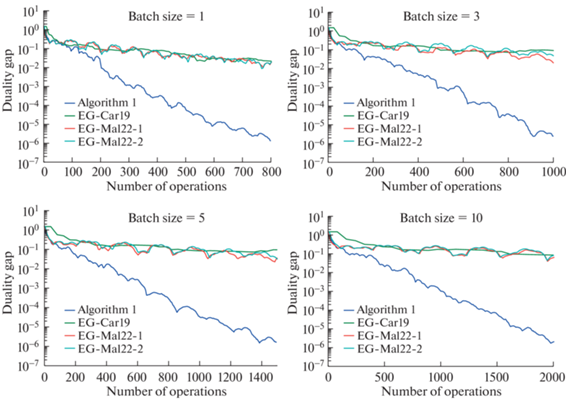
Рис. 2.
Сравнение вычислительных сложностей для алгоритма 3, EG-Mal22-1 (Алгоритм 1 [32]), EG-Mal22-2 (Алгоритм 2 [32]), EG-Car19 (Алгоритм 1+2 из [31]) на (7) с первой тестовой матрицей из [37].
5. ВЫВОДЫ
В статье представлен алгоритм решения монотонных стохастических вариационных неравенств вида конечной суммы с липшицевыми слагаемыми. С теоретической точки зрения алгоритм является оптимальным практически для любого размера батча. В качестве направлений дальнейшей работы авторов интересует получение версии Алгоритма 3 в неевклидовом случае с произвольной дивергенцией Брэгмана.
Список литературы
Facchinei F., Pang J.-S. Finite-Dimensional Variational Inequalities and Complementarity Problems (Springer Series in Operations Research). Springer, 2003.
Scutari G., Palomar D.P., Facchinei F., Pang J.-S. “Convex optimization, game theory, and variational inequality theory,” IEEE Signal Processing Magazine. 2010. V. 27. № 3. P. 35–49.
Neumann J.V., Morgenstern O. Theory of games and economic behavior. Princeton University Press, 1944.
Harker P.T., Pang J.-S. “Finite-dimensional variational inequality and nonlinear complementarity problems: A survey of theory, algorithms and applications,” Mathematical programming, 1990.
Ben-Tal A., Ghaoui L.E., Nemirovski A. Robust Optimization. Princeton University Press, 2009.
Nesterov Y. “Dual extrapolation and its applications to solving variational inequalities and related problems,” Mathematical Programming. 2007. V. 109. № 2. P. 319–344.
Nemirovski A. “Prox-method with rate of convergence o (1/t) for variational inequalities with lipschitz continuous monotone operators and smooth convex-concave saddle point problems,” SIAM Journal on Optimization. 2004. V. 15. № 1. P. 229–251.
Joachims T. “A support vector method for multivariate performance measures,” Jan. 2005. P. 377–384. https://doi.org/10.1145/1102351.1102399
Bach F., Jenatton R., Mairal J., Obozinski G. “Optimization with sparsity-inducing penalties,” arXiv preprint arXiv:1108.0775, 2011.
Xu L., Neufeld J., Larson B., Schuurmans D. “Maximum margin clustering,” in Advances in Neural Information Processing Systems. 2005. V. 17. P. 1537–1544.
Bach F., Mairal J., Ponce J. “Convex sparse matrix factorizations,” arXiv preprint arXiv:0812.1869, 2008.
Esser E., Zhang X., Chan T.F. “A general framework for a class of first order primal-dual algorithms for convex optimization in imaging science,” SIAM Journal on Imaging Sciences. 2010. V. 3. № 4. P. 1015–1046.
Chambolle A., Pock T. “A first-order primal-dual algorithm for convex problems with applications to imaging,” Journal of mathematical imaging and vision. 2011. V. 40. № 1. P. 120–145.
Omidshafiei S., Pazis J., Amato C., How J.P., Vian J. “Deep decentralized multi-task multi-agent reinforcement learning under partial observability,” in Proceedings of the 34th International Conference on Machine Learning (ICML). V. 70, PMLR, 2017. P. 2681–2690. [Online]. Available: http://proceedings.mlr.press/v70/omidshafiei17a.html.
Jin Y., Sidford A. “Efficiently solving MDPs with stochastic mirror descent,” in Proceedings of the 37th International Conference on Machine Learning (ICML). V. 119, PMLR, 2020. P. 4890–4900.
Madry A., Makelov A., Schmidt L., Tsipras D., Vladu A. “Towards deep learning models resistant to adversarial attacks,” in International Conference on Learning Representations (ICLR), 2018.
Goodfellow I.J., Pouget-Abadie J., Mirza M. et al., Generative adversarial networks, 2014. arXiv: 1406.2661 [stat.ML].
Daskalakis C., Ilyas A., Syrgkanis V., Zeng H. “Training gans with optimism,” arXiv preprint arXiv:1711.00141, 2017.
Gidel G., Berard H., Vignoud G., Vincent P., Lacoste-Julien S. “A variational inequality perspective on generative adversarial networks,” arXiv preprint arXiv:1802.10551, 2018.
Mertikopoulos P., Lecouat B., Zenati H., Foo C.-S., Chandrasekhar V., Piliouras G. “Optimistic mirror descent in saddle-point problems: Going the extra (gradient) mile,” arXiv preprint arXiv:1807.02629, 2018.
Robbins H., Monro S. “A Stochastic Approximation Method,” The Annals of Mathematical Statistics. 1951. V. 22. № 3. P. 400–407.
Johnson R., Zhang T. “Accelerating stochastic gradient descent using predictive variance reduction,” vol. 26, 2013. P. 315–323.
Defazio A., Bach F., Lacoste-Julien S. “Saga: A fast incremental gradient method with support for non-strongly convex composite objectives,” in Advances in neural information processing systems, 2014. P. 1646–1654.
Nguyen L.M., Liu J., Scheinberg K., Takáč M. “SARAH: a novel method for machine learning problems using stochastic recursive gradient,” in International Conference on Machine Learning, PMLR, 2017. P. 2613–2621.
Allen-Zhu Z. “Katyusha: The first direct acceleration of stochastic gradient methods,” in Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing, 2017. P. 1200–1205.
Korpelevich G.M. “The extragradient method for finding saddle points and other problems,” Matecon. V. 12. P. 35–49, 1977; Russian original: Economika Mat. Metody. 1976. V. 12. № 4. P. 747–756.
Mokhtari A., Ozdaglar A., Pattathil S. “A unified analysis of extra-gradient and optimistic gradient methods for saddle point problems: Proximal point approach,” in International Conference on Artificial Intelligence and Statistics, PMLR, 2020. P. 1497–1507.
Popov L.D. “A modification of the arrow-hurwicz method for search of saddle points,” Mathematical notes of the Academy of Sciences of the USSR. 1980. V. 28. P. 845–848.
Tseng P. “A modified forward-backward splitting method for maximal monotone mappings,” SIAM Journal on Control and Optimization. 2000. V. 38. № 2. P. 431–446.
Juditsky A., Nemirovski A., Tauvel C. “Solving variational inequalities with stochastic mirror-prox algorithm,” Stochastic Systems. 2011. V. 1. № 1. P. 17–58.
Carmon Y., Jin Y., Sidford A., Tian K. “Variance reduction for matrix games,” arXiv preprint arXiv:1907.02056, 2019.
Alacaoglu A., Malitsky Y. “Stochastic variance reduction for variational inequality methods,” arXiv preprint arXiv:2102.08352, 2021.
Alacaoglu A., Malitsky Y., Cevher V. “Forward-reflected-backward method with variance reduction,” Computational Optimization and Applications. V. 80, Nov. 2021. https://doi.org/10.1007/s10589-021-00305-3
Han Y., Xie G., Zhang Z. “Lower complexity bounds of finite-sum optimization problems: The results and construction,” arXiv preprint arXiv:2103.08280, 2021.
Kovalev D., Beznosikov A., Sadiev A., Persiianov M., Richt’arik P., Gasnikov A. “Optimal algorithms for decentralized stochastic variational inequalities,” arXiv preprint arXiv:2202.02771, 2022.
Nemirovski A. Mini-course on convex programming algorithms, 2013.
Nemirovski A., Juditsky A., Lan G., Shapiro A. “Robust stochastic approximation approach to stochastic programming,” SIAM Journal on optimization. 2009. V. 19. № 4. P. 1574–1609.
Condat L. “Fast projection onto the simplex and the l 1 ball,” Mathematical Programming. 2016. V. 158. № 1–2. P. 575–585.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления


