Доклады Российской академии наук. Науки о Земле, 2020, T. 490, № 2, стр. 51-56

ВВЕДЕНИЕ

Обеспокоенность неблагоприятными изменениями состава глобальной атмосферы и качества воздуха в городах способствовала развитию системы мониторинга атмосферы и методов численного моделирования атмосферных процессов. Существующие модели в целом адекватно описывают процессы переноса и химической трансформации газовых и аэрозольных примесей в атмосфере. Однако при рассмотрении многих сценариев отмечаются значительные расхождения между результатами расчетов и данными наблюдений. Выделяются две основные причины таких расхождений – это значительная доля субъективизма в задании эмиссий газовых и аэрозольных примесей антропогенного происхождения [1, 2] и большие неопределенности в описании турбулентной диффузии в атмосферном пограничном слое (АПС) [3, 4].

В работах [2, 5] были предложены методы определения антропогенных эмиссий газов и аэрозолей по данным измерений вертикальной стратификации ветра, температуры и концентрации примесей в АПС над городом. Полученные для Москвы и других крупных городов России значения эмиссий [2, 5] оказались существенно точнее, чем те, которые содержатся в широко используемых глобальных базах данных EDGAR, RETRO, IPCC-AR4 и др. [1, 6], собранных в основном по косвенным сведениям о мощности около 40 видов источников (автотранспорт, химическая промышленность и др.). Это показывают результаты использования новых эмиссий в численных моделях [7] и приближение последних версий инвентаризаций (например, EDGAR v 4.3 (2019)) к значениям эмиссий, полученным в [2, 5].

Наибольшую погрешность вычисления эмиссий по данным прямых измерений дают неопределенности, связанные с отсутствием достоверной информации о вертикальном профиле коэффициента турбулентной диффузии $k(z,t)$ в нейтральном и устойчивом АПС. Существует несколько вариантов определения и параметризации $k(z,t)$. Почти все они основаны на теории подобия Монина–Обухова [8]. Но, как показали результаты численного моделирования, эти схемы расчета $k(z,t)$ часто не применимы для устойчивого АПС, характерного для ночного времени и слабых ветров [9, 10]. В настоящее время большое распространение получил метод определения $k(z,t)$ в нейтральном и устойчивом АПС Grisogono [10] и его модификации [4, 11], основанные на вычислении эмпирических коэффициентов по данным о вертикальной стратификации ветра и температуры с высоким (10–20 м) разрешением по высоте (LES-данные). Однако и эти процедуры не всегда адекватно отражают реальные условия, свойственные крупным городам [4]. К тому же столь подробные метеорологические наблюдения проводятся лишь в ходе специально поставленных экспериментов, результаты которых отражают в основном состояние атмосферного пограничного слоя в данном месте в данное время.

В настоящей работе обосновывается новый подход к восстановлению вертикального профиля $k(z,t)$ по данным измерений концентрации примесей на 2–4-х высотных уровнях в устойчивом или нейтральном пограничном слое. Такие измерения несложно проводить во всех городах, а также в сельской местности при размещении сенсоров на ретрансляционных вышках. Результаты наблюдений скорости накопления примесей в приземном воздухе и рассчитанные значения $k(z,t)$ являются основой для определения антропогенных и природных эмиссий химически активных веществ и прогнозирования возможных изменений состава атмосферы [2, 5].

ПОСТАНОВКА ЗАДАЧИ. АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ

Изменение вертикального распределения концентрации антропогенной примеси, обусловленное диффузионным процессом, описывается задачей

где $c(z,t)$ – концентрация вещества, $k(z,t) > 0$ – коэффициент турбулентной диффузии, ${{c}^{0}}(z)$ – распределение концентрации в момент времени $t = 0$, ${{c}_{1}}(t)$ – распределение концентрации на высоте $z = {{z}_{0}}$, $H(t)$ – ширина АПС.

Зависимостью коэффициента $k(z,t)$ от времени на интервале $T$ в несколько часов можно пренебречь, а в качестве границы $z = H(t)$ выбрать среднее значение $\bar {H}$ функции $H(t)$ на указанном интервале. С учетом этого в безразмерных переменных имеем сингулярно возмущенную модельную задачу

где функция ${{\varepsilon }^{2}}A(\bar {z}): = k(L\bar {z}){{\left( {L{{V}_{х}}} \right)}^{{ - 1}}}$ ~ ${{({{\Pr }_{D}}\operatorname{Re} )}^{{ - 1}}}$ $ \ll $ 1 для приземного слоя атмосферы, $\varepsilon > 0$ – малый параметр, $B(\bar {z})$ := ${{\partial A(\bar {z})} \mathord{\left/ {\vphantom {{\partial A(\bar {z})} {\partial{ \bar {z}}}}} \right. \kern-0em} {\partial{ \bar {z}}}}$, ${{u}^{0}}(\bar {z})$ := ${{c}^{0}}(L\bar {z}){{U}^{{ - 1}}}$, ${{u}_{1}}(\bar {t})$ := ${{c}_{1}}({{T}_{x}}\bar {t}){{U}^{{ - 1}}}$, ${{Z}_{0}}: = {{z}_{0}}{{L}^{{ - 1}}}$, ${{T}_{0}}: = T{{T}_{х}}^{{ - 1}}$, H₀ := := $\bar {H}{{L}^{{ - 1}}}$, V_x – характерная скорость, $L$ и ${{T}_{х}}$ – характерный пространственный и временной масштаб.

Асимптотическое решение задачи (1), (2) получается с использованием алгоритма А.Б. Васильевой [12]:

где ${{\bar {u}}_{0}}(\bar {z},\bar {t}) + \varepsilon {{\bar {u}}_{1}}(\bar {z},\bar {t}) + ...$ – регулярный ряд, ${{\Pi }_{0}}u(\rho ,\bar {t})$ + $\varepsilon {{\Pi }_{1}}u(\rho ,\bar {t}) + ...$ – пограничный ряд, описывающий пограничный слой с локализацией в окрестности точки $\bar {z} = {{Z}_{0}}$; ${{R}_{0}}u(\tau ,\bar {t})$ + + $\varepsilon {{R}_{1}}u(\tau ,\bar {t}) + ...$ – пограничный ряд, описывающий пограничный слой, локализованный в окрестности точки $\bar {z} = {{H}_{0}}$, $\rho = (\bar {z} - {{Z}_{0}}){{\varepsilon }^{{ - 1}}}$, $\tau = (\bar {z} - {{H}_{0}}){{\varepsilon }^{{ - 1}}}$.

Подставляя ряд (3) в задачу (1)–(2), приходим к последовательности задач для определения коэффициентов разложения (3). В частности, в нулевом приближении имеем: $\left( {{{\partial {{{\bar {u}}}_{0}}} \mathord{\left/ {\vphantom {{\partial {{{\bar {u}}}_{0}}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right) = 0$. Положим: ${{\bar {u}}_{0}}(\bar {z},t)$ = ${{u}^{0}}(\bar {z})$. В следующем приближении для коэффициента регулярного ряда получаем уравнение $\left( {{{\partial {{{\bar {u}}}_{1}}} \mathord{\left/ {\vphantom {{\partial {{{\bar {u}}}_{1}}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right) = 0$ с решением ${{\bar {u}}_{1}}(\bar {z},\bar {t}) = 0$, которое удовлетворяет условию ${{\bar {u}}_{1}}(\bar {z},0) = 0$. Далее, относительно функции ${{\bar {u}}_{2}}(\bar {z},\bar {t})$ приходим к уравнению

с решением ${{\bar {u}}_{2}}(\bar {z},\bar {t}) = \left( {A(\bar {z})\frac{{{{\partial }^{2}}{{u}^{0}}}}{{\partial {{{\bar {z}}}^{2}}}} + B(\bar {z})\frac{{\partial {{u}^{0}}}}{{\partial{ \bar {z}}}}} \right)\bar {t}$, удовлетворяющим условию ${{\bar {u}}_{2}}(\bar {z},0) = 0$ и возрастающим с ростом $\bar {t}$, что объясняется упрощенным описанием, не учитывающим наличие стоков вещества.

Относительно функций ${{\Pi }_{k}}u(\rho ,\bar {t})$ и ${{R}_{k}}u(\tau ,\bar {t})$ получаем, соответственно, начально-краевые задачи Дирихле и Неймана для линейного уравнения теплопроводности на полупрямой с решениями в явном виде. Например, при $k = 0$ или $k = 1$ имеем

Используя явный вид функций ${{\Pi }_{к}}u(\rho ,\bar {t})$ и ${{R}_{k}}u(\tau ,\bar {t})$, несложно доказать их экспоненциальное убывание с изменением аргументов $\rho $ и $\tau $:

где ${{C}_{k}}(\bar {t})$, ${{\nu }_{k}}(\bar {t})$, ${{\mu }_{k}}(\bar {t})$ – некоторые положительные функции, $k \geqslant 0$.

Доказательство существования классического решения задачи (1), (2) с асимптотикой (3) и оценка остаточного члена основаны на использовании принципа сравнения [13].

Функции ${{\alpha }^{{( \pm )}}}(\bar {z},\bar {t},\varepsilon )$ ∈ ${{C}^{2}}({{Z}_{0}},{{H}_{0}})$ × C¹(0, ${{T}_{0}}] \cap {{C}^{1}}[{{Z}_{0}},{{H}_{0}}]$ × $C[0,{{T}_{0}}]$ называются, соответственно, верхним и нижним решениями задачи (1), (2), если:

В соответствии с асимптотическим методом дифференциальных неравенств [12]:

где причем $0 < \Psi (\rho ,\bar {t}) < C(\bar {t}){{e}^{{ - \kappa (\bar {t})\rho }}}$, $C(\bar {t}) > 0$, $\kappa (\bar {t}) > 0$, $\bar {t} \in [0,{{T}_{0}}]$. Функция $\Delta (\bar {t})$ удовлетворяет условиям: $\Delta (\bar {t}) - \gamma > 0$, $\bar {t} \in (0,{{T}_{0}}]$, $\Delta (0) - \gamma = 0.$ Соответствующий выбор параметров $C(\bar {t})$, $\kappa (\bar {t})$, γ и $\Delta (\bar {t})$ обеспечивает выполнение неравенств (4), в чем легко убедиться, подставив функции (5) в неравенства (4).

Теорема. Пусть функции $A(\bar {z})$, $B(\bar {z})$, ${{u}^{0}}(\bar {z})$ дважды непрерывно дифференцируемы при $\bar {z} \in [{{Z}_{0}},{{H}_{0}}]$, функция ${{u}_{1}}(\bar {t})$ непрерывна при $\bar {t} \in [0,{{T}_{0}}]$, причем условия (2) согласованы. Тогда существует единственное классическое решение $u(\bar {z},\bar {t})$ задачи (1), (2) такое, что

где $C > 0$ не зависит от $\varepsilon $,

При переходе к размерным переменным в формуле (6) приходим к распределению концентрации:

Решение $u(\bar {z},\bar {t})$ задачи (1), (2) с асимптотикой (3) устойчиво по отношению к малым возмущениям начального распределения ${{u}^{0}}(\bar {z})$ в равномерной норме. Это свойство $u(\bar {z},\bar {t})$ следует из способа доказательства теоремы и существенно, поскольку распределение ${{u}^{0}}(\bar {z})$ дается с определенной погрешностью.

ВОССТАНОВЛЕНИЕ КОЭФФИЦИЕНТА ТУРБУЛЕНТНОЙ ДИФФУЗИИ

Для восстановления коэффициента турбулентной диффузии $k(z,t)$ в устойчивом и нейтральном пограничном слое атмосферы использовались данные измерений концентрации оксида углерода CO с 1 февраля по 31 декабря 2009 г. в утренние часы (с 7 : 00 до 10 : 00 местного времени) на высотных уровнях 10, 130, 248 и 348 м на телевизионной башне в Останкино. В это время суток происходит постепенный подъем и накопление СО в приземном воздухе по мере роста интенсивности дорожного движения и начала работы промышленных предприятий. Действующие на башне измерительные приборы, средства калибровки и методики измерений соответствовали требованиям Глобальной системы мониторинга Всемирной метеорологической организации (GAO WMO). Их подробное описание приведено в [5]. Для оценки качества данных применялись рекомендованные GAW WMO процедуры. На каждом высотном уровне по данным измерений рассчитывались среднемесячные значения концентрации СО. Эпизодические выбросы значений концентраций, связанные со скачками напряжения в электросети и выходящие за пределы ±3σ², исключались. Общее количество данных, по которым рассчитывались среднемесячные значения, менялось от 30 в июне до 102 в марте. В апреле из-за сильных ветров и большого числа облачных дней устойчивая стратификация наблюдалась редко, и результаты расчетов получились незначимыми. Далее, по формуле (7) вычислялось вертикальное распределение концентрации СО для каждого дня, при этом координата $z$ изменялась от 10 м до 348 м, а время $t$ – от 7 : 00 до 10 : 00. С целью получения начального распределения ${{c}^{0}}(z)$ использовались данные измерений на 4 высотах в 7 : 00, а в целях получения граничного условия ${{c}_{1}}(t)$ – данные измерений на высоте 10 м. Для того, чтобы обеспечить необходимую гладкость распределений ${{c}^{0}}(z)$ и ${{c}_{1}}(t)$, натурные измерения аппроксимировались базисными сплайнами [14] с учетом условия согласования начального и граничных условий задачи. Затем с использованием диффузионной модели вычислялись среднемесячные модельные значения концентрации СО на каждом уровне. Коэффициенты турбулентной диффузии рассчитывались с использованием линейно-экспоненциальной параметризации его вертикального профиля [10, 11]:

где ${{k}_{{\max }}}$ – максимальное значение коэффициента турбулентной диффузии, ${{z}_{{\max }}}$ – высота, которой он соответствует. Такая параметризация предполагает выполнение условия достижения максимального значения $k(z)$ на 1/3 высоты атмосферного пограничного слоя ${\bar {H}}$ над городом при устойчивой и нейтральной стратификации. Это условие выполняется и для других параметризаций, в частности параметризации О’Брайена [15]. С целью согласования модельных и натурных данных (в среднеквадратичном смысле) для каждого месяца численно подбирались параметры ${{k}_{{\max }}}$ и ${{z}_{{\max }}}$, присутствующие в формуле для расчета $k(z)$ [15].

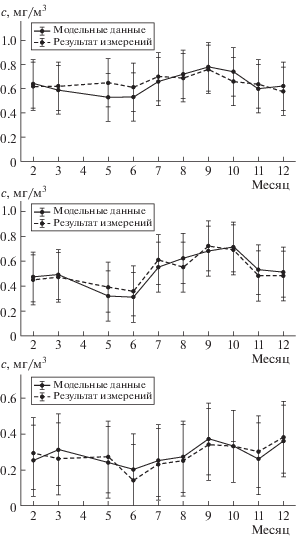
Среднемесячные значения концентрации СО представлены на рис. 1, где пунктирная линия соответствует результатам измерений, а сплошная – модельным данным. Повышенные концентрации на всех уровнях отмечаются в июле–октябре. Максимальная в этот период активность автотранспорта и наиболее высокое положение верхней границы АПС (260–350 м) способствуют хорошему перемешиванию [5]. Дополнительный вклад в увеличение СО на высоте 248 м вносят выбросы из высоких труб 22 крупных московских ТЭЦ. На уровне 348 м влияние вертикального перемешивания ослабевает, но повышается роль адвективного переноса от удаленных источников, расположенных за пределами мегаполиса. Влияние дальнего переноса сглаживает сезонные вариации СО.

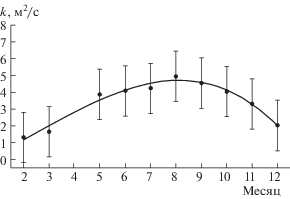
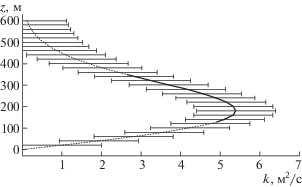
Сезонный ход $k(z)$ (пример приведен на рис. 2) в среднем повторяет сезонные вариации концентрации, что говорит о тесной связи между этими величинами. Повышенная интенсивность вертикального перемешивания в АПС над городом в июле–октябре вызвана прогревом земной поверхности и приземного воздуха, а также значительными антропогенными потоками тепла, в том числе связанных с началом отопительного периода в октябре. Пример восстановленного вертикального профиля $k(z)$ в августе 2009 г. представлен на рис. 3. Выделенный сплошной линией участок профиля показывает изменение коэффициента на высотах от 130 м до 350 м. В этом месяце турбулентное перемешивание является наиболее активным. Значение ${{k}_{{\max }}}$, равное 5.4 м²/c, отмечается на высоте 180 м, что подразумевает положение верхней границы АПС на высоте около 500 м. Наиболее слабое перемешивание – в феврале: ${{k}_{{\max }}} = 2.4$ м²/c, а соответствующая ему высота ${{z}_{{\max }}} = 70$ м.

ЗАКЛЮЧЕНИЕ

Рассчитанные для Москвы профили $k(z,t)$ и их сезонная изменчивость примерно повторяют характерные особенности турбулентной диффузии, полученные в результате исследований тонкой структуры вертикальной стратификации АПС над городами с похожей инфраструктурой и близкими климатическими условиями [4, 11], т.е. предложенный метод определения $k(z,t)$, основанный на использовании аналитического решения модельной задачи в сочетании с данными измерений, может широко применяться на сети станций мониторинга атмосферы, которые, как правило, не обеспечены средствами наблюдения вертикальной стратификации АПС с высоким разрешением. При этом есть возможность повысить надежность метода, если использовать данные измерений короткоживущих примесей, для которых дальний перенос не будет играть заметной роли. Таким образом, предложенный метод расчета $k(z,t)$ открывает большие перспективы перед определением эмиссий парниковых газов и химически активных соединений, необходимых для оценки и прогнозирования качества воздуха и состояния климатической системы.