Доклады Российской академии наук. Науки о Земле, 2021, T. 497, № 2, стр. 161-164

ВВЕДЕНИЕ

Моделирование волновых процессов в пористых средах представляет интерес не только в области разработки новых математических моделей, но и их практического применения в прикладных геофизических задачах. Это направление исследований становится особенно актуальным в связи с развитием цифровых технологий двойников геологических объектов.

История моделирования пористых сред берет начало с работ Био [1, 2], в которых впервые были сформулированы уравнения для описания распространения волн малой амплитуды в насыщенных упругих пористых средах и заложены основы для многочисленных обобщений модели Био (см. [3, 4] и ссылки в них).

В последнее десятилетие стал развиваться альтернативный подход, основанный на использовании континуальной теории многофазных сред (см. [5] и ссылки в ней). В сочетании с теорией термодинамически согласованных систем законов сохранения этот подход позволяет вывести математически корректную модель течения многофазной сжимаемой смеси в упруго деформируемом скелете, удовлетворяющую законам неравновесной термодинамики [6–8], и для случая малых деформаций дает качественно те же результаты, что и модель Био.

В работе используется термодинамически согласованная модель [8] в сочетании с методом диффузных границ для описания волн малой амплитуды в насыщенных образцах неоднородной пористой среды, в которых четко прослеживаются границы различной пористости, в том числе границы между чистой жидкостью и чисто упругим скелетом. Преимущество этого подхода заключается в использовании единой системы уравнений, в которой границы раздела задаются скачком объемной концентрации фаз.

УРАВНЕНИЯ

В этом разделе приводится система уравнений, описывающая распространение волн малой амплитуды в насыщенной упругой пористой среде в предположении, что в начальный момент времени среда неподвижна и напряжения в ней отсутствуют [8]. Уравнения образуют гиперболическую систему первого порядка и имеют вид:

Здесь ${{v}^{i}}$ – скорость смеси (жидкой и упругой фаз), ${{w}^{i}}$ – относительная скорость, $P$ – давление, ${{s}_{{ik}}}$ – девиатор напряжений в смеси фаз, $F$ – источник. Параметры среды определяются константами $\alpha _{1}^{0}$, $\rho _{1}^{0}$ – объемная доля и плотность жидкой фазы, $\alpha _{2}^{0}$, $\rho _{2}^{0}$ – объемная доля и плотность упругой фазы, $\mu $ – модуль сдвига Ламе, $K$ – объемный модуль, $\tau $ – время релаксации напряжений. Коэффициент межфазного трения $X$ вычисляется через плотность смеси $\rho = \alpha _{1}^{0}\rho _{1}^{0}$ + $\alpha _{2}^{0}\rho _{2}^{0}$ и массовые доли фаз $с_{1}^{0}$ = $\alpha _{1}^{0}\rho _{1}^{0}{\text{/}}\rho $, $с_{2}^{0}$ = $\alpha _{2}^{0}\rho _{2}^{0}{\text{/}}\rho $ по формуле $X = с_{1}^{0}с_{2}^{0}{\text{/}}\theta $, где $\theta $ – время релаксации к нулю относительной скорости. Пористость вычисляется как $\phi = \alpha _{1}^{0}$ = $1 - \alpha _{2}^{0}$.

Система (1) позволяет моделировать волновые поля не только в неоднородной пороупругой среде ($0 < \alpha _{1}^{0} < 1$), в полностью упругой ($\alpha _{1}^{0} = 0$) или полностью жидкой среде ($\alpha _{1}^{0} = 1$), но и в любой комбинации этих сред. Покажем это на примере идеальной упругости. Действительно, для упругой среды $\alpha _{1}^{0} = 0$, $\alpha _{2}^{0} = 1$ система (1) преобразуется к виду:

где скорость смеси ${{v}^{i}} = с_{1}^{0}v_{1}^{i} + с_{2}^{0}v_{2}^{i} = v_{2}^{i}$ содержит только упругую фазу $v_{2}^{i}$, а объемный модуль $K$ совпадает с объемным модулем упругой фазы. Видно, что первое, третье и четвертое уравнения (2) являются точной формулировкой линейного вязкоупругого твердого тела Максвелла, записанного в терминах скоростей смещений/напряжений. Второе уравнение для ${{w}^{i}}$ является фиктивным и не оказывает никакого влияния на волны в упругой среде.

Если рассмотреть противоположную ситуацию $\alpha _{1}^{0} = 1$, $\alpha _{2}^{0} = 0$, которая соответствует случаю чистой жидкости, то (1) принимает вид:

где ${{v}^{i}}$ теперь соответствует скорости жидкости $v_{1}^{i}$, а объемный модуль $K$ равен объемному модулю жидкости. Первое и третье уравнения системы (3) образуют уравнения акустики жидкости, а второе и четвертое – фиктивные.

Как видим, система (1) дает универсальный способ моделирования волновых полей в образцах среды с резкими границами раздела петрофизических свойств: достаточно описать границы раздела в виде разрывной функции $\alpha _{{}}^{0}$. Такое описание интерфейсов называется методом диффузных границ. Заметим, что при моделировании двухфазных сжимаемых течений требуется разработка специальных численных приемов, позволяющих минимизировать численную диффузию движущихся границ раздела [9]. В нашем случае разрывы $\alpha _{{}}^{0}$ описывают лишь стационарные разрывы физических свойств внутри образца, поэтому нет необходимости заботиться о сохранении исходной формы разрыва по времени. Отметим, что метод диффузных границ также может быть применен к неоднородным образцам с резкими вариациями пористости.

ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ

Для симметрической гиперболической системы (1) использование конечно-разностных схем на сдвинутых сетках является наиболее эффективным в вычислительном плане подходом [10]. Нами используется схема на сдвинутых сетках четвертого порядка точности по пространству и второго порядка точности по времени.

Рассматривается слоистая среда Ω = [–0.025, 0.025]²м, содержащая одновременно три различных состояния: упругое, жидкое и пороупругое. Все физические параметры приведены в табл. 1. Упругий слой ($\alpha _{1}^{0} = 0$) находится вверху расчетной области, жидкий ($\alpha _{1}^{0} = 1$) – внизу, а пороупругий слой с пористостью $\alpha _{1}^{0} = 0.3$ располагается в среднем интервале [0, 0.015] м. В расчетах используется источник типа объемного расширения $F$:

где частота ${{f}_{0}}$ = 1 МГц и задержка импульса ${{t}_{0}} = 1{\text{/}}{{f}_{0}}$ с. Источник находится в упругом слое в точке $({{x}_{0}},{{y}_{0}})$ = (0, –0.015) м.

Для дискретизации используется квадратная сетка $Nx \times Ny$ с шагом $5 \times {{10}^{{ - 5}}}$ м, что составляет примерно 10 точек на длину медленной волны сжатия (волны Био) для выбранной частоты.

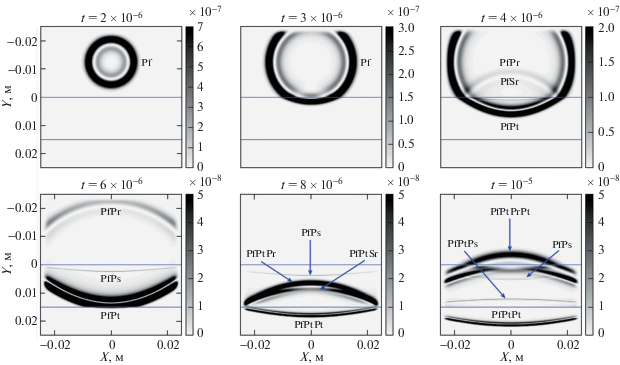
На рис. 1 приведены снимки волнового поля для квадрата модуля скорости ${{\left\| v \right\|}^{2}}$ в различные моменты времени. Для обозначения типов волн используются обозначения: буквы Р – для обозначения P-волн и S для обозначения S-волн, нижний индекс r – для обозначения отраженных волн, t – проходящих волн, s – медленной P-волны Био и f – исходной волны. В приведенном расчете наблюдаются все типы волн, предсказанные теорией упругости и пороупругости: корректное появление медленных Р-волн Био только в пористом слое и только волны давления в слое жидкости, в то время как в упругой среде наблюдаются волны сжатия и сдвига.

ЗАКЛЮЧЕНИЕ

Представлен метод диффузных границ для моделирования волновых полей в насыщенных упругих пористых средах. Определяющие уравнения являются гиперболической системой дифференциальных уравнений первого порядка и записаны в терминах скоростей смещений/напряжений, что позволяет использовать конечно-разностные схемы высокого порядка точности на сдвинутых сетках для численной аппроксимации. Предложенная система дает универсальный способ моделирования волновых полей в средах, имеющих резкие границы раздела упругих/пороупругих петрофизических свойств и, как и модель Био, предсказывает три типа волн: быстрые и медленные волны сжатия и поперечные волны. Численные расчеты показали хорошее качественное согласие с классической теорией упругости и моделью Био.