Электрохимия, 2019, T. 55, № 1, стр. 39-50
Развитие представлений о турбулентном течении в трубеДж. Ньюмен
Дж. Ньюмен *
Калифорнийский Университет
94720-1462 Калифорния, Беркли, США
* E-mail: newman@newman.cchem.berkeley.edu
Поступила в редакцию 09.02.2018
После доработки 18.04.2018
Принята к публикации 08.05.2018
Аннотация
В статье Никурадзе (1932 г.) о турбулентном течении в гладкой трубе имеется обширная информация о сопротивлении течению (коэффициент трения) и профилях скорости и вихревой вязкости. Задача настоящей работы – подробно изучить эту информацию с целью использовать ее в других ситуациях турбулентных течений. В частности, в реинжиниринге (обратной разработке) принято значение n = 2 для показателя степени объемного рассеяния в члене затухания уравнения диссипационной теоремы. Что также важно, интегрирование профилей вихревой вязкости по Никурадзе не приводит к его формуле универсального закона сопротивления; напротив, наличие вязкого подслоя оказывает очевидное влияние на результат, даже если принять, что на эту область влияет только тип массопереноса при высоких числах Шмидта. Предложена формула для затухания рассеяния в турбулентном потоке в гладкой трубе.
ВВЕДЕНИЕ
Диссипационная теорема отсылает нас к статистическому представлению турбулентности через напряжение Рейнольдса, объемное рассеяние – ${\mathbf{\tau }}:\nabla {\mathbf{v}},$ вихревую вязкость и кинетическую энергию на единицу объема. диссипационная теорема выведена в работе [1] в приложении к данным о массопереносе в системе вращающегося цилиндра. В работе [2] эти представления распространены на турбулентное течение в трубе. Одно из базовых уравнений диссипационной теоремы связывает объемное рассеяние с вихревой вязкостью. Для течения в трубе в безразмерной форме имеем:
где $D = {{\mu {{\mathcal{D}}_{V}}} \mathord{\left/ {\vphantom {{\mu {{\mathcal{D}}_{V}}} {\tau _{0}^{{\text{2}}}}}} \right. \kern-0em} {\tau _{0}^{{\text{2}}}}},$ ${{\mathcal{D}}_{V}}$ – рассеяние на единицу объема, μ – вязкость, а τ0 – напряжение сдвига у стенки трубы, R+ – это независимый параметр напряжения (R/ν)(τ0/ρ)0.5, а R+M – отношение ν(t)/ν вихревой кинематической вязкости к кинематической вязкости, ξ = r/R – это радиальное положение, деленное на радиус трубы. Второе базовое уравнение описывает, как объемное рассеяние меняется во времени и пространстве под действием конвекции, диффузии и затухания. Для стационарного полностью развитого течения в трубе это уравнение принимает следующий вид:(2)
$\frac{1}{\xi }\frac{\partial }{{\partial \xi }}\left( {{{\xi }^{3}}\frac{{\partial \ln D}}{{\partial \xi }}} \right) = \Lambda \frac{{{{D}^{n}}}}{{{{\xi }^{p}}{{{({{R}^{ + }})}}^{q}}}}\,\,{\text{ = }}\,\,{\text{з а т у х а н и е }}{\text{.}}$Уравнения (1) и (2) полностью тождественны уравнениям (49) и (50) работы [2]. Безразмерное затухание определяется левой частью уравнения [2]. Здесь Λ – безразмерная константа скорости, n – порядок реакции по затуханию, а два члена в знаменателе добавлены для того, чтобы добиться гибкости. Имеется еще и член 4, не показанный здесь, который, если его добавить, дает решение уравнения (2), описывающее ламинарное течение. При ξ = 1 (на стенке трубы) D = 1, а при ξ → 0 величина D становится пропорциональной ξ2.
Из турбулентного потока в трубе мы видим, что показатель степени, использованный в расходимости, должен оставаться равным 1, как это присуще цилиндрической геометрии, а не 5 для вращающегося цилиндра или –1 для потока в трубе. Более того, этот результат для вихревой вязкости должен позволять накладывать различные значения напряжения (по крайней мере, при высоких числах Рейнольдса), и это можно выполнить, вводя в член затухания множители с показателями степени p и q, соответственно, для радиального положения и для уровня напряжения (R+). Мы также лучше понимаем, как в вычислениях могут возникать отрицательные значения вихревой вязкости и как можно их избежать. Наша цель – выяснить, как применять аналогичные изменения в других ситуациях турбулентных потоков. Более того, из статьи Никурадзе (1932 г.) [3] можно получить еще больше полезной информации.
Мы сфокусируемся на потоке в трубе, имея дело с проблемами не вполне адекватно рассмотренными в работе [2]. Прежде всего, обратимся к графикам всех распределений Никурадзе вихревой вязкости при различных числах Рейнольдса, от 4000 до 3.2 × 106. Это покрывает интервал R+ от 112 до 56000.
Во всей области чисел Рейнольдса кривые имеют в основном одинаковую форму. Это означает, что профили вихревой вязкости приблизительно конгруэнтны, если разделить каждый из них на параметр напряжения R+. Эти профили полностью характеризуют поток. Например, коэффициент трения f дается формулой (B5), выведенной в Приложении B ,
(3)
$\sqrt {\frac{2}{f}} = {{R}^{ + }}\int\limits_0^1 {\frac{{{{\xi }^{3}}d\xi }}{{1 + {{R}^{ + }}M(\xi )}},} $Из рис. 1 ясно, что Никурадзе [3] считает, что вихревая вязкость не обнуляется на осевой линии потока. В свете доказательств того, что она должна стать равной нулю, приведенных автором (см. статью [2]), это может указывать на то, что поток не вполне развился, другими словами, что все еще остается какое-то влияние расстояния от входа в трубу. Следует отметить, что рис. 1 покрывает широкую область чисел Рейнольдса и несколько размеров трубы, и что следует обращать большее внимание на подобие этих профилей, чем на какие-то возможные случайные ситуации в развитии потока. (Это может побудить читателя быстрее перейти к последующим этапам настоящего исследования: развитие потоков на вращающемся диске или на плоской пластинке в месте падения потока или, как в рассматриваемом здесь примере, потоке в трубе). Может быть, следует иметь в виду утверждение Никурадзе о том, что вихревая вязкость не падает в точности до нуля на осевой линии. [Это наблюдение может иметь последствия для выбора между зависимостями типа y3 и y4 для затухания вихревой вязкости на стенке трубы. Аргумент в пользу выбора y4 зависит от того, полностью ли развился поток, и от независимости некоторых статистических усреднений от осевого расположения. Сильный аргумент в пользу выбора зависимости типа y3 основан на наблюдаемой зависимости числа Стантона от числа Шмидта в степени 2/3 (см., например, работу [1])].
Рис. 1.
Профили вихревой вязкости по Никурадзе для 16 различных чисел Рейнольдса. Пунктиром показана предельная кривая для больших чисел Рейнольдса. Точки для небольших чисел Рейнольдса лежат, в общем, слегка выше предельной кривой; a: числа Рейнольдса 4000, 6100, 9200 и16 700; б: числа Рейнольдса 23 300, 43 400, 105 000 и 205 000; в: числа Рейнольдса 396 000, 725 000, 1 110 000 и 1 536 000; г: высокие числа Рейнольдса 1 959 000, 2 350 000, 2 790 000 и 3 240 000.

ОБРАТНАЯ РАЗРАБОТКА (РЕИНЖИНИРИНГ) ДАННЫХ НИКУРАДЗЕ
Уже из рис. 9 работы [2] следует плодотворная идея: найти профиль объемного рассеяния, применив уравнение (1) к предельной кривой Никурадзе. Мы включили в данное сообщение Приложение A (ранее не публиковавшееся), поскольку оно очень хорошо описывает радиальное распределение D и ясно показывает, что поведение D различается в целом ряде областей. Подобная же обратная разработка помогает выявить и форму члена затухания. Профиль вихревой вязкости по Никурадзе можно аппроксимировать, пользуясь следующей формулой:
(4)
$M = {{{{\nu }^{{(t)}}}} \mathord{\left/ {\vphantom {{{{\nu }^{{(t)}}}} {\nu {{R}^{ + }}}}} \right. \kern-0em} {\nu {{R}^{ + }}}} = 0.08 - 0.3843{{\left| {\xi - 0.48} \right|}^{{2.4}}}.$Фитинг кривой для ее обнуления на оси трубы таков:
(5)
${{{{\nu }^{{(t)}}}} \mathord{\left/ {\vphantom {{{{\nu }^{{(t)}}}} {\nu {{R}^{ + }}}}} \right. \kern-0em} {\nu {{R}^{ + }}}} = 0.08 - 0.4224{{\left| {\xi - 0.5} \right|}^{{2.4}}}.$Эта обратная разработка включает нахождение D путем подстановки уравнения (4) в уравнение (1) и последующей подстановки полученного результата в уравнение (2), с тем, чтобы получить затухание. Это дает множество значений для члена затухания для тех положений и чисел Рейнольдса, которые используются в работе Никурадзе, а также дает некоторое указание на то, каким было бы подходящее представление члена затухания в качестве функции объемного рассеяния. Ниже приводятся некоторые из необходимых производных.
(6)
$\begin{gathered} \frac{{\partial D}}{{\partial \xi }} = \frac{{2\xi }}{{1 + M{{R}^{ + }}}} - \frac{{{{\xi }^{2}}}}{{{{{[1 + M{{R}^{ + }}]}}^{2}}}}{{R}^{ + }}\frac{{\partial M}}{{\partial \xi }} = \\ = \frac{{2D}}{\xi } - \frac{{{{D}^{2}}}}{{{{\xi }^{2}}}}{{R}^{ + }}\frac{{\partial M}}{{\partial \xi }}, \\ \end{gathered} $(7)
$\begin{gathered} \frac{{{{\partial }^{2}}D}}{{\partial {{\xi }^{2}}}} = \frac{2}{{1 + M{{R}^{ + }}}} - \frac{{4\xi }}{{{{{[1 + M{{R}^{ + }}]}}^{2}}}}{{R}^{ + }}\frac{{\partial M}}{{\partial \xi }} + \\ + \,\,\frac{{2{{\xi }^{2}}}}{{{{{[1 + M{{R}^{ + }}]}}^{3}}}}{{\left( {{{R}^{ + }}\frac{{\partial M}}{{\partial \xi }}} \right)}^{2}} - \frac{{{{\xi }^{2}}}}{{{{{[1 + M{{R}^{ + }}]}}^{2}}}}{{R}^{ + }}\frac{{{{\partial }^{2}}M}}{{\partial {{\xi }^{2}}}} = \\ = \frac{{2D}}{{{{\xi }^{2}}}} - \frac{{4{{D}^{2}}}}{{{{\xi }^{3}}}}{{R}^{ + }}\frac{{\partial M}}{{\partial \xi }} + \\ + \,\,\frac{{2{{D}^{3}}}}{{{{\xi }^{4}}}}{{\left( {{{R}^{ + }}\frac{{\partial M}}{{\partial \xi }}} \right)}^{2}} - \frac{{{{D}^{2}}}}{{{{\xi }^{2}}}}{{R}^{ + }}\frac{{{{\partial }^{2}}M}}{{\partial {{\xi }^{2}}}}. \\ \end{gathered} $Без оглядки на знак при абсолютной величине, можно записать производные от M следующим образом:
(8)
$\frac{{\partial M}}{{\partial \xi }} = - 0.38431 \times 2.4{{\left| {\xi - 0.48} \right|}^{{1.4}}},$(9)
$\frac{{{{\partial }^{2}}M}}{{\partial {{\xi }^{2}}}} = - 0.38431 \times 2.4 \times 1.4{{\left| {\xi - 0.48} \right|}^{{0.4}}}.$Знак первой из этих производных меняется при ξ = 0.48. Возможно, следует провести заново фитинг предельной кривой Никурадзе с использованием ряда четных показателей степени ξ для того, чтобы избавиться от этого (возможно, не имеющего физического смысла) дробного показателя степени 2.4.
Таким образом, можно записать затухание (в безразмерной форме), как
(10)
${\text{з а т у х а н и е }} = {\text{3}}\left( {\frac{\xi }{D}\frac{{\partial D}}{{\partial \xi }}} \right) - {{\left( {\frac{\xi }{D}\frac{{\partial D}}{{\partial \xi }}} \right)}^{2}} + \,\,\frac{{{{\xi }^{2}}}}{D}\frac{{{{\partial }^{2}}D}}{{\partial {{\xi }^{2}}}}.$Подстановка уравнений (8) и (9) дает:
(11)
$\begin{gathered} {\text{з а т у х а н и е }} = 4 - 3\left( {\frac{{D{{R}^{ + }}}}{\xi }\frac{{\partial M}}{{\partial \xi }}} \right) + \\ + \,\,{{\left( {\frac{{D{{R}^{ + }}}}{\xi }\frac{{\partial M}}{{\partial \xi }}} \right)}^{2}} - D{{R}^{ + }}\frac{{{{\partial }^{2}}M}}{{\partial {{\xi }^{2}}}}. \\ \end{gathered} $Этот подход реализован в форме электронной таблицы, представленной на рис. 2.
Рис. 2.
Безразмерное затухание, вычисленное путем обратной разработки предельной кривой для вихревой вязкости для потока в трубе, экспериментально измеренного Никурадзе, и фитинг Дж. Ньюмена. Точечной кривой показана близкая аппроксимация. Пунктирная кривая показывает, что при больших значениях R+D наклон равен 2. Рассчитанные кривые накладываются друг на друга при трех значениях R+. Две аппроксимации накладываются друг на друга при двух значениях R+.

Прежде всего, рис. 2 ясно свидетельствует о том, что член затухания должен быть пропорционален D2, в частности, при больших значениях R+D, которые представляют наибольший интерес вблизи стенки, где объемное рассеяние резко снижается. Этот рисунок также позволяет предположить, что член затухания зависит только от R+D. Во-вторых, рис. 2 подтверждает идею о том, что член 4 следует включать в член затухания при малых значениях R+D, несмотря на то, что он может быть несущественным при высокой турбулентности. Этот член плохо работает при воспроизведении формы кривых Никурадзе для вихревой вязкости на рис. 1, несмотря на то, что он возникает при обратной разработке его предельной кривой. Это приближение (представленное точечной кривой на рис. 2) таково:
(12)
${\text{а п п р о к с и м а ц и я з а т у х а н и я }} = 4 + {{\left( {\frac{{D{{R}^{ + }}}}{\xi }\frac{{\partial M}}{{\partial \xi }}} \right)}^{2}}.$Таким образом, опущены два существенных члена из уравнения (11). Соответственно, третий урок, который мы можем извлечь из рис. 2, заключается в том, что член затухания включает явную зависимость от ξ (что может быть результатом локального напряжения), что еще удивительнее, он включает зависимость и от производной dM/dξ. Обычно мы не думаем о том, что член затухания связан с этой производной, предполагая нелокальную зависимость. [Нас беспокоит подобное же появление производной химического потенциала в теории Кана–Хиллиарда [4] о распределении по размеру капелек, образующихся в результате сверхкритической конденсации.] Можно опять скомбинировать R+ с производной и сказать, что доказана зависимость затухания от производной ν(t), что переносится на производную от D по уравнениям (1) или (6) [(см. уравнение (10).] Другая полезная аппроксимация затухания такова:
(13)
${\text{а п п р о к с и м а ц и я з а т у х а н и я }} = 4 + 0.17{{\left( {\frac{{D{{R}^{ + }}}}{\xi }} \right)}^{2}}.$Она в точности соответствует тому, что мы получили путем сравнения различных форм с проведенным Никурадзе экспериментальным определением коэффициента трения в потоке в трубе. Здесь производная от M исчезает, и значение Coef берется равным 0.17. Таким образом, мы приходим к заключению о том, что n = 2, по крайней мере, в потоке в трубе.
Однако, уравнение (13) приводит к отрицательным значениям вихревой вязкости вблизи центральной линии и при малых R+, и в общем виде к нулевому значению вихревой вязкости на оси, как в уравнении (5). Это заставляет нас считать, что, возможно, Никурадзе прав в том, что вихревая вязкость не падает в точности до нуля на центральной линии.
Эта мысль вызывает новые идеи насчет того, как повлиять на форму кривой. Одна из них – взять показатель степени n равным 2 (что может дать прямые линии на графике универсального сопротивления), но также показатель степени 1, что может быть ближе к затуханию гомогенной изотропной турбулентности на финальных стадиях. Это можно выразить следующим уравнением:
(14)
$\begin{gathered} {\text{а п п р о к с и м а ц и я з а т у х а н и я }} = \\ = {{C}_{2}}{{\left( {{{{{R}^{ + }}D} \mathord{\left/ {\vphantom {{{{R}^{ + }}D} \xi }} \right. \kern-0em} \xi }} \right)}^{2}} + {{C}_{1}}{{{{R}^{ + }}D} \mathord{\left/ {\vphantom {{{{R}^{ + }}D} \xi }} \right. \kern-0em} \xi }, \\ \end{gathered} $Удивительная вещь, вытекающая из работы Никурадзе – это то, что производная от M на стенке трубы не чувствительна к значению R+. Это согласуется с более ранней работой из 1920-х гг. об универсальном профиле скорости. Это – необходимое условие для достоверности закона универсального сопротивления, с которым мы имеем дело в Приложении В. Возможно, это не применимо к другим турбулентным течениям.
Для потока в трубе имеем ${{\bar {\tau }}_{{rz}}}$= τ0r/R = ξτ0. Отсюда, мы можем связать появление величины ξ в выражении для затухания с членом локального напряжения в знаменателе. Таким образом, мы можем выразить приближенно член затухания следующим уравнением:
(15)
$\begin{gathered} {\text{З а т у х а н и е }}\,\,{\text{в }}\,\,{\text{р а з м е р н ы х }}\,\,{\text{е д и н и ц а х }} = \\ = \frac{{\tau _{{\text{0}}}^{{\text{2}}}}}{{\rho {{R}^{{\text{2}}}}}}{\text{з а т у х а н и е }} \approx \frac{{k{{\tau }_{{\text{0}}}}}}{\rho }{{\left( {\frac{{\mu {{\mathcal{D}}_{V}}}}{{R{{{\bar {\tau }}}_{{rz}}}}}} \right)}^{2}}. \\ \end{gathered} $Локальное напряжение для вращающихся цилиндров зависит от радиального положения отличным образом $\left( {{{{\bar {\tau }}}_{{r{\theta }}}} = {{{{\tau }_{i}}} \mathord{\left/ {\vphantom {{{{\tau }_{i}}} {{{\xi }^{2}}}}} \right. \kern-0em} {{{\xi }^{2}}}}} \right),$ и здесь связь ξ с локальным напряжением может быть полезной. Принципиальное различие между течением в трубе и вращающимися цилиндрами как раз и заключается в зависимости локального напряжения от радиального положения.
РЕЗУЛЬТАТЫ, ПОЛУЧЕННЫЕ С ИСПОЛЬЗОВАНИЕМ ДИССИПАЦИОННОЙ ТЕОРЕМЫ
На рис. 3 показаны графики распределения вихревой вязкости, предсказанные на основе диссипационной теоремы. [Уравнение (14) использовано в форме, эквивалентной замене D n на D n + εD в члене затухания, где ε = C3/R+. Это не в точности то же самое, и нам требуется точно знать, как мы хотели бы записать уравнение (14).] У этих графиков хорошая форма (для n = 2), но они не такие “тучные”, как профили Никурадзе, представленные на рис. 1. Они не воспроизводят нулевого значения вихревой вязкости на центральной линии. При n = 2 эти профили дают график коэффициента трения с прямой линией при больших числах Рейнольдса, если строить его по типу закона универсального сопротивления. С другими значениями n трудно добиться такой же прямой линии. В попытках изменить форму распределения вихревой вязкости мы добавили член, позволяющий ламинарному потоку стать решением дифференциального уравнения рассеяния. Как будет показано ниже, такое модифицирование профиля вихревой вязкости не оказывает существенного влияния на форму зависимости коэффициента трения от Re или R+. [Пунктирной линией на рис. 3 показано, чтó мы получили, добавив член 4].
Рис. 3.
Профили вихревой вязкости, рассчитанные с использованием диссипационной теоремы. Верхние сплошные кривые рассчитаны со следующими параметрами: Coef = 0.17, n = p = q =2, B+ = 0.0005, ε = = 0.33/R+. Кривые для значений R+, равных 88198, 16399, 3049 и 567, накладываются друг на друга, в то время, как кривая для 105 проходит слегка ниже. (Напротив, экспериментальные данные Никурадзе для низких R+ на рис. 1 оказываются выше его предельной кривой.) Эти сплошные кривые рассчитаны с использованием диссипационной теоремы без какого-либо учета вязкого подслоя. Точечные кривые для R+ = 567 и 105 демонстрируют влияние “сращивания” в вязком подслое. При R+ = 105 это распространяется от r/R = 1 до, приблизительно, 0.8, но в гораздо меньшей степени, чем для R+ = 567. Слева кривые очень похожи на кривые Никурадзе из рис. 1 тем, что они не идут в нуль на оси. Это достигается с помощью параметра ε, введенного в настоящей работе. Пунктирные кривые получаются, когда в безразмерный член затухания в диссипационном уравнении добавляется член 4.

КАК ИЗБЕЖАТЬ ОТРИЦАТЕЛЬНОЙ ВИХРЕВОЙ ВЯЗКОСТИ
При построении рис. 3 и выполнении вычислений по диссипационной теореме получались и отрицательные значения вихревой вязкости вблизи оси трубы и при низких значениях R+. Это происходило и с членом затухания, который выглядит в соответствии с уравнением (13) (с добавленным членом 4 или без него). Должен существовать физический механизм, предотвращающий появление отрицательных значений. В этом отношении более многообещающими выглядят профили Никурадзе на рис. 1 с ненулевой вихревой вязкостью на оси. Это видно на рис. 4, где использовано уравнение (1) для вычисления рассеяния из предельной кривой Никурадзе [уравнение (4)] и из этой же кривой, если принудительно положить вихревую вязкость равной нулю на оси [уравнение (5)].
Рис. 4.
Сплошные кривые представляют объемное рассеяние, вычисленное по уравнению (1) из предельной кривой Никурадзе для вихревой вязкости, представленной уравнением (4). Точечные кривые рассчитаны таким же способом, но по уравнению (5), причем вихревая вязкость принудительно обращается в нуль на оси. Пунктирная кривая – это кривая для ламинарного течения; она неизбежно приводит к нулевой вихревой вязкости. Соответственно, пересечение кривой для ламинарного течения приводит к отрицательным значениям вихревой вязкости. Все кривые начинаются при 1 на стенке (r/R = 1). Более высокие значения R+ вызывают более крутой скачок объемного рассеяния и при этом отстоят дальше от области отрицательной вихревой вязкости. Однако, кривые с отрицательной вихревой вязкостью на центральной линии асимптотически приближаются к кривой для ламинарного течения вблизи оси. Это означает, что программа рассеяния, которая предсказывает поведение вихревой вязкости, имеет бóльшую вероятность приблизиться к кривой для ламинарного течения.

Изначально мы ожидали, что вихревая вязкость достигнет своего максимума на центральной линии, но экспериментальные результаты Никурадзе (рис. 1) показали, что на самом деле вихревая вязкость проходит через максимум и приближается к небольшому, но ненулевому значению на оси. Затухание возрастает, когда рассеяние велико у стенки, и оно возрастает еще быстрее вблизи оси (благодаря присутствию величины ξ2 в знаменателе). Форма кривых рассеяния на рис. 4 отражает уменьшение D по направлению к оси, но также и увеличение затухания благодаря радиальному положению. Когда D становится очень маленьким, затухание тоже становится маленьким, и кривая может пересечь кривую для ламинарного течения.
Моя аргументация такова: член затухания не должен продолжать уменьшаться по закону D2 вблизи оси; член затухания уменьшаться с D только по линейному закону на последних этапах затухания. Такова причина введения члена, содержащего εD. Применение такого подхода при построении рис. 3 позволило достичь согласования с Никурадзевским ненулевым значением вихревой вязкости на оси, и это также позволило избежать отрицательных значений вихревой вязкости вблизи оси при низких значениях R+. Эмпирический фитинг говорит о том, что величина ε должна быть обратно пропорциональна R+. (Эти параметры не изменились при построении пунктирных кривых с добавлением члена 4 в затухании. Соответственно, вихревая вязкость спадает ниже значений Никурадзе на оси, и для сáмого низкого значения R+ вблизи оси были получены отрицательные значения.)
Дальнейшее изучение этих вопросов заставляет нас заново рассмотреть член затухания. Уравнение (11) показывает, что имеется доминантный член, пропорциональный (R+D)2, но также есть еще два члена, пропорциональных R+D. Можно полагать, что производные от M следует действительно оценивать вблизи стенки. Тогда dM/dξ = = ‒β0 ≈ –0.36823, а d2M/dξ2 равняется приблизительно –0.994, так что следует брать полное выражение (9): затухание ≈ 4 + (β0R+D/ξ)2 + 3β0R+D/ξ + + 0.994R+D. Это приводит к мысли о том, что Coef приблизительно равняется $\beta _{0}^{{\text{2}}},$ соответственно, член пропорционален R+D. Но мы все же будем продолжать использовать для этих коэффициентов эмпирические константы.
ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА ТРЕНИЯ ИЗ ЗАДАННОГО РАСПРЕДЕЛЕНИЯ ВИХРЕВОЙ ВЯЗКОСТИ
Уравнение (3) позволяет рассчитать коэффициент трения непосредственно из вихревой вязкости. В Приложении B показано, как использовать это уравнение для того, чтобы вывести формулу универсального сопротивления. Здесь мы рассмотрим, как провести расчеты численно и при этом корректно учесть тот факт, что подынтегральное выражение резко меняется при малых значениях 1 – ξ, от 1 при ξ = 1 и до намного меньшей величины при больших значениях R+. Если отложить подынтегральное выражение, как функцию R+(1 – ξ), то при малых величинах абсциссы кривые для различных R+ совмещаются. Наш подход заключается в том, чтобы использовать для первого шага шаг малого размера h [например, 0.001/R+], а затем увеличивать шаги на множитель 1.05 для каждого последующего шага. Это позволяет провести точное интегрирование для малых значений абсциссы, удерживая при этом полное число шагов умеренным при больших значениях R+. Результирующий график, построенный, как предложено выше, на основе закона универсального сопротивления, – это нижние кривые на рис. 5. [Эта новая разрядка точек дает недостаточную точность вблизи от ξ = 0, где при малых значениях R+ может возникать отрицательная вихревая вязкость. Это не создает проблем там, где вихревая вязкость известна или задана, но может стать проблемой, если использовать для предсказания вихревой вязкости диссипационную теорему.]
Рис. 5.
Вычисление коэффициента трения из распределения вихревой вязкости. Кривая внизу получена непосредственным интегрированием уравнения (3) по измерениям вихревой вязкости, выполненным Никурадзе, с меньшим размером шага при бóльших значениях R+. Другая кривая вычислена на основе программы рассеяния с существенным использованием профилей вихревой вязкости (рис. 3), но с включением области y3, т.е. вязкого подслоя. Эта кривая поднимается от нижней кривой и в конце концов приближается к прямой линии, лежащей намного выше асимптоты нижней кривой. (Здесь Coef = 0.17, n = p = q = 2, B+ = 0.0005. Кривая не модифицирована при ненулевой величине ε и обработана, как на рис. 3.) Прямые линии таковы: (2/f)0.5 = = 2.7ln(R+) – 6.46 для нижней линии и 2.45 ln(R+) + 2 для верхней линии, что хорошо согласуется с фитингом Никурадзе экспериментальных данных по коэффициенту трения с помощью графика универсального сопротивления [см. уравнение (B2)].

Расхождение между двумя методами расчета коэффициента трения проясняется при тщательном анализе деталей интегрирования. Существует различие между профилями вихревой вязкости в области y3 очень близкой к стенке (см. подробное описание в работе [1]). Для получения нижней кривой использовали уравнение (3) при непосредственном интегрировании профилей вихревой вязкости по Никурадзе, как дается уравнением (4). Для области y3 не принято ограничений, и кривая оказывается намного ниже верхней пунктирной линии, показывая, как Никурадзе проводил фитинг своих экспериментальных данных по коэффициенту трения с законом универсального сопротивления. Верхняя кривая вычислена с помощью диссипационной теоремы [уравнения (1) и (2)] с одним или двумя подгоночными параметрами и автоматическим включением области y3.
Другие кривые (не включенные в этот рисунок, чтобы не загромождать его) могут использовать профили вихревой вязкости по Никурадзе, но без области y3. Это вполне объясняет различие между кривыми на рис. 5.
Результат, вытекающий из обсуждения рис. 5, поразителен. Мы приняли, что область y3 настолько мала, что она оказывает влияние на массоперенос главным образом при высоких числах Шмидта, при которых можно исследовать внутреннюю часть диффузионного слоя у стенки. Можно заключить, что она не оказывает существенного влияния на гидродинамику, поскольку это влияние воплощено в коэффициенте трения. Мы включили область y3 в программу рассеяния, которая также используется для предсказания результатов массопереноса, и использованный параметр (B+ = 0.0005) – это “остаток” такого подхода к исследованию. Более ранний вывод (о том, что вязкий подслой не влияет на гидродинамику и на коэффициент трения) оказывается неверным. На самом деле интегрирование профиля вихревой вязкости, как следует из рис. 1, не дает коэффициента трения, как предполагает график универсального сопротивления (или график зависимости коэффициента трения от числа Рейнольдса). Область y3, какой бы узкой она ни была, все же представляет достаточное гидродинамическое сопротивление для того, чтобы сильно изменить отрезок, отсекаемый на координатной оси в графике закона универсального сопротивления (от, приблизительно, –6.46 до +2). Изменение B+ от 0.0005 до 0.0002 или 0.001 сильно меняет верхнюю кривую. (В качестве альтернативы можно принять существование области y4 и поместить кривую выше кривой, отвечающей области y3. Выбрать между использованием областей y3 или y4 не позволяет недостаточное разрешение.)
Этот вывод мы распространим следующим образом: вязкий подслой оказывает огромное влияние на коэффициент трения; это важное открытие, сделанное в настоящей работе. Ретроспективно, кажется само собой, что это утверждение верно, потому что коэффициент трения (или напряжение на стенке) получается прямым интегрированием профиля вихревой вязкости. Тем не менее, в общем случае мы считаем, что вязкий подслой проявляется в массопереносе при высоких числах Шмидта. Это происходит главным образом, когда число Шмидта приближается к нулю, аналогия Рейнольдса применима, а число Стантона приблизительно равняется коэффициенту трения (больше 2), в то время, как при высоких числах Шмидта произведение чисел Стантона и Шмидта в степени 2/3 или 3/4 пропорционально корню квадратному из коэффициента трения. Никурадзе прекрасно измерил распределение вихревой вязкости. Вязкий подслой никак не проявляется. Никурадзе способствовал разработке метода на основе закона универсального сопротивления, строя графики коэффициента трения вышеописанным способом. Поэтому явилось некоторым сюрпризом то, что при интегрировании его данных по вихревой вязкости его кривая коэффициента трения не воспроизвелась. Ну и ну!
РАСХОЖДЕНИЯ
Никурадзе показал существование ненулевой вихревой вязкости на центральной линии, вопреки диссипационной теореме. Такое расхождение можно устранить, модифицируя член затухания с тем, чтобы воспроизвести ненулевые значения вихревой вязкости по Никурадзе на оси. Никурадзе показал, что коэффициент трения все время следует асимптотической формуле закона универсального сопротивления вплоть до R+ = 112, в то время, как диссипационная теорема демонстрирует отрицательное отклонение (см. рис. 5). При низких значениях R+ Никурадзевские значения ν(t)/νR+ имеют тенденцию ложиться выше предельной кривой, в то время как значения на основе диссипационной теоремы ложатся ниже ее (сравн. рис. 1 и 3).
Член затухания, как кажется, требует дополнительного члена 4 для того, чтобы дать возможность удовлетворить уравнению диссипационной теоремы с помощью Пуазейлевского результата для ламинарного течения. Он также возникает при обратной разработке предельной формы для вихревой вязкости по Никурадзе. Однако, он оказывается пренебрежимо мал при высоких уровнях турбулентности, и он может вызывать такие профили вихревой вязкости, которые расходятся с теми, что измерил Никурадзе (см. рис. 3).
Вязкий подслой пока еще не интегрирован с другими областями, в том смысле, что у нас нет определяющего уравнения для нахождения коэффициента при члене y3, даже при очевидности того, что вязкий подслой зависит от областей, отстоящих дальше от стенки, и тесно связан с этими областями. Вихри во внешнем течении имеют значительный размер. При приближении к стенке они должны уменьшаться по величине. Это явствует из того, что средняя тангенциальная скорость приближается к нулю по линейному закону по мере приближения к стенке, а средняя скорость по нормали приближается к нулю по квадратичному закону, как требует уравнение непрерывности. Вблизи стенки приближение к нелинейной природе турбулентности осуществляется с помощью главенства линейных уравнений. Статистические теории турбулентности должны помочь в выводе соотношения между параметрами B+ (характеризующим вязкий подслой) и $B_{{\text{1}}}^{ + }$ (расчетным параметром, характеризующим флуктуации дальше от поверхности, как предсказано диссипационной теоремой), см., например, работу [5]. В настоящей работе мы не ставили целью осуществлять этот подход.
Несмотря на эти расхождения, согласие между диссипационной теоремой и результатами наблюдений продолжает укрепляться.
ЗАКЛЮЧЕНИЕ
Вихревая вязкость, как оказывается, не обнуляется на оси течения в трубе, а сохраняет некоторое малое значение. Коэффициент трения может быть точно вычислен интегрированием профиля вихревой вязкости, но для того, чтобы добиться согласия с экспериментом, требуется включить в расчеты вязкий подслой очень близко к твердой стенке трубы. Можно вывести линейное (асимптотическое) соотношение между обратной величиной корня квадратного из коэффициента трения и логарифмом параметра напряжения R+ путем тщательного исследования формы вихревой вязкости вблизи твердой стенки. С помощью обратной разработки можно получить лучшие представления о поведении члена затухания в диссипационной теореме, показав при этом, что наилучшее значение n равняется 2 для показателя степени при объемном рассеянии. Надо надеяться, что настоящая работа приведет к лучшему пониманию роли члена затухания в ситуациях с другими течениями, включая вращающиеся цилиндры и развивающиеся турбулентные течения.
ПРИЛОЖЕНИЕ A . ОБРАБОТКА МЕТОДОМ СИНГУЛЯРНЫХ ВОЗМУЩЕНИЙ
Рисунок 1 в статье Никурадзе ясно показывает, что вихревую вязкость можно аппроксимировать следующим образом:
где C ≈ 0.32, а ξ = r/R. Эта формула оказывается равно справедливой на стенке, в объеме и в центральных зонах, то есть, везде, за исключением вязкого подслоя. (Мы используем значение C = = 0.3 там, где нам потребуется численное значение.) Формула (1) показывает интересные подробности, касающиеся профиля объемного рассеяния.Рисунок A1 показывает, что центральная зона и объем могут перекрываться, если мы используем R+ξ для напряженной радиальной переменной и (R+)2D для напряженной диссипативной переменной. Рисунок A2 показывает, что область объема и область стенки могут перекрываться, если мы используем y+ = R+(1 – ξ) для напряженной радиальной переменной и D для напряженной диссипативной переменной.
Рис. A1.
Наложение значений рассеяния в центральной зоне и в объеме с использованием подходящих напряженных переменных. В объеме D = ξ/0.3R, а в центральной зоне D = ξ2. В краевой области заметно отклонение от такого поведения.

Рис. A2.
Наложение значений рассеяния в объеме и в пристенной области с использованием подходящих напряженных переменных. В объеме D = 1/0.3y+, а в пристенной области D = 1/(1 + 0.3y+). В центральной зоне заметно отклонение от такого поведения.

Уравнение (1) – общее уравнение для потока в трубе. В объеме ν(t)$ \gg $ ν, если R+ велико, а наиболее подходящая форма для D такова:
Таким образом, D = O(1/R+), а ξ = O(1). Поскольку ξ → 0,то при приближении к центральной зоне имеем D → ξ/CR+, а поскольку ξ → 1, то при приближении к области стенки D → 1/Cy+. Эти формы будут использованы при согласовании области объема с центральной зоной или областью стенки. В связи с рис. 3 следует отметить, что в области объема DR+ = O(1).
Напряженная координата в центральной зоне равняется $\bar {\xi }$= R+ξ, а подходящая форма для D такова:
(A4)
$D = \frac{{{{{{{\bar {\xi }}}^{2}}} \mathord{\left/ {\vphantom {{{{{\bar {\xi }}}^{2}}} {{{{({{R}^{ + }})}}^{2}}}}} \right. \kern-0em} {{{{({{R}^{ + }})}}^{2}}}}}}{{1 + C\bar {\xi }}}.$Таким образом, D = O(1/(R+)2), а ξ = O(1/R+). Если $\bar {\xi }$ → ∞, т.е. при приближении к объему, D → → $\bar {\xi }$/C(R+)2, демонстрируя соответствие между этими двумя областями.
Напряженная координата в области стенки равняется y+= R+(1 – ξ), а подходящая форма для D такова:
Таким образом, D = O(1), а 1 – ξ = O(1/R+). При y+ → ∞, т.е. при приближении к объему, D → → 1/Cy+, демонстрируя соответствие между этими двумя областями. Отметим, что здесь ясно видно, что толщина области стенки равняется Δξ = O(1/R+).
Можно ожидать, что эти порядки величин останутся теми же, если вместо уравнения (A1) для вихревой вязкости мы используем диссипационную теорему. Эти выводы также должны сохранить свою справедливость, если вместо уравнения (A1) использовать уравнения (4) или (5). Область y3 (которая в данном случае может превратиться в область y4, см. Приложение A работы [2]) можно рассматривать, как часть области применимости закона стенки, а y+ все еще может служить в качестве напряженной переменной. Однако, мы рассматриваем область y3 как отдельную, поскольку в настоящее время отсутствует какой-либо способ обсчитывать ее на основе диссипационной теоремы. В этой области не существует обоснованного определяющего уравнения. Объем – это область, в которой ν(t)$ \gg $ ν, в то время, как в пристенной области ν(t) ≈ ν. Если ν(t) обнуляется на центральной линии, то можно сказать, что центральная зона есть область, в которой ν(t) ≈ ν. Однако, поскольку вихревая вязкость не обращается в нуль на осевой линии (рис. 1), это утверждение больше не является верным, и центральную зону следует определить как область, в которой объемное рассеяние пропорционально to ξ2.
Несмотря на то, что сказано в этом Приложении, рис. 4 показывает, что поведение D разительно отличается, если мы используем уравнение (4) вместо уравнения (5). Кривые для D все еще резко спадают, но их наклон уменьшается до 2, а затем кривая становится параллельной линии для ламинарного течения, вместо того, чтобы наклониться и приблизиться к линии для ламинарного течения асимптотически. Таким образом, в этом случае отсутствует область с наклоном, равным 1.
ПРИЛОЖЕНИЕ B . ФОРМУЛА ДЛЯ УНИВЕРСАЛЬНОГО СОПРОТИВЛЕНИЯ
Для потока в трубе формула для универсального сопротивления представляет обратную величину корня квадратного из коэффициента трения как линейную функцию логарифма числа Рейнольдса, умноженного на корень квадратный из коэффициента трения. Это неправдоподобное соотношение можно представить себе проще: как линейное соотношение между обратной величиной корня квадратного из коэффициента трения и логарифмом параметра напряжения R+. Это может быть перенесено на систему вращающегося цилиндра и на массоперенос, по крайней мере, при высоких числах Шмидта (см. работы [1] и [2]).
И Никурадзе, и некоторые авторы до него понимали, что коэффициент трения всегда имеет меньший наклон при бóльших числах Рейнольдса, будучи отложен логарифмически, но что прямая линия получается, если отложить данные, как указано выше. Никурадзе распространил экспериментальные числа Рейнольдса на бóльшие значения и нашел новое асимптотическое распределение для профилей вихревой вязкости и скорости и для коэффициента трения. Он выразил степень соответствия своих данных для скорости течения и скачка давления, как
(B1)
${1 \mathord{\left/ {\vphantom {1 {\sqrt {4f} }}} \right. \kern-0em} {\sqrt {4f} }} = 2.0\lg (\operatorname{Re} \sqrt {4f} ) - 0.8,$(B2)
$\sqrt {{2 \mathord{\left/ {\vphantom {2 f}} \right. \kern-0em} f}} = 2.457\ln ({{R}^{ + }}) + 1.9945.$Прямую линию для больших значений R+ можно получить следующим образом. Из уравнения (17) работы [2] получаем среднюю скорость:
(B3)
$\left\langle {{{{{\bar {v}}}}_{z}}} \right\rangle = \frac{2}{{{{R}^{2}}}}{\text{ }}\int\limits_0^R {{{{{\bar {v}}}}_{z}}rdr} = \frac{{{{\tau }_{0}}}}{{{{R}^{3}}}}\int\limits_0^R {\frac{{{{r}^{3}}dr}}{{\mu + {{\mu }^{{(t)}}}}}} .$Re, R+ и f определяются, как
(B4)
$\operatorname{Re} = \frac{{2R\left\langle {{{{{\bar {v}}}}_{z}}} \right\rangle }}{\nu },{\text{ }}{{R}^{ + }} = \frac{R}{\nu }\sqrt {\frac{{{{\tau }_{0}}}}{\rho }} {\text{ и }}f = \frac{{2{{\tau }_{0}}}}{{\rho {{{\left\langle {{{{{\bar {v}}}}_{z}}} \right\rangle }}^{2}}}},$(B5)
$\sqrt {\frac{2}{f}} = {{R}^{ + }}\int\limits_0^1 {\frac{{{{\xi }^{3}}d\xi }}{{1 + {{R}^{ + }}M(\xi )}},{\text{ г д е }}\xi = {r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R}.} $Для вращающегося цилиндра действует несколько иная формула. Даже при больших значениях R+ нельзя просто напросто пренебречь единицей в знаменателе, поскольку на стенке трубы M падает до нуля, ξ = 1. Для учета сингулярности положим
где β0 – отрицательная величина производной от M при ξ = 1. Теперь прибавим и вычтем сингулярную часть подынтегрального выражения, так что уравнение (B5) примет вид(B7)
$\begin{gathered} \sqrt {\frac{2}{f}} = {{R}^{ + }}\int\limits_0^1 {\left[ {\frac{{{{\xi }^{3}}}}{{1 + {{R}^{ + }}M(\xi )}} - \frac{{{{\xi }^{3}}}}{{1 + {{\beta }_{0}}{{R}^{ + }}(1 - \xi )}}} \right]d\xi + } \\ + \,\,{{R}^{ + }}\int\limits_0^1 {\left[ {\frac{{{{\xi }^{3}}d\xi }}{{1 + {{\beta }_{0}}{{R}^{ + }}(1 - \xi )}}} \right]} . \\ \end{gathered} $Сначала займемся вторым интегралом. Подставим x = 1 + B(1 – ξ), где B обозначает β0R+ и считается большой величиной:
(B8)
$\begin{gathered} {{I}_{2}} = \frac{B}{{{{\beta }_{0}}}}\int\limits_0^1 {\frac{{{{\xi }^{3}}d\xi }}{{1 + B(1 - \xi )}} = } \\ = \frac{1}{{{{B}^{3}}{{\beta }_{0}}}}\int\limits_1^{1 + B} {{{{\left[ {B - x + 1} \right]}}^{3}}\frac{{dx}}{x}} = \\ = \frac{1}{{{{B}^{3}}{{\beta }_{0}}}}\int\limits_1^{1 + B} {\left[ {{{{(B + 1)}}^{3}} - 3x{{{(B + 1)}}^{2}} + } \right.} \\ \left. { + \,\,3{{x}^{2}}(B + 1) - {{x}^{3}}} \right]\frac{{dx}}{x}. \\ \end{gathered} $Оценка интеграла дает
(B9)
$\begin{gathered} {{I}_{2}} = \frac{1}{{{{B}^{3}}{{\beta }_{0}}}}\left[ {{{{(B + 1)}}^{3}}\ln (1 + B) - 3{{{(B + 1)}}^{2}}B + } \right. \\ \left. { + \,\,3(B + 1)\frac{{{{{(1 + B)}}^{2}} - 1}}{2} - \frac{{{{{(1 + B)}}^{3}} - 1}}{3}} \right]. \\ \end{gathered} $После дальнейшего упрощения получаем
(B10)
${{I}_{2}} = \frac{1}{{{{B}^{3}}{{\beta }_{0}}}}\left[ {{{{(B + 1)}}^{3}}\ln (1 + B) - \frac{{11}}{6}{{B}^{3}} - \frac{5}{2}{{B}^{2}} - B} \right].$Если мы хотим получить значение коэффициента трения без какого-либо приближения, следует оставить представленное выше выражение целиком. Однако, на ближайшее будущее, только лишь для получения выражения для прямой линии, примем, что B велико и оставим лишь несколько членов.
(B11)
${{I}_{2}} = \frac{1}{{{{\beta }_{0}}}}\left[ {\ln (B) - \frac{{11}}{6}} \right] = \frac{1}{{{{\beta }_{0}}}}\left[ {\ln ({{R}^{ + }}) + \ln ({{\beta }_{0}}) - \frac{{11}}{6}} \right].$Кривые, построенные по уравнениям (B10) и (В11), даны на рис. B1. Для B > 512 получается хорошая асимптота. Поскольку β0 ≈ 0.4, приближение получится хорошим при R+ > 2500.
Уравнение (В11) дает наклон прямой линии. Для сравнения с уравнением (B2), наклон равен 1/β0 = 2.708 в моем приближении для оригинального графика вихревой вязкости Никурадзе и 2.604 после моего модифицирования этого графика с целью получить обнуление на центральной линии. Для того, чтобы получить аддитивную константу, необходим первый интеграл, который мы оценим численно. Подынтегральное выражение больше не считаем сингулярным:
(B12)
$\begin{gathered} {{I}_{1}} = {{R}^{ + }}\int\limits_0^1 {\left[ {\frac{{{{\xi }^{3}}}}{{1 + {{R}^{ + }}M(\xi )}} - \frac{{{{\xi }^{3}}}}{{1 + {{\beta }_{0}}{{R}^{ + }}(1 - \xi )}}} \right]d\xi = } \\ = {{R}^{ + }}\int\limits_0^1 {\frac{{{{\beta }_{0}}{{R}^{ + }}(1 - \xi ) - {{R}^{ + }}M(\xi )}}{{[1 + {{R}^{ + }}M(\xi )][1 + {{\beta }_{0}}{{R}^{ + }}(1 - \xi )]}}{{\xi }^{3}}d\xi .} \\ \end{gathered} $Такова форма, которую следует оценить, если мы не хотим никаких приближений. Для того, чтобы получить именно константу для прямой линии, справедливую при больших значениях R+, сделаем аппроксимацию, считая R+ большой величиной:
(B13)
${{I}_{1}} = \int\limits_0^1 {\frac{{{{\beta }_{0}} - \beta (\xi )}}{{\beta (\xi ){{\beta }_{0}}(1 - \xi )}}{{\xi }^{3}}d\xi = } \int\limits_0^1 {\frac{{{{\beta }_{0}} - \beta (\xi )}}{{2\beta (\xi ){{\beta }_{0}}(1 - \xi )}}{{\xi }^{2}}d{{\xi }^{2}}.} $Выражая это, как интеграл по ξ2, получаем почти линейное подынтегральное выражение, которое теперь легко проинтегрировать численно. Для оценки I1 как приближенно, так и для получения точного уравнения, используем электронную таблицу. Аппроксимация не зависит от R+ (постольку, поскольку от R+ не зависит от M). Точный численный интеграл мы показываем в табл. B1, а полный интеграл представлен пунктиром на рис. B1.
Используя нашу оценку, запишем формулу универсального сопротивления для течения в трубе следующим образом:
(B14)
$\sqrt {{2 \mathord{\left/ {\vphantom {2 f}} \right. \kern-0em} f}} = 2.708\ln ({{R}^{ + }}) - 6.46.$Полученный наклон близок к значению, которое дал Никурадзе, но отрезок, отсекаемый на оси, сильно отличается. В связи с рис. 5 обсудим численное интегрирование уравнения (B5). Мы обнаружили (почти случайно), что следует учитывать зависимость вихревой вязкости от радиального расстояния в вязком подслое, и что это приводит к существенно отличающемуся значению отрезка, отсекаемого на оси. Наклон также может слегка меняться. Все это делает табл. B1 менее полезной.
Таблица B1.
Значения интегралов, используемых для вычисления коэффициентов трения. I1β0 составляет около 3.26 при больших R+, но нельзя игнорировать обсуждение рис. 5
| B | I2β0 | Асимпт. | I1β0 |
|---|---|---|---|
| 2 | 0.374 | –1.140 | 0.235 |
| 4 | 0.623 | –0.447 | 0.535 |
| 8 | 0.967 | 0.246 | 0.994 |
| 16 | 1.405 | 0.939 | 1.536 |
| 32 | 1.922 | 1.632 | 2.047 |
| 64 | 2.500 | 2.326 | 2.456 |
| 128 | 3.122 | 3.019 | 2.741 |
| 256 | 3.771 | 3.712 | 2.919 |
| 512 | 4.439 | 4.405 | 3.021 |
| 1024 | 5.117 | 5.098 | 3.076 |
| 2048 | 5.802 | 5.791 | 3.104 |
| 4096 | 6.490 | 6.484 | 3.119 |
| 8192 | 7.181 | 7.178 | 3.126 |
| ∞ | 3.257 |
Рисунок B1 заставляет нас предположить, что действительная кривая может показывать положительное отклонение от полученной аппроксимации, потому что она должна стремиться к нулю при малых значениях R+. Подобным же образом рис. 11 работы [2] должен был бы демонстрировать отрицательное отклонение, а на самом деле он демонстрирует положительное отклонение. Возможное объяснение этому заключается в том, что при малых R+ значение $B_{{\text{1}}}^{ + }$ уменьшается. Это наблюдается для теоремы рассеяния, но это отличается от наблюдавшейся Никурадзе независимости β0 от R+. Рисунок 5, кажется, позволяет разрешить эту проблему. Следует принимать во внимание вязкий подслой и ввести поправку в отрезок, отсекаемый на оси, используемый в законе универсального сопротивления, в сторону значения, данного Никурадзе в 1932 г.
Рис. B1.
Интеграл I2, построенный как в своей точной форме, так и в форме прямолинейной асимптоты. Точечная кривая построена для (I1 + I2) β0.
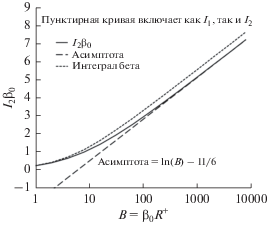
Это дает асимптотическое выражение для сопротивления. Мы никогда не видели, чтобы его когда-либо выводили таким образом, хотя Прандтль, фон Карман и Никурадзе и др. были осведомлены о результате и параметрах фитинга полного соотношения между коэффициентом трения и числом Рейнольдса из данных о скорости течения при заданном напряжении в самом широком интервале, какой только возможен.
Заметим по поводу данного упражнения, что именно значения вихревой вязкости вблизи стенки чрезвычайно важны для определения коэффициента трения. Мы увидели это, во-первых, в законе универсального сопротивления, где коэффициент при логарифмическом члене определяется главным образом наклоном кривой вихревой вязкости вблизи стенки (см. β0). Мы видим, опять-таки, что отсекаемый на оси отрезок в законе универсального сопротивления определяется главным образом вихревой вязкостью в области y3.
Список литературы
Newman, J., Theoretical analysis of turbulent mass transfer with rotating cylinders, J. Electrochem. Soc., 2016, vol. 163, p. E191.
Newman, J., Application of the dissipation theorem to turbulent flow and mass transfer in a pipe, Russ. J. Electrochem., 2017, vol. 53, p. 1061.
Nikuradse, J., Gesetzmässigkeitem der turbulentem Strömung in glatten Rohren, Forschungsheft 356, Beilage zu Forschung auf dem Gebiete des Ingenieurwesens, Edition B, Vol. 3, September/October, 1932, Berlin: VDI-Verlag, 1932. Translated as Nikuradse, J., Laws of turbulent flow in smooth pipes, NASA TT F-10, 359, Wash.: NASA, October, 1966.
Cahn, J.W. and Hilliard, J.E., Free Energy of a nonuniform system. I. Interfacial free energy, J. Chem. Phys., 1958, vol. 28, p. 258. https://doi.org/10.1063/1.1744102.
Martemianov, S.A., Statistical theory of turbulent mass transfer in electrochemical systems, Russ. J. Electrochem., 2017, vol. 53, p. 1076.
Дополнительные материалы отсутствуют.


