Электрохимия, 2019, T. 55, № 1, стр. 51-59
Турбулентное течение при вращении внутреннего цилиндраДж. Ньюмен
Дж. Ньюмен *
Калифорнийский Университет
94720-1462 Калифорния, Беркли, США
* E-mail: newman@newman.cchem.berkeley.edu
Поступила в редакцию 14.06.2018
После доработки 13.07.2018
Принята к публикации 27.08.2018
Аннотация
Диссипационная теорема дает прекрасный способ описания турбулентного массопереноса в системе с вращающимся цилиндром, хотя все же остается необходимость определения параметров путем фитинга с экспериментальными данными. К сожалению, имеющиеся экспериментальные данные содержат расхождения, которые мешают развитию теории. Настоящая работа – часть долгосрочной программы приложения предсказаний диссипационной теоремы к системам, варьирующимся от потока в трубе и вращающихся цилиндров до развитых потоков на вращающемся диске или на плоской пластинке в месте падения потока, для которых имеется широкий круг экспериментальных данных. Оказывается, что значения вихревой вязкости должны накладываться друг на друга, если разделить их на параметр напряжения R+ для того, чтобы получить когерентное поведение при очень больших числах Рейнольдса. Новый подход здесь – использовать данные по массопереносу в качестве замены при отсутствии данных о величине крутящего момента. Показано, что данные Айзенберга и Мора не составляют когерентного единства данных, несмотря на то, что они были получены на одном и том же приборе и в одной и той химической системе. Для снятия этих противоречий требуются новые экспериментальные данные. Диссипационная теорема, как предполагается, улучшит наше понимание турбулентности и позволит предсказывать ее поведение в различных системах. Следующая стадия – ее применение к развитым потокам на плоской пластинке и на вращающемся диске.
ВВЕДЕНИЕ
В работе [1] вводится понятие диссипационной теоремы и дается ее приложение к данным о массопереносе в системе вращающегося цилиндра, а именно к данным Айзенберга и данным Мора. В работе [2] эти концепции распространены на турбулентный поток в трубе. Еще больше информации о турбулентном потоке в трубе дается в работе [3]. В настоящей работе мы вновь обращаемся к системе вращающегося цилиндра, будучи обогащены опытом рассмотрения турбулентного потока в трубе. Показатель степени, используемый в расходимости, пусть остается равным 1, поскольку он подходит к цилиндрической геометрии, а не 5, как для вращающихся цилиндров или –1 для потока в трубе. Результаты для вихревой вязкости должны накладываться друг на друга для различных значений уровня напряжения (по крайней мере, при больших числах Рейнольдса), и в довершение в член затухания вводятся члены с экспонентами p и q для радиального положения и для уровня напряжения. Мы также получили информацию о том, как в вычислениях могут возникать отрицательные значения вихревой вязкости и как их можно избежать. Предполагается ввести аналогичные изменения в подход к вращающимся цилиндрам и, в особенности, получить лучшее согласие между теорией и экспериментальными данными работы [1], в которых как наклон графика зависимости числа Стантона от числа Рейнольдса, так и разброс различных значений κ, отношения внутреннего радиуса к внешнему, слишком малы.
Тонкие зазоры. Радиус Ri – это искусственный параметр для тонких зазоров; сюда относятся только толщины зазоров Ro – Ri. Поэтому (как в работе [1]) используется модифицированное число Рейнольдса ${{\operatorname{Re} }_{m}} = \kappa {{\operatorname{Re} }_{g}} = (1 - \kappa ){{\operatorname{Re} }_{i}},$ и таким образом охватывается вся область κ. По аналогичной причине используется параметр напряжения (параметр, определяющий характер протекания процесса в зависимости от механического воздействия):
(1)
$R_{m}^{ + } = {{\operatorname{Re} }_{m}}\sqrt {\frac{f}{2}} = (1 - \kappa )R_{i}^{ + } = (1 - \kappa )\frac{{{{R}_{i}}}}{\nu }\sqrt {\frac{{{{\tau }_{i}}}}{\rho }} ,$Отдельный вращающийся цилиндр. Другой экстремальный случай наблюдается, когда внешний цилиндр отстоит очень далеко от внутреннего. В работе [4] выведена формула для крутящего момента на единственном вращающемся цилиндре:
(2)
$\frac{1}{{\sqrt {{{C}_{D}}} }} = - 0.6 + 4.07\lg ({{\operatorname{Re} }_{i}}\sqrt {{{C}_{D}}} {\text{) }}.$Закон универсального сопротивления. Соотношения, связывающие коэффициент трения, вихревую вязкость, объемное рассеяние, число Рейнольдса и параметр напряжения, определены и развиты в работах [1–3]. Коэффициент трения f можно получить, интегрируя вихревую вязкость ν(t). Как показали Никурадзе [5] и его предшественники, если отложить зависимость обратной величины корня квадратного из коэффициента трения от логарифма числа Рейнольдса, помноженного на корень квадратный из коэффициента трения, то получится прямая линия. Запишем это, как
Такая форма идентична уравнению (2), но записана иначе. Этот результат, действительно, применим к большим значениям числа Рейнольдса или параметра напряжения, но Никурадзе применил его к своим экспериментальным данным, касающимся течения в трубе, вплоть до R+ = 112. Согласно работе [4], прямая линия простирается до значения $R_{i}^{ + }$ около 100. Вышеприведенная формула широко обсуждается в работе [3]. Для случая вращающихся цилиндров параметры A и B могут зависеть от отношения радиусов κ.
Исходная точка – это интеграл для системы вращающихся цилиндров,
(4)
$\begin{gathered} \sqrt {\frac{2}{f}} = R_{i}^{ + }{\text{ }}\int\limits_1^{{1 \mathord{\left/ {\vphantom {1 \kappa }} \right. \kern-0em} \kappa }} {\frac{{d\xi }}{{{{{{\xi }^{3}}(1 + {{\nu }^{{(t)}}}} \mathord{\left/ {\vphantom {{{{\xi }^{3}}(1 + {{\nu }^{{(t)}}}} \nu }} \right. \kern-0em} \nu })}}} = \\ = \frac{{R_{m}^{{\text{ + }}}}}{{1 - \kappa }}{\text{ }}\int\limits_1^{{1 \mathord{\left/ {\vphantom {1 \kappa }} \right. \kern-0em} \kappa }} {\frac{{d\xi }}{{{{\xi }^{3}}(1 + MR_{m}^{ + })}}} {\text{ }}. \\ \end{gathered} $Для течения в трубе ξ3 оказывается в числителе подынтегрального выражения вместо того, чтобы быть в его знаменателе; пределы интегрирования таковы: от ξ = 0 до ξ = 1. Величина M определена, как ${{{{\nu }^{{\left( t \right)}}}} \mathord{\left/ {\vphantom {{{{\nu }^{{\left( t \right)}}}} {\nu R_{m}^{ + }}}} \right. \kern-0em} {\nu R_{m}^{ + }}}.$ При значительном уровне турбулентности единицей в знаменателе подынтегрального выражения можно пренебречь, и коэффициент трения оказывается не зависящим от числа Рейнольдса. Однако M падает до нуля на обеих твердых стенках, и интеграл становится сингулярным. Эта трудность разрешается в формуле однородного сопротивления (3) (см. работу [3]).
Определяющие уравнения. Примем $M = {{{{\nu }^{{\left( t \right)}}}} \mathord{\left/ {\vphantom {{{{\nu }^{{\left( t \right)}}}} {\nu R_{m}^{ + }}}} \right. \kern-0em} {\nu R_{m}^{ + }}},$ $D = {{\mu {{\mathcal{D}}_{V}}} \mathord{\left/ {\vphantom {{\mu {{\mathcal{D}}_{V}}} {\tau _{i}^{{\text{2}}}}}} \right. \kern-0em} {\tau _{i}^{{\text{2}}}}},$ ξ = r/Ri, а ϕ = ln(D). В безразмерной форме соотношение между рассеянием и вихревой вязкостью для вращающихся цилиндров таково:
Предлагаемое дифференциальное уравнение, определяющее объемное рассеяние, таково:
(6)
$\frac{1}{\xi }\frac{\partial }{{\partial \xi }}\left( {\frac{1}{{{{\xi }^{3}}}}\frac{{\partial \ln D}}{{\partial \xi }}} \right) = \Lambda \frac{{{{D}^{n}}}}{{{{\xi }^{p}}{{{(R_{m}^{ + })}}^{q}}}} + \frac{{16}}{{{{\xi }^{6}}}}.$$\Lambda = {\text{Coef}}{{\left( {R_{m}^{ + }} \right)}^{{{\text{2}}n - {\text{2}}}}}$ – это безразмерная константа скорости для затухания рассеяния, ϕ = 0 при ξ = 1, ϕ = 4ln(κ) при ξ = 1/κ. Распределение полного напряжения по радиальному расстоянию r для течения в трубе можно записать, как
(7)
${{\bar {\tau }}_{{rz}}} = {{{{\tau }_{0}}r} \mathord{\left/ {\vphantom {{{{\tau }_{0}}r} R}} \right. \kern-0em} R}.$Для вращающихся цилиндров оно обратно пропорционально r2:
(8)
${{\bar {\tau }}_{{r{\theta }}}} = {{{{\tau }_{i}}R_{i}^{2}} \mathord{\left/ {\vphantom {{{{\tau }_{i}}R_{i}^{2}} {{{r}^{2}}}}} \right. \kern-0em} {{{r}^{2}}}}.$Это различие есть причина различия в определяющих уравнениях (5) и (6), а также уравнении (4). Легко показать на основе уравнения (8), что $R_{o}^{ + } = ({{{{R}_{o}}} \mathord{\left/ {\vphantom {{{{R}_{o}}} \nu }} \right. \kern-0em} \nu })\sqrt {{{{{\tau }_{o}}} \mathord{\left/ {\vphantom {{{{\tau }_{o}}} \rho }} \right. \kern-0em} \rho }} = R_{i}^{ + }$ и что поэтому его можно сократить до R+. Однако по причинам, приведенным выше, $R_{m}^{ + }$ здесь на своем месте. В работе [3] дано твердое свидетельство того, что показатель степени равняется n = 2, и предполагается, что член затухания также может содержать член, линейный по D, как в замене D n величиной D n + εD, где $\varepsilon = {{0.{\text{33}}} \mathord{\left/ {\vphantom {{0.{\text{33}}} {R_{m}^{ + }}}} \right. \kern-0em} {R_{m}^{ + }}}.$
Для ламинарного течения D = ξ2 в течении в трубе, а для вращающихся цилиндров D = 1/ξ4. Последний член в уравнении (6) добавлен для того, чтобы результат для ламинарного течения был бы решением этого уравнения, а p и q добавлены для того, чтобы обеспечить гибкость. Согласно урокам работы [2], их предпочтительные значения таковы: n = p = q = 2. Вспомним, что Λ уже содержит зависимость от $R_{m}^{ + }.$ Добавленный в уравнение (6) член, может быть, не имеет сколько-нибудь большого практического значения, в особенности для коэффициента трения при больших числах Рейнольдса.
Данные Никурадзе [5] для течения в трубе предполагают, что вихревая вязкость в потоке в трубе может быть аппроксимирована, как ν(t)/νR+ = 0.32ξ(1 – ξ). Аналогично, для вращающихся цилиндров можно предположить, что ${{{{\nu }^{{(t)}}}} \mathord{\left/ {\vphantom {{{{\nu }^{{(t)}}}} {\nu R_{m}^{ + }}}} \right. \kern-0em} {\nu R_{m}^{ + }}}\quad = C(\xi - {\text{1}})({{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\kappa - \,\,\quad\xi }}} \right. \kern-0em} {\kappa - \,\,\quad\xi }}),$ таким образом, сходя к нулю на двух твердых поверхностях. Здесь C может зависеть от κ.
Из работы [2] известно, что для течения в трубе величина p должна равняться 2(n – 1), с тем чтобы поддержать существование зависимости от r вблизи центральной линии, а величина q должна равняться 3n – 4 для того, чтобы поддержать конгруэнтность кривых вихревой вязкости, деленной на R+. Необходимо узнать, какие закономерности применимы к вращающимся цилиндрам. Ясно, что нам нужны кривые зависимости f от Re, гладкие и сохраняющие хорошее поведение при больших значениях Re и таким образом демонстрирующие предельное поведение, которое не зависит от вязкости, как это установил Никурадзе для течения в трубе. Мы видим, что основное различие между вращающимися цилиндрами и течением в трубе заключается в радиальной зависимости общего напряжения.
[До тех пор, пока мы имеем дело лишь с величиной κ, т.е. отношением радиусов, различие между $R_{i}^{ + }$ и $R_{m}^{ + }$ не существенно. Однако, данное исследование сфокусировано на определении, как турбулентность зависит от κ. В конце концов, нам нужна ясность в вопросе о том, где появляется κ, но иногда используют величину $R_{i}^{ + },$ потому что она присутствует в компьютерной программе и a priori имеет ясное определение.]
Рисунок 1 показывает, до какой стадии мы дошли в данном исследовании.
Рис. 1.
Число Стантона как функция модифицированного числа Рейнольдса, как это использовано в работе [1]. Сплошные линии представляют пять наборов экспериментальных данных Мора, длина линии представляет область охваченных чисел Рейнольдса. Пунктирные кривые вычислены по диссипационной теореме с использованием одного набора параметров: n = q = 2, p = –4, Coef = 0.01 и B+ = 0.003. Значения (1 – κ) (сверху вниз ): 0.871, 0.7487, 0.633, 0.491, 0.1723, 0.0839, 0.606, 0.0393 и 0.0172, в этом порядке, за исключением 0.1723, которому соответствует нижняя сплошная линия.

РАЗВИТИЕ
С тех пор, когда Никурадзе показал, что для течения в трубе зависимость обратной величины корня квадратного из коэффициента трения от логарифма числа Рейнольдса, помноженного на корень квадратный из коэффициента трения, выражается прямой линией, и этот метод был использован в работе [4] для представления данных по вращающему моменту для единичного вращающегося цилиндра [см. уравнение (2)], его следует также применять и к системе вращающихся цилиндров. Как Айзенберг, так и Мор не измеряли вращающий момент в системе вращающихся цилиндров и не дали значений коэффициента трения. Однако, в пределе больших чисел Шмидта число Стантона связано с коэффициентом трения следующим уравнением:
(9)
${\text{StS}}{{{\text{c}}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} = \left[ {{{{{{\left( {{{B}^{ + }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \mathord{\left/ {\vphantom {{{{{\left( {{{B}^{ + }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} {1.2092}}} \right. \kern-0em} {1.2092}}} \right]{{\left( {{f \mathord{\left/ {\vphantom {f 2}} \right. \kern-0em} 2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$Это означает, что прямая линия получится, если отложить 1/StSc2/3 против логарифма числа Рейнольдса Rem, помноженного на StSc2/3. Это продемонстрировано на примере оригинальных экспериментальных данных на рис. 2.
Рис. 2.
Экспериментальные данные Айзенберга (от a до e) и Мора (от ж до и), представленные в форме графика 1/StSc2/3 = a + b ln(RemStSc2/3); наилучшие параметры фитинга даны в табл. 1 вместе со значениями Coef и B+, которые дают наилучшее согласие для индивидуальных значений κ.

Рис. 2.
Окончание.

Существует естественное предположение, что коэффициент турбулентной диффузии равен турбулентной кинематической вязкости, D(t) = ν(t). Теоретические результаты, имеющиеся в литературе, говорят о том, что это предположение может выполняться лишь приближенно. В лучшем случае одна величина может быть пропорциональна другой, но даже их отношение может меняться с положением в пространстве. Редко удается найти данные для этих двух величин, измеренные одновременно. При больших числах Шмидта выражение, подобное уравнению (9), можно использовать для того, чтобы сделать вывод о величине коэффициента турбулентной диффузии. Этими соображениями можно объяснить наблюдение, сделанное ниже в настоящей работе, о том, что значение B+, найденное из измерений массопереноса, существенно отличается от полученного из измерений вращающего момента (см. раздел “Расхождения”).
Значения наименьших квадратов наклонов этих кривых и отрезков, отсекаемых ими на оси, b и a, даны в табл. 1 вместе с характеристикой качества фитинга σ и значениями Coef и B+, использованными при расчете близких аппроксимаций прямых на рис. 2 на основе диссипационной теоремы. Дополнительный член в уравнении (6) сохранен, хотя бы он и не имел какого-либо значения. Область чисел Рейнольдса, охваченная в этих экспериментах, в действительности не очень широка. Никурадзе приложил много усилий для того, чтобы довести число Рейнольдса в своих экспериментах с течениями в трубе до 3 × 106, с тем чтобы исследовать их поведение при действительно больших числах Рейнольдса. В данных, представленных рис. 2, не видно явных искривлений, за исключением может быть одного при 1 ‒ κ = 0.871.
Таблица 1.
Значения параметров для рис. 2; (1 – κ) – размер зазора, a – отрезок, отсекаемый кривыми на оси, b – наклон фитинга 1/StSc2/3 = a + b ln(RemStSc2/3), σ – характеристика качества фитинга, а Coef и B+ – параметры, использованные в компьютерной программе на основе диссипационной теоремы. Эта таблица есть дополнение к табл. I в работе [1]; в обеих таблицах используются одни и те же экспериментальные данные, но их фитинг проведен разными способами
| 1 – κ | a | b | σ | Coef | B+ |
|---|---|---|---|---|---|
| 0.8710 | –88.7 | 49.6 | 0.0920 | 0.030 | 0.004 |
| 0.7487 | –184.5 | 83.9 | 0.0256 | 0.010 | 0.007 |
| 0.6330 | –261.4 | 109.0 | 0.0010 | 0.007 | 0.0085 |
| 0.4910 | –179.8 | 107.4 | 0.0485 | 0.007 | 0.008 |
| 0.1723 | –307.9 | 203.7 | 0.0561 | 0.003 | 0.009 |
| 0.0839 | –122.4 | 100.0 | 0.0140 | 0.012 | 0.0125 |
| 0.0606 | –141.5 | 124.6 | 0.0027 | 0.008 | 0.011 |
| 0.0393 | –70.7 | 126.5 | 0.0079 | 0.010 | 0.0059 |
| 0.0172 | –106.2 | 193.8 | 0.0184 | 0.0065 | 0.0032 |
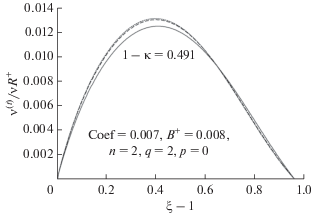
На рис. 3 показаны профили вихревой вязкости, вычисленные с помощью диссипационной теоремы. Видно, что они накладываются друг на друга при больших значениях $R_{i}^{ + },$ а при меньших значениях они сдвигаются вниз. Напротив, экспериментальные данные Никурадзе для более низких значений R+ ложатся выше предельной кривой при больших R+ для течений в трубе.
Рис. 3.
Профили ${{{{\nu }^{{(t)}}}} \mathord{\left/ {\vphantom {{{{\nu }^{{(t)}}}} {\nu R_{i}^{{\text{ + }}}}}} \right. \kern-0em} {\nu R_{i}^{{\text{ + }}}}}$ как функция (ξ – 1) для нескольких значений $R_{i}^{ + }$ и для (1 – κ ) = 0.491. Верхняя точечная кривая: $R_{i}^{ + }$ = 16399, пунктирная кривая: $R_{i}^{ + }$ = 3049, сплошная кривая: $R_{i}^{ + }$ = 567.
На рис. 4 показаны профили объемного рассеяния, умноженного на ξ4 для того, чтобы привести их к единице на внешнем цилиндре. Логарифмическая шкала показывает, что кривые похожи друг на друга по форме, за исключением области вблизи цилиндра, где установлены граничные условия. Таким образом, в общем случае рассеяние обратно пропорционально R+. Как установлено в работе [1], в турбулентном потоке рассеяние наблюдается главным образом вблизи внутреннего цилиндра, как в течении в трубе. Другими словами, рассеяние устанавливается на стенках, но вращающий момент велик, если при этих больших числах Рейнольдса может превалировать ламинарное распределение.
Рис. 4.
Значения D, помноженные на ξ4 для того, чтобы привести их вновь к единице на внешнем цилиндре.
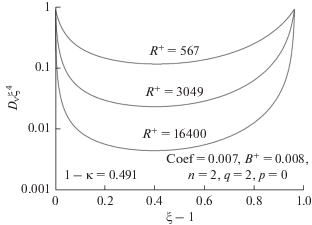
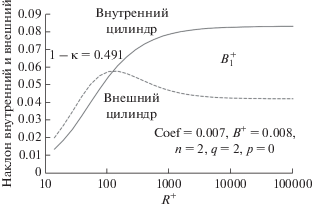
Рисунок 5 показывает вычисленный параметр $B_{{\text{1}}}^{ + }$ на внутреннем и внешнем цилиндрах. Это наклон профилей вихревой вязкости на твердой стенке, если не принимать в расчет вязкий подслой. Как и в работе [1], кривые поднимаются с ростом уровня напряжения, а затем выравниваются. В отличие от работы [1], здесь эти значения остаются на том же уровне даже при больших значениях R+. Это имеет отношение к наложению профилей вихревой вязкости, измеренных Никурадзе для течений в трубе. Таково одно из усовершенствований по сравнению с течением в трубе, необходимое для вращающихся цилиндров.
Рис. 5.
Наклоны профилей вихревой вязкости вблизи стенки, но за пределами вязкого подслоя. Очевидно, что они должны расти от нуля и выходить на плато. В работе [1] они начинают вновь расти справа, что может быть связано с плохим коэффициентом трения при больших числах Рейнольдса. Этого можно избежать с помощью наложения профилей вихревой вязкости друг на друга.
На рис. 6 показан наилучший фитинг для всех значений отношения радиусов κ, с параметрами Coef и B+, подобранными для каждого отношения и приведенных в табл. 1. Он аналогичен показанному на рис. 1, но здесь график построен согласно формуле универсального сопротивления, а не в билогарифмической системе.
Рис. 6.
Сравнение результатов, полученных для диссипационной теоремы и массопереноса. Для получения хорошего согласия (в частности, справа) были использованы два подгоночных параметра. Кривые загибаются слева с тем, чтобы избежать отрицательных значений. Невозможно добиться согласия при всех значениях κ, имея только одно значение Coef и одно значение B+. Данные Мора представлены точечными линиями, а данные Айзенберга – сплошными.

Остальные рисунки (не показанные здесь) дают некоторую идею насчет того, чтó можно получить, меняя параметры, но поддерживая их единообразными при всех значениях κ. Это не дало удовлетворительного согласия для всех кривых, но это также не дало сколько-нибудь значительного дополнительного проникновения в суть проблемы. Рисунок 7 предлагает хороший компромисс для параметров, но держит их единообразными при всех значениях κ. Разброс для всех значений κ почти правильный, и кривые для всех зазоров (данные Айзенберга, согласно которым (1 – κ) превышает 0.17) пересекают экспериментальные кривые, даже если они имеют отличающийся наклон. Однако, разброс кривых для узких зазоров (данные Мора) сильно отличается от экспериментальных кривых, и они даже накладываются на них при (1 – κ) = 0.1723. При увеличении Coef наклон рассчитанных кривых, в общем, уменьшается, в то время как увеличение B+ снижает всю кривую. Значения Coef и B+, использованные здесь, существенно отличаются от ожидаемых на основании проанализированных нами данных по вращающему моменту (см. Приложение A ).
Рис. 7.
Наилучший фитинг, достижимый с одним только значением каждого параметра. Хороший наклон получается при (1 – κ) = 0.871, но он становится слишком низким для более тонких зазоров. Разброс относительно нормальный, но расстояние между точками не согласуется с данными. Для того, чтобы получить разброс данных Мора, могут понадобиться отдельные значения B+ для каждой ширины зазора, см. табл. 1. Расстояние между точками для данных Айзенберга относительно неплохое, но основная слабость обоих наборов данных – плохое их перекрывание. Значения Coef и B+ отличаются от тех, что получены из данных по коэффициенту трения, см. Приложение A . Для каждого значения κ число Стантона следует умножить на такой множитель, который сдвигает точку пересечения с пунктирной кривой к полусумме крайних значений. Результаты, полученные после умножения на этот фактор, показаны точечными прямыми. Для того, чтобы оказаться в середине пунктирных кривых, были использованы такие множители: 0.94, 1.07, 1.07, 1.07, 0.98, 0.52, 0.63, 0.7 и 1.12 (от 0.871 до 0.0172).

Становится ясно, что данные и Айзенберга, и Мора не составляют единого, самосогласованного набора данных. Это особенно ясно видно, если приложить к этим данным некоторый эмпирицизм. Из табл. I работы [1] следует, что степеннáя зависимость числа Стантона от числа Шмидта имеет показатель степени около –2/3; он отличается от теоретического значения всего лишь на ~0.01, что в некотором смысле понятно из известной зависимости от числа Шмидта для случая ламинарного течения. Рисунок 1 в настоящей работе и табл. I работы [1] показывают, что эти кривые имеют одинаковые наклоны для зависимости от числа Рейнольдса, меняясь случайным образом, приблизительно на –0.3. Поэтому для получения зависимости числа Стантона от отношения зазоров, рассчитанной для каждой экспериментальной точки (всего 134 точки), следует отложить ${\text{StS}}{{{\text{c}}}^{{{{\text{2}} \mathord{\left/ {\vphantom {{\text{2}} {\text{3}}}} \right. \kern-0em} {\text{3}}}}}}{\text{Re}}_{m}^{{0.{\text{3}}}},$ как функцию (1 – κ), как это сделано на рис. 8.
Рис. 8.
Данные Айзенберга и данные Мора, отложенные как функция ширины зазора с тем, чтобы показать, что эти два набора данных сильно различаются. Приведены все данные, включая и выпадающую точку при (1 – κ) = 0.633, показанную также на рис. 2в. Показаны также предсказания диссипационной теоремы, с использованием тех же результатов, что и на рис. 7.
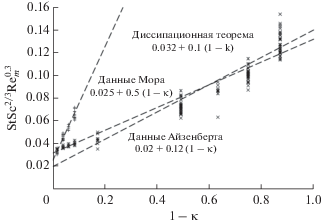
Показатель степени, который следует использовать при числе Рейнольдса, вероятно, постепенно слегка изменяется с размером зазора (1 – κ), но табл. I работы [1] показывает, что наилучший показатель степени, который следует использовать, существенно изменяется с (1 – κ), так что нелегко определить, какова величина этого “слегка”. Результирующая величина, отложенная на рис. 8, должна поэтому наиболее сильно зависеть от самой величины (1 – κ). Графики весьма информативны; разброс для каждого конкретного значения (1 – κ) связан частично с разностью между показателем степени 0.3, использованным для Rem, и более подходящим его значением, данным в табл. I работы [1], а частично – с тем фактом, что предсказания диссипационной теоремы дают наклон, меняющийся с числом Рейнольдса (см. рис. 7). Однако, здесь видны две существенно различных тенденции: одна – для данных Мора (небольшие значения (1 – κ)), а вторая – для данных Айзенберга.
[Это различие между двумя наборами данных существует уже 3 года. Его можно представить различными способами, такими, например, как графики зависимости StSc2/3Re или NuSc2/3 от Rei. Эта информация лучше видна из рис. 8. Другой способ представить это различие – график ординаты на рис. 8, деленной на (1 – κ)0.3(1.25 – κ), как функция Rem. Здесь получаются две отдельных горизонтальных линии, но опять-таки рис. 8 показывает это яснее и нагляднее.]
РАСХОЖДЕНИЯ
По мере развития работы над диссипационной теоремой существенно уменьшилось появление заметных расхождений. Одно из остающихся – то, что данные Айзенберга и данные Мора не гармонируют друг с другом, и это вносит неуверенность в интерпретацию. Получаются не самосогласованные параметры. Другое расхождение заключается в том, что одни и те же параметры, полезные при расчетах трения, не согласуются с параметрами, используемыми при интерпретации результатов по массопереносу. Причиной этого последнего расхождения может быть “врожденное” различие между коэффициентом турбулентной диффузии и турбулентной кинематической вязкостью, как показывает уравнение (9).
ЗАКЛЮЧЕНИЕ
Для подтверждения или опровержения выводов развиваемой в данной работе теории были бы полезны дополнительные тщательные эксперименты в обеих областях – трения и массопереноса. Тогда, возможно, в эту теорию можно будет внести подходящие уточнения. Величины вихревой вязкости, деленные на R+, должны накладываться друг на друга, если стремиться к согласованному поведению при очень больших числах Рейнольдса.
ПРИЛОЖЕНИЕ A . СФОКУСИРУЕМСЯ НА ТРЕНИИ
Используем диссипационную теорему для фитинга результатов работы [4] по вращающему моменту для одиночных цилиндров [см. уравнение (2)]. Здесь мы используем диссипационную теорему для предсказания коэффициента трения при значениях κ в области вплоть до 1, т.е. в пределе тонкого зазора. Результаты показаны на рис. A1.
Рис. A1.
Рассчитанные коэффициенты трения для вращающихся цилиндров. Значение Coef положено равным 0.17 для того, чтобы получить согласие с экспериментальными данными работы [4] для κ = 0 (сплошная линия). Затем были вычислены кривые для многих значений (1 – κ). Широкие зазоры при (1 – κ) > 0.2 демонстрируют медленный рост, приводя в конце концов к более крутым наклонам. Такое поведение представляет интерес для получения большей ясности в поведении узких зазоров. График зависимости от Rem(f/2)0.5 прекрасно демонстрирует предел как для малых, так и для больших значений (1 – κ), причем линии не пересекаются. При B+ = 0.02 (пунктирные кривые) вязкий подслой не оказывает существенного влияния, и получаются, в основном, прямые линии. Светлые пунктирные линии добавлены для того, чтобы показать влияние изменения B+ от 0.02 до 0.0005. (Для этих кривых значения (1 – κ) такие же, что и для B+ = 0.02, и имеют тот же порядок величины.) Ордината увеличивается до существенно более высоких значений (более низкое трение), сравн. рис. 5 работы [3].

Наклоны демонстрируют постоянное продвижение вперед по мере утоньшения зазора. Данные Айзенберга могут не подтверждать то, что ожидается для тонких зазоров, потому что, в действительности, они получены для толстых зазоров. Рисунок A1 содержит предсказание коэффициента трения для очень тонких зазоров, основываясь на данных для очень широкого зазора.
Полезно было бы исследовать, что произойдет, если значение p меняется от 0 до 2, или –4, или –2, потому что это – степень свободы при фитинге экспериментальных данных. Изменение p до –4 увеличивает разброс кривых для различных значений κ; величина p оказывает пренебрежимо малое влияние при тонких зазорах и может быть не слишком важной при толстых зазорах.
В работе [6] приводятся данные по коэффициенту трения для вращающихся цилиндров. Это должно стать важным дополнением для нашей продолжающейся работы по массопереносу в этой системе. На рис. A2 показаны данные для трех различных по ширине зазоров.
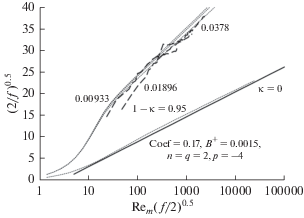
Рис. A2.
Данные из работы [6] по коэффициенту трения для течения в воздухе для системы с внутренним цилиндром (с радиусом 6.0025 дюйма), вращающимся при ширине зазора (1 – κ), равной 0.00933, 0.01896 и 0.0378; график построен по типу закона универсального сопротивления. Модифицированное число Рейнольдса равно Rem = κReg, где Reg – это число Рейнольдса, основанное на ширине зазора. Для перспективы результаты дополнены взятыми из работы [4] данными для трения с единичным цилиндром в большом контейнере (κ = 0). Показаны также результаты для диссипационной теоремы с параметрами, приведенными на этом рисунке. Рассчитанные кривые для каждого из отношений зазоров также добавляют перспективы. Кривые для узких зазоров лежат выше кривых для широких зазоров.
Даже после исследования этой системы в течение 2 или 3 лет у меня сложилось весьма смутное представление о том, где должны лежать новые результаты. Мы пришли к заключению о том, что наилучшее значение n – это 2, а для систем с трубой q и p должны тоже равняться 2. Для этой системы p может быть –4; это заключение основано на некоторой догадке о связи с распределением напряжений в этой системе.
Два еще более важных параметра – это Coef и B+. Первый из них – это коэффициент для члена затухания–рассеяния, а второй относится к вязкому подслою в непосредственной близости от твердой стенки. График на рис. A1, охватывающий полный спектр значений κ, оказывается весьма полезным, так как он дает гораздо более твердую идею использовать релевантные значения при попытках скоррелировать данные Айзенберга и данные Мора по массопереносу с диссипационной теоремой.
Список литературы
Newman, J., Theoretical Analysis of Turbulent Mass Transfer with Rotating Cylinders, J. Electrochem. Soc., 2016, vol. 163, p. E191.
Newman, J., Application of the Dissipation Theorem to Turbulent Flow and Mass Transfer in a Pipe, Russ. J. Electrochem., 2017, vol. 53, p. 1061.
Ньюмен, Дж. Развитие представлений о турбулентном течении в трубе. Электрохимия. 2019 (принято к печати). [Newman, J., Further Thoughts on Turbulent Flow in a Pipe, Russ. J. Electrochem., 2019 (in press).
Theodorsen, T. and Regier, M., Experiments on Drag of Revolving Disks, Cylinders, and Streamline Rods at High Speeds, National Advisory Committee for Aeronautics, Report № 793, 1944.
Nikuradse, J., Gesetzmässigkeitem der turbulentem Strömung in glatten Rohren, Forschungsheft 356, Beilage zu Forschung auf dem Gebiete des Ingenieurwesens, Edition B, vol. 3, September/October, 1932 (Berlin: VDI-Verlag GMBH, 1932). Translated as J. Nikuradse, “Laws of Turbulent Flow in Smooth Pipes,” NASA TT F-10, 359 (Washington: National Aeronautics and Space Administration, October, 1966).
Gorland, S.H., Kempke, E.E., Jr., and Lurnannick, S., Experimental Windage Losses for Close Clearance Rotating Cylinders in the Turbulent Flow Regime, Cleveland, OH: Lewis Research Center, June, 1970. NASA Technical Memorandum, NASA TM X-52851.
Дополнительные материалы отсутствуют.


