Электрохимия, 2020, T. 56, № 10, стр. 880-895
Новые перспективы в исследовании турбулентности
Дж. Ньюмен *
Калифорнийский Университет
94720-1462 Калифорния, Беркли, США
* E-mail: newman@newman.cchem.berkeley.edu
Поступила в редакцию 28.09.2019
После доработки 06.11.2019
Принята к публикации 20.02.2020
Аннотация
Обсуждаются недавно выполненные исследования применения диссипативной теоремы к турбулентному течению на примере вращающихся цилиндров, потока в трубе и потока вдоль плоской пластинки при нулевом угле набегания. Рассчитанные зависимости вихревой вязкости и вихревого коэффициента диффузии от расстояния до твердой стенки подтверждены математической обработкой флуктуаций. Обсуждается роль вязкого подслоя в гидродинамическом трении.
ВВЕДЕНИЕ
В период между 1940 г. и, приблизительно, 1980 г. в научной литературе СССР вновь появились многочисленные публикации о режиме турбулентности. Кажется вполне уместным, что специальный выпуск журнала “Электрохимия”, посвященный столетию со дня рождения В.С. Багоцкого, включает обсуждение турбулентности, представляющей для электрохимиков большой интерес. Электрохимические системы очень подходят для изучения турбулентности и для того, чтобы продемонстрировать ее влияние на поведение систем.
Внимание электрохимиков обычно сфокусировано на поверхности электрода и на происходящих на ней реакциях. Осложняющим обстоятельством являются ограничения, связанные с массопереносом; их следует учитывать при корректной интерпретации химических явлений. Но турбулентность – это сложное явление, которое требует больших усилий от электрохимиков для того, чтобы его объяснить и создать надежную предсказательную теорию. Настоящую работу мы начнем с попытки понять весьма ценные данные по массопереносу в электрохимической системе, состоящей из внешнего стационарного цилиндрического электрода и внутреннего вращающегося такого же электрода. Были потрачены значительные усилия для того, чтобы показать, как результаты зависят от величины κ – отношения радиусов внутреннего цилиндра к внешнему, и разработать диссипативную теорему в приложении к турбулентному течению.
Теория пытается найти локальные законы, управляющие соотношениями между различными усредненными статистическими характеристиками турбулентности, прежде всего между вихревой вязкостью и объемным рассеянием. Это дает некоторое представление о системе вращающихся цилиндров. Еще больший прогресс достигается при приложении теории к стационарному полностью развившемуся течению в круглой трубе. В статье Никурадзе [1] (1932 г.) описан широкий круг измерений профилей скорости, коэффициентов трения и значений вихревой вязкости для чисел Рейнольдса от 4000 до 3 200 000. Диссипативная теорема объясняет полученные результаты, а также позволяет извлечь из этих ранних, но тщательно выполненных исследований много полезной информации.
Диссипативная теорема также применима к развивающемуся потоку вдоль плоской пластинки при нулевом угле набегания, когда поток является ламинарным (и хорошо описывается) вблизи передней кромки, а затем подвергается турбулизации и в конце концов превращается в полностью развитый турбулентный поток, подобный тому, который Никурадзе наблюдал для потока в трубе при изменении числа Рейнольдса.
Вращающийся диск – удобная экспериментальная система, широко используемая в электрохимических исследованиях. Течение жидкости в этой системе также хорошо исследовано, оно носит ламинарный характер вблизи оси вращения, далее к периферии диска следует переходная область, и в конце концов во внешней области наступает хорошо выраженная турбулентность. Это очень похоже на то, что наблюдается в различных областях системы “плоская пластинка” по мере того, как поток движется вдоль ее поверхности.
Остается выяснить, насколько хорошо соблюдается диссипативная теорема при пристальном изучении.
В параллельном исследовании Колмогоров [2] разработал теорию затухания турбулентности в системе, в которой среда почти однородна и изотропна. Это должно иметь отношение к затуханию рассеяния и в других геометриях.
В независимых, но идейно связанных исследованиях [3–5] выяснилось, что в турбулентном потоке с поперечным градиентом скорости существует область, расположенная очень близко к твердой стенке, в которой степень турбулизации постепенно уменьшается по мере приближения к стенке. Эту область называют вязким подслоем. Поскольку она располагается очень близко к поверхности, то предпочтительно исследовать ее с помощью массопереноса электролита при высоких числах Шмидта (число Шмидта Sc = ν/$\mathcal{D}$ – это отношение кинематической вязкости к коэффициенту диффузии).
Неожиданный результат приложения диссипативной теоремы к турбулентности заключается в том, что в этом слое существует очень сильное трение, причем значительную долю полного трения составляет трение в вязком подслое. Это было продемонстрировано данными 1932 г. по течению в трубе, причем Никурадзе [1] мог и не осознавать, что измеренные им коэффициенты трения не находятся в согласии с измеренными вихревыми коэффициентами диффузии.
Этот вязкий подслой настолько тонок, а турбулентность падает так быстро, что турбулентные вихри оказываются независимыми друг от друга. Это позволяет использовать преобразование Фурье для объяснения профиля вихревой вязкости, а также вихревых коэффициентов диффузии в непосредственной близости от стенки.
В настоящей работе дан обзор различных аспектов турбулентности.
ДИССИПАТИВНАЯ ТЕОРЕМА
Ньютон постулировал, что в движущейся текучей среде напряжение должно быть локально связано с пространственной производной от скорости; коэффициент пропорциональности называется вязкостью μ. Турбулентное течение сложнее; оно характеризуется быстрыми и, как кажется, случайными флуктуациями скорости и давления. Оно должно описываться локальными соотношениями между некоторыми статистическими усредненными величинами, касающимися движения текучей среды. Эти статистические величины могут включать, главным образом, вихревую вязкость и объемное рассеяние, но также и напряжение в текучей среде и плотность энергии турбулентных вихрей. Напряжение Рейнольдса – это плотность потока импульса или напряжение, т.е. плотность, умноженная на усредненные две флуктуирующие компоненты скорости.
Вихревая кинематическая вязкость ν(t) определена, как коэффициент между средним напряжением и пространственной производной от средней скорости, что очень похоже на соотношение Ньютона для ламинарного потока.
(1)
$ - \tau = {{\bar {\tau }}_{{xy}}} = - \rho (\nu + {{\nu }^{{(t)}}})\frac{{\partial {{{\bar {v}}}_{x}}}}{{\partial y}}.$Поскольку обе величины – напряжение и пространственная производная – это тензоры, то вихревая кинематическая вязкость – это тоже тензор с 81 компонентами, но во многих простых геометриях нас обычно интересует скалярная форма этого уравнения. Поэтому со знаком минус τ может стать положительной величиной. Объемное рассеяние – это бискалярное произведение напряжения и производной от скорости. В турбулентном потоке рассеяние связано с напряжением и полной скоростью приближенным соотношением:
(2)
${{\mathcal{D}}_{V}} = - \tau :\nabla {\mathbf{v}} \approx \frac{{{{\tau }^{2}}}}{{\rho (\nu + {{\nu }^{{(t)}}})}}.$Чтобы получить достаточно уравнений для того, чтобы соответствовать числу неизвестных величин, необходимо постулировать, каким образом объемное рассеяние ${{\mathcal{D}}_{V}}$ меняется во времени и пространстве под влиянием конвекции, диффузии и затухания. Вот компонентный состав диссипативной теоремы:
(3)
$\frac{{\partial {{\mathcal{D}}_{V}}}}{{\partial t}} + {\mathbf{\bar {v}}} \cdot \nabla {{\mathcal{D}}_{V}} = \nabla \cdot \left[ {(\nu + {{\nu }^{{(t)}}})\nabla {{\mathcal{D}}_{V}}} \right] - \frac{{k{{{({{\mathcal{D}}_{V}})}}^{n}}}}{{{{\xi }^{p}}{{{({{R}^{ + }})}}^{q}}}}.$В первых примерах применения тензорная природа вихревой кинематической вязкости не учитывалась. Члены в левой части уравнения описывают изменения рассеяния во времени под влиянием конвекции. Первый член в правой части уравнения отвечает предположению, что полная кинематическая вязкость играет роль диффузии в рассеянии. Последний (размерный) член – это затухание рассеяния, он описывает, каким образом рассеяние затухает, будучи предоставлено самому себе. Предполагается, что рассеяние затухает с постоянной времени k по закону второй степени объемного рассеяния (n = 2), хотя при малых значениях рассеяния можно добавлять член первого порядка.
Для того чтобы установить форму члена, описывающего затухание, необходимо некоторое эмпирическое доказательство. Исследование турбулентного потока в трубе [1] сыграло важную роль в описании этого затухания. Необходимо также использовать теорию однородной изотропной турбулентности. К счастью, здесь проявляются некоторые общности, так что появляется возможность предсказывать турбулентное течение в различных геометриях и обстоятельствах. Полезными являются множители, относящиеся к напряжению и числу Рейнольдса в степенях p и q из уравнений для потока в трубе.
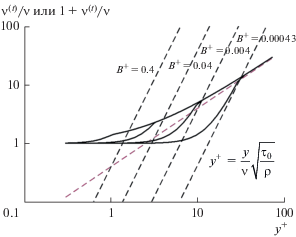
Рисунок 1 помогает читателю понять, каким образом различные факторы влияют на вихревую и полную вязкость. Кинематическая вязкость присутствует всегда и доминирует вблизи твердой стенки. Вихревая вязкость убывает вблизи твердой стенки – по линейному закону в той области, где доминирует турбулентное течение, но по закону y3 в вязком подслое. В настоящей работе такое поведение будет продемонстрировано на многих примерах.
Рис. 1.
Зависимость вихревой вязкости от расстояния. Напряжение у стенки τ0 – это обычный способ вывести универсальный профиль вблизи стенки, используя координату y+. Три прямых (на билогарифмическом графике) – это компоненты полной вязкости. Первая компонента – это собственно кинематическая вязкость, которая здесь изображена горизонтальной прямой со значением 1. В вязком подслое вихревая вязкость может быть представлена наклоном 3, как в соотношении ν(t)/ν = B+(y+)3. Сразу вне вязкого подслоя наклон становится равным 1, как в соотношении ν(t)/ν = $B_{{\text{1}}}^{ + }{{y}^{ + }}.$ Их следует должным образом добавить, с тем чтобы получить полную вязкость, выбирая для вихревой кинематической вязкости наименьшее из двух. Коэффициенты B+ и $B_{{\text{1}}}^{ + }$ следует соотнести друг с другом. Снаружи пограничного слоя диссипативная теорема может показать, каким образом ν(t)/ν зависит от расстояния от стенки. На рисунке показано только одно значение $B_{{\text{1}}}^{ + }$ и четыре значения B+.
Первые два примера, а именно концентрические цилиндры и течение в трубе, – это геометрии, в которых распределение напряжения можно заранее предсказать. Соответственно, часто удобнее использовать параметр напряжения R+ = = (R/ν)(τ0/ρ)0.5 для трубы и аналогичный параметр $R_{i}^{ + }$ на основе внутреннего радиуса вращающегося цилиндра. Следующие два примера – это развивающиеся течения, одно на плоской пластинке при нулевом угле набегания, другое – на вращающемся диске. В обеих этих системах течение ламинарное вблизи точки, от которой оно начинает двигаться вдоль твердой стенки, далее следует переход к турбулентности, и в конце концов наступает хорошо выраженное турбулентное течение, при котором кинематическая вязкость уже не играет определяющей роли. Здесь имеется аналогия с первыми двумя типами течений, прогрессирующая с ростом параметра напряжения. Однако, недостаток информации о распределении напряжения требует, чтобы уравнение сохранения количества движения и уравнение непрерывности решались одновременно с уравнениями рассеяния.
ВРАЩАЮЩИЕСЯ ЦИЛИНДРЫ
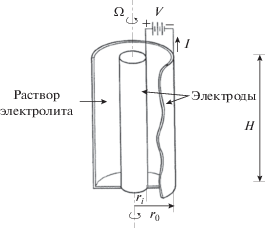
Фундаментальные исследования турбулентного массопереноса [6] были выполнены в электрохимической системе, в которой внутренний вращающийся цилиндр обеспечивает интенсивное перемешивание и делает поток турбулентным. Такая система является идеальной для электрохимических исследований, поскольку она относительно компактна, имеет равномерное распределение плотности тока и может достигать высоких скоростей массопереноса. Ее использовали в нескольких исследованиях коррозии. Она также будет особенно полезна в исследованиях турбулентности. В статье [6] изучались пять различных значений κ; они не были использованы должным образом, но это будет сделано в настоящей работе. В работе [7] эти значения κ были применены к значительно более тонким зазорам. Распределение напряжения в радиальном направлении легко вычислить, хотя об экспериментальных измерениях полного напряжения или крутящего момента не сообщалось. Тот факт, что крутящий момент легко измерим и непосредственно связан с полным рассеянием в потоке, также служит мотивацией к исследованию этой системы в турбулентном потоке и для выбора объемного рассеяния в качестве полезной статистической величины. Геометрия этой системы представлена на рис. 2.
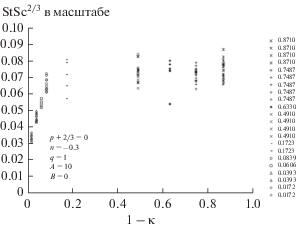
На рис. 3 приведены экспериментальные данные [6, 7] в виде числа Стентона St, умноженного на число Шмидта в степени 2/3. В работе [6] использовано число Рейнольдса, вычисленное на основе радиуса внутреннего цилиндра:
Рис. 3.
Зависимость числа Стентона St от модифицированного числа Рейнольдса для массопереноса к внутреннему вращающемуся цилиндру. Пять наборов экспериментальных данных [6] имеют следующие значения величины 1 – κ: 0.871, 0.7487, 0.633, 0.491 и 0.1723. Четыре набора экспериментальных данных [7] относятся к более тонким зазорам и имеют следующие значения 1 – κ: 0.0839, 0.0606, 0.0393 и 0.0172. Пунктирные линии вычислены на основе диссипативной теоремы с использованием параметров, приведенных на рисунке. Обозначения – как на рис. 4.
Но для ячеек с тонким зазором больше подходит использование числа Рейнольдса, вычисленного на основе толщины зазора:
Поэтому мы предпочитаем пользоваться таким модифицированным числом Рейнольдса:
(6)
${{\operatorname{Re} }_{{\text{m}}}} = (1 - \kappa ){{\operatorname{Re} }_{i}} = \kappa {{\operatorname{Re} }_{{\text{g}}}},$Те же данные приведены на рис. 4, из которого яснее видно, насколько экспериментальные данные расходятся с теорией.
Рис. 4.
Данные по массопереносу к внутреннему вращающемуся цилиндру для различных отношений κ радиусов внутреннего и внешнего цилиндров. При уменьшении толщины зазора предсказания на основе диссипативной теоремы постепенно снижаются. Данные [7] для тонких зазоров не согласуются с данными для более толстых зазоров.
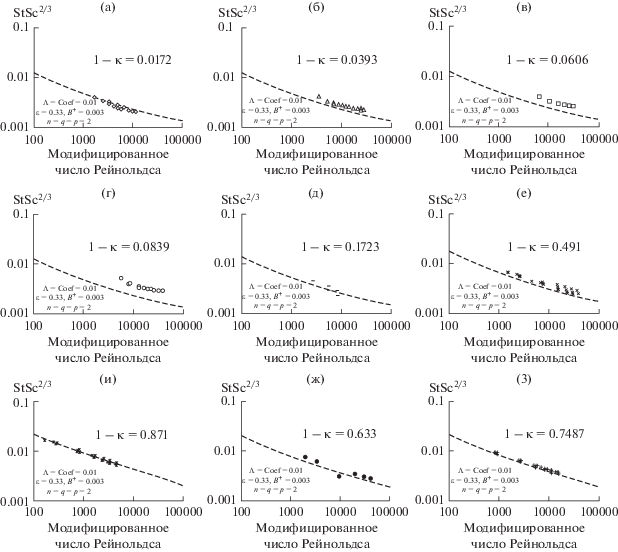
Эти данные хорошо описываются эмпирической формулой:
(7)
${\text{StS}}{{{\text{c}}}^{{2/3}}} = A\operatorname{Re} _{{\text{m}}}^{n}{\text{S}}{{{\text{c}}}^{p}}.$Для различных значений κ качество фитинга колеблется от 0.03 до 0.13. Показатель степени n меняется от –0.46 до –0.28 без какого-либо строгого правила; это изменение n отражается в величине A. Однако, показатель степени p+ 2/3 для числа Шмидта очень близок к –0.01, и поэтому он весьма близок к теоретической величине для ламинарного массопереноса при высоких значениях Sc. Этот показатель степени также весьма близок к теоретической величине для турбулентного массопереноса, когда вихревая вязкость пропорциональна y3 в вязком подслое. (См. раздел о вязком подслое.) Напротив, в работе [6] не принимаются в расчет различные значения κ, для которых взяты точные данные; приводится фитинг для всех данных из статьи, согласно соотношению
(8)
${\text{StS}}{{{\text{c}}}^{{2/3}}} = 0.0642\operatorname{Re} _{i}^{{ - 0.3}}{\text{S}}{{{\text{c}}}^{{0.0227}}}.$Таким образом, знак показателя степени при Sc противоположен тому, который использован для фитинга при каждом значении κ. Ни одно значение κ не имеет показателя степени, приближающегося к 0.0227; все они ближе к –0.01.
На рис. 3 и 4 диссипативная теорема представлена пунктирными линиями [8, 9]. Для всех значений κ использован один и тот же набор параметров. На рис. 5 и 6 показаны предсказанные профили вихревой вязкости и объемного рассеяния для 1 – κ = 0.491. Здесь ξ = r/ri, а рассеяние приводится в безразмерном виде; для внутреннего цилиндра его значение таково:
где τi – напряжение около внутреннего цилиндра. Величина D умножена на ξ4, так что на внешнем цилиндре откладываемая величина равняется 1.Рис. 5.
Профили ν(t)/ν$B_{{\text{1}}}^{ + }$ в зависимости от ξ – 1 для нескольких значений $R_{i}^{ + }$ и для 1 – κ = 0.491. Верхняя кривая с короткими штрихами имеет Ri+ = 16399, кривая с длинными штрихам – $R_{i}^{ + }$ = 3049, а сплошная линия – $R_{i}^{ + }$ = 567.
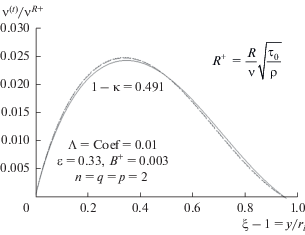
Рис. 6.
Значения D, умноженные на ξ4 для того, чтобы привести их снова к единице на внешнем цилиндре.
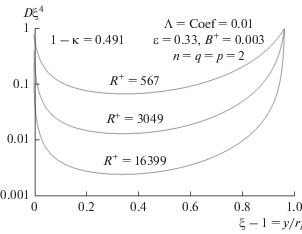
Вихревая вязкость должна обнулиться на обеих твердых поверхностях, а в середине текучей среды она максимальна. Из работы [1] мы знаем, что при больших значениях $R_{i}^{ + }$ профили должны слиться в предельную кривую. Это достигается подстановкой $R_{i}^{ + }$ в знаменатель члена затухания.
Из графика на рис. 6 с логарифмической шкалой по оси ординат ясно, что профили рассеяния в центральной области имеют одинаковую форму, но на двух твердых стенках они вынуждены перейти в граничные условия. Вдали от стенок затухание вынуждает рассеяние уменьшиться. Иначе полное трение (или скручивание) было бы намного выше.
Корректные тенденции дает диссипативная теорема. Она предоставляет способ для расчета профилей рассеяния и вихревой вязкости в областях далеко от стенок. Это хорошо видно на рис. 7, который показывает эмпирический фактор с единственным показателем степени для числа Рейнольдса, но теперь здесь различные данные сведены против безразмерной ширины зазора, 1 – κ. Видны индивидуальные значения 1 – κ; разброс точек для каждого значения 1 – κ связан с тем, что мы не использовали наилучший показатель степени n для каждого значения 1 – κ (он также связан с естественным разбросом этих данных). Но все же видны и отклоняющиеся точки, например при 1 – κ = 0.633.
ТЕЧЕНИЕ В ТРУБЕ
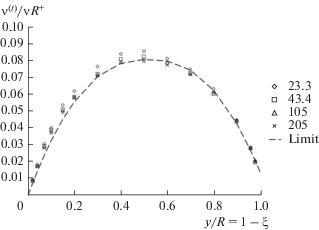
Второй пример – это устоявшееся полностью развитое течение в трубе. К счастью, Никурадзе в 1932 г. [1] опубликовал многочисленные и очень точные данные в широком диапазоне чисел Рейнольдса. Он пытался вести исследования и при очень высоких числах Рейнольдса, потому что имевшиеся в то время данные никогда не выходили на прямую на билогарифмическом графике зависимости коэффициента трения от числа Рейнольдса. Никурадзе открыл асимптотическую область, которая показала истинно предельное поведение, что привело к заключению о том, что больше нет необходимости переходить к высоким числам Рейнольдса, потому что предельное поведение уже ясно. Он точно измерил профили скорости и вихревой вязкости, а также коэффициенты полного трения для потока. Уже было известно, что, если отложить зависимость обратной величины квадратного корня из трения на линейной шкале от числа Рейнольдса, умноженного на квадратный корень из коэффициента трения, то мы получим прямую линию. Эти данные ясно показывают, что вихревая вязкость проходит через максимум приблизительно на полпути между стенкой и осью трубы. Затем она уменьшается, стремясь к нулю, но не достигает его. Рисунок 8 показывает данные для четырех промежуточных значений числа Рейнольдса. Это – неоценимое руководство для понимания природы турбулентного течения, и оно показывает дальнейшее развитие диссипативной теоремы (см. работы [10, 11]).
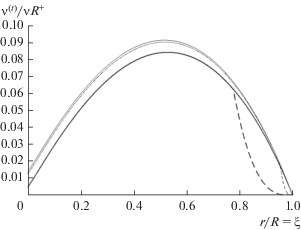
Рис. 8.
Экспериментальный профиль вихревой вязкости [1]. Никурадзе исследовал поток в трубе для 16 чисел Рейнольдса от 4000 до 3 200 000. Этот график показывает четыре промежуточных числа Рейнольдса и приближенную предельную кривую для очень высоких чисел Рейнольдса. Значения [1, 11] для более низких чисел Рейнольдса лежат все выше и выше этой предельной кривой. Для того чтобы эти профили слились в предельную кривую, следует делить значения ν(t)/ν на R+.
Для того чтобы получить согласие c экспериментальными результатами, представим член, описывающий затухание, как
(10)
${\text{decay}} = \frac{{\rho {{R}^{{\text{2}}}}}}{{\tau _{{\text{0}}}^{{\text{2}}}}}{\text{Decay}} = \Lambda {{\left( {\frac{{D{{R}^{ + }}}}{\xi }} \right)}^{{\text{2}}}} + \Lambda \varepsilon \frac{D}{{{{R}^{ + }}}}{\text{ }},$На рис. 9 показаны несколько профилей вихревой вязкости, вычисленных на основе диссипативной теоремы. Поток в трубе отличается от такового в системе вращающихся цилиндров не тем, что один из них вращается, а тем, что напряжение сдвига обнуляется в центре трубы, в то время как в системе вращающихся цилиндров оно никогда не равно нулю, а в тонких зазорах остается постоянным.
Рис. 9.
Профили вихревой вязкости, вычисленные на основе диссипативной теоремы. Эти кривые вычислены со следующими параметрами: Coef = Λ = 0.17, n = p = q = 2, B+ = 0.0005, ε = 0.33. Кривые для R+ of 88198, 16399, 3049 и 567 накладываются друг на друга, а кривая для 105 лежит немного ниже. (Напротив, экспериментальные данные Никурадзе для низких значений R+ лежат выше предельной кривой на рис. 8.) Сплошные кривые рассчитаны по диссипативной теореме без учета области y3. Пунктирные кривые для R+ = 567 и 105 демонстрируют эффект стыковки в области y3. При R+ = 105 он распространяется от r/R = 1 до, приблизительно, 0.8, а при R+ = = 567 – на гораздо меньшую область (сравн. рис. 1). В левой части эти кривые напоминают кривые Никурадзе на рис. 8, с той разницей, что они не идут в ноль на осях. Это достигается с помощью параметра ε, введенного в настоящей работе.
На рис. 10 показано безразмерное рассеяние, рассчитанное из профилей вихревой вязкости, полученных Никурадзе (см. рис. 8). Пунктирная линия – результат ламинарного течения в трубе. Затухание сильно понижает рассеяние, которое, таким образом, остается очень высоким только вблизи стенки. Подгонка члена, описывающего затухание (на основе измеренных Никурадзе профилей вихревой вязкости), отражается на форме уравнения (10). Пунктирная кривая с короткими штрихами на рис. 10 показывает, каким образом вычисленное затухание может приблизиться к затуханию ламинарного потока (следовательно, дать нулевую вихревую вязкость), если положить параметр ε равным нулю и не подгонять значения Λ.
Рис. 10.
Безразмерное рассеяние для некоторого диапазона значений параметра напряжения R+, вычисленное из набора кривых для вихревой вязкости. Все кривые начинаются при 1 на стенке (r/R = 1). Более высокие значения R+ вызывают более крутой спад объемного рассеяния и потому отстоят дальше от области отрицательной вихревой вязкости. Сплошные линии следуют предельной кривой Никурадзе на рис. 8. Пунктирные кривые с короткими штрихами возникают при “навязывании” предельной кривой Никурадзе нулевой вихревой вязкости на центральной линии; они асимптотически приближаются к прямой для ламинарного течения вблизи оси. Это означает, что картина рассеяния, предсказывающая поведение вихревой вязкости, с большей вероятностью касается прямой для ламинарного течения. Эти кривые рассеяния имеют одинаковую форму в данной шкале, за исключением области вблизи стенки, где, согласно граничному условию, D = ${{\mu {{\mathcal{D}}_{V}}} \mathord{\left/ {\vphantom {{\mu {{\mathcal{D}}_{V}}} {\tau _{0}^{{\text{2}}}}}} \right. \kern-0em} {\tau _{0}^{{\text{2}}}}}$ = 1.
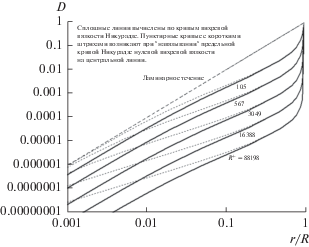
Постоянная проблема – предсказывание отрицательной вихревой вязкости. Это помогает понять, что отрицательные значения возникают, если рассчитанная кривая затухания пересекается с прямой для ламинарного течения; в конце концов, измеренные Никурадзе профили вихревой вязкости помогли решить проблему.
Исходно, мы ожидали, что вихревая вязкость будет максимальной на центральной оси, но экспериментальные результаты Никурадзе (рис. 8) показывают, что в действительности вихревая вязкость проходит через максимум и на оси приближается к небольшой, но ненулевой величине. Это затухание увеличивается, когда рассеяние у стенки велико; оно увеличивается еще быстрее вблизи оси (благодаря члену ξ2 в знаменателе уравнения (10)). Форма кривой затухания на рис. 10 отражает уменьшение значения D в направлении к оси, но также и увеличение затухания из-за радиального положения точки. Если значение D становится очень маленьким, затухание сильно уменьшается, и кривая может пересекаться с прямой для ламинарного течения.
Коэффициент трения в потоке в трубе можно вычислить по следующему уравнению [11]:
(11)
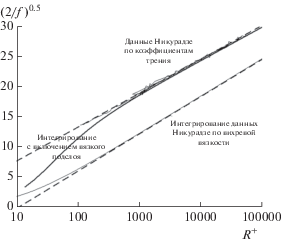
$\sqrt {\frac{2}{f}} = {{R}^{ + }}\int\limits_0^1 {\frac{{{{\xi }^{3}}d\xi }}{{1 + {{R}^{ + }}M(\xi )}},} $Рис. 11.
График коэффициента трения, вычисленного из распределения вихревой вязкости, построенный в соответствии с законом универсального сопротивления, который предположительно должен быть представлен прямой линией. Искривление внизу – следствие непосредственного интегрирования уравнения (11) с вихревой вязкостью, измеренной Никурадзе, с меньшим шагом интегрирования для бóльших значений R+. Другая кривая вычислена по программе рассеяния, с существенным использованием профилей вихревой вязкости из рис. 9, но с включением y3-области. Эта кривая поднимается от нижней кривой и в конце концов приближается к прямой, лежащей намного выше, чем асимптота нижней кривой. (Здесь Λ = 0.17, n = p = q = 2, B+ = 0.0005. Эта кривая не модифицирована, если значение ε не равняется нулю и обработано так же, как на рис. 9.) Прямые описываются, как (2/f)0.5 = 2.7 ln(R+) – 6.46 (нижняя) и 2.45 ln(R+) + 2 (верхняя), что находится в хорошем согласии с фитингом экспериментальных данных Никурадзе по коэффициентам трения, который охватывает диапазон от R+ = 112 до 56 000. Прямая, построенная Никурадзе, согласуется с приведенными данными и в то же время выходит за их пределы.
ТЕЧЕНИЕ ВДОЛЬ ПЛОСКОЙ ПЛАСТИНКИ
Следующие два примера касаются развитого потока, который вначале представляет собой ламинарный поток, за этим следует переход к турбулентности и далее к полностью развитой турбулентности. Первый из двух примеров – это поток вдоль плоской пластинки при нулевом угле набегания, другой – поток к вращающемуся диску. Рисунок 12 – это набросок системы с плоской пластинкой. В этих двух примерах распределение напряжения заранее не известно, в отличие от потоков на вращающихся цилиндрах и в трубе. Поэтому следует включить в рассмотрение уравнение непрерывности и по крайней мере один тангенциальный компонент уравнения сохранения количества движения, в дополнение к уравнению напряжений, соотношению между рассеянием и вихревой вязкостью и диссипативной теореме. Понадобится также вихревой коэффициент диффузии, если только не положить его равным вихревой кинематической вязкости.
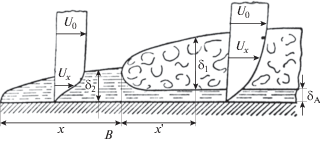
Рис. 12.
Схема различных областей течения вдоль плоской пластинки в однородном потоке (взятая из работы [12]). Вблизи пеpедней кpомки течение ламинарное. Здесь x' обозначает область перехода к турбулентности, а правее находится область развитой турбулентности, которую нам предстоит охарактеризовать. Имеется также небольшая эллипсовидная область очень близко к пеpедней кpомке. На заданном расстоянии вниз по течению в области турбулентности вблизи пластинки имеется тонкий вязкий подслой, в котором значение вихревой кинематической вязкости не равно нулю, но меньше кинематической вязкости. За пределами этой области имеется другая, в которой кинематическая вязкость меньше вихревой кинематической вязкости. Еще дальше имеем область, где остается некоторая турбулентность, но средняя тангенциальная скорость достигает того значения, которое она имеет в свободном потоке. (Рисунок показывает, что величина U0 одинакова в обоих положениях на пластинке.) Область значительной вихревой кинематической вязкости может простираться на большое расстояние от пластинки, но это не оказывает существенного влияния на среднее течение, потому что напряжение и градиент средней скорости малы.
Решение Блазиуса описывает ламинарный пограничный слой, толщина которого возрастает с ростом корня квадратного из расстояния x вдоль пластинки, а напряжение у стенки τ0 уменьшается с обратной величиной этого корня квадратного. Мы сочли целесообразным выразить проблему, используя систему координат, предложенную Блазиусом. Так, в качестве переменных безразмерного расстояния по нормали и тангенциального расстояния мы использовали
(12)
$\eta = y\sqrt {\frac{{{{v}_{\infty }}}}{{\nu x}}} {\text{ и }}\chi = \frac{{x{{v}_{\infty }}}}{\nu } = {{\operatorname{Re} }_{x}}.$А для компонентов скорости – по нормали и тангенциальной – величины
(13)
${{\bar {v}}_{x}} = {{v}_{\infty }}\frac{{\partial f(\chi ,\eta )}}{{\partial \eta }}{\text{ и }}{{\bar {v}}_{y}} = \sqrt {\frac{{\nu {{v}_{\infty }}}}{x}} \left[ {\frac{\eta }{2}\frac{{\partial f}}{{\partial \eta }} - \frac{f}{2} - \chi \frac{{\partial f}}{{\partial \chi }}} \right],$(14)
$T = \frac{\tau }{\mu }\sqrt {\frac{{\nu x}}{{v_{\infty }^{{\text{3}}}}}} ,{\text{ }}D = \frac{{x{{\mathcal{D}}_{V}}}}{{\rho v_{\infty }^{{\text{3}}}}}{\text{ и }}G = \frac{{\nu + {{\nu }^{{(t)}}}}}{\nu }.$Основное дифференциальное уравнение, после преобразования координат от x, y к χ, η, – это уравнение сохранения количества движения (в комбинации с уравнением непрерывности)
(15)
$2f{\kern 1pt} '\chi \frac{{\partial f{\kern 1pt} '}}{{\partial \chi }} - 2f{\kern 1pt} ''\chi \frac{{\partial f}}{{\partial \chi }} = ff{\kern 1pt} ''\,\, + {\text{ }}2\frac{{\partial Gf{\kern 1pt} ''}}{{\partial \eta }},$(16)
$\begin{gathered} 2f{\kern 1pt} '\chi \frac{{\partial D}}{{\partial \chi }} - 2\frac{{\partial D}}{{\partial \eta }}\chi \frac{{\partial f}}{{\partial \chi }} = 2Df{\kern 1pt} '\,\, + \\ + \,\,f\frac{{\partial D}}{{\partial \eta }} + 2\frac{\partial }{{\partial \eta }}\left( {G\frac{{\partial D}}{{\partial \eta }}} \right) - 2\Lambda \frac{{{{\chi }^{{2 - n}}}{{D}^{n}}}}{{{{\xi }^{p}}{{{({{R}^{ + }})}}^{q}}}}, \\ \end{gathered} $(19)
$f{\kern 1pt} ' = {{\left( {\frac{{\partial f}}{{\partial \eta }}} \right)}_{\chi }}{\text{ и }}f{\kern 1pt} '' = {{\left( {\frac{{\partial f{\kern 1pt} '}}{{\partial \eta }}} \right)}_{\chi }}.$Следует понимать, что для любой производной величина χ поддерживается постоянной по отношению к η, и обратно. После того, как преобразование координат завершено, остаются только эти две независимые переменные.
Для ламинарного потока уравнение (15) сводится к уравнению Блазиуса, в котором f не зависит от x, и где ν(t) = 0. Таким образом, это уравнение решается, начиная с x = 0. После того, как введена вихревая вязкость, решение уравнения отклоняется от решения уравнения Блазиуса. Для того, чтобы выполнить такое введение вихревой вязкости, потребуется использовать и другие уравнения.
Смысл множителей в члене, описывающем затухание, в уравнении (16) остается неясным. Один из них замещает ξ напряжением T, в соответствии с потоком в трубе. Для замещения R+ существуют три кандидата. Один из них – это χ, другой – x+ = (x/ν)(τ0/ρ)0.5. Оба вносят в член, описывающий затухание, зависимость от x. Третья возможность – это (τ0/ρ)0.5/v∞ – член, сохраняющий присутствие напряжения у стенки, но не включающий расстояния x. Мы придерживаемся последнего. Можно также ввести член εD, как в уравнении (10), но это может повлечь за собой нежелательную зависимость от x в члене, описывающем затухание.
Численное решение оказалось непростой задачей. Для случая полностью развитой турбулентности полезен метод обратного замещения. Считая профиль G известным, начнем с предположения о том, что G = 1. Если величина G определена, то другие уравнения оказываются более устойчивыми. Это означает, что уравнение (18) не используется в данном процессе, но после нахождения профилей f, f′, T и D получаем из уравнения (18) и известных теперь профилей T и D новую догадку о профиле G. После проведения нескольких итераций вычисленный профиль G согласуется со сделанным ранее предположением, чем и достигается сходимость.
Заключение о развитии потока с расстоянием x остается задачей на будущее.
В ламинарном потоке G = 1, и уравнение (18) показывает, что величина D должна быть равной T 2. Однако значение D, вычисленное на основе диссипативной теоремы, не равняется T 2. Это расхождение послужило движущей силой для возникновения турбулентности. Оно также означает, что всякий раз, когда D = T 2, вихревая вязкость равняется нулю подобно тому, как это происходит в потоке в трубе (см. рис. 10).
Одна из проблем заключается в том, что кривая для D может пересекать кривую для T 2. Это означает, что вихревая вязкость упала до нуля. Поскольку такое утверждение лишено физического смысла, положим величину G равной 1. Тогда появляется резкая разделительная линия между областью с вихревой вязкостью и областью, где ее нет. Если сфокусировать внимание на полностью развитом потоке, то вышеприведенные уравнения решаются без производных по χ. Таким образом, единственной независимой переменной остается η, а параметры возникают только из затухания.
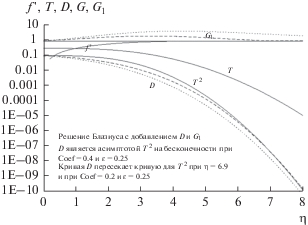
Рисунок 13 иллюстрирует течение Блазиуса (с G = 1), а также показывает возможность вычисленной кривой для D пересекать кривую для T2, что подразумевает отрицательные значения вихревой вязкости.
Рис. 13.
Решение Блазиуса для ламинарного потока с G = 1. Значения T и f ' не зависят от параметров затухания. Значения D не согласуются с T 2, в отличие от того, что имеет место в ламинарном потоке. Кривая для параметров затухания D (пунктирная кривая с длинными штрихами) пересекает кривую T 2, поэтому оценка профиля G1 дает 1 при конечном значении η. Кривые для параметров затухания (пунктирная кривая с короткими штрихами) не пересекаются, поэтому профиль G1 (оценка) простирается гораздо дальше, возможно, даже в бесконечность.
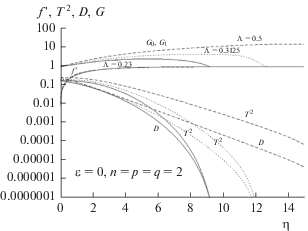
На рис. 14 показаны три сходящиеся решения для полностью развившегося турбулентного течения вдоль плоской пластинки при Λ = 0.23, 0.3125 и 0.5, все – при ε = 0. Для каждого G0 = G1. Подбором величины Λ можно продлить область турбулентности еще дальше. Профиль f′ мало изменяется; он продлевается немного дальше, чем в случае решения Блазиуса на рис. 13, а его значение T у стенки повышается. Поскольку безразмерная тангенциальная скорость на бесконечности равняется 1, то маловероятно, что профиль изменится. Профили D и T2 простираются гораздо дальше, чем на рис. 13, они несколько спрямляются, демонстрируя спад по экспоненте с расстоянием.
Рис. 14.
Сходящиеся решения для полностью развившегося турбулентного течения вдоль плоской пластинки. Это означает, что с ростом x график остается без изменения, но толщина пограничного слоя продолжает увеличиваться с ростом корня квадратного из расстояния вдоль пластинки (сравн. рис. 12).
Следует отметить, что значение T при η = 0 в действительности не представляет собой напряжения на пластинке. Другими словами, вязкий подслой вносит касательную составляющую скорости на поверхности, где диссипативная теорема не рассматривает y3-поведения в вязком подслое. Рисунок 11 показывает, что в вязком подслое существует значительное напряжение, и его следует принимать во внимание при определении коэффициента трения.
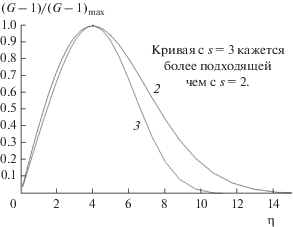
Здесь хорошо было бы следовать за развивающимся турбулентным пограничным слоем. Но с этим придется повременить. Вычисление больших значений χ займет много времени. Также, предварительные результаты показывают, что турбулентность наступает раньше, чем следует из эксперимента, а фрикционные свойства вязкого подслоя еще не реализуются. Компьютерная программа легко найдет профиль, но он неустойчив. Можно думать, что профиль, при котором кривая для D пересекает кривую для T2, не подходит. Однако, если кривая для D не дает пересечения, а вместо этого уходит намного ниже кривой для T2, то уравнение (18) приводит к очень большим значениям для вихревой вязкости, содержащимся в G. Рисунок 15 дает профиль, показывающий ожидаемое поведение величины G – 1 как функции η; она возрастает до своего максимального значения, а затем постепенно уменьшается до нуля. После достижения максимума она больше не возрастает.
Рис. 15.
Ожидаемое поведение вихревой вязкости G – 1 на плоской пластинке. Форма, которая выглядит похожей на вычисленные профили, может быть описана следующим соотношением:
$\frac{{G - 1}}{{{{{(G - 1)}}_{{{\text{max}}}}}}} = \frac{\eta }{{H\exp ( - 1{\text{/}}s)}}\exp [ - {{({\eta \mathord{\left/ {\vphantom {\eta {sH}}} \right. \kern-0em} {sH}})}^{s}}],$ (20)
где H – это значение η в максимуме, а s – постоянная. При этом s = 3 воспроизводит желаемую форму лучше, чем s = 2.
ПОТОК НА ВРАЩАЮЩИЙСЯ ДИСК
Четвертый пример – это вращающийся диск, излюбленное орудие исследования электрохимических систем. Публикации [13–15] охватывают часть более ранних исследований турбулентности с помощью этого метода. Экспериментально он, вероятно, гораздо удобнее, чем большая плоская пластина в аэродинамической трубе, потому что он компактен, и его легче поддерживать чистым. Анализ этого должен быть во многом подобен случаю плоской пластинки, и он может быть в равной степени труден.
ОДНОРОДНАЯ ИЗОТРОПНАЯ ТУРБУЛЕНТНОСТЬ
В 1941 г. Колмогоров [2] опубликовал теоретическое предсказание того, как затухает однородная изотропная турбулентность. Он утверждал, что вихри большого размера не подвергаются воздействию вязкости. Они разбиваются друг о друга, и получаются вихри небольшого размера. Однако, кинетическая энергия в этих вихрях остается той же. Этот процесс продолжается до тех пор, пока вихри не сделаются очень маленькими, так что вязкость преобразует кинетическую энергию в тепловую. Этот процесс должен быть тесно связан с затуханием рассеяния, описанным в настоящей работе.
ВЯЗКИЙ ПОДСЛОЙ
Весьма интересно, что же происходит в непосредственной близости от поверхности в турбулентном потоке вязкой среды. В 1932 г., а затем снова в 1942 г. предположили, что течение в этой области не ламинарное; напротив, вихревая вязкость постепенно уменьшается с расстоянием от поверхности. Имеется разночтение в вопросе о том, меняется ли вихревая вязкость при удалении от поверхности по закону третьей или четвертой степени. На самом деле вихревая вязкость пропорциональна кубу расстояния очень близко к поверхности, а вблизи внешней границы вязкого подслоя – четвертой степени. Это видно на рис. 16 [16, 17].
Рис. 16.
Профили вихревой вязкости в области вблизи стенки в турбулентном потоке вязкой среды [16, 17]. На профили наложены пунктирные линии с наклонами 1, 3 и 4, в предположении о том, что величина ${{\mathcal{D}}^{{(t)}}}$/ν пропорциональна y3 в непосредственной близости от стенки, пропорциональна y4 внутри вязкого подслоя и пропорциональна y сразу за его пределами в турбулентном потоке. Также добавлены точки, указывающие толщину диффузионного слоя для различных чисел Шмидта. Толщину определили как расстояние, при котором ${{\mathcal{D}}^{{(t)}}} = \mathcal{D}$. Точка для Sc = 100 лежит непосредственно левее области графика, а точка для Sc = 1000 – на значительном расстоянии левее его.
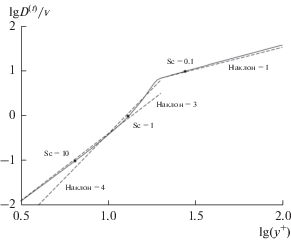
В сравнении с рис. 1 можно заметить, что горизонтальная линия для ν на рис. 1 становится горизонтальной линией для $\mathcal{D}$ на рис. 16 при значении ординаты 1/Sc. Это дает больший диапазон y, в котором можно изучать вихревой коэффициент диффузии в вязком подслое, хотя это и не включает непосредственного измерения ${{\mathcal{D}}^{{(t)}}}$.
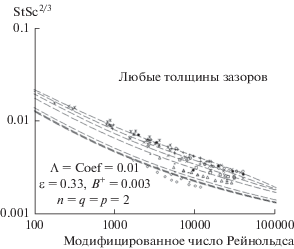
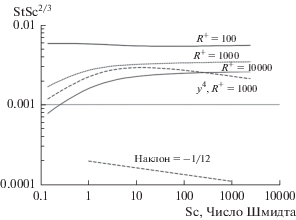
Будем надеяться, что рис. 16 разрешит это противоречие. В литературе ряд статей высказывается в пользу y4-зависимости, но экспериментальные результаты по массопереносу при высоких числах Шмидта (в том числе полученные в системе с вращающимся цилиндром, см. рис. 3), в общем и целом, указывают на y3-зависимость. Упомянем здесь, что число Стентона почти пропорционально числу Шмидта в степени –2/3, что следует из y3-зависимости вихревого коэффициента диффузии, но не из y4-зависимости. Скорость массопереноса отражает среднее значение вихревого коэффициента диффузии по толщине диффузионного слоя. На рис. 17 представлены вычисленные значения StSc2/3, как функция Sc, для потока в трубе при различных значениях R+. При высоких Sc наклон кривых приближается к нулю не только, если они вычислены на основе y3-зависимости в диффузионном слое, но и если они вычислены из профиля ${{\mathcal{D}}^{{(t)}}}$/ν, показанного на рис. 16. Только кривая, вычисленная на основе существования y4-зависимости на всей толщине диффузионного слоя, имеет наклон –1/12 при высоких Sc, показывая этим, что она является асимптотической формой кривых, которые проявляются наиболее ясно, и что детальное поведение в середине не очень важно. (Для сравнения приведена линия с наклоном –1/12.) Наклоны, различающиеся только на 1/12, нелегко распознавать экспериментально, тем более, что данные по массопереносу часто представляют в форме зависимости от числа Рейнольдса вместо того, чтобы строить график, как зависимость от числа Шмидта.
Рис. 17.
График демонстрирует, каким образом вихревой коэффициент диффузии влияет на скорость массопереноса в трубе при постоянном потоке у стенки. Сплошные линии показывают зависимость числа Стентона от числа Шмидта для трех значений параметра напряжения R+: 100, 1000 и 10 000 (соответствующих числам Рейнольдса 2245, 36 105 и 378 600). Для этих кривых вихревой коэффициент диффузии в вязком подслое пропорционален y3. Пунктирная кривая с длинными штрихами соответствует y4-зависимости в вязком подслое; ее наклон при больших числах Шмидта равняется –1/12. Пунктирная кривая с короткими штрихами использует для вихревого коэффициента диффузии зависимость, приведенную в работе [18] (уравнение (15.71)). Существенно, что она совпадает с кривой для такого же значения R+, но с простой y3-пропорциональностью в вязком подслое. При больших Sc обе кривые имеют нулевой наклон и никогда не показывают наклона равного –1/12.
Статистическая обработка флуктуаций в вязком подслое существенно проясняет поведение вихревого коэффициента диффузии и вихревой вязкости в этой области [19–21]. Вихревая вязкость следует y3-зависимости в большей части вязкого подслоя, но вихревой коэффициент диффузии сильнее структурирован и зависит от числа Шмидта. В то же время эти две величины могут быть существенно одинаковы во внешнем турбулентном потоке (т.е., за пределами вязкого подслоя), а ${{\mathcal{D}}^{{(t)}}}$ может сделаться намного меньше, чем ν(t), тем больше, чем больше число Шмидта.
Левич в своей книге [12, глава 4, стр. 29] пишет: “В вязком подслое величина Re меньше единицы, и члены второго порядка в уравнении Навье–Стокса малы по сравнению с членами первого порядка. Поэтому распределение скоростей в вязком подслое может определяться только линейными уравнениями. Когда некоторый спектр вихрей проникает в вязкий подслой, взаимодействие между отдельными вихрями прекращается. При этом поток превращается в сумму независимых периодических движений, период которых T остается постоянным во всем вязком подслое.”
Мартемьянов, Воротынцев и Графов [18, 19] рассмотрели вязкий подслой и сделали заключение о том, что вихревая вязкость пропорциональна y3, но вихревой коэффициент диффузии в вязком подслое начинает отклоняться от вихревой кинематической вязкости, демонстрируя y4-зависимость внутри этого подслоя вблизи его границы, но глубоко внутри него существует y3-зависимость, причем этот коэффициент зависит от коэффициента диффузии $\mathcal{D}$. Они заключили, что в области y3-зависимости вихревой коэффициент пропорционален корню квадратному из $\mathcal{D}$. Мартемьянов в работе [20] подытожил статистическое рассмотрение вязкого подслоя.
Анализируя турбулентный поток, обычно записывают все свойства потока, как сумму стационарной и флуктуационной части, например,
Уравнение для флуктуаций скорости обычно выводят, вначале усредняя уравнение сохранения количества движения, а затем вычитая этот результат из не усредненного уравнения. В результате получается:
(22)
$\begin{gathered} \frac{{\partial {\mathbf{v}}{\kern 1pt} '}}{{\partial t}} + \nabla \cdot {\mathbf{\bar {v}v}}{\kern 1pt} '\,\, + \nabla \cdot {\mathbf{v}}{\kern 1pt} '{\mathbf{\bar {v}}} + \nabla \cdot {\mathbf{v}}{\kern 1pt} '{\mathbf{v}}{\kern 1pt} ' - \nabla \cdot \left\langle {{\mathbf{v}}{\kern 1pt} '{\mathbf{v}}{\kern 1pt} '} \right\rangle = \\ = \nu \nabla \cdot \nabla {\mathbf{v}}{\kern 1pt} ' - \frac{1}{\rho }\nabla \mathcal{P}{\kern 1pt} ', \\ \end{gathered} $(23)
$\frac{{\partial {{c}_{i}}}}{{\partial t}} + \nabla \cdot ({\mathbf{v}}{{c}_{i}}) = \mathcal{D}\nabla \cdot \nabla {{c}_{i}}$(24)
${{c}_{i}} = {{c}_{0}}\,\,\,{\text{при}}\,\,\,y = 0\,\,\,\,{\text{и}}\,\,\,\,{{c}_{i}} \to {{c}_{\infty }}\,\,\,\,{\text{при}}\,\,\,\,y \to \infty ,$Полная система уравнений для флуктуаций скорости, давления и концентрации такова:
(26)
$\frac{{\partial v_{x}^{'}}}{{\partial x}} + \frac{{\partial v_{y}^{'}}}{{\partial y}} + \frac{{\partial v_{z}^{'}}}{{\partial z}} = 0.$(27)
$\begin{gathered} \frac{{\partial v_{x}^{'}}}{{\partial t}} + \beta y\frac{{\partial v_{x}^{'}}}{{\partial x}} + \beta v_{y}^{'} = \\ = \nu \left( {\frac{{{{\partial }^{2}}v_{x}^{'}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}v_{x}^{'}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}v_{x}^{'}}}{{\partial {{z}^{2}}}}} \right) - \frac{1}{\rho }\frac{{\partial{ \mathcal{P}}{\kern 1pt} '}}{{\partial x}}. \\ \end{gathered} $(28)
$\begin{gathered} \frac{{\partial v_{y}^{'}}}{{\partial t}} + \beta y\frac{{\partial v_{y}^{'}}}{{\partial x}} = \\ = \nu \left( {\frac{{{{\partial }^{2}}v_{y}^{'}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}v_{y}^{'}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}v_{y}^{'}}}{{\partial {{z}^{2}}}}} \right) - \frac{1}{\rho }\frac{{\partial{ \mathcal{P}}'}}{{\partial y}}. \\ \end{gathered} $(29)
$\frac{{\partial v_{z}^{'}}}{{\partial t}} + \beta y\frac{{\partial v_{z}^{'}}}{{\partial x}} = \nu \left( {\frac{{{{\partial }^{2}}v_{z}^{'}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}v_{z}^{'}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}v_{z}^{'}}}{{\partial {{z}^{2}}}}} \right) - \frac{1}{\rho }\frac{{\partial {\kern 1pt} \mathcal{P}'}}{{\partial z}}.$(30)
$\frac{{\partial \theta {\kern 1pt} '}}{{\partial t}} + \beta y\frac{{\partial \theta {\kern 1pt} '}}{{\partial x}} + {\text{v}}_{y}^{'}\frac{{\partial{ \bar {\theta }}}}{{\partial y}} = \mathcal{D}\left( {\frac{{{{\partial }^{{\text{2}}}}\theta {\kern 1pt} '}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{{\text{2}}}}\theta {\kern 1pt} '}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{{\text{2}}}}\theta {\kern 1pt} '}}{{\partial {{z}^{2}}}}} \right).$Уравнение (30) существенно идентично уравнению (6) в работе [21]. Это создает проблему линейности при варьировании флуктуаций, если известны средние величины. Благодаря малой толщине вязкого подслоя, мы аппроксимируем средние профили скорости, как ${{\bar {v}}_{x}}$ = βy, где β – константа, а ${{\bar {v}}_{y}}$ = ${{\bar {v}}_{z}}$ = 0. Средняя концентрация также зависит только от y. Из третьего члена уравнения (30) мы видим, что флуктуации концентрации возникают благодаря взаимодействию флуктуаций скорости с градиентом средней концентрации. Флуктуации концентрации пренебрежимо малы вне диффузионного слоя, который очень тонок при высоких Sc (см. рис. 16).
Поскольку задача линейна и изменяется синусоидально во времени и по направлениям x и z, мы можем использовать преобразование Фурье для того, чтобы разделить поведение различных спектральных компонентов.
(34)
$\mathcal{P}{\kern 1pt} ' = \operatorname{Re} \{ P(y)\exp (i{{k}_{x}}x + i{{k}_{z}}z + i\omega t)\} .$(35)
$\theta {\kern 1pt} ' = \operatorname{Re} \{ C(y)\exp (i{{k}_{x}}x + i{{k}_{z}}z + i\omega t)\} .$Далее мы сделаем задачу безразмерной, вводя y+ = (y/ν)(τ0/ρ)0.5 и безразмерные коэффициенты Фурье и безразмерное давление. Функции скорости Vx, Vy и Vz можно понять, разделив их на значение Vx при y = δ0. Эти параметры и зависимые переменные определены следующим образом:
(36)
${{K}_{x}} = {{k}_{x}}\frac{\nu }{{v{\text{*}}}},\,\,\,\,{{K}_{z}} = {{k}_{z}}\frac{\nu }{{v{\text{*}}}}{\text{,}}\,\,\,\,{\text{где}}\,\,\,\,v* = \sqrt {\frac{{{{\tau }_{0}}}}{\rho }} .$(37)
$\Omega = \omega {\text{ }}\frac{\nu }{{{{{\left( {v{\text{*}}} \right)}}^{2}}}}{\text{,}}\,\,\,\,B = \beta {\text{ }}\frac{\nu }{{{{{\left( {v{\text{*}}} \right)}}^{2}}}}\,\,\,\,{\text{и}}\,\,\,\,p = \frac{P}{{\rho v{\text{*}}}}.$Параметры v*, ρ и τ0 исключаются из уравнения, и задача упрощается с помощью безразмерных переменных Фурье Kx, Kz и Ω. Подстановка уравнений (31)–(35) в уравнения (26)–(30) для каждого спектрального компонента по отдельности (каждый спектральный компонент – это переменные Vx, Vy, Vz, p и C для данного набора Kx, Kz и Ω) дает систему обыкновенных дифференциальных уравнений:
(39)
$\begin{gathered} i\Omega {{V}_{x}} + B{{y}^{ + }}i{{K}_{x}}{{V}_{x}} + B{{V}_{y}} = \\ = - K_{x}^{2}{{V}_{x}} + \frac{{{{d}^{2}}{{V}_{x}}}}{{d{{y}^{{ + 2}}}}} - K_{z}^{2}{{V}_{x}} - i{{K}_{x}}p. \\ \end{gathered} $(40)
$\begin{gathered} i\Omega {{V}_{y}} + B{{y}^{ + }}i{{K}_{x}}{{V}_{y}} = \\ = - K_{x}^{2}{{V}_{y}} + \frac{{{{d}^{2}}{{V}_{y}}}}{{d{{y}^{ + }}^{2}}} - K_{z}^{2}{{V}_{y}} - \frac{{dp}}{{d{{y}^{ + }}}}. \\ \end{gathered} $(41)
$\begin{gathered} i\Omega {{V}_{z}} + B{{y}^{ + }}i{{K}_{x}}{{V}_{z}} = \\ = - K_{x}^{2}{{V}_{z}} + \frac{{{{d}^{2}}{{V}_{z}}}}{{d{{y}^{{ + 2}}}}} - K_{z}^{2}{{V}_{z}} - i{{K}_{z}}p. \\ \end{gathered} $(42)
$\begin{gathered} i\omega C + \beta yi{{k}_{x}}C + {{V}_{y}}\frac{{\partial{ \bar {\theta }}}}{{\partial y}} = \\ = \mathcal{D}\left( { - k_{x}^{2}C + \frac{{{{d}^{{\text{2}}}}C}}{{d{{y}^{2}}}} - k_{z}^{2}C} \right). \\ \end{gathered} $На рис. 18 показаны величины спектральных компонентов для скорости и давления при Kx = = Kz = Ω = 1. Величины флуктуаций концентрации показаны на рис. 19 для нескольких значений числа Шмидта.
Рис. 18.
Вычисленные профили флуктуирующих компонентов скорости и давления для одного компонента спектра Фурье (при Kx = Kz = Ω = 1). Здесь B принято равным 1. Vx, Vy и Vz приняты равными нулю у стенки. Vx и Vz и p приняты равными 1 при y+ = 1. В то время как во внешнем турбулентном потоке эти флуктуации сравнимы по величине для всех трех направлений координат, во внутренней части вязкого подслоя компонент по нормали к стенке убывает с наклоном 2 (на билогарифмическом графике), а тангенциальные компоненты почти равны друг другу и изменяются с наклоном равным 1. Флуктуации давления сохраняются почти без изменения на всем протяжении до поверхности.
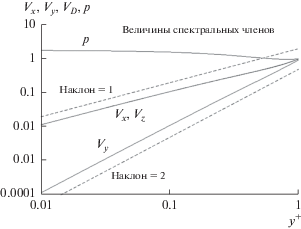
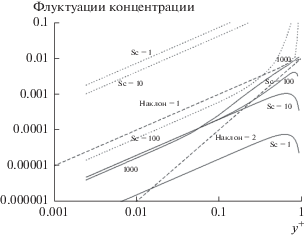
Рис. 19.
Величины флуктуаций концентрации для четырех различных чисел Шмидта Sc, лежащих в диапазоне от 1 до 1000. Сплошные кривые проведены с нулевым граничным условием для C при y+ = $\delta _{0}^{ + }$ = 1. Тогда эти флуктуации концентрации возникают исключительно из-за флуктуаций скорости в вязком подслое. Пунктирные кривые с короткими штрихами полагают величину C, равной 1, при y+ = δ0, что может быть более подходящим для Sc = 1, потому что диффузионный слой может несколько выходить за пределы вязкого подслоя. Для Sc = 1000 эти две кривые почти совпадают, за исключением значений y+, очень близких к $\delta _{0}^{ + }$. Пунктирные кривые дают сравнение наклонов равных 1 и 2.
Напряжение Рейнольдса равняется плотности, умноженной на среднее от произведения флуктуаций y- и x-компонентов скорости. Разделив на плотность и производную от среднего x‑компонента скорости, получим вихревую кинематическую вязкость. Интенсивность потока турбулентного массопереноса равняется среднему от произведения флуктуаций концентрации и y‑компонента скорости. Разделив ее на производную от средней концентрации, получим вихревой коэффициент диффузии (см. рис. 20).
Рис. 20.
Профили относительной величины вихревого коэффициента диффузии ${{\mathcal{D}}^{{(t)}}}$ и вихревой кинематической вязкости ν(t). Число Шмидта является параметром для коэффициента диффузии; опять-таки, для пунктирной кривой с короткими штрихами граничное условие C = 1, а для сплошных линий – C = 0, причем оба граничные условия применяются при y+ = $\delta _{0}^{ + }$ = 1. Эти граничные условия приводят к некоторому искажению вблизи максимального значения. Вихревая кинематическая вязкость располагается сразу над пунктирной кривой с короткими штрихами для Sc = 1. Точечные кривые дают сравнение наклонов, равных 3 и 4.
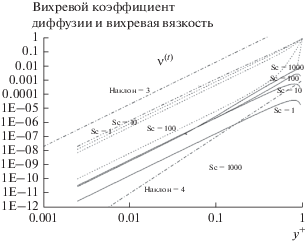
Рисунок 20 можно сравнить с левой стороной рис. 16 для вязкого подслоя. Вихревая кинематическая вязкость демонстрирует почти y3-зависимость по всей толщине вязкого подслоя. Поведение вихревого коэффициента диффузии сильно зависит от величины числа Шмидта. В левой части рисунка он пропорционален y3, но для Sc = 100 и 1000 он демонстрирует y4-зависимость как раз внутри вязкого подслоя, скажем, при y+ между 0.1 и 1. Поскольку толщина диффузионного слоя лежит при ~0.08 для Sc = 1000, то диффузионный слой располагается главным образом внутри y3-области.
Долговременная задача заключается в том, чтобы соотнести турбулентность на некотором расстоянии от стенки с турбулентностью в вязком подслое, т. е. соотнести $B_{{\text{1}}}^{ + }$ и B+, где $B_{{\text{1}}}^{ + }$ – это коэффициент для кривой на правой стороне рис. 16, а B+ – это коэффициент при члене y3 на его левой стороне. Из рис. 20 видно, что это отношение может зависеть от числа Шмидта; точнее, значение B+ при Sc = 1000 может быть в 1000 раз меньше, чем то, которое соответствовало бы наклону y3-члена для вихревой кинематической вязкости. Можно продемонстрировать с помощью рисунка в работе [18] или рис. 16 в настоящей работе кривые для более чем одного значения Sc, а также показать кривую для вихревой кинематической вязкости, которая может быть расположена поверх кривой для ${{\mathcal{D}}^{{(t)}}}$/ν при Sc = 1. Для данных по коэффициенту трения и скручиванию, вместо данных по массопереносу, вероятно, может быть более подходящим другое значение B+.
На больших расстояниях от стенки перестает быть справедливым неучет взаимодействия вихрей (т.е., нелинейных эффектов). Ближе к стенке он сохраняет справедливость и потому дает правильные результаты для диффузии при больших числах Шмидта.
ЗАКЛЮЧЕНИЕ
Искомой является единая теория турбулентного сдвигового течения, в соответствии с которой явления в различных системах (подобных четырем примерам, приведенным в настоящей работе) имеют сходные причины, закрепленные в диссипативной теореме (дополненной теорией вязкого подслоя). Уже на этой стадии кажется, что для различных систем могут потребоваться различные параметры, но в конце концов остается надежда на единство подхода. Одно мы можем утверждать: системы с вращением, будь то вращающийся цилиндр или вращающийся диск, могут и не потребовать разных теорий, если принять в расчет тот факт, что напряжение обнуляется на оси трубы, но не в течении Куэтта или круговом течении Куэтта. Диссипативная теорема дает предсказания для рассеяния и вихревой вязкости на некотором расстоянии от стенки.
Диссипативная теорема не имеет надежного обоснования, но она показала себя лучше, чем можно было ожидать. Полученное Никурадзе объяснение поведения турбулентности в потоке в трубе продемонстрировало, как важно иметь надежные экспериментальные данные. Даже теория Колмогорова должна найти применение в выяснении природы затухания турбулентности.
Список литературы
Nikuradse, J. Gesetzmässigkeiten der turbulenten Strömung in glatten Rohren, Forschungsheft 356, Beilage zu Forschung auf dem Gebiete des Ingenieurwesens, Edition B, vol. 3, September/October 1932 (Berlin NW7: VDI-Verlag GMBH, 1932). Пepeвoд в: Nikuradse, J. Laws of Turbulent Flow in Smooth Pipes, NASA TT F-10, 359, Washington: National Aeronautics and Space Administration, October, 1966.
Kolmogorov, A.N., Dissipation of Energy in Locally Isotropic Turbulence, Doklady Akad. Nauk, 1941, vol. 32, p. 16.
Murphree, E.V., Relation between Heat Transfer and Fluid Friction, Ind. Eng. Chem., 1932, vol. 24, p. 726. https://doi.org/10.1021/ie50271a004
Levich, B. The Theory of Concentration Polarization, I. Acta Physicochimica U.R.S.S., 1942, vol. 17, p. 257.
Levich, B., The Theory of Concentration Polarization, II. Acta Physicochimica U.R.S.S., 1944, vol. 19, p. 117.
Eisenberg, M., Studies of Rates of Solid Dissolution and of Electrode Reactions at Rotating Cylindrical Bodies, dissertation, Berkeley: Univ. California, 1953.
Mohr, C.M., Jr., Mass Transfer in Rotating Electrode Systems, dissertation, Berkeley: Univ. California, 1975.
Newman, J., Theoretical Analysis of Turbulent Mass Transfer with Rotating Cylinders, J. Electrochem. Soc., 2016, vol. 163, p. E191.
Ньюмен, Дж., Турбулентное течение при вращении внутреннего цилиндра. Электрохимия. 2019. Т. 55. С. 51. [Newman, J., Turbulent Flow with the Inner Cylinder Rotating, Russ. J. Electrochem., 2019, vol. 55, p. 44.]
Ньюмен, Дж., Применение диссипационной теоремы к турбулентному течению и массопереносу в трубе. Электрохимия. 2017. Т. 53. С. 1195. [Newman, J., Application of the Dissipation Theorem to Turbulent Flow and Mass Transfer in a Pipe, Russ. J. Electrochem., 2017, vol. 53, p. 1061.]
Ньюмен, Дж., Развитие представлений о турбулентном течении в трубе. Электрохимия. 2019. Т. 55. С. 39. [Newman, J., Further Thoughts on Turbulent Flow in a Pipe, Russ. J. Electrochem., 2019, vol. 55, p. 34. https://doi.org/10.1134/S1023193519010105]
Levich, V.G., Physicochemical Hydrodynamics, Englewood Cliffs, N. J.: Prentice-Hall, 1962.
Mohr, C.M., Jr. and Newman, J., Mass Transfer to a Rotating Disk in Transition Flow, J. Electrochem. Soc., 1976, vol. 123, p. 1687.
Law, C.G., Jr., Pierini, P., and Newman, J., Mass Transfer to Rotating Disks and Rotating Rings in Laminar, Transition, and Fully-developed Turbulent Flow, Int. J. Heat Mass Transfer, 1981, vol. 24, p. 909.
Law, C.G., Jr. and Newman, J, Corrosion of a Rotating Iron Disk in Laminar, Transition, and Fully Developed Turbulent Flow, J. Electrochem. Soc., 1986, vol. 133, p. 37.
Wasan, D.T., Tien, C.L., and Wilke, C.R., Theoretical Correlation of Velocity and Eddy Viscosity for Flow Close to a Pipe Wall, A.I.Ch.E. J., 1963, vol. 9, p. 567.
Ньюмен, Дж., Вихревая диффузия в вязком подслое, Электрохимия. 2019. Т. 55. С. 1272. [Newman, J., Eddy Diffusivity in the Viscous Sublayer, Russ. J. Electrochem., 2019, vol. 55, p. 1031.]
Мартемьянов, С.А., Воротынцев, M.В., Графов, Б.M., Функциональная форма коэффициента турбулентной диффузии в приэлектродном слое. Электрохимия. 1979, Т. 15. № 6. С. 770. [Martem’yanov, S.A., Vorotyntsev, M.A., and Grafov, B.M., Functional Form of the Turbulent Diffusion Coefficient in the Layer next to the Electrode, Soviet Electrochem., 1979, vol. 15, no. 6, p. 790.]
Vorotyntsev, M.A., Martem’yanov, S.A., and Grafov, B.M., Closed equation of turbulent heat and mass transfer, J. Exp. Theor. Phys., 1980, vol. 52, p. 909.
Мартемьянов, С.А., Статистическая теория турбулентного массопереноса в электрохимических системах. Электрохимия. 2017. Т. 53. С. 1212. [Martemianov, S.A., Statistical Theory of Turbulent Mass Transfer in Electrochemical Systems, Russ. J. Electrochem., 2017, vol. 53, p. 1076.]
Мартемьянов, С.А., Воротынцев, M.В., Графов, Б.M., Вывод нелокального уравнения массопереноса в турбулентном диффузионном слое. Электрохимия. 1979. Т. 15. № 6. С. 766. [Martem’yanov, S.A., Vorotyntsev, M.A., and Grafov, B.M., Derivation of the Nonlocal Transport Equation of Matter in the Turbulent Diffusion Layer, Soviet Electrochem., 1979, vol. 15, no. 6, p. 787.]
Дополнительные материалы отсутствуют.