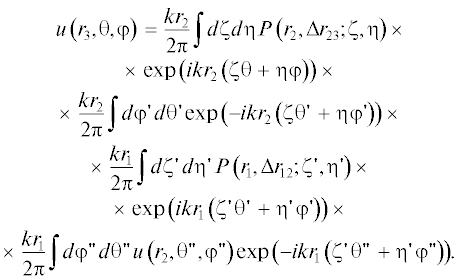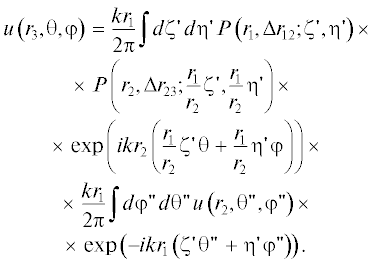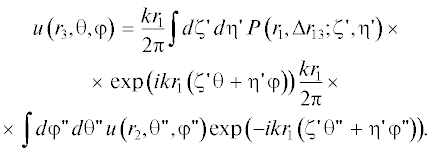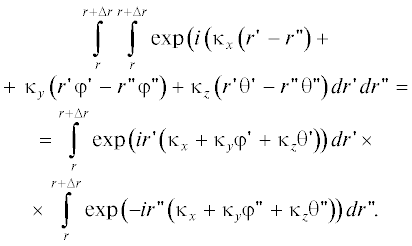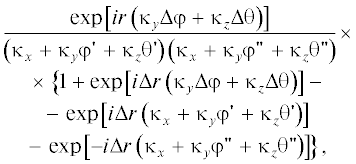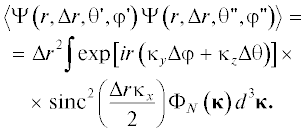Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 1, стр. 66-75
Метод сферических фазовых экранов для моделирования расходящихся волновых пучков в неоднородных средах
М. Е. Горбунов a, b, *, О. А. Коваль a, А. Е. Мамонтов a
a Институт физики атмосферы им. А.М. Обухова РАН
119017 Москва, Пыжевский пер., 3, Россия
b ФГБУ “Гидрометцентр России”
123242 Москва, Большой Предтеченский переулок, д. 11–13, Россия
* E-mail: gorbunov@ifaran.ru
Поступила в редакцию 27.06.2019
После доработки 06.08.2019
Принята к публикации 25.09.2019
Аннотация
Метод фазовых экранов широко применяется для моделирования распространения волн в неоднородных средах. Чаще всего применяется метод плоских фазовых экранов. Однако для моделирования 2-мерной задачи радиозатменного зондирования атмосферы ранее был разработан метод цилиндрических фазовых экранов. В данной работе мы строим дальнейшее обобщение этого метода для 3-мерной задачи и предлагаем метод сферических фазовых экранов. В малоугловом приближении мы получаем формулу для вакуумного пропагатора, описывающего распространение волны с экрана на экран. Мы получаем также выражение для спектра флуктуаций фазового набега в тонком сферическом слое изотропной случайной среды. Мы описываем численную реализацию метода и приводим результаты численного моделирования распространения расходящегося лазерного пучка на атмосферной трассе длиной 25 км.
ВВЕДЕНИЕ
Метод фазовых экранов давно и широко применяется для численного моделирования распространения волн различной природы в неоднородных средах. В качестве примеров укажем задачи моделирования распространения оптического (лазерного) излучения в турбулентной атмосфере [1–5], задачи моделирования распространения дециметровых волн при радиозатменном зондировании атмосферы [6–8]. Этот метод в англоязычной литературе называется split-step, метод пошагового расщепления. Соответственно в русскоязычной литературе используется название “метод расщепления по физическим параметрам”. Это название отражает тот факт, что неоднородная среда в этом методе представляется как последовательность тонких слоев, а пропагатор, описывающий распространение волны через каждый слой, приближенно записывается как композиция бесконечно тонкого слоя, формирующего фазовые искажения волны, и вакуумного пропагатора, описывающего дифракцию.
Принципиальное ограничение метода фазовых экранов состоит в том, что он не учитывает рассеяния назад. Метод фазовых экранов можно также рассматривать как конечномерную аппроксимацию континуального интеграла, описывающего распространения волны в неоднородной среде [9].
В задачах моделирования лазерного излучения в турбулентных средах, особенно для описания эффекта изотропной турбулентности, применяются 2-мерные фазовые экраны. Однако в задачах моделирования радиозатменных экспериментов существенная оптимизация вычислительных затрат достигается за счет использования одномерных фазовых экранов. Это связано с тем, что в большинстве случаев здесь учитываются атмосферные неоднородности с вертикальными масштабами от сотен метров до километров, горизонтальные масштабы которых существенно превышают горизонтальный размер зоны Френеля.
В классическом варианте метода используются плоские фазовые экраны. Этот приводит к излишним затратам вычислительных ресурсов в случае описания расходящейся волны, поскольку на краях каждого экрана угол между экраном и волновым фронтом увеличивается, что приводит к необходимости уменьшения шага дискретизации. В 2-мерном моделировании радиозатменных экспериментов оказалось достаточно просто записать решение для цилиндрических 1-мерных фазовых экранов [7], позволяющее учесть форму фазового фронта падающей волны.
В настоящей работе мы строим обобщение этого подхода и развиваем метод сферических фазовых экранов. Поскольку простого точного решения в этом случае получить не удается, мы используем малоугловое приближение. В разделе Вывод основных соотношений мы, пользуясь техникой угловых спектров [10], выводим формулу для пропагатора в сферических координатах в малоугловом приближении. В разделе Численное моделирование мы показываем, что численная реализация этого метода не сложнее случая плоских фазовых экранов, и приводим примеры численного моделирования с использованием модели изотропной турбулентности.
ВЫВОД ОСНОВНЫХ СООТНОШЕНИЙ. ВАКУУМНЫЙ ПРОПАГАТОР
В качестве примера мы будем использовать параметры пучка, заданные для проекта DELICAT (DEmonstration of LIdar based Clear Air Turbulence detection, Демонстрация обнаружения турбулентности ясного неба при помощи лидара) [11, 12]: длина волны λ = 354.84 нм, расходимость $2\alpha = 0.3$ мрад. Сам излагаемый метод может применяться и при других параметрах пучка, в рамках условий применимости используемого приближения.
Будем рассматривать декартовы координаты $\left( {x,y,z} \right)$ и сферические координаты $\left( {r,\theta ,\varphi } \right)$, связанные между собой следующим образом:
(1)
$\begin{gathered} x = r\cos \theta \cos \varphi ,\,\,\,\,y = r\cos \theta \sin \varphi , \\ z = r\sin \theta . \\ \end{gathered} $Рассмотрим волновое поле в пространстве $u\left( {x,y,z} \right)$ с наложенным условием излучения, выделяющим волны, распространяющиеся в направлении оси $x$. Пусть для волнового поля задано граничное условие ${{u}_{0}}\left( {y,z} \right)$ в плоскости $x = 0.$ Будем пользоваться преобразованием Фурье в следующей нормировке:
(2)
$\begin{gathered} \tilde {f}\left( {\eta ,\zeta } \right) = \frac{k}{{2\pi }}\int {f\left( {y,z} \right)\exp \left( {ik\eta y + ik\zeta z} \right)dydz} , \\ f\left( {y,z} \right) = \frac{k}{{2\pi }}\int {\tilde {f}\left( {\eta ,\zeta } \right)\exp \left( {ik\eta y + ik\zeta z} \right)d\eta d\zeta ,} \\ \end{gathered} $(3)
$\begin{gathered} u\left( {r,\theta ,\varphi } \right) = \frac{k}{{2\pi }} \times \\ \times \,\,\int {\widetilde {{{u}_{0}}}\left( {\eta ,\zeta } \right)\exp \left[ {ikS\left( {r,\theta ,\varphi ;\eta ,\zeta } \right)} \right]d\eta d\zeta } , \\ \end{gathered} $(4)
$\begin{gathered} S\left( {r,\theta ,\varphi ;\eta ,\zeta } \right) = r(\sqrt {1 - {{\eta }^{2}} - {{\zeta }^{2}}} \cos \theta \cos \varphi + \\ + \,\,\eta \cos \theta \sin \varphi + \zeta \sin \theta ). \\ \end{gathered} $Максимальные абсолютные значения $\eta $, $\zeta $, $\theta $ и $\varphi $ оцениваются величиной половинной расходимости пучка α = 0.15 × 10−3. Расстояние распространения $r$ оценивается величиной 30 км. В дальнейшем мы будем пользоваться малоугловым разложением фазовой функции, поэтому оценим, члены каких степеней следует удерживать:
(5)
$\begin{gathered} kr\alpha = 7.96819 \times {{10}^{7}},\,\,\,\,kr{{\alpha }^{2}} = {\text{11952}}{\text{.3,}} \\ kr{{\alpha }^{3}} = {\text{1}}{\text{.79284,}}\,\,\,\,kr{{\alpha }^{4}} = {\text{0}}{\text{.000268926}}{\text{.}} \\ \end{gathered} $Таким образом, в разложениях следует удерживать члены до 3-го порядка включительно. Однако фактически члены 3-го порядка в разложениях отсутствуют, поэтому достаточно учесть члены 2-го порядка. Это позволяет записать следующее приближенное выражение для фазовой функции:
(6)
$\begin{gathered} S\left( {r,\theta ,\varphi ;\eta ,\zeta } \right) = \\ = r\left( {\left( {1 - \frac{{{{\eta }^{2}} + {{\zeta }^{2}}}}{2} - \frac{{{{\theta }^{2}} + {{\varphi }^{2}}}}{2}} \right) + \eta \varphi + \zeta \theta } \right). \\ \end{gathered} $Пользуясь этим приближением, запишем поле в пространстве в виде преобразования Фурье:
(7)
$\begin{gathered} u\left( {r,\theta ,\varphi } \right) = \exp \left[ {ikr\left( {1 - \frac{{{{\theta }^{2}} + {{\varphi }^{2}}}}{2}} \right)} \right] \times \\ \times \,\,\frac{k}{{2\pi }}\int {\widetilde {{{u}_{0}}}\left( {\eta ,\zeta } \right)\exp \left( { - ikr\frac{{{{\eta }^{2}} + {{\zeta }^{2}}}}{2}} \right)} \times \\ \times \,\,\exp \left( {ikr\left( {\eta \varphi + \zeta \theta } \right)} \right)d\eta d\zeta . \\ \end{gathered} $Для численного нахождения поля в неоднородной среде будем применять метод фазовых экранов. В рамках этого метода каждый экран будем считать участком сферы с некоторым (текущим) радиусом $r$. Будем вычислять поле на следующем экране с радиусом $r + \Delta r$, пользуясь вакуумным пропагатором и умножая полученное поле на множитель, приближенно учитывающий среду. Для вакуумного пропагатора несложно получить явное выражение. Для этого, пользуясь полем на исходном экране, будем вычислять эффективный пространственный спектр $\widetilde {{{u}_{0}}}\left( {r,\eta ,\zeta } \right)$:
(8)
$\begin{gathered} \widetilde {{{u}_{0}}}\left( {r,\eta ,\zeta } \right) = \exp \left( {ikr\frac{{{{\eta }^{2}} + {{\zeta }^{2}}}}{2}} \right) \times \\ \times \,\,\frac{{kr}}{{2\pi }}\int {u\left( {r,\theta ,\varphi } \right)\exp \left[ { - ikr\left( {1 - \frac{{{{\theta }^{2}} + {{\varphi }^{2}}}}{2}} \right)} \right]} \times \\ \times \,\,\exp \left( { - ikr\left( {\eta \varphi + \zeta \theta } \right)} \right)d\varphi d\theta . \\ \end{gathered} $Эффективный спектр равен тому пространственному спектру поля в плоскости $x = 0,$ при котором на данном фазовом экране в отсутствие среды формировалось бы поле $u\left( {r,\theta ,\varphi } \right).$ Далее, пользуясь формулой (7) с подстановкой $r + \Delta r$ и $\widetilde {{{u}_{0}}}\left( {r,\eta ,\zeta } \right),$ и учитывая влияние среды, мы получаем поле на следующем экране:
(9)
$\begin{gathered} u\left( {r + \Delta r,\theta ,\varphi } \right) = \exp \left( {ik\Psi \left( {r,r + \Delta r,\theta ,\varphi } \right)} \right) \times \\ \times \,\,\exp \left[ {ik\left( {r + \Delta r} \right)\left( {1 - \frac{{{{\theta }^{2}} + {{\varphi }^{2}}}}{2}} \right)} \right] \times \\ \times \,\,\frac{k}{{2\pi }}\int {\widetilde {{{u}_{0}}}\left( {r,\eta ,\zeta } \right)\exp \left( { - ik\left( {r + \Delta r} \right)\frac{{{{\eta }^{2}} + {{\zeta }^{2}}}}{2}} \right)} \times \\ \times \,\,\exp \left( {ik\left( {r + \Delta r} \right)\left( {\eta \varphi + \zeta \theta } \right)} \right)d\eta d\zeta , \\ \end{gathered} $Перепишем формулу (8) в следующей форме:
(10)
$\begin{gathered} \widetilde {{{u}_{0}}}\left( {r,\eta ,\zeta } \right) = \exp \left( { - ikr} \right)\frac{{k{{r}^{2}}}}{{2\pi }} \times \\ \times \,\,\int {u\left( {r,\theta ,\varphi } \right)\exp \left[ {\frac{{ikr}}{2}\left( {{{{\left( {\theta - \zeta } \right)}}^{2}} + {{{\left( {\varphi - \eta } \right)}}^{2}}} \right)} \right]d\varphi d\theta } . \\ \end{gathered} $Тогда поле на следующем фазовом экране можно записать аналогично:
(11)
$\begin{gathered} u\left( {r + \Delta r,\theta ,\varphi } \right) = \\ = \exp \left( {ik\left( {\left( {r + \Delta r} \right) + \Psi \left( {r,\Delta r,\theta ,\varphi } \right)} \right)} \right) \times \\ \times \,\,\frac{k}{{2\pi }}\int {\widetilde {{{u}_{0}}}\left( {r,\eta ,\zeta } \right)} \times \\ \times \,\,\exp \left( {\frac{{ - ik\left( {r + \Delta r} \right)}}{2}\left( {{{{\left( {\theta - \zeta } \right)}}^{2}} + {{{\left( {\varphi - \eta } \right)}}^{2}}} \right)} \right)d\eta d\zeta . \\ \end{gathered} $Подставляя сюда формулу (10), получаем:
(12)
$\begin{gathered} u\left( {r + \Delta r,\theta ,\varphi } \right) = \exp \left( {ik\left( {\Delta r + \Psi \left( {r,\Delta r,\theta ,\varphi } \right)} \right)} \right) \times \\ \times \,\,\frac{{{{k}^{2}}{{r}^{2}}}}{{4{{\pi }^{2}}}}\int {\exp \left( {\frac{{ - ik\left( {r + \Delta r} \right)}}{2}\left( {{{{\left( {\theta - \zeta } \right)}}^{2}} + {{{\left( {\varphi - \eta } \right)}}^{2}}} \right)} \right)} \times \\ \times \,\,\int {u\left( {r,\theta {\kern 1pt} ',\varphi {\kern 1pt} '} \right)} \times \\ \times \,\,\exp \left[ {\frac{{ikr}}{2}\left( {{{{\left( {\theta {\kern 1pt} ' - \zeta } \right)}}^{2}} + {{{\left( {\varphi {\kern 1pt} ' - \eta } \right)}}^{2}}} \right)} \right]d\varphi {\kern 1pt} 'd\theta {\kern 1pt} 'd\eta d\zeta . \\ \end{gathered} $Выделим здесь интегрирование по промежуточным переменным $\eta ,\zeta $:
(13)
$\begin{gathered} u\left( {r + \Delta r,\theta ,\varphi } \right) = \exp \left( {ik\left( {\Delta r + \Psi \left( {r,\Delta r,\theta ,\varphi } \right)} \right)} \right) \times \\ \times \,\,\frac{{{{k}^{2}}{{r}^{2}}}}{{4{{\pi }^{2}}}}\int {d\varphi {\kern 1pt} 'd\theta {\kern 1pt} 'u\left( {r,\theta {\kern 1pt} ',\varphi {\kern 1pt} '} \right)} \times \\ \times \,\,\int {\exp \left[ {\frac{{ - ik\left( {r + \Delta r} \right)}}{2}{{{\left( {\theta - \zeta } \right)}}^{2}} + \frac{{ikr}}{2}{{{\left( {\theta {\kern 1pt} '\,\, - \zeta } \right)}}^{2}}} \right]d\zeta } \times \\ \times \,\,\int {\exp \left[ {\frac{{ - ik\left( {r + \Delta r} \right)}}{2}{{{\left( {\varphi - \eta } \right)}}^{2}} + \frac{{ikr}}{2}{{{\left( {\varphi {\kern 1pt} '\,\, - \eta } \right)}}^{2}}} \right]d\eta .} \\ \end{gathered} $Выполняя интегрирование по $\eta $ и $\zeta $, получаем:
(14)
$\begin{gathered} u\left( {r + \Delta r,\theta ,\varphi } \right) = \exp \left( {ik\left( {\Delta r + \Psi \left( {r,\Delta r,\theta ,\varphi } \right)} \right)} \right) \times \\ \times \,\,\frac{{{{k}^{2}}{{r}^{2}}}}{{4{{\pi }^{2}}}}\int {d\varphi {\kern 1pt} 'd\theta {\kern 1pt} 'u\left( {r,\theta {\kern 1pt} ',\varphi {\kern 1pt} '} \right)} \times \\ \times \,\,\frac{{2\pi }}{{ik\Delta r}}\exp \left( {\frac{{ikr\left( {r + \Delta r} \right)}}{{2\Delta r}}\left[ {{{{\left( {\theta - \theta {\kern 1pt} '} \right)}}^{2}} + {{{\left( {\varphi - \varphi {\kern 1pt} '} \right)}}^{2}}} \right]} \right). \\ \end{gathered} $Вычисляя этот интеграл для сферической волны $u\left( {r,\theta {\kern 1pt} ',\varphi {\kern 1pt} '} \right) = \operatorname{const} ,$ получим:
(15)
$\begin{gathered} u\left( {r + \Delta r,\theta ,\varphi } \right) = \exp \left( {ik\left( {\Delta r + \Psi \left( {r,\Delta r,\theta ,\varphi } \right)} \right)} \right) \times \\ \times \,\,u\left( {r,\theta ,\varphi } \right)\frac{{{{k}^{2}}{{r}^{2}}}}{{2\pi ik\Delta r}}\frac{{2\pi \Delta r}}{{ - ikr\left( {r + \Delta r} \right)}} = \\ = \exp \left( {ik\left( {\Delta r + \Psi \left( {r,\Delta r,\theta ,\varphi } \right)} \right)} \right)u\left( {r,\theta ,\varphi } \right)\frac{r}{{r + \Delta r}}. \\ \end{gathered} $Пользуясь представлением:
(16)
$\begin{gathered} \exp \left( {\frac{{ikr\left( {r + \Delta r} \right)}}{{2\Delta r}}\left[ {{{{\left( {\theta - \theta {\kern 1pt} '} \right)}}^{2}} + {{{\left( {\varphi - \varphi '} \right)}}^{2}}} \right]} \right) = \\ = \frac{{ikr\Delta r}}{{2\pi \left( {r + \Delta r} \right)}}\int {\exp \left( {\frac{{ - ikr\Delta r}}{{2\left( {r + \Delta r} \right)}}\left( {{{\zeta }^{2}} + {{\eta }^{2}}} \right)} \right)} \times \\ \times \,\,\exp \left( {ikr\left( {\zeta \left( {\theta - \theta {\kern 1pt} '} \right) + \eta \left( {\varphi - \varphi {\kern 1pt} '} \right)} \right)} \right)d\zeta d\eta , \\ \end{gathered} $(17)
$\begin{gathered} u\left( {r + \Delta r,\theta ,\varphi } \right) = \exp \left( {ik\Psi \left( {r,\Delta r,\theta ,\varphi } \right)} \right) \times \\ \times \,\,\frac{{kr}}{{2\pi }}\int {d\zeta d\eta P\left( {r,\Delta r;\zeta ,\eta } \right)\exp \left( {ikr\left( {\zeta \theta + \eta \varphi } \right)} \right)} \times \\ \times \,\,\frac{{kr}}{{2\pi }}\int {u\left( {r,\theta {\kern 1pt} ',\varphi {\kern 1pt} '} \right)\exp \left( { - ikr\left( {\zeta \theta {\kern 1pt} '\,\, + \eta \varphi {\kern 1pt} '} \right)} \right)d\varphi {\kern 1pt} 'd\theta {\kern 1pt} '} , \\ \end{gathered} $(18)
$\begin{gathered} P\left( {r,\Delta r;\zeta ,\eta } \right) = \frac{r}{{r + \Delta r}} \times \\ \times \,\,\exp \left( {ik\Delta r\left( {1 - \frac{r}{{2\left( {r + \Delta r} \right)}}\left( {{{\zeta }^{2}} + {{\eta }^{2}}} \right)} \right)} \right). \\ \end{gathered} $Это представление соответствует стандартному методу фазовых экранов (split-step). Пересчет поля с экрана на экран выполняется в три шага. На первом шаге вычисляется пространственный спектр поля в исходном фазовом экране. На втором шаге спектр умножается на вакуумный пропагатор и при помощи обратного преобразования Фурье вычисляется поле на следующем фазовом экране без учета среды. На третьем шаге это поле умножается на фазовый множитель, учитывающий фазовый набег в среде между экранами.
Множитель $\exp \left( {ik\Delta r} \right)$ можно опустить, поскольку он дает постоянную добавку к фазе в каждом экране. В этом случае вакуумный пропагатор можно записать в следующем виде:
(19)
$P\left( {r,\Delta r;\zeta ,\eta } \right) = \frac{r}{{r + \Delta r}}\exp \left( {\frac{{ - ikr\Delta r}}{{2\left( {r + \Delta r} \right)}}\left( {{{\zeta }^{2}} + {{\eta }^{2}}} \right)} \right).$Перепишем формулу (17) в операторном виде:
(20)
$u\left( {r + \Delta r,\theta ,\varphi } \right) = \hat {P}\left( {r,\Delta r} \right)u\left( {r,\theta {\kern 1pt} ',\varphi {\kern 1pt} '} \right),$Выделим здесь интегрирование по $d\varphi {\kern 1pt} 'd\theta {\kern 1pt} '$:
Вычисляя внутренний интеграл по $d\varphi {\kern 1pt} 'd\theta {\kern 1pt} '$, получаем:
(23)
$\begin{gathered} {{\left( {\frac{{k{{r}_{2}}}}{{2\pi }}} \right)}^{2}}\int {d\varphi {\kern 1pt} 'd\theta {\kern 1pt} '} \times \\ \times \,\,\exp \left( { - ik{{r}_{2}}\left( {\left( {\zeta - \frac{{{{r}_{1}}}}{{{{r}_{2}}}}\zeta {\kern 1pt} '} \right)\theta {\kern 1pt} ' + \left( {\eta - \frac{{{{r}_{1}}}}{{{{r}_{2}}}}\eta {\kern 1pt} '} \right)\varphi {\kern 1pt} '} \right)} \right) = \\ = \delta \left( {\zeta - \frac{{{{r}_{1}}}}{{{{r}_{2}}}}\zeta {\kern 1pt} '} \right)\delta \left( {\eta - \frac{{{{r}_{1}}}}{{{{r}_{2}}}}\eta {\kern 1pt} '} \right). \\ \end{gathered} $Это позволяет переписать интеграл (22) следующим образом:
Выполняя интегрирование по $d\zeta d\eta ,$ и учитывая стандартное свойство $\delta {\text{ - }}$функции, получаем:
Рассмотрим выражение $P\left( {{{r}_{1}},\Delta {{r}_{{12}}};\zeta {\kern 1pt} ',\eta {\kern 1pt} '} \right)$ × $ \times \,\,P\left( {{{r}_{2}},\Delta {{r}_{{23}}};\frac{{{{r}_{1}}}}{{{{r}_{2}}}}\zeta {\kern 1pt} ',\frac{{{{r}_{1}}}}{{{{r}_{2}}}}\eta {\kern 1pt} '} \right)$:
(26)
$\begin{gathered} P\left( {{{r}_{1}},\Delta {{r}_{{12}}};\zeta {\kern 1pt} ',\eta {\kern 1pt} '} \right)P\left( {{{r}_{2}},\Delta {{r}_{{23}}};\frac{{{{r}_{1}}}}{{{{r}_{2}}}}\zeta {\kern 1pt} ',\frac{{{{r}_{1}}}}{{{{r}_{2}}}}\eta {\kern 1pt} '} \right) = \\ = \frac{{{{r}_{1}}}}{{{{r}_{2}}}}\exp \left( {\frac{{ - ik{{r}_{1}}\Delta {{r}_{{12}}}}}{{2{{r}_{2}}}}\left( {\zeta {\kern 1pt} {{'}^{2}} + \eta {\kern 1pt} {{'}^{2}}} \right)} \right)\frac{{{{r}_{2}}}}{{{{r}_{3}}}} \times \\ \times \,\,\exp \left( {\frac{{ - ik{{r}_{2}}\Delta {{r}_{{23}}}}}{{2{{r}_{3}}}}{{{\left( {\frac{{{{r}_{1}}}}{{{{r}_{2}}}}} \right)}}^{2}}\left( {{{{\zeta '}}^{2}} + \eta {\kern 1pt} {{'}^{2}}} \right)} \right) = \\ = \frac{{{{r}_{1}}}}{{{{r}_{3}}}}\exp \left( {\frac{{ - ik}}{2}\left( {\frac{{{{r}_{1}}\Delta {{r}_{{12}}}}}{{{{r}_{2}}}} + \frac{{{{r}_{2}}\Delta {{r}_{{23}}}}}{{{{r}_{3}}}}{{{\left( {\frac{{{{r}_{1}}}}{{{{r}_{2}}}}} \right)}}^{2}}} \right)\left( {\zeta {\kern 1pt} {{'}^{2}} + \eta {\kern 1pt} {{'}^{2}}} \right)} \right) = \\ = \frac{{{{r}_{1}}}}{{{{r}_{3}}}}\exp \left( {\frac{{ - ik{{r}_{1}}\Delta {{r}_{{13}}}}}{{2{{r}_{3}}}}\left( {\zeta {\kern 1pt} {{'}^{2}} + \eta {\kern 1pt} {{'}^{2}}} \right)} \right), \\ \end{gathered} $Этим доказано естественное групповое свойство вакуумных операторов $\hat {P}\left( {r,\Delta r} \right)$:
(28)
$\hat {P}\left( {{{r}_{2}},\Delta {{r}_{{23}}}} \right) \circ \hat {P}\left( {{{r}_{1}},\Delta {{r}_{{12}}}} \right) = \hat {P}\left( {{{r}_{1}},\Delta {{r}_{{13}}}} \right).$Из точности группового свойства следует, что данный пропагатор является точным решением приближенной формы параболического уравнения, в котором в качестве поперечных координат используются ${y \mathord{\left/ {\vphantom {y r}} \right. \kern-0em} r}$ и ${z \mathord{\left/ {\vphantom {z r}} \right. \kern-0em} r},$ а также учтено регулярное убывание амплитуды сферической волны как ${1 \mathord{\left/ {\vphantom {1 r}} \right. \kern-0em} r}.$ Альтернативный подход к учету расходимости волны возможен с использованием линзовых координат [13–15]. Тем не менее в указанной литературе линзовые координаты применяются для описания пучков в однородной нелинейной диспергирующей среде. Возможность применения этого преобразования к произвольной неоднородной среде требует дополнительного исследования.
Метод сферических фазовых экранов может также применяться для исследования сфокусированных пучков, в том числе в условиях самофокусировки. Пропагатор (18) при $\Delta r < 0$ описывает не расходящийся, а сходящийся пучок.
ФАЗОВЫЙ НАБЕГ В ТОНКОМ СФЕРИЧЕСКОМ СЛОЕ
Каждый слой случайно-неоднородной среды толщиной $\Delta r$ между фазовыми экранами $r$ и $r + \Delta r$ описывается функцией $\Psi \left( {r,\Delta r,\theta ,\varphi } \right),$ которая понимается как реализация 2-мерного случайного поля как функция от $\theta ,\varphi $ при заданных $r$ и $\Delta r$. Рассмотрим соответствующую реализацию 3-мерного поля индекса рефракции $N\left( {x,y,z} \right)$. Тогда можно записать:
(29)
$\begin{gathered} \Psi \left( {r,\Delta r,\theta ,\varphi } \right) = \\ = \int\limits_r^{r + \Delta r} {N\left( {r\cos \theta \cos \varphi ,r\cos \theta \sin \varphi ,r\sin \theta } \right)dr} . \\ \end{gathered} $Будем пользоваться для вычисления этой функции малоугловым приближением. Поскольку $r{{\alpha }^{2}}$ = 0.675 мм, то величинами 2-го порядка можно пренебрегать. Таким образом, можно записать следующее приближенное выражение:
(30)
$\Psi \left( {r,\Delta r,\theta ,\varphi } \right) = \int\limits_r^{r + \Delta r} {N\left( {r,r\varphi ,r\theta } \right)dr} .$Мы будем пренебрегать регулярной частью индекса рефракции, считая его константой, дающей в каждом экране некоторый известный несущественный постоянный фазовый сдвиг. Поле $N\left( {x,y,z} \right)$ будет считаться трехмерным статистически однородным и изотропным случайным полем со спектральной плотностью ${{\Phi }_{N}}\left( {\mathbf{\kappa }} \right) = {{\Phi }_{N}}\left( \kappa \right),$ где ${\mathbf{\kappa }} = \left( {{{\kappa }_{x}},{{\kappa }_{y}},{{\kappa }_{z}}} \right)$ – трехмерный вектор пространственных частот, $\kappa = \left| {\mathbf{\kappa }} \right|$. Для корреляционной функции имеет место стандартное соотношение:
(31)
$\left\langle {N\left( {{{{\mathbf{r}}}_{1}}} \right)N{\text{*}}\left( {{{{\mathbf{r}}}_{2}}} \right)} \right\rangle = \int {\exp \left( {i\kappa \left( {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}} \right)} \right){{\Phi }_{N}}\left( \kappa \right){{d}^{3}}\kappa } .$Рассмотрим корреляции фазового пути:
Выделим здесь интегрирование по  :
:
Этот интеграл равен:
где мы ввели обозначения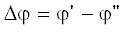 и
и 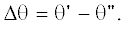 Эта величина не является функцией от $\Delta \varphi $ и $\Delta \theta $. Однако в малоугловом приближении поправки, включающие ${{\kappa }_{y}}\varphi {\kern 1pt} '\,\, + {{\kappa }_{z}}\theta {\kern 1pt} '$ и
Эта величина не является функцией от $\Delta \varphi $ и $\Delta \theta $. Однако в малоугловом приближении поправки, включающие ${{\kappa }_{y}}\varphi {\kern 1pt} '\,\, + {{\kappa }_{z}}\theta {\kern 1pt} '$ и  либо не в виде разностей, либо с множителем $\Delta r$, как в числителе, так и в знаменателе можно приближенно исключить. При этом $\Delta r$ считается малым по сравнению с $r$. Тогда выражение (34) можно переписать в следующей приближенной форме:
либо не в виде разностей, либо с множителем $\Delta r$, как в числителе, так и в знаменателе можно приближенно исключить. При этом $\Delta r$ считается малым по сравнению с $r$. Тогда выражение (34) можно переписать в следующей приближенной форме:
(35)
$\begin{gathered} \exp \left[ {ir\left( {{{\kappa }_{y}}\Delta \varphi + {{\kappa }_{z}}\Delta \theta } \right)} \right]\frac{{2\left[ {1 - \cos \left( {\Delta r{{\kappa }_{x}}} \right)} \right]}}{{\kappa _{x}^{2}}} = \\ = \exp \left[ {ir\left( {{{\kappa }_{y}}\Delta \varphi + {{\kappa }_{z}}\Delta \theta } \right)} \right]\frac{{4{{{\sin }}^{2}}\left( {\frac{{\Delta r{{\kappa }_{x}}}}{2}} \right)}}{{\kappa _{x}^{2}}}. \\ \end{gathered} $Пользуясь функцией $\operatorname{sinc} x = {{\sin x} \mathord{\left/ {\vphantom {{\sin x} x}} \right. \kern-0em} x}$, это выражение можно переписать в следующей форме:
(36)
$\Delta {{r}^{2}}\exp \left[ {ir\left( {{{\kappa }_{y}}\Delta \varphi + {{\kappa }_{z}}\Delta \theta } \right)} \right]{{\operatorname{sinc} }^{2}}\left( {\frac{{\Delta r{{\kappa }_{x}}}}{2}} \right).$Это позволяет преобразовать интеграл (32) следующим образом:
Получим выражение для спектральной плотности фазового пути ${{\Phi }_{\Psi }}\left( \mu \right)$, где ${\mathbf{\mu }} = \left( {{{\mu }_{\varphi }},{{\mu }_{\theta }}} \right)$ – вектор пространственных частот. Имеет место следующее соотношение:
Если положить ${{\mu }_{\varphi }} = r{{\kappa }_{y}}$ и ${{\mu }_{\theta }} = r{{\kappa }_{z}},$ то мы придем к следующему выражению для спектральной плотности фазового пути:
(39)
${{\Phi }_{\Psi }}\left( {\mathbf{\mu }} \right) = \frac{{\Delta {{r}^{2}}}}{{{{r}^{2}}}}\int {{{{\operatorname{sinc} }}^{2}}\left( {\frac{{\Delta r{{\kappa }_{x}}}}{2}} \right){{\Phi }_{N}}\left( {{{\kappa }_{x}},\frac{{{{\mu }_{\varphi }}}}{r},\frac{{{{\mu }_{\theta }}}}{r}} \right)d{{\kappa }_{x}}} .$Эта формула записана в приближении тонкого слоя среды, поэтому она не учитывает то, что в силу уширения пучка в угловые частоты ${\mathbf{\mu }}$ дают вклад не только поперечные частоты ${{\mathbf{\mu }} \mathord{\left/ {\vphantom {{\mathbf{\mu }} r}} \right. \kern-0em} r}.$ Для слоя среды толщиной порядка внешнего масштаба неоднородностей и более можно записать по аналогии с соответствующей формулой для плоского слоя [1, 2]:
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
Для турбулентных флуктуаций индекса рефракции мы примем в качестве модели колмогоровско-кармановский спектр:
(41)
${{\Phi }_{N}}(\kappa ) = 0.033C_{n}^{2}{{\left( {{{\kappa }^{2}} + \kappa _{0}^{2}} \right)}^{{ - 11/6}}}\exp \left( {{{ - {{\kappa }^{2}}} \mathord{\left/ {\vphantom {{ - {{\kappa }^{2}}} {\kappa _{m}^{2}}}} \right. \kern-0em} {\kappa _{m}^{2}}}} \right),$Численный алгоритм аналогичен случаю плоских фазовых экранов. Поскольку вакуумный пропагатор (19) записан как мультипликатор в пространстве Фурье-образов поля, его численная реализация сводится к выполнению быстрого преобразования Фурье, умножению на пропагатор и обратному преобразованию Фурье.
Для генерации реализаций случайных некоррелированных фазовых экранов мы пользуемся дискретной формой соотношения (38) [16]:
(42)
$\begin{gathered} \Phi _{{jl}}^{{\left( \Psi \right)}} = \frac{{{{{\left( {\Delta \varphi \Delta \theta } \right)}}^{2}}}}{{4{{\pi }^{2}}{{N}_{\varphi }}\Delta \varphi {{N}_{\theta }}\Delta \theta }} \times \\ \times \,\,\left\langle {{{{\left| {\sum\limits_{j'l'} {{{\Psi }_{{j'l'}}}\exp \left( { - i\frac{{2\pi jj{\kern 1pt} '}}{{{{N}_{\varphi }}}} - i\frac{{2\pi ll{\kern 1pt} '}}{{{{N}_{\theta }}}}} \right)} } \right|}}^{2}}} \right\rangle = \\ = \frac{{\Delta \varphi \Delta \theta }}{{4{{\pi }^{2}}{{N}_{\varphi }}{{N}_{\theta }}}}\left\langle {{{{\left| {{{{\tilde {\Psi }}}_{{jl}}}} \right|}}^{2}}} \right\rangle , \\ \end{gathered} $(43)
${{\tilde {\Psi }}_{{jl}}} = \sum\limits_{j'l'} {{{\Psi }_{{j'l'}}}\exp \left( { - i\frac{{2\pi jj{\kern 1pt} '}}{{{{N}_{\varphi }}}} - i\frac{{2\pi ll{\kern 1pt} '}}{{{{N}_{\theta }}}}} \right)} .$Таким образом, ${{\tilde {\Psi }}_{{jl}}}$ являются некоррелированными случайными величинами со случайными фазами и среднеквадратичными значениями:
(44)
$\left\langle {{{{\left| {{{{\tilde {\Psi }}}_{{jl}}}} \right|}}^{2}}} \right\rangle = \Phi _{{jl}}^{{\left( \Psi \right)}}\frac{{4{{\pi }^{2}}{{N}_{\varphi }}{{N}_{\theta }}}}{{\Delta \varphi \Delta \theta }}.$Для генерации случайной реализации ${{\tilde {\Psi }}_{{jl}}}$ рассмотрим независимые случайные величины $\xi _{{jl}}^{{(1)}}$ и $\xi _{{jl}}^{{(2)}}$, равномерно распределенные в интервале [0, 1]. Тогда реализация ${{\tilde {\Psi }}_{{jl}}}$ дается формулой:
(45)
${{\tilde {\Psi }}_{{jl}}} = 2\pi \sqrt {\Phi _{{jl}}^{{\left( \Psi \right)}}\frac{{{{N}_{\varphi }}{{N}_{\theta }}}}{{\Delta \varphi \Delta \theta }}} \sqrt { - \ln \xi _{{jl}}^{{(1)}}} \exp \left( {2\pi i\xi _{{jl}}^{{(2)}}} \right),$(46)
$\begin{gathered} {{{\tilde {\Psi }}}_{{jl}}} = 2\pi \sqrt {\frac{{2\pi \Delta r}}{{{{r}^{2}}}}{{\Phi }_{N}}\left( {0,\frac{{\mu _{j}^{\varphi }}}{r},\frac{{\mu _{l}^{\theta }}}{r}} \right)\frac{{{{N}_{\varphi }}{{N}_{\theta }}}}{{\Delta \varphi \Delta \theta }}} \times \\ \times \,\,\sqrt { - \ln \xi _{{jl}}^{{(1)}}} \exp \left( {2\pi i\xi _{{jl}}^{{(2)}}} \right), \\ \end{gathered} $(47)
$\begin{gathered} {{\Phi }_{N}}\left( {0,\frac{{\mu _{j}^{\varphi }}}{r},\frac{{\mu _{l}^{\theta }}}{r}} \right) = \\ = 0.033C_{n}^{2}{{\left( {{{{\left( {\frac{{\mu _{j}^{\varphi }}}{r}} \right)}}^{2}} + {{{\left( {\frac{{\mu _{l}^{\theta }}}{r}} \right)}}^{2}} + \kappa _{0}^{2}} \right)}^{{ - 11/6}}} \times \\ \times \,\,\exp \left( { - {{\left( {{{{\left( {\frac{{\mu _{j}^{\varphi }}}{r}} \right)}}^{2}} + {{{\left( {\frac{{\mu _{l}^{\theta }}}{r}} \right)}}^{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\left( {\frac{{\mu _{j}^{\varphi }}}{r}} \right)}}^{2}} + {{{\left( {\frac{{\mu _{l}^{\theta }}}{r}} \right)}}^{2}}} \right)} {\kappa _{m}^{2}}}} \right. \kern-0em} {\kappa _{m}^{2}}}} \right). \\ \end{gathered} $Реализация оптической толщины экрана ${{\Psi }_{{jl}}}$ равна обратному дискретному преобразованию Фурье от ${{\tilde {\Psi }}_{{jl}}}$ [5]:
(48)
${{\Psi }_{{jl}}} = \frac{1}{{{{N}_{\varphi }}{{N}_{\theta }}}}\sum\limits_{j'l'} {{{{\tilde {\Psi }}}_{{j'l'}}}\exp \left( {i\frac{{2\pi jj{\kern 1pt} '}}{{{{N}_{\varphi }}}} + i\frac{{2\pi ll{\kern 1pt} '}}{{{{N}_{\theta }}}}} \right)} .$Для учета того, что один и тот же шаг дискретизации по угловым координатам при разных $r$ соответствует разным пространственным масштабам, мы используем адаптивную дискретизацию. На каждом фазовом экране выполняется оценка необходимого шага дискретизации в угловых координатах, и если текущий шаг дискретизации превышает эту оценку, то выполняется удвоение разрешения. Для этой цели используется интерполяция Котельникова: в пространстве Фурье-образов сетка частот дополняется так, чтобы при том же частотном разрешении максимальная частота стала вдвое выше. В добавленных узлах сетки Фурье-образ поля задается равным 0. После обратного преобразования Фурье мы получаем поле, интерполированное на пространственную сетку с вдвое меньшим шагом дискретизации.
Рассмотрим вопрос численной эффективности метода. Как для плоских, так и для сферических экранов шаг дискретизации должен быть не более характерного масштаба среды (порядка или больше внутреннего масштаба для турбулентности). Однако для плоских фазовых экранов необходимо также учесть, что на краях имеется регулярный набег фазы порядка $\varphi = {{kr{{\alpha }^{2}}} \mathord{\left/ {\vphantom {{kr{{\alpha }^{2}}} 2}} \right. \kern-0em} 2},$ составляющий в нашем примере около 5000 радиан. Необходимый шаг дискретизации равен $r\Delta \alpha = \frac{{r\Delta \varphi }}{{{{d\varphi } \mathord{\left/ {\vphantom {{d\varphi } {d\alpha }}} \right. \kern-0em} {d\alpha }}}}$ = $\frac{{\lambda \Delta \varphi }}{{2\pi \alpha }},$ где $\Delta \varphi $ – допустимая вариации фазы между дискретными выборками поля. Если принять $\Delta \varphi = \frac{\pi }{4},$ то $r\Delta \alpha = \frac{\lambda }{{8\alpha }} \approx 0.2$ мм. При указанной в статье расходимости характерный размер луча достигает 5 м, что потребует размерности сетки порядка $N = 6 \times {{10}^{8}}$ точек, что является очень большой величиной, требующей не только большого времени, но и оперативной па-мяти, не всегда доступной на современных процессорах. Фактически же для счета достаточно шага около 3 мм, что понижает размерность сетки более, чем в 100 раз, а скорость вычисления быстрого преобразования Фурье, пропорциональная $N\lg N,$ увеличивается в еще большей мере.
Размер фазового экрана обычно близок к размеру поперечного сечения пучка с некоторым запасом для учета возможного уширения пучка. Однако при таком подходе к моделированию не учитывается влияние низкочастотной части спектра случайных неоднородностей, в частности внешнего масштаба, если он существенно превышает размер пучка.
РЕЗУЛЬТАТЫ
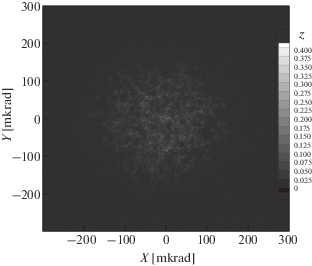
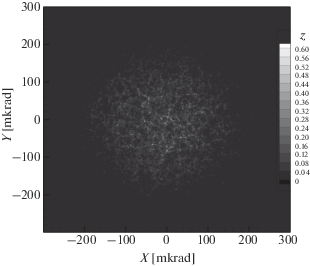
На рис. 1–6 показаны примеры численного расчета распределений амплитуды гауссова лазерного пучка с длиной волны $\lambda = 354.84$ нм с расходимостью $2\alpha = 0.3 \times {{10}^{{ - 3}}}$ рад на различных точках трассы длиной 24 км для $2.5 \times {{10}^{{ - 15}}}\,\,{{{\text{м}}}^{{ - 2/3}}}$. Рисунки демонстрируют формирование режима спеклов. Шаг между фазовыми экранами составлял 100 м.
Рис. 1.
Распределение амплитуды в сечении пучка расходимостью $2\alpha = 0.3 \times {{10}^{{ - 3}}}$ рад для $C_{n}^{2} = 2.5 \times $ $ \times \,\,{{10}^{{ - 15}}}\,\,{{{\text{м}}}^{{ - 2/3}}}$ на расстоянии 1 км от источника.
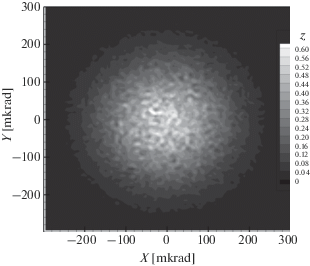
Рис. 2.
Распределение амплитуды в сечении пучка расходимостью $2\alpha = 0.3 \times {{10}^{{ - 3}}}$ рад для $C_{n}^{2} = 2.5 \times $ $ \times \,\,{{10}^{{ - 15}}}\,\,{{{\text{м}}}^{{ - 2/3}}}$ на расстоянии 2 км от источника.
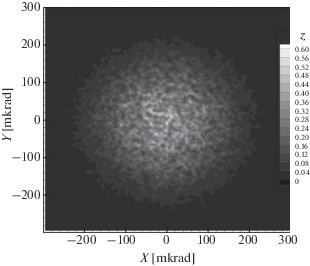
Рис. 3.
Распределение амплитуды в сечении пучка расходимостью $2\alpha = 0.3 \times {{10}^{{ - 3}}}$ рад для $C_{n}^{2} = 2.5 \times $ $ \times \,\,{{10}^{{ - 15}}}\,\,{{{\text{м}}}^{{ - 2/3}}}$ на расстоянии 4 км от источника.
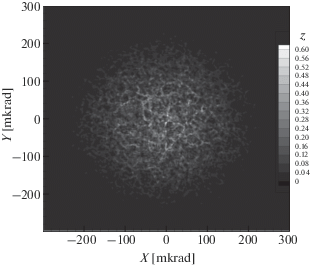
Рис. 4.
Распределение амплитуды в сечении пучка расходимостью $2\alpha = 0.3 \times {{10}^{{ - 3}}}$ рад для $C_{n}^{2} = 2.5 \times $ $ \times \,\,{{10}^{{ - 15}}}\,\,{{{\text{м}}}^{{ - 2/3}}}$ на расстоянии 8 км от источника.
ЗАКЛЮЧЕНИЕ
В данной работе мы разработали новую модификацию метода фазовых экранов, обеспечивающую уменьшение вычислительных затрат при расчете расходящихся волновых пучков. Это достигается за счет использования сферических фазовых экранов, повторяющих форму невозмущенных волновых фронтов. В малоугловом приближении мы получили выражение для вакуумного пропагатора, описывающего распространение с экрана на экран. Также нами получена формула, связывающая спектральную плотность изотропных флуктуаций индекса рефракции с фазовым набегом в сферическом слое случайной среды. Эта формула аналогична формуле для плоского слоя. Численная реализация метода сферических фазовых экранов близка к численной реализации метода плоских экранов. В работе приведены численные примеры расчета флуктуаций лазерного пучка на трассе длиной 25 км в режимах слабых и сильных флуктуаций.
Список литературы
Миронов В.Л., Тузова С.И. Метод Гюйгенса–Кирхгофа в задачах распространения оптического излучения в среде с дискретными крупномасштабными неоднородностями // Известия высших учебных заведений. Радиофизика. 1984. Т. 27. № 4. С. 535–537.
Martin J.M., Flatté S.M. Simulation of point-source scintillation through three-dimensional random media // J. Opt. Soc. Am. A. 1990. V. 7. № 5. P. 838–847.
Martin J. Simulation of wave propagation in random media: theory and aPlications // Wave Propagation in Random Media (Scintillations), edited by V.I. Tatarskii, A. Ishimaru, and V.U. Zavorotny. P. 133–141. Int. Soc. for Opt. Eng., Bellingham, Wash., Bristol: Inst. of Phys. Publishing, Pa., 1992.
Кандидов В.П. Метод Монте-Карло в нелинейной статистической оптике // Успехи физических наук. 1996. Т. 166. № 12. С. 1309–1338.
Лукин И.П., Рычков Д.С., Фалиц А.В., Лай Кин Сенг, Лю Мин Ронг. Модель фазового экрана для численного моделирования распространения лазерного пучка в дожде // Квантовая электроника. 2009. Т. 39. № 9. С. 863–868.
Gorbunov M.E., Gurvich A.S. Microlab-1 experiment: multipath effects in the lower troposphere // J. Geophysical Research – Atmospheres. 1998. V. 103. № D12. P. 13.819–13.826. https://doi.org/10.1029/98JD00806
Cao Y., Dvorak S. L., Ye X., Herman B. A new cylindrical phase screen method for modeling electromagnetic wave propagation through an inhomogeneous 2-D atmosphere // Radio Sci. 2007. V. 42. RS4027.https://doi.org/10.1029/2006rs003550
Gorbunov M.E., Vorob’ev V.V., Lauritsen K.B. Fluctuations of refractivity as a systematic error source in radio occultations // Radio Science. 2015. V. 50. № 7. P. 656–669. https://doi.org/10.1002/2014RS005639
Charnotskii M.I., Gozani J., Tatarskii V.I., Zavorotny V.U. IV Wave Propagation Theories in Random Media Based on the Path-Integral Approach // Progress in Optics, Elsevier. 1993. P. 203–266.
Зверев В.А. Радиооптика, М.: Советское радио, 1975. 304 с.
DELICAT: http://www.delicat.inoe.ro/.
Vrancken P. DELICAT – Demonstration of Lidar-Based CAT (Clear Air Turbulence) detection // Aviation Turbulence Workshop, August 2013, NCAR, Boulder, CO, USA.
Talanov V.I. Focusing of light in cubic media // ЖЭТФ. Письма в редакцию. 1970. V. 11. № 6. P. 303–305.
Розанов Н.Н. Специальные разделы математической физики. Часть I. Электромагнитные волны в вакууме. СПб: СПб ГУИТМО, 2005. 60 с.
Гурбатов С.Н., Руденко О.В., Саичев А.И. Волны и структуры в нелинейных средах без дисперсии. Приложения к нелинейной акустике. М.: Физматлит, 2008. 496 с.
Rino C.L. The Theory of Scintillation with Applications in Remote Sensing. Wiley–IEEE Press, 2011. 230 p.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Физика атмосферы и океана