Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 1, стр. 76-88

1. ВВЕДЕНИЕ

При оценке влияния турбулентности тропосферы на распространение электромагнитных волн и света во многих случаях используют модель развитой локально однородной изотропной турбулентности Колмогорова [1]. Эта модель предполагает существование инерционного интервала каскадной передачи энергии турбулентных вихрей от крупных к мелким. Этот процесс начинается с вихрей большого размера (так называемый внешний масштаб турбулентности) и заканчивается на мелких вихрях, размер которых (внутренний масштаб турбулентности) определяется диссипацией кинетической энергии в ламинарных течениях. При этом не учитывается наличие силы тяжести, которая приводит к возникновению в тропосфере внутренних гравитационных волн [2].

Взаимодействие внутренних гравитационных волн с конвективными турбулентными потоками часто (при положительных значениях числа Ричардсона) приводит к устойчивой вертикальной стратификации слоев (см., например, [3]). Характерные вертикальные масштабы слоев лежат в интервале от сотен до единиц метров, а горизонтальные – в 10–100 раз больше. Следуя [4], мы будем называть такие неоднородности анизомерными, оставив термин “анизотропный” за средами, диэлектрическая проницаемость которых описывается тензором, а за интервалом их масштабов сохраним название инерционный интервал.

В предположении о статистической однородности флуктуаций диэлектрической проницаемости $\delta \varepsilon ({\mathbf{r}}) = \varepsilon ({\mathbf{r}}) - \left\langle {\varepsilon ({\mathbf{r}})} \right\rangle $ мерой “удельных весов” неоднородностей разных масштабов и ориентаций является трехмерный пространственный спектр ${{\Phi }_{\varepsilon }}(\kappa )$, который связан с корреляционной функцией диэлектрической проницаемости соотношением [1]

В случае локальной однородности флуктуаций диэлектрической проницаемости корреляционная функция может не существовать из-за расходимости интеграла (1.1) при $\kappa = 0$¹¹. В этом случае вводится структурная функция

которая в случае однородных флуктуаций выражается через корреляционную функцию:

Модели трехмерных спектров температуры и плотности газа в устойчиво-стратифицированной атмосфере для волновых чисел, отвечающих инерционному интервалу, рассмотрены, например, в работах [3, 5–8], где проведено сравнение с экспериментальными данными, в которых, как правило, оцениваются одномерные спектры (в направлении некоторого единичного вектора ${\mathbf{e}}$, обычно в вертикальном ${{{\mathbf{e}}}_{z}}$ и горизонтальном ${{{\mathbf{e}}}_{{xy}}} \bot {{{\mathbf{e}}}_{z}}$ направлениях):

где интегрирование проводится по перпендикулярным к ${\mathbf{e}}$ компонентам вектора $\kappa = {{\kappa }_{{\mathbf{e}}}}{\mathbf{e}} + {{\kappa }_{ \bot }}$.

Механизмы формирования одномерных (вертикальных и горизонтальных) спектров в инерционном интервале предложены в ряде работ [9, 10]. В инерционном интервале одномерный спектр анизомерной турбулентности в устойчиво стратифицированной среде как функция волнового числа изменяется по степенному закону с показателем степени –3:

отличающемуся от колмогоровской зависимости ${{V}_{\varepsilon }}(\kappa {\mathbf{e}}) \sim {{\kappa }^{{ - 5/3}}}.$ Экстраполяция соответствующего (1.5) трехмерного спектра ${{\Phi }_{\varepsilon }}(\kappa ) \sim {{\kappa }^{{ - 5}}}$ на область малых волновых чисел приводит к расходимости не только корреляционной функции (1.1), но и структурной функции (1.2). Поэтому возникает необходимость дополнения этих моделей в области малых волновых чисел.

В данной работе предлагается модель трехмерного спектра диэлектрической проницаемости в устойчиво-стратифицированной атмосфере, которая описывает основные свойства анизомерных флуктуаций и в то же время достаточно проста и пригодна для аналитических расчетов корреляционной функции флуктуаций диэлектрической проницаемости и фазы распространяющейся в такой среде электромагнитной волны.

2. МОДЕЛЬ ПОДОБИЯ АНИЗОМЕРНЫХ ФЛУКТУАЦИЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ В ТУРБУЛЕНТНОЙ АТМОСФЕРЕ (ТРОПОСФЕРЕ)

В устойчиво-стратифицированной атмосфере одномерные спектры в вертикальном, горизонтальном, а также в других направлениях подобны друг другу, различаясь лишь масштабами корреляции. Пусть $L_{0}^{{x,y,z}}$ – характерные линейные размеры неоднородностей (масштабы корреляции) вдоль осей координат x, y, z. Из экспериментальных данных следует, что анизомерные неоднородности сильно сплюснуты (их вертикальный масштаб $L_{0}^{z}$ в 10–100 раз меньше горизонтальных $L_{0}^{x} = {{\alpha }_{x}}L_{0}^{z},$ $L_{0}^{y} = {{\alpha }_{y}}L_{0}^{z}$), что отвечает значениям коэффициента вертикального сжатия

В реальности наблюдается рост масштабов турбулентности с высотой, так что обычно в тропосфере 1 м < $L_{0}^{z}$ < 150 м, тогда как в стратосфере на высотах 30–50 км: 1–100 м < $L_{0}^{z}$ < 1–10 км. Оценки масштабов турбулентности на основе экспериментальных данных приведены, например, в работах А.С. Гурвича и И.П. Чунчузова [3, 7].

Определим линейное инвариантное (по элементу объема с равным единицей якобианом) преобразование пространственных координат векторов ${\mathbf{r}} \equiv (x,y,z)$ в “сопряженную” нашей “анизомерной” “изотропную” систему координат ${\mathbf{\tilde {r}}} \equiv (\tilde {x},\tilde {y},\tilde {z})$, в которой статистические свойства флуктуаций диэлектрической проницаемости $\tilde {\varepsilon }({\mathbf{\tilde {r}}}) = \varepsilon ({\mathbf{r}})$ полагаются изотропными, так что корреляционная функция диэлектрической проницаемости

зависит только от модуля $\Delta \tilde {r} = \left| {\Delta {\mathbf{\tilde {r}}}} \right|.$ Такое преобразование векторов можно описать матрицей ${\mathbf{r}} = {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} \tilde {r}}},$ инвариантность обеспечивается условием $\det {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }} = 1$. Поскольку очевидно, что базис исходного пространства $({{{\mathbf{e}}}_{x}},{{{\mathbf{e}}}_{y}},{{{\mathbf{e}}}_{z}})$ преобразуется в “сопряженный” базис $({{{\mathbf{\tilde {e}}}}_{x}},{{{\mathbf{\tilde {e}}}}_{y}},{{{\mathbf{\tilde {e}}}}_{z}})$ обратным преобразованием ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}}^{{ - 1}}}$, то пространственные векторы ${\mathbf{r}}$ являются контравариантными векторами.

Ортогональным преобразованием векторов матрицу ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}$ всегда можно привести к диагональному виду, тогда линейное преобразование сведется к “сжатию-растяжению” координат вектора по осям координат:

где коэффициенты анизомерии ${{\beta }_{{x,y,z}}} > 0,$ а инвариантность элемента объема приводит к соотношению ${{\beta }_{x}}{{\beta }_{y}}{{\beta }_{z}} = 1.$ Здесь мы ограничимся “естественной” ориентацией осей координат $(x,y,z)$ в турбулентной атмосфере с диагональной матрицей преобразования ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}$.

Определив единичный вектор направления вектора $\Delta {\mathbf{r}}$ как ${\mathbf{e}} = {{\Delta {\mathbf{r}}} \mathord{\left/ {\vphantom {{\Delta {\mathbf{r}}} {\Delta r}}} \right. \kern-0em} {\Delta r}},$ из (2.3) находим безразмерный коэффициент преобразования модулей вектора:

Из выражения (2.2) с учетом (2.4) получаем

то есть анизомерия флуктуаций в модели подобия сводится к “изотропной” корреляции в “сопряженной” системе координат с безразмерным масштабирующим коэффициентом (2.4).

Введем характерные волновые числа ${{{\rm K}}_{{x,y,z}}}$ = ${{ = 2\pi } \mathord{\left/ {\vphantom {{ = 2\pi } {L_{0}^{{x,y,z}}}}} \right. \kern-0em} {L_{0}^{{x,y,z}}}}$ по осям координат, а также определим для “изотропной” системы координат ${{L}_{{{\text{iso}}}}} = \sqrt[3]{{L_{0}^{x}L_{0}^{y}L_{0}^{z}}},$ ${{{\rm K}}_{{{\text{iso}}}}} = \sqrt[3]{{{{{\rm K}}_{x}}{{{\rm K}}_{y}}{{{\rm K}}_{z}}}}$, тогда безразмерные коэффициенты анизомерии ${{\beta }_{{x,y,z}}} = {{{{{\text{K}}}_{{x,y,z}}}} \mathord{\left/ {\vphantom {{{{{\text{K}}}_{{x,y,z}}}} {{{{\text{K}}}_{{{\text{iso}}}}}}}} \right. \kern-0em} {{{{\text{K}}}_{{{\text{iso}}}}}}},$ а характерное волновое число в произвольном направлении единичного вектора ${\mathbf{e}}$ может быть представлено как

а также характерный линейный размер неоднородностей в направлении ${\mathbf{e}}$: ${{L}_{0}}({\mathbf{e}}) = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{{\rm K}}_{0}}({\mathbf{e}})}}} \right. \kern-0em} {{{{\rm K}}_{0}}({\mathbf{e}})}}.$

Аналогично (2.2) трехмерный спектр ${{\Phi }_{\varepsilon }}(\kappa )$ может быть выражен через спектр в “изотропной” системе координат. При этом волновые вектора $\kappa $ являются ковариантными векторами и преобразуются по тому же закону, что и базис (с обратной матрицей ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}}^{{ - 1}}}$):

Аналогично (2.5) трехмерный “изомерный” спектр зависит от скаляра $\tilde {\kappa } = \sqrt {{{\kappa _{x}^{2}} \mathord{\left/ {\vphantom {{\kappa _{x}^{2}} {\beta _{x}^{2}}}} \right. \kern-0em} {\beta _{x}^{2}}} + {{\kappa _{y}^{2}} \mathord{\left/ {\vphantom {{\kappa _{y}^{2}} {\beta _{y}^{2}}}} \right. \kern-0em} {\beta _{y}^{2}}} + {{\kappa _{z}^{2}} \mathord{\left/ {\vphantom {{\kappa _{z}^{2}} {\beta _{z}^{2}}}} \right. \kern-0em} {\beta _{z}^{2}}}} ,$ который для удобства можно выразить через безразмерный скаляр

так что $\tilde {\kappa }(\kappa ) = {{{\rm K}}_{{{\text{iso}}}}} \cdot \sqrt {S(\kappa )} ,$ а форма спектра описывается функцией $\Phi _{\varepsilon }^{0}(S).$

С использованием формул (2.8), (2.9) получаем подобие одномерных спектров:

здесь введена одномерная спектральная функция

Аналогично (2.9) можно выразить одномерный “анизомерный” спектр через “изотропный”:

где введен зависящий от направления ${\mathbf{e}}$ безразмерный масштабирующий коэффициент то есть аналогично (2.5) анизомерия одномерных спектров приводит к одномерному спектру в “сопряженной” системе координат $V_{\varepsilon }^{{{\text{iso}}}}(\tilde {\kappa })$ = $ = {\rm K}_{{{\text{iso}}}}^{2} \cdot {{\phi }_{\varepsilon }}({{{{{\tilde {\kappa }}}^{2}}} \mathord{\left/ {\vphantom {{{{{\tilde {\kappa }}}^{2}}} {{\rm K}_{{{\text{iso}}}}^{2}}}} \right. \kern-0em} {{\rm K}_{{{\text{iso}}}}^{2}}})$ с безразмерным масштабирующим коэффициентом (2.13).

Выражение (2.12) явно демонстрирует подобие формы одномерных спектров в разных направлениях: они имеют одинаковую зависимость от волнового числа ${{\kappa }_{{\mathbf{e}}}}$ и различаются лишь значениями масштабирующего коэффициента $\gamma ({\mathbf{e}})$. Например, для спектров $V_{\varepsilon }^{x},\,\,V_{\varepsilon }^{y},\,\,V_{\varepsilon }^{z}$ вдоль декартовых осей имеем ${{\gamma }_{{x,y,z}}} \equiv \gamma ({{{\mathbf{e}}}_{{x,y,z}}})$ = ${{{{{\rm K}}_{{{\text{iso}}}}}} \mathord{\left/ {\vphantom {{{{{\rm K}}_{{{\text{iso}}}}}} {{{{\rm K}}_{{x,y,z}}}}}} \right. \kern-0em} {{{{\rm K}}_{{x,y,z}}}}} = {{L_{0}^{{x,y,z}}} \mathord{\left/ {\vphantom {{L_{0}^{{x,y,z}}} {{{L}_{{{\text{iso}}}}}}}} \right. \kern-0em} {{{L}_{{{\text{iso}}}}}}}$ и из определений (1.1) и (1.2) корреляционной и структурной функций находим:

где $\Delta {{r}_{{{\text{eff}}}}}(\Delta {\mathbf{r}}) = {{\Delta r} \mathord{\left/ {\vphantom {{\Delta r} {\gamma ({\mathbf{e}})}}} \right. \kern-0em} {\gamma ({\mathbf{e}})}} = \Delta r \cdot [{{{{{\rm K}}_{0}}({\mathbf{e}})} \mathord{\left/ {\vphantom {{{{{\rm K}}_{0}}({\mathbf{e}})} {{{{\rm K}}_{{{\text{iso}}}}}}}} \right. \kern-0em} {{{{\rm K}}_{{{\text{iso}}}}}}}]$ – эффективная разность координат в направлении ${\mathbf{e}}$.

В частности, для горизонтально однородной атмосферы $L_{0}^{x} = L_{0}^{y},$ ${{{\rm K}}_{x}} = {{{\rm K}}_{y}},$ а $\alpha \equiv {{L_{0}^{{x,y}}} \mathord{\left/ {\vphantom {{L_{0}^{{x,y}}} {L_{0}^{z}}}} \right. \kern-0em} {L_{0}^{z}}}$ (см. (2.1)), множитель $\gamma ({\mathbf{e}})$ зависит от угла $\theta $ между вектором ${\mathbf{e}}$ и осью $z$ $\left( {\cos \theta = {{e}_{z}}} \right).$ В этом случае находим

Здесь мы учли определение ${{{\rm K}}_{{{\text{iso}}}}} = \sqrt[3]{{{{{\rm K}}_{x}}{{{\rm K}}_{y}}{{{\rm K}}_{z}}}}.$

На рис. 1 приведены графики зависимости масштабирующего коэффициента $\gamma ({\mathbf{e}})$ в зависимости от угла скольжения $\psi = \left| {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} - \theta } \right| = \left| {\arcsin {{e}_{z}}} \right|$ при разных коэффициентах вертикального сжатия $\alpha $ (случай горизонтально однородной атмосферы).

Аналогично (2.10) для модели подобия (2.3), (2.4) выразим функцию корреляции (2.5) через одномерную спектральную функцию (2.11):

3. СТЕПЕННАЯ АНИЗОМЕРНАЯ МОДЕЛЬ ФЛУКТУАЦИЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ

Здесь мы предлагаем степенную анизомерную модель флуктуаций диэлектрической проницаемости, близкую к степенной в инерционном интервале спектра пространственных частот (при $S(\kappa ) \gg 1$ полагаем $\Phi _{\varepsilon }^{0}(S(\kappa )) \sim S{{(\kappa )}^{{ - p}}}$) и корректирующую степенную при больших пространственных масштабах турбулентности (при ${{\kappa }_{{\mathbf{e}}}} \leqslant {{{\rm K}}_{0}}({\mathbf{e}})$ полагаем $\Phi _{\varepsilon }^{0}(S(\kappa )) \sim S{{(\kappa )}^{n}}$):

где $\sigma _{\varepsilon }^{2} = {{B}_{\varepsilon }}(0)$ – дисперсия флуктуаций диэлектрической проницаемости, $\Gamma (z)$ – гамма-функция. Использованная в [8] модель трехмерного спектра показателя преломления среды, флуктуации в которой изотропны в горизонтальной плоскости, с точностью до обозначений и экспоненциального множителя, обрезающего спектр в области малых масштабов (при $S(\kappa ) \gg 1$), совпадает с (3.1) при n = 0 и Κ_x = Κ_y . Введение множителя ${{{{S}^{n}}(\kappa )} \mathord{\left/ {\vphantom {{{{S}^{n}}(\kappa )} {{{{(1 + S(\kappa ))}}^{n}}}}} \right. \kern-0em} {{{{(1 + S(\kappa ))}}^{n}}}},$ “вырезающего” наиболее крупные неоднородности при $S(\kappa ) \ll 1,$ придает модели дополнительную гибкость при описании спектра в области больших масштабов²².

Нетрудно найти, что $p = {{11} \mathord{\left/ {\vphantom {{11} 6}} \right. \kern-0em} 6}$ соответствует колмогоровской локально однородной изотропной турбулентности $({{\Phi }_{\varepsilon }}(\kappa ) \sim {{\left| \kappa \right|}^{{ - 11/3}}})$, тогда как $p = {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}$ соответствует анизомерной устойчиво стратифицированной среде с зависимостью (1.5). Для краткости назовем спектр среды с устойчивой (развитой) стратификацией “приземным”.

Поскольку анизомерность в модели подо-бия (2.14) определяется масштабирующим множителем $\gamma ({\mathbf{e}})$, то характер корреляции флуктуаций диэлектрической проницаемости описывается поведением сопряженной изотропной модели с ${{S}_{{{\text{iso}}}}}(\kappa ) = {{{{\kappa }^{2}}} \mathord{\left/ {\vphantom {{{{\kappa }^{2}}} {{\rm K}_{{{\text{iso}}}}^{2}}}} \right. \kern-0em} {{\rm K}_{{{\text{iso}}}}^{2}}}.$ Для “изотропного” коэффициента корреляции из (2.16) имеем

Подставляя сюда степенную модель флуктуаций (3.1), находим выражение

где $\delta = {{{\rm K}}_{{{\text{iso}}}}}\Delta r$ – безразмерная разность координат.

В Приложении 1 приведен явный вид “нормированного” коэффициента корреляции $R_{\varepsilon }^{0}(p,n,\delta )$ для “колмогоровского” $(p = {{11} \mathord{\left/ {\vphantom {{11} 6}} \right. \kern-0em} 6})$ и “приземного” спектров $(p = {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2})$ для частных случаев $n = 0;1.$

На рис. 2 приведены графики зависимости функции $R_{\varepsilon }^{0}(p,n,\delta )$ от безразмерной разности координат $\delta $ при частных значениях параметров $p,n.$

В табл. 1 приведены асимптотики коэффициента $R_{\varepsilon }^{0}(p,n,x)$ при разных режимах турбулентности.

Приведем выражения для одномерного спектра флуктуаций диэлектрической проницаемости (2.10) для степенной модели подобия (3.1) в сопряженной “изотропной” системе координат. Путем несложных вычислений находим:

где введены

В Приложении 1 приведены формулы для коэффициента (3.6) и интеграла (3.8) для “колмогоровского” $(p = {{11} \mathord{\left/ {\vphantom {{11} 6}} \right. \kern-0em} 6})$ и “приземного” спектров $(p = {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2})$ для целочисленных $n$.

В инерционном интервале $\kappa \gg {{{\rm K}}_{{{\text{iso}}}}} \Rightarrow k \gg 1$ полагаем $\lambda (k) \approx {{k}^{{ - 2}}} \ll 1,$ ${{I}_{0}}(p,n,\lambda (k)) \approx {1 \mathord{\left/ {\vphantom {1 {(p - 1)}}} \right. \kern-0em} {(p - 1)}},$ и выражение (3.5) упрощается:

Приведем на основе формул (2.12) и (3.5) оценку дисперсии флуктуаций диэлектрической проницаемости. Действительно, согласно степенной модели относительных температурных флуктуаций в сильно стратифицированной тропосфере, описанной в работе [3], вертикальный спектр относительных температурных флуктуаций имеет вид:

где коэффициент ${{A}_{0}} \approx 0.1,$ $N$ – частота плавучести, $g$ – ускорение свободного падения. Для внешнего вертикального масштаба турбулентности имеем оценку: где ${{\sigma }_{w}}$ – среднеквадратичные пульсации скорости ветра.

С другой стороны, оценка вертикального спектра на основе формул (2.12) и (3.5) при выбранных параметрах $p = {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2},$ $n = 0$ в инерционном интервале ${{\kappa }_{z}} \gg {{\kappa }_{0}}$ дает выражение

Учтем далее, что флуктуации диэлектрической проницаемости связаны с температурными флуктуациями соотношением [1]

где p – давление воздуха в миллибарах, а T – абсолютная температура в градусах Кельвина. Из сравнения формул (3.10) и (3.12) с учетом (3.11) и (3.13) находим

Подставляя сюда характерные для спокойной приземной атмосферы параметры ${{A}_{0}} \approx 0.1,$ $N \approx 0.02\,\,{{{\text{c}}}^{{ - 1}}},$ σ_w ≈ 0.5 м/с, g ≈ 10 м/с², $p \approx 1000\,\,{\text{мб,}}$ $T \approx 280\,\,{\text{K,}}$ получаем числовую оценку дисперсии флуктуаций диэлектрической проницаемости:

Полученная оценка удовлетворительно согласуется с оценками, приведенными в [1]. В условиях сильной возмущенности атмосферы значение $\sigma _{\varepsilon }^{2}$ может увеличиться на порядок или даже больше.

4 КОРРЕЛЯЦИЯ ФЛУКТУАЦИЙ ФАЗЫ И ЭЙКОНАЛА ВОЛНЫ В ТУРБУЛЕНТНОЙ АНИЗОМЕРНОЙ СРЕДЕ

Рассмотрим далее корреляционные свойства фазы и эйконала волны, распространяющихся в среде с анизомерными неоднородностями. Пусть по направлению единичного вектора ${{{\mathbf{e}}}_{s}}$ от начала координат распространяется плоская волна с частотой $\omega $ (и волновым вектором ${\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}$) Используем далее введенную нами модель подобия анизомерных флуктуации диэлектрической проницаемости.

При переходе в “изотропную” систему координат единичный вектор направления распространения плоской волны ${{{\mathbf{e}}}_{s}} \equiv ({{e}_{{sx}}},{{e}_{{sy}}},{{e}_{{sx}}})$ преобразуется в вектор

и уже не обязательно является единичным: $\left| {{{{\mathbf{E}}}_{s}}} \right| = {{\beta }_{0}}({{{\mathbf{e}}}_{s}}).$ Единичным, очевидно, является вектор ${{{\mathbf{\tilde {e}}}}_{s}} \equiv ({{\tilde {e}}_{{sx}}},{{\tilde {e}}_{{sy}}},{{\tilde {e}}_{{sx}}}) = {{{{{\mathbf{E}}}_{s}}} \mathord{\left/ {\vphantom {{{{{\mathbf{E}}}_{s}}} {{{\beta }_{0}}({{{\mathbf{e}}}_{s}})}}} \right. \kern-0em} {{{\beta }_{0}}({{{\mathbf{e}}}_{s}})}}.$

В геометрооптическом (коротковолновом) приближении фаза волны пропорциональна эйконалу (${\text{Ph}}({\mathbf{r}}) = ({\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c})\Theta ({\mathbf{r}})$), а в первом приближении по малой поправке $\nu ({\mathbf{r}})$ к диэлектрической проницаемости $\varepsilon ({\mathbf{r}}) = 1 + \nu ({\mathbf{r}})$ имеем уравнение эйконала $2({{{\mathbf{e}}}_{s}}\nabla )\Theta ({\mathbf{r}}) = \nu ({\mathbf{r}}).$ Существенно, что при преобразовании координат к сопряженной “изотропной” системе уравнение эйконала $\Theta ({\mathbf{r}})$ принимает вид

где оператор $\tilde {\nabla }$ действует по “изотропной” координате ${\mathbf{\tilde {r}}}$. Из уравнения (4.2) сразу следует, что все статистические характеристики эйконала волны, распространяющейся в анизомерной среде, описываются эквивалентным изотропным спектром, а анизомерия определяется законом перехода к “изотропным” координатам и множителем $\beta _{0}^{{ - 1}}({{{\mathbf{e}}}_{s}}).$

Представим структурную функцию эйконала на расстоянии $s$ от источника в виде

где $\sigma _{\Theta }^{2}({{{\mathbf{e}}}_{s}},s) = {{B}_{\Theta }}({{{\mathbf{e}}}_{s}},s,{\mathbf{0}})$ – дисперсия, а ${{R}_{\Theta }}({{{\mathbf{e}}}_{s}},s,\Delta {\mathbf{r}})\, = $ = ${{{{B}_{\Theta }}({{{\mathbf{e}}}_{s}},s,\Delta {\mathbf{r}})} \mathord{\left/ {\vphantom {{{{B}_{\Theta }}({{{\mathbf{e}}}_{s}},s,\Delta {\mathbf{r}})} {\sigma _{\Theta }^{2}({{{\mathbf{e}}}_{s}},s)}}} \right. \kern-0em} {\sigma _{\Theta }^{2}({{{\mathbf{e}}}_{s}},s)}}$ – коэффициент корреляции эйконала.

Следуя выкладкам [1], нетрудно получить выражение для дисперсии в малоугловом приближении:

где ${{\phi }_{\varepsilon }}(0) = 2\pi \int_0^\infty {kdk\Phi _{\varepsilon }^{0}({{k}^{2}})} $ – значение в нуле одномерной спектральной функции (2.11), а интегрирование по ${{\kappa }_{\rho }}$ ведется в плоскости волновых векторов ${{\mathbb{S}}_{s}}$: ${{\kappa }_{\rho }} \in {{\mathbb{S}}_{s}} \equiv {{\kappa }_{\rho }} \bot {{{\mathbf{e}}}_{s}}.$

В соответствии с моделью подобия анизомерных флуктуаций коэффициент корреляции эйконала связан с “изотропным” коэффициентом корреляции соотношением

Здесь мы учли (см. [1]), что в малоугловом приближении в изотропной атмосфере масштаб корреляции в направлении распространения ${{{\mathbf{\tilde {e}}}}_{s}}$ велик и корреляция зависит от поперечной к ${{{\mathbf{\tilde {e}}}}_{s}}$ разности координат $\Delta {{\tilde {r}}_{ \bot }}$. Аналогично выводу (4.4) находим для коэффициента корреляции:

где $\rho = \Delta {{\tilde {r}}_{ \bot }}({{{\mathbf{e}}}_{s}},\Delta {\mathbf{r}}),$ ${{J}_{0}}$ – функция Бесселя.

Таким образом, изомерию флуктуаций можно учесть, оценив поперечную разность $\Delta {{\tilde {r}}_{ \bot }}$ в “изотропной” системе координат в зависимости от направления волны ${{{\mathbf{e}}}_{s}}$ и разности $\Delta {\mathbf{r}}$.

Для этого аналогично (4.1) определим единичный вектор поперечной компоненты вектора $\Delta {\mathbf{r}}$, лежащий в плоскости ${{\mathbb{S}}_{s}} \bot {{{\mathbf{e}}}_{s}}$: ${{{\mathbf{e}}}_{ \bot }} = {{\Delta {{{\mathbf{r}}}_{ \bot }}} \mathord{\left/ {\vphantom {{\Delta {{{\mathbf{r}}}_{ \bot }}} {\Delta {{r}_{ \bot }}}}} \right. \kern-0em} {\Delta {{r}_{ \bot }}}}.$ В “изотропной” системе координат он имеет компоненты

Заметим, что ${{{\mathbf{E}}}_{ \bot }}$ зависит от ${{{\mathbf{e}}}_{s}}$ опосредованно, так как ${{{\mathbf{e}}}_{ \bot }} \bot {{{\mathbf{e}}}_{s}}$ и не обязательно единичный.

Поскольку параллельная к направлению волны ${{{\mathbf{e}}}_{s}}$ компонента $\Delta {{{\mathbf{r}}}_{\parallel }} = \Delta {\mathbf{r}} - \Delta {{{\mathbf{r}}}_{ \bot }} = \Delta {{r}_{\parallel }}{{{\mathbf{e}}}_{s}}$ при переходе к “изотропным” координатам переходит в параллельную к направлению ${{{\mathbf{\tilde {e}}}}_{s}}$ компоненту $\Delta {{{\mathbf{\tilde {r}}}}_{\parallel }} = \Delta {{r}_{\parallel }}{{{\mathbf{E}}}_{s}}$ = $\Delta {{r}_{\parallel }}{{\beta }_{0}}({{{\mathbf{e}}}_{s}}) \cdot {{{\mathbf{\tilde {e}}}}_{s}},$ то компонента $\Delta {{{\mathbf{r}}}_{\parallel }}$ не будет влиять на поперечную разность $\Delta {{\tilde {r}}_{ \bot }}$, входящую в (4.5). То есть имеем $\Delta {{\tilde {r}}_{ \bot }}({{{\mathbf{e}}}_{s}},\Delta {\mathbf{r}})$ = $\Delta {{\tilde {r}}_{ \bot }}({{{\mathbf{e}}}_{s}},\Delta {{{\mathbf{r}}}_{ \bot }}).$ Поэтому представляем поперечный вектор в “изотропной” системе координат в виде

Из выражения (4.8) легко получить связь между модулями поперечных (к направлению падающей волны) компонент вектора $\Delta {\mathbf{r}}$ в исходной и “изотропной” системах координат:

Определим также коэффициент “масштабируемости” пространственной корреляции

Здесь $\varepsilon $ – угол между векторами ${{{\mathbf{E}}}_{ \bot }}({{{\mathbf{e}}}_{s}},{{{\mathbf{e}}}_{ \bot }})$ и ${{{\mathbf{E}}}_{s}}({{{\mathbf{e}}}_{s}})$.

Тогда для эффективного поперечного аргумента коэффициента корреляции $\Delta {{r}_{{ \bot {\text{eff}}}}} = \Delta {{\tilde {r}}_{ \bot }}({{{\mathbf{e}}}_{s}},\Delta {\mathbf{r}})$ имеем

Отметим, что выражения(4.5), (4.8), (4.9) получены в модели подобия анизомерных флуктуаций без использования конкретных выражений для скаляра $S(\kappa )$.

Если ввести углы $({{\theta }_{s}},{{\varphi }_{s}})$ для вектора ${{{\mathbf{e}}}_{s}}$ в сферической системе координат, а также полярный угол ${{\psi }_{\rho }}$ вектора ${{{\mathbf{e}}}_{ \bot }}$ в полярной системе координат на плоскости ${{\mathbb{S}}_{s}} \bot {{{\mathbf{e}}}_{s}}$ (при ${{\psi }_{\rho }} = 0\,\, \to \,\,{{{\mathbf{e}}}_{ \bot }} \bot {{{\mathbf{e}}}_{z}}$), то коэффициент масштабируемости (4.10) будет зависеть от данных углов.

В Приложении 2 получены явные выражения для коэффициента масштабируемости $C({{{\mathbf{e}}}_{s}},{{{\mathbf{e}}}_{ \bot }})$ = $ = C({{\theta }_{s}},{{\varphi }_{s}},{{\psi }_{\rho }}),$ а также его максимального и минимального значений для выбранного направления ${{{\mathbf{e}}}_{s}} = ({{\theta }_{s}},{{\varphi }_{s}})$.

Приведем два примера.

1. Для горизонтально изотропной атмосферы ${{\beta }_{x}} = {{\beta }_{y}} = {{\beta }_{{xy}}},$ ${{\beta }_{z}} = \beta _{{xy}}^{{ - 2}},$ ${{\beta }_{{xy}}} < 1 < {{\beta }_{z}}$ находим: ${{C}_{{\max }}}({{{\mathbf{e}}}_{s}})$ = ${{\beta }_{{xy}}}{{({{\cos }^{2}}{{\theta }_{s}} + \beta _{{xy}}^{6}{{\sin }^{2}}{{\theta }_{s}})}^{{ - 1/2}}}$ = ${{\beta }_{z}}\gamma ({{{\mathbf{e}}}_{s}})$ = $ = {{{{\beta }_{z}}} \mathord{\left/ {\vphantom {{{{\beta }_{z}}} {{{\beta }_{0}}({{{\mathbf{e}}}_{s}})}}} \right. \kern-0em} {{{\beta }_{0}}({{{\mathbf{e}}}_{s}})}}$, ${{C}_{{\min }}}({{{\mathbf{e}}}_{s}}) = {{\beta }_{{xy}}}$ и ${{{{C}_{{\max }}}({{{\mathbf{e}}}_{s}})} \mathord{\left/ {\vphantom {{{{C}_{{\max }}}({{{\mathbf{e}}}_{s}})} {{{C}_{{\min }}}({{{\mathbf{e}}}_{s}})}}} \right. \kern-0em} {{{C}_{{\min }}}({{{\mathbf{e}}}_{s}})}}$ = $\alpha \cdot \gamma ({{{\mathbf{e}}}_{s}}),$ где $\alpha = {{{{\beta }_{z}}} \mathord{\left/ {\vphantom {{{{\beta }_{z}}} {{{\beta }_{{xy}}}}}} \right. \kern-0em} {{{\beta }_{{xy}}}}}$ – коэффициент вертикального сжатия. График зависимости максимального коэффициента масштабируемости ${{C}_{{\max }}}({{{\mathbf{e}}}_{s}})$ = $ = {\alpha \mathord{\left/ {\vphantom {\alpha {\sqrt {{{{\sin }}^{2}}{{\theta }_{s}} + {{\alpha }^{2}}{{{\cos }}^{2}}{{\theta }_{s}}} }}} \right. \kern-0em} {\sqrt {{{{\sin }}^{2}}{{\theta }_{s}} + {{\alpha }^{2}}{{{\cos }}^{2}}{{\theta }_{s}}} }}$ от угла скольжения ${{\gamma }_{s}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} - {{\theta }_{s}}$ при разных значениях коэффициента вертикального сжатия приведен на рис. 3. Графики на рис. 3 аналогичны графикам рис. 1, отличие только в множителе, зависящем от коэффициента вертикального сжатия α.

2. При выбранных параметрах анизометрии $\beta _{x}^{2} = 0.05,$ $\beta _{y}^{2} = 0.2,$ $\beta _{z}^{2} = 100$ на рис. 4 приведены графики зависимости отношения ${{{{C}_{{\max }}}} \mathord{\left/ {\vphantom {{{{C}_{{\max }}}} {{{C}_{{\min }}}}}} \right. \kern-0em} {{{C}_{{\min }}}}}$ от углов $({{\gamma }_{s}},{{\varphi }_{s}})$. При этом при ${{\varphi }_{s}} = 0$ вектор ${{{\mathbf{e}}}_{s}}$ лежит в плоскости $xOz$, а коэффициент вертикального сжатия $\alpha \sim {{{{\beta }_{z}}} \mathord{\left/ {\vphantom {{{{\beta }_{z}}} {\sqrt {{{\beta }_{x}}{{\beta }_{y}}} }}} \right. \kern-0em} {\sqrt {{{\beta }_{x}}{{\beta }_{y}}} }} \approx 31.6.$

5 КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ ФЛУКТУАЦИЙ ЭЙКОНАЛА ВОЛНЫ ДЛЯ СТЕПЕННОЙ МОДЕЛИ ПОДОБИЯ

Для детализации соотношений в модели подобия используем степенную анизомерную модель (3.1) флуктуаций диэлектрической проницаемости. Для этой модели нетрудно рассчитать дисперсию флуктуаций эйконала плоской волны (4.4):

Поскольку корреляционные свойства анизомерных флуктуаций эйконала с точностью до коэффициента масштабируемости (4.10) соответствуют изотропным флуктуациям (см. (4.11)), то достаточно рассмотреть характер корреляции в “изотропном” случае. Для степенной модели коэффициент корреляции эйконала зависит от параметров модели $(p,n)$: $R_{\Theta }^{{{\text{iso}}}}(\rho ) \equiv {{R}_{{{\text{iso}}}}}(p,n,{{{\text{K}}}_{{{\text{iso}}}}}\rho ).$

В Приложении 3 приведен явный вид “нормированного” коэффициента корреляции эйконала плоской волны ${{R}_{{{\text{iso}}}}}(p,n,x)$ для “колмогоровского” $(p = {{11} \mathord{\left/ {\vphantom {{11} 6}} \right. \kern-0em} 6})$ и “приземного” спектров $(p = {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2})$ для частных случаев $n = 0;1.$

Графики функции ${{R}_{{{\text{iso}}}}}(p,n,x)$ приведены на рис. 5.

В табл. 2 приведены асимптотики коэффициента ${{R}_{{{\text{iso}}}}}(p,n,x)$ при разных режимах турбулентности.

Приведенный анализ корреляционных свойств плоской волны в турбулентной атмосфере позволяет рассмотреть и корреляционные свойства сферической волны. В малоугловом приближении коэффициент корреляции эйконала сферической волны $R_{\Theta }^{{{\text{(sph)}}}}$ связан с коэффициентом корреляции эйконала плоской волны $R_{\Theta }^{{}}$ соотношением [1]

В малоугловом приближении $\xi \Delta {{{\mathbf{r}}}_{ \bot }} \in {{\mathbb{S}}_{s}} \bot {{{\mathbf{e}}}_{s}}$ и в модели подобия анизомерных флуктуаций фазы коэффициент корреляции (5.2), как и для плоской волны (4.11), сводится к соответствующему “изотропному” коэффициенту с учетом масштабирующего множителя (4.10): $R_{\Theta }^{{{\text{(sph)}}}}({{{\mathbf{e}}}_{s}},\Delta {{{\mathbf{r}}}_{ \bot }})$ = $ = R_{\Theta }^{{{\text{iso(sph)}}}}(\Delta {{r}_{ \bot }}C({{{\mathbf{e}}}_{s}},{{{\mathbf{e}}}_{ \bot }}))$. При этом

Формулы (5.2)–(5.3) приводят к уширению интервала корреляции (по сравнению со случаем плоской волны) за счет вклада в интеграл близких более малых интервалов корреляции $0 \leqslant \Delta {{r}_{ \bot }} \leqslant \rho .$

Аналогично случаю плоской волны в Приложении 3 приведен явный вид “нормированного” коэффициента корреляции эйконала сферической волны $R_{{{\text{iso}}}}^{{{\text{sph}}}}(p,n,x)$ = $\int_0^1 {{{R}_{{{\text{iso}}}}}(p,n,x\xi )d\xi } $ для “колмогоровского” $(p = {{11} \mathord{\left/ {\vphantom {{11} 6}} \right. \kern-0em} 6})$ и “приземного” спектров $(p = {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2})$ для частных случаев $n = 0;1.$

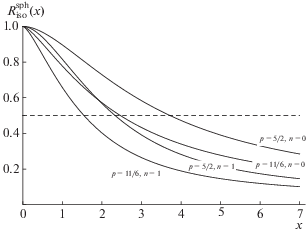
Графики функции $R_{{{\text{iso}}}}^{{{\text{sph}}}}(p,n,x)$ приведены на рис. 6.

В табл. 3 приведены асимптотики коэффициента $R_{{{\text{iso}}}}^{{{\text{sph}}}}(p,n,x)$ при разных режимах турбулентности.

Авторы благодарят рецензента за полезные конструктивные замечания.