1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 56, № 2, 2020

Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 2, стр. 245-248

Аналитическая модель плотностных течений, возникающих при оседании тяжелой примеси

Л. Х. Ингель a, b, *

a ФГБУ “НПО “Тайфун”
249038 Обнинск, ул. Победы, 4, Россия

b Институт физики атмосферы им. А.М. Обухова РАН
119017 Москва, Пыжевский пер., 3, Россия

* E-mail: lev.ingel@gmail.com

Поступила в редакцию 21.11.2018
После доработки 24.07.2019
Принята к публикации 25.09.2019

Полный текст (PDF)

Аннотация

Горизонтально-неоднородное распределение тяжелой примеси в жидкой (газообразной) среде в поле силы тяжести означает наличие горизонтальной составляющей силы градиента давления и возникновение плотностного течения. В океане течения такого типа иногда носят катастрофический характер; в атмосфере они могут иметь значение, например, в связи с некоторыми эпизодами загрязнения атмосферы, выпадением осадков, пыльными бурями, приземными метелями. В работе исследована линейная стационарная аналитическая модель, которая позволяет выявить некоторые общие закономерности плотностных течений с оседающей тяжелой примесью над горизонтальной поверхностью. Наиболее сильно амплитуда возникающих течений зависит от скорости оседания частиц и коэффициента диффузии примеси.

Ключевые слова: тяжелая примесь, оседание, плотностные течения, атмосфера, водоемы, аналитическая модель

1. ВВЕДЕНИЕ

Взвесенесущим гравитационным течениям в атмосфере и водоемах посвящена обширная литература (см., например, [1–9] и библиографию в этих изданиях). Горизонтально-неоднородное распределение тяжелой примеси в поле силы тяжести означает наличие горизонтальной составляющей силы градиента давления и возникновение плотностного течения. В океане течения такого типа иногда носят катастрофический характер [6]; в атмосфере они могут иметь значение, например, в связи с некоторыми эпизодами загрязнения атмосферы, выпадением осадков, пыльными бурями, приземными метелями. В литературе большое внимание уделяется взвесенесущим течениям над наклонными поверхностями [1–3, 5–7]. В меньшей степени изучены плотностные течения, возникающие вследствие горизонтально-неоднородного распределения тяжелой примеси над горизонтальной поверхностью. Относящиеся сюда процессы бывают включены в качестве блоков, например, в численные модели пыльных бурь, но общие закономерности таких течений, насколько нам известно, пока изучены недостаточно. В настоящей заметке исследована стационарная аналитическая модель, которая позволяет выявить некоторые общие закономерности плотностных течений с оседающей тяжелой примесью.

2. ПОСТАНОВКА ЗАДАЧИ

Рассматривается полуограниченная жидкая (газообразная) среда, ограниченная снизу твердой горизонтальной поверхностью $z = 0$ (ось $z$ направлена вертикально вверх). С этой поверхности в среду поступает тяжелая примесь:

(1)
$\chi \frac{{\partial \mu }}{{\partial z}} = - M(x)\,\,\,\,{\text{при}}\,\,\,\,z = 0.$
Здесь $\mu $ – массовая концентрация тяжелой примеси, $\chi $ – коэффициент ее диффузии, $M(x)$ – плотность потока примеси (кг/(м2 с)), которая в данной модели предполагается известной функцией горизонтальной координаты $x$ (ограничиваемся здесь двумерной задачей).

Горизонтально-неоднородное поступление примеси приводит к появлению неоднородностей плотности среды, отклонений давления и возникновению течений. Ситуация в ряде отношений аналогична задачам о термических циркуляциях – течениях, возникающих над термически-неоднородной нижней границей (см., например, [10] и библиографию в этой работе). Отличие заключается в том, что в данном случае отклонения плотности обусловлены вариациями концентрации оседающих частиц примеси. Но возникающие вертикальные движения стратифицированной по температуре среды приводят и к температурным возмущениям, вклад которых в отклонения плотности среды в общем случае также следует учитывать. Соответствующее обобщение линеаризованной системы уравнений для стационарных двумерных возмущений в приближении Буссинеска имеет вид:

(2)
$0 = - \frac{1}{{\bar {\rho }}}\frac{{\partial p}}{{\partial x}} + \nu {{\Delta }_{2}}u,\,\,\,\,0 = - \frac{1}{{\bar {\rho }}}\frac{{\partial p}}{{\partial z}} + \nu {{\Delta }_{2}}w - g\frac{{{\rho }{\kern 1pt} '}}{{\bar {\rho }}},$
(3)
$\begin{gathered} \frac{{\partial u}}{{\partial x}} + \frac{{\partial w}}{{\partial z}} = 0,\,\,\,\,\gamma w = \kappa {{\Delta }_{2}}\theta , \\ \rho {\kern 1pt} ' = \bar {\rho }\left( { - \alpha \theta + \beta \mu } \right), \\ \end{gathered} $
(4)
$ - \upsilon \frac{{d\mu }}{{dz}} = \chi {{\Delta }_{2}}\mu .$

Здесь $u,$ $w$ – составляющие возмущения поля скорости вдоль осей $x,$ $z$ соответственно; $p,$ $\rho {\kern 1pt} ',$ $\theta $ – возмущения давления, плотности и температуры (для атмосферного воздуха – потенциальной температуры [11]); $\nu ,$ $\kappa $ – коэффициенты обмена (предполагаются постоянными); $\gamma \geqslant 0$ – фоновый вертикальный градиент температуры (потенциальной температуры; предполагается устойчивая или нейтральная фоновая стратификация плотности); $\alpha $ – коэффициент теплового расширения, $\beta $ – концентрационный коэффициент плотности; $\bar {\rho }$ – средняя (отсчетная) плотность среды; ${{\Delta }_{2}}$ – символ двумерного лапласиана; $\upsilon $ – абсолютная величина скорости оседания частиц примеси (предполагается одинаковой и много большей, чем вертикальная скорость возникающих течений).

На нижней границе (подстилающей поверхности) предполагается выполнение условий непротекания и прилипания, а также фиксированной температуры (отсутствия температурных возмущений):

(5)
$u = w = 0,\,\,\,\theta = 0\,\,{\text{при}}\,\,z = 0.$

Вдали от поверхности предполагается затухание возмущений.

3. АНАЛИЗ ПОЛЯ РАСПРЕДЕЛЕНИЯ ПРИМЕСИ

Решение уравнения (4) для горизонтально-однородной задачи (когда $M$ не зависит от $x$), с учетом краевых условий, имеет вид

(6)
$\mu = \frac{M}{\upsilon }\exp \left[ {{{ - z} \mathord{\left/ {\vphantom {{ - z} {\left( {{{\chi } \mathord{\left/ {\vphantom {{\chi } \upsilon }} \right. \kern-0em} \upsilon }} \right)}}} \right. \kern-0em} {\left( {{{\chi } \mathord{\left/ {\vphantom {{\chi } \upsilon }} \right. \kern-0em} \upsilon }} \right)}}} \right].$

При достаточно слабой зависимости $M$ от $x,$ это решение, очевидно, приближенно выполняется. Из масштабного анализа легко видеть, что соответствующий критерий – малость вертикального масштаба ${{h}_{\upsilon }} \equiv {\chi \mathord{\left/ {\vphantom {\chi \upsilon }} \right. \kern-0em} \upsilon }$ по сравнению с горизонтальным масштабом ${{k}^{{ - 1}}},$ на котором заметно меняется $M.$ Ниже будет рассматриваться весьма удобная для анализа модель с гармонической горизонтальной зависимостью поступления примеси:

(7)
$M = {{M}_{0}} + {{M}_{1}}\cos \left( {kx} \right),$
где ${{M}_{0}},$ ${{M}_{1}}$ – постоянные. Решение уравнения (4) в этом случае имеет вид
(8)
$\mu = \frac{{{{M}_{0}}}}{\upsilon }\exp \left[ { - \frac{z}{{{{h}_{\upsilon }}}}} \right] + h\frac{{{{M}_{1}}}}{\chi }\exp \left[ { - \frac{z}{h}} \right]\cos \left( {kx} \right),$
где

(9)
$h = {{\left\{ {\frac{\upsilon }{{2\chi }} + {{{\left[ {{{{\left( {\frac{\upsilon }{{2\chi }}} \right)}}^{2}} + {{k}^{2}}} \right]}}^{{{\text{1/2}}}}}} \right\}}^{{ - 1}}}.$

Для рассматриваемого механизма генерации возмущений существенна горизонтальная неоднородность концентрации примеси, т.е. имеет значение только второе слагаемое в (8). Ниже предполагаются достаточно большие горизонтальные масштабы возмущений, когда

(10)
${{k}^{{ - 1}}} \gg {\chi \mathord{\left/ {\vphantom {\chi \upsilon }} \right. \kern-0em} \upsilon },\,\,\,\,h \approx {{h}_{{\upsilon }}} = {\chi \mathord{\left/ {\vphantom {\chi \upsilon }} \right. \kern-0em} \upsilon }.$

4. РЕШЕНИЕ

Исключая из системы уравнений все неизвестные, кроме одной, нетрудно получить уравнение

(11)
$\Delta _{2}^{3}w + \frac{{{{N}^{2}}}}{{\kappa \nu }}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} = \frac{{\beta g}}{\nu }\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}{{\Delta }_{2}}\mu = - \frac{{\beta g\upsilon }}{{\nu \chi }}\frac{{{{\partial }^{3}}\mu }}{{\partial {{x}^{2}}\partial z}},$
где $N = {{\left( {\alpha g\gamma } \right)}^{{{\text{1/2}}}}}$ – частота плавучести.

Для модели (7), (8) ищем решение в виде горизонтальной гармоники: $w = W\left( z \right)\cos \left( {kx} \right),$ u = = U(z)sin(kx) и т.д. Последнее уравнение принимает вид

(12)
${{\left( {\frac{{{{d}^{2}}}}{{d{{z}^{2}}}} - {{k}^{2}}} \right)}^{3}}W - \frac{1}{{h_{N}^{6}}}W = - \frac{{\beta g\upsilon {{k}^{2}}{{M}_{1}}}}{{\nu {{\chi }^{2}}}}\exp \left( { - \frac{z}{h}} \right),$
где ${{h}_{N}} = {{\left( {{{\kappa \nu } \mathord{\left/ {\vphantom {{\kappa \nu } {{{k}^{2}}{{N}^{2}}}}} \right. \kern-0em} {{{k}^{2}}{{N}^{2}}}}} \right)}^{{{\text{1/6}}}}}$ – вертикальный масштаб, определяемый фоновой температурной стратификацией. Общее решение (12) представляет собой сумму частного решения неоднородного уравнения (12) ${{W}_{p}}$ и общего решения однородного уравнения. С учетом (10),

(13)
$\begin{gathered} {{W}_{p}} \approx W{\text{*}}\exp \left( { - \frac{z}{h}} \right), \\ W{\text{*}} = {{ - \frac{{\beta g\upsilon {{k}^{2}}{{M}_{1}}}}{{\nu {{\chi }^{2}}}}} \mathord{\left/ {\vphantom {{ - \frac{{\beta g\upsilon {{k}^{2}}{{M}_{1}}}}{{\nu {{\chi }^{2}}}}} {\left( {\frac{1}{{{{h}^{6}}}} - \frac{1}{{h_{N}^{6}}}} \right)}}} \right. \kern-0em} {\left( {\frac{1}{{{{h}^{6}}}} - \frac{1}{{h_{N}^{6}}}} \right)}} \\ \end{gathered} $

(не рассматриваем здесь особый случай совпадения масштабов $h$ и ${{h}_{N}}$). Таким образом, с учетом условия затухания возмущений с высотой, решение уравнения (12) можно записать в виде

$W \approx W{\text{*}}\exp \left( { - \frac{z}{h}} \right) + \sum\limits_{j = 1}^3 {{{C}_{j}}\exp \left( {{{\sigma }_{j}}z} \right)} ,$
где ${{\sigma }_{j}}$ – корни характеристического уравнения однородного уравнения с отрицательными действительными частями, ${{C}_{j}}$ – постоянные интегрирования. Если ${{h}_{N}}$ много меньше горизонтального масштаба возмущений ${{k}^{{ - 1}}},$ то

${{\sigma }_{1}} \approx - h_{N}^{{ - 1}},\,\,\,\,{{\sigma }_{{2,3}}} \approx h_{N}^{{ - 1}}\exp \left( { \pm \frac{2}{3}\pi i} \right).$

Согласно нижним граничным условиям, постоянные интегрирования ${{C}_{j}}$ находятся из системы уравнений:

$\begin{gathered} \sum\limits_{j = 1}^3 {{{C}_{j}}} = - {{W}_{*}}{\text{,}}\,\,\,\,\sum\limits_{j = 1}^3 {{{\sigma }_{j}}{{C}_{j}}} = {{{{W}_{*}}} \mathord{\left/ {\vphantom {{{{W}_{*}}} h}} \right. \kern-0em} h}, \\ \sum\limits_{j = 1}^3 {{{{{C}_{j}}} \mathord{\left/ {\vphantom {{{{C}_{j}}} {\sigma _{i}^{2}}}} \right. \kern-0em} {\sigma _{i}^{2}}} = - {{W}_{*}}{{h}^{2}}} \\ \end{gathered} $

(в последнем уравнении учтено неравенство (10)).

5. АНАЛИЗ СЛУЧАЯ НЕЙТРАЛЬНОЙ ФОНОВОЙ СТРАТИФИКАЦИИ $N = 0,$ ${{h}_{N}} = \infty $

Этот предельный случай представляет особый интерес, поскольку позволяет получить мажорантную оценку для скорости рассматриваемых плотностных течений при отсутствии отрицательных обратных связей, обусловленных устойчивой стратификацией. При слабых фоновых температурных стратификациях плотностные течения не приводят к заметным температурным возмущениям и полностью определяются неоднородным полем концентрации оседающей примеси. В этом случае уравнение (12) имеет вид

${{\left( {\frac{{{{d}^{2}}}}{{d{{z}^{2}}}} - {{k}^{2}}} \right)}^{3}}W = - \frac{{\beta g\upsilon {{k}^{2}}{{M}_{1}}}}{{\nu {{\chi }^{2}}}}\exp \left( { - \frac{z}{h}} \right).$

С учетом (10), приближенное решение будет

(14)
$\begin{gathered} w \approx \frac{{\beta g{{k}^{2}}{{\chi }^{4}}{{M}_{1}}}}{{\nu {{\upsilon }^{5}}}} \times \\ \times \,\,\left\{ { - \exp \left( { - \frac{z}{h}} \right) + \left[ {1 - \left( {1 - hk} \right)\frac{z}{h}} \right]\exp \left( { - kz} \right)} \right\}\cos \left( {kx} \right), \\ u \approx \frac{{\beta gk{{\chi }^{3}}{{M}_{1}}}}{{\nu {{\upsilon }^{4}}}} \times \\ \times \,\,\left\{ { - \exp \left( { - \frac{z}{h}} \right) + \left[ {1 - \left( {1 - hk} \right)kz} \right]\exp \left( { - kz} \right)} \right\}\sin \left( {kx} \right). \\ \end{gathered} $

Порядки амплитуд возмущений можно оценить и непосредственно из простых физических соображений. Если слой оседающей примеси толщиной порядка $h \approx {\chi \mathord{\left/ {\vphantom {\chi \upsilon }} \right. \kern-0em} \upsilon },$ в котором возникают горизонтальные градиенты плотности, достаточно тонкий (выполняется (10)), то можно пользоваться приближением гидростатики: $\left| {p{\kern 1pt} '} \right|\sim g\left| {\rho {\kern 1pt} '} \right|h\sim \beta \bar {\rho }g\mu h\sim $ $\sim \beta \bar {\rho }g\chi {{M\left( x \right)} \mathord{\left/ {\vphantom {{M\left( x \right)} {{{\upsilon }^{2}}}}} \right. \kern-0em} {{{\upsilon }^{2}}}}.$ В этом приповерхностном слое среды в первом уравнении (2) существует приближенный баланс горизонтальной силы градиента давления $\left( {{1 \mathord{\left/ {\vphantom {1 {\bar {\rho }}}} \right. \kern-0em} {\bar {\rho }}}} \right)\left( {{{\partial p{\kern 1pt} '} \mathord{\left/ {\vphantom {{\partial p{\kern 1pt} '} {\partial x}}} \right. \kern-0em} {\partial x}}} \right)$ ~ ${{\beta g\chi k{{M}_{1}}} \mathord{\left/ {\vphantom {{\beta g\chi k{{M}_{1}}} {{{\upsilon }^{2}}}}} \right. \kern-0em} {{{\upsilon }^{2}}}}$ и силы вязкого трения ${{\nu {{d}^{2}}u} \mathord{\left/ {\vphantom {{\nu {{d}^{2}}u} {d{{z}^{2}}}}} \right. \kern-0em} {d{{z}^{2}}}}$ ~ ${{\nu u} \mathord{\left/ {\vphantom {{\nu u} {{{h}^{2}}}}} \right. \kern-0em} {{{h}^{2}}}}.$ Приравняв эти выражения, получаем для амплитуды $u$ выражение, согласующееся со вторым равенством (14). Предположение о гармонической зависимости возмущений от x при этом практически не использовалось, так что оно не играет принципиальной роли.

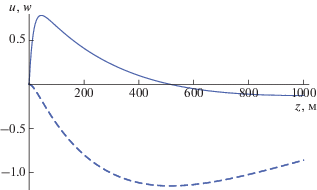
Пусть, например, в приземном слое воздуха в условиях приземной метели [7, 8] $\bar {\rho } = 1$ кг/м3, коэффициенты турбулентного обмена ν = κ = χ = 3 м2/с, $\upsilon = 0.2$ м/с, тогда $h \approx 15$ м. Если при этом амплитуда вариаций притока примеси ${{M}_{1}}$ составляет 10–2 кг/(м2 с) на горизонтальных масштабах порядка километра ($k = 2 \times {{10}^{{ - 3}}}$ м–1), $\beta = 1\,\,$ м3/кг, амплитуда горизонтальной скорости возникающих течений порядка 1 м/с, вертикальной – на два порядка меньше. Как видно из полученного решения, амплитуда этих течений сильно зависит от коэффициента диффузии примеси и особенно – от скорости оседания частиц. На рис. 1 приведены вертикальные зависимости двух составляющих скорости для рассмотренного численного примера. В области повышенного поступления и концентрации тяжелой примеси повышено гидростатическое давление, так что имеют место горизонтальное растекание среды и нисходящие движения. Хотя горизонтальная сила градиента давления, как упоминалось выше, действует в тонком слое толщиной порядка $h \approx {\chi \mathord{\left/ {\vphantom {\chi \upsilon }} \right. \kern-0em} \upsilon },$ как видно из рисунка, горизонтальное движение охватывает слой на порядок большей толщины (благодаря вязкости).

6. ЗАКЛЮЧЕНИЕ

Рис. 1.

Примеры профилей $u$ на вертикали $kx = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (сплошная линия, нормировано на ${{\beta gk{{\chi }^{3}}{{M}_{1}}} \mathord{\left/ {\vphantom {{\beta gk{{\chi }^{3}}{{M}_{1}}} {\left( {\nu {{\upsilon }^{4}}} \right)}}} \right. \kern-0em} {\left( {\nu {{\upsilon }^{4}}} \right)}}$) и $w$ на вертикали $x = 0$ (штриховая линия, нормировано на ${{10\beta g{{k}^{2}}{{\chi }^{4}}{{M}_{1}}} \mathord{\left/ {\vphantom {{10\beta g{{k}^{2}}{{\chi }^{4}}{{M}_{1}}} {\left( {\nu {{\upsilon }^{5}}} \right)}}} \right. \kern-0em} {\left( {\nu {{\upsilon }^{5}}} \right)}}$).

Явления, подобные пыльным бурям, метелям и т.п., вообще говоря, очень сложны [4, 7, 8], поскольку зависят от процессов разной физической природы и разных масштабов. В настоящей заметке рассмотрен лишь небольшой блок этого круга проблем: возникновение плотностных течений при заданном неоднородном поступлении в среду тяжелой примеси. Выше найдены закономерности таких течений в рамках простейшей аналитической модели. Полученные нетривиальные зависимости амплитуд от значений параметров хорошо согласуются с прозрачными физическими соображениями. Наиболее сильно амплитуда возникающих течений зависит от скорости оседания частиц. При прочих фиксированных параметрах, более “эффективно” поступление мелких, медленно оседающих частиц.

Использованное здесь линейное приближение применимо при выполнении условий типа u2$ \ll $ |p'|/$\bar {\rho }$ это приводит к условию βgk2χ5M1/ν2υ6) $ \ll $ 1 К близкому ограничению приводит и фактически использовавшееся предположение $\left| w \right| \ll \upsilon .$

Список литературы

  1. Gyr A., Hoyer K. Sediment Transport: A Geophysical Phenomenon. Berlin: Springer-Verlag, 2006. 286 c.

  2. Ungarish M. An Introduction to Gravity Currents and Intrusions. Boca Raton: CRC Press, 2009. 505 p.

  3. Ungarish M. Hydrodynamics of Suspensions Fundamentals of Centrifugal and Gravity Separation. Berlin: Springer-Verlag, 1993. 317 p.

  4. Голицын Г.С. Введение в динамику планетных атмосфер. Ленинград: Гидрометеоиздат, 1973. 104 с.

  5. Самолюбов Б.И. Придонные стратифицированные течения. М.: Научный мир, 1999. 434 с.

  6. Жмур В.В., Сапов Д.А. Катастрофические взвесенесущие гравитационные потоки. В кн.: Мировой океан. Т. 1. Геология и тектоника океана. Катастрофические явления в океане. М.: Научный мир, 2013. С. 499–524.

  7. Ингель Л.Х. Обобщение модели Прандтля на случай склоновых течений с тяжелой примесью // Прикладная механика и техническая физика. 2018. № 5. С. 104–108.

  8. Бычкова В.И. Параметризация процессов возникновения и эволюции низовой метели: Дис. … канд. физ.-мат. наук. М., 2016.

  9. UNEP, WMO, UNCCD. Global Assessment of Sand and Dust Storms. United Nations Environment Programme. Nairobi: Gemma Shepherd, 2016. 123 p.

  10. Ingel L.Kh., Belyaeva M.V. Toward the theory of convection in a rotating stratified medium over a thermally inhomogeneous horizontal surface // J. Eng. Phys. Thermophys. 2011. V. 84. № 4. P. 820–826.

  11. Гилл А.Е. Динамика атмосферы и океана. Т. 1. М.: Мир, 1986. 397 с.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал