Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 3, стр. 293-308

ВВЕДЕНИЕ

Моделирование отдельных акваторий (морей, заливов, открытых акваторий океана) и прибрежных территорий является одним из актуальных и развивающихся направлений математической геофизики. В частности, это связано с необходимостью оценки влияния антропогенного воздействия на окружающую среду. Для учета специфики рассматриваемой акватории и корректного воспроизведения физических явлений в ней недостаточно проведения расчетов по модели общей циркуляции Мирового океана. Однако, при создании моделей открытых акваторий необходимо решать проблему постановки граничных условий на жидких границах (под жидкой, или открытой границей будем понимать границу типа “вода–вода”, отделяющую рассматриваемую область от Мирового океана). От способа задания граничных условий на жидких границах напрямую зависит полученный результат как при долгосрочных расчетах, так и в задачах оперативного прогноза.

Существуют различные подходы к решению проблемы учета жидких границ в моделях гидротермодинамики открытых акваторий. Одним из подходов можно считать проведение расчета по всей акватории Мирового океана – на грубой сетке вне рассматриваемой акватории, на более мелкой – внутри: при этом существенно возрастают вычислительные затраты, однако отсутствуют внешние жидкие границы. Иногда результаты расчетов по всей акватории Мирового океана на грубой сетке используются для задания граничных условий на жидкой границе. Развитием данных идей является метод вложенных сеток – с обратной связью, с неполной обратной связью и без обратной связи [1]. Еще одним распространенным приемом является использование осредненных данных о потоках через жидкую границу [2] или задание потоков с помощью данных наблюдений [3]. Отдельный цикл работ [4, 5] посвящен формулировке условий излучения на жидких границах и их модификаций применительно к моделям гидродинамики. Также, перспективным методом для решения проблемы постановки граничных условий на жидкой границе можно считать ассимиляцию данных.

Существует множество работ, рассматривающих различные методы вариационной ассимиляции данных применительно к задачам моделирования океанов и морей [6–10]. В работе [6] приведен обзор известных исследований по данной тематике. Ассимиляция данных является процедурой, смысл которой – сблизить получаемый в результате моделирования результат с данными наблюдений. Модели, в которых ассимиляция данных не используется, чаще всего дают статистически правильное решение, но при попытке сравнить данные наблюдений и полученный результат в определенный момент времени можно наблюдать значительные отличия между ними. Причиной таких противоречий является то, что общие модели циркуляции океана, которые часто используются для морских регионов горизонтального масштаба более 10 км, учитывают только общий эффект от тех явлений, масштаб которых по пространству значительно меньше масштаба рассматриваемой акватории [11]. Отличия также могут быть вызваны ошибками в задании начальных, граничных условий и внешних данных об атмосфере, ошибками в численном решении уравнений на сетке. Более того, моделируемые эффекты существенно нелинейны, что приводит к тому, что ошибки могут расти со временем и отдалять решение от данных наблюдений [6]. Методы вариационной ассимиляции предоставляют математическую оценку того, как требуется изменить вектор управления (в который могут входить различные параметры модели – коэффициенты, “форсинги”, начальные и граничные условия, известные неточно), чтобы получить решение, максимально близкое к данным наблюдений. Следует заметить, что полученный таким образом вектор управления может принимать физически необоснованные значения. Такое может случаться из-за того, что реальные данные наблюдений отражают все происходящие в природе явления, в том числе и те, которые не учитываются в математической модели. Для решения данного противоречия в работе [12] был предложен вариационный подход, идея которого заключается в том, что не только сами функции в граничных условиях заданы неточно, но и сами граничные условия и даже уравнения модели сформулированы “грубо”. Суть предложенного в [12] метода состоит в том, чтобы отыскать обобщенное решение в смысле наименьших квадратов, минимизирующее функционал невязки, в который с подобранными весами входят также слагаемые, отвечающие за близость к данным наблюдений.

Идея метода, предложенного в работах [13–17] состоит в том, чтобы, имея данные наблюдений в некоторый момент времени, рассматривать задачу как обратную, в которой дополнительными неизвестными являются функции потоков через открытую границу. В работе [16] сформулирован класс обратных задач и задач вариационной ассимиляции данных наблюдений, связанных с математическим моделированием гидрофизических полей в акваториях (морях и океанах) при наличии жидких границ, в применении к модели гидротермодинамики, основанной на системе уравнений в приближении Буссинеска и гидростатики [18, 19]. Для аппроксимации модели по времени был использован метод расщепления, что позволило рассматривать задачу ассимиляции данных для нелинейной модели гидротермодинамики на каждом интервале по времени, решая последовательно более простые задачи ассимиляции, привлекая соответствующие изменяющимся переменным данные наблюдений. Был поставлен класс обратных задач о “граничных функциях”, определяющих граничные условия на жидких границах и была исследована разрешимость ряда задач из этого класса, а также предложены алгоритмы их численного решения на основе вариационной ассимиляции данных наблюдений. В работе [14] была исследована обратная задача об определении неизвестной функции в граничных условиях на жидкой границе для простейшей модели приливов. Результаты работы были использованы в [20], где приведены результаты численных экспериментов применительно к акватории Охотского моря. В работе [15] обратные задачи с ассимиляцией данных об уровне моря из [16] были переформулированы и исследованы как обратные задачи для эволюционных уравнений второго порядка.

В настоящей работе приведена формулировка общей задачи вариационной ассимиляции данных наблюдений для модели гидротермодинамики открытой акватории, основанной на методе расщепления. Сформулирован алгоритм вариационной ассимиляции данных о температуре на жидкой границе, прведены результаты численных экспериментов по использованию алгоритма в модели гидротермодинамики Балтийского моря [18] в сравнении с алгоритмом, рассмотренным в работе [21]. Сформулирован алгоритм вариационнной ассимиляции данных об уровне на жидкой границе, приведены результаты численных экспериментов по ассимиляции данных наблюдений со спутников и уровнемерных постов в модели [18].

1. ПОСТАНОВКА ЗАДАЧИ

В данном разделе вводятся основные обозначения и уравнения, которые используются в рассматриваемых задачах, а также формулируется класс обратных задач и задач вариационной ассимиляции данных наблюдений, связанных с математическим моделированием гидрофизических полей в акваториях (морях и океанах) при наличии жидких границ, в применении к модели гидротермодинамики, основанной на системе уравнений в приближении Буссинеска и гидростатики.

1.1. Рассмотрим географическую (геодезическую) систему координат ($\lambda ,\theta ,r$), где $\lambda \in [0,\,2\pi ]$ – географическая долгота, увеличивающаяся с запада на восток, $\theta \in [{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2},\,\pi {\text{/}}2]$ – географическая широта, растущая с юга на север, $r$ – расстояние точки от центра Земли, средний радиус которой принимается равным ${{R}_{{\text{З}}}}.$ Вместо $r$ введем координату $z = {{R}_{З}} - r$ оси $Oz,$ направленной по нормали от поверхности сферы ${{S}_{R}}$ радиуса ${{R}_{{\text{З}}}}$ к еe центру, т.е. по направлению силы тяжести. Единичные вектора в $\lambda $-, $\theta $- и $z$-направлениях обозначим соответственно через ${{e}_{\lambda }},$ ${{e}_{\theta }},$ ${{e}_{z}}.$ Тогда вектор скорости в океане записывается в форме: $\vec {U} = u{{e}_{{\lambda }}} + {v}{{e}_{{\theta }}}$ + $w{{e}_{z}} \equiv (\vec {u},w),$ где $\vec {u} = (u,{v})$ – “горизонтальный вектор” скорости в координатной форме, а $w$ – “вертикальная скорость”.

Обозначим через $\Omega $ часть поверхности сферы ${{S}_{R}},$ которую будем называть также “поверхностью отсчета”. Поверхность океана будем задавать уравнением $z = \xi (\lambda ,\theta ,t),$ где ($\lambda ,$ $\theta ,$ ${{R}_{З}}$) $ \in \Omega ,$ а $t$ – временная переменная, $t \in $ [0, $\bar {t}$] ($\bar {t}$ < $\infty )$. Функцию рельефа дна определим как $z = H(\lambda ,\theta )$ при ($\lambda $,$\theta $,${{R}_{{\text{З}}}}$) ∈ $\Omega ,$ где $H(\lambda ,\theta ) \geqslant \epsilon ,$ $\epsilon = {\text{const}} > 0.$

В дальнейшем мы будем использовать также следующие обозначения: $\lambda \equiv x,$ $\theta \equiv y,$ $\vec {x} \equiv (x,y,z).$ Элемент объeма в области $D(t){\text{:}}$ D(t) = {(x, y, z) : (λ, θ, R_З) ∈ Ω, $\xi (\lambda ,\theta ,t) < z < H(\lambda ,\theta ){\text{\} }},$ $t \in [0,\bar {t}],$ есть $dD = {{(R - z)}^{2}}cosydxdydz,$ а элемент поверхности $\Omega $ имеет вид $d\Omega = R_{{\text{З}}}^{2}cosydxdy.$ Введем следующие дифференциальные операции градиента, дивергенции и полной производной в одной из сферических систем координат при $r \equiv r(z) \equiv R - z \cong R,$ $n \equiv 1{\text{/}}r,$ $m \equiv {1 \mathord{\left/ {\vphantom {1 {(rcosy)}}} \right. \kern-0em} {(rcosy)}}$ (оставив за этими операциями известные обозначения из векторного анализа):

Далее используются также следующие дифференциальные операторы второго порядка: ${{A}_{\Phi }}\Phi $ ≡ ≡ $ - {\mathbf{Div}}({{a}_{\Phi }}{\mathbf{Grad}}{\Phi }),$ где ${{a}_{\Phi }} = diag({{({{a}_{\Phi }})}_{{ii}}}),$ (a_Ф)₁₁ = = ${{({{a}_{\Phi }})}_{{22}}} \equiv {{\mu }_{\Phi }},$ ${{({{a}_{\Phi }})}_{{33}}} \equiv {{\nu }_{\Phi }},$ а индекс $\Phi $ может принимать значения u, v, T, S (т.е. обозначения компонентов вектора горизонтальной скорости, температуры $T$ и солeности $S)$. Принимается также: ${{\mu }_{u}} = {{\mu }_{v}} \equiv \mu ,$ ${{\nu }_{u}} = {{\nu }_{v}} \equiv \nu $ и предполагается, что $\mu ,$ $\nu ,$ ${{\mu }_{T}},$ ${{\mu }_{S}},$ ${{\nu }_{T}},$ ${{\nu }_{S}}$ являются заданными положительными и гладкими функциями. Далее будет рассматриваться также оператор четвертого порядка ${{({{A}_{k}})}^{2}},$ где оператор второго порядка ${{A}_{k}}$ введен выше при ${{A}_{\varphi }} = {{A}_{k}}$ и определяется матрицей $\hat {k} = diag{\text{\{ }}{{k}_{{ii}}}{\text{\} }}$ с неотрицательными диагональными элементами ${{k}_{{ii}}},$ являющимися постоянными или достаточно гладкими функциями. В последующем через $l = l(y)$ обозначается Кориолисов параметр: $l = 2\omega siny,$ где $\omega $ – угловая скорость вращения Земли, а также $f(u) = l$ + $musiny \equiv l + {{f}_{1}}(u).$

Заметим, что функция уровня $\xi = \xi (x,y,t)$ является также одной из неизвестных функций, подлежащих определению, поэтому область $D(t)$ является областью с неизвестной границей (или областью с движущейся границей). Рассмотрим также фиксированную область: D = = ${\text{\{ }}(\lambda ,\theta ,z):{\mkern 1mu} \;(\lambda ,\theta ,{{R}_{{\text{З}}}}) \in \Omega ,$ $0 < z < H(\lambda ,\theta ){\text{\} }}.$ Границу области $\Gamma \equiv \partial D$ мы будем представлять как объединение четырeх непересекающихся частей, ${{\Gamma }_{S}},$ ${{\Gamma }_{{w,op}}},$ ${{\Gamma }_{{w,c}}},$ ${{\Gamma }_{H}},$ где ${{\Gamma }_{S}} \equiv \Omega $ – “невозмущeнная поверхность океана”, ${{\Gamma }_{{w,op}}}$ – жидкая (открытая) часть вертикальной боковой границы, ${{\Gamma }_{{w,c}}}$ – твeрдая часть вертикальной боковой границы, ${{\Gamma }_{H}}$ – дно океана. Характеристические функции ${{\Gamma }_{S}},$ ${{\Gamma }_{{w,op}}},$ ${{\Gamma }_{{w,c}}},$ ${{\Gamma }_{H}}$ – частей границы $\Gamma $ будем обозначать соответственно ${{m}_{S}},$ ${{m}_{{w,op}}},$ ${{m}_{{w,c}}},$ ${{m}_{H}}.$ Отметим, что некоторые из частей ${{\Gamma }_{S}},$ ${{\Gamma }_{{w,op}}},$ ${{\Gamma }_{{w,c}}},$ ${{\Gamma }_{H}}$ могут отсутствовать.

В дальнейшем мы всегда предполагаем, что $\Omega $ является многосвязным многообразием на ${{S}_{R}},$ а границы $\partial \Omega ,$ $\Gamma $ считаем кусочно-гладкими класса ${{C}^{{(2)}}},$ локально удовлетворяющими условию Липшица. Единичный вектор внешней нормали к $\Gamma $ обозначаем через $\overrightarrow N \equiv $(${{N}_{1}},$ ${{N}_{2}},$ ${{N}_{3}}$). Отмечаем, что $\vec {N}$ = (0, 0, –1) на ${{\Gamma }_{S}}$ и $\vec {N}$ = (${{N}_{1}},$ ${{N}_{2}},$ 0) на ${{\Gamma }_{w}} = {{\Gamma }_{{w,op}}} \cup {{\Gamma }_{{w,c}}}$ при этом вектор $\vec {n}$ ≡ (${{N}_{1}},$ ${{N}_{2}})$ ≡ (${{n}_{1}},$ ${{n}_{2}})$ является единичным вектором внешней нормали к $\partial \Omega .$ Выражение компонентов ${{N}_{1}},$ ${{N}_{2}},$ ${{N}_{3}}$ определяется выбираемым параметрическим представлением той или иной части границы.

При рассмотрении вектора скорости на границе $\Gamma $ мы будем обозначать его составляющую по нормали через ${{U}_{n}}{\text{:}}$ ${{U}_{n}}$ = $\vec {U} \cdot \vec {N} = u{{N}_{1}}$ + $v{{N}_{2}} + w{{N}_{3}}.$ И пусть далее

Отмечаем, что ${{U}_{n}} = U_{n}^{{( + )}}$ – $U_{n}^{{( - )}}$ на $\Gamma .$

1.2. Запишем в области $D$ в переменных $(\lambda ,\theta ,z)$ при $t \in (0,\bar {t})$ систему уравнений гидротермодинамики в приближении Буссинеска и гидростатики [22], но беря коэффициенты Ламе соответствующими сферической системе координат [16, 23]:

где

$\vec {f} = ({{f}_{1}},{{f}_{2}}),$ ${{f}_{T}},{\mkern 1mu} $ ${{f}_{S}},$ ${{f}_{P}}$ – заданные функции “внутренних” источников, $g = {\text{const}} > 0,$ ${{\rho }_{0}},$ ${{T}^{{(0)}}},$ ${{S}^{{(0)}}}$ – “невозмущенные” значения плотности воды, температуры, солености, ${{\beta }_{T}},$ ${{\beta }_{S}}$ – коэффициенты (считающиеся постоянными), ${{\beta }_{{TS}}}(T,S),$ ${{P}_{a}}$ – заданные функции, а $\gamma $ – числовой параметр. Здесь и в дальнейшем используется следующая весовая функция: $\Theta (z) \equiv {{r(z)} \mathord{\left/ {\vphantom {{r(z)} R}} \right. \kern-0em} R}.$ В дальнейшем рассматривается случай, когда $\vec {f} \equiv g{\mathbf{grad}}G$ при некоторой скалярной функции $G = G(\lambda ,\theta ,t),$ например, $G \equiv {{\xi }^{ + }}$ – статический прилив, более детальное описание которого дано в [23].

Обратим внимание на то, что по физическому смыслу координаты $(\lambda ,\theta ,z)$ являются геодезическими, но в силу приближенной записи коэффициентов Ламе система (1) принимает вид в одной из систем сферических координат [16].

При рассмотрении (1) в $D \times (0,\bar {t})$ можно задавать следующие граничные и начальные условия [16].

Граничные условия на ${{\Gamma }_{S}}{\text{:}}$

где $\tau _{x}^{{(a)}},$ $\tau _{y}^{{(a)}}$ – компоненты векторов касательных напряжений ветра соответственно вдоль осей Ox и Oy на поверхности $z = 0,$ ${{\gamma }_{T}},$ ${{\gamma }_{S}},$ ${{T}_{a}},$ ${{S}_{a}},$ – заданные функции, ${{Q}_{T}},$ ${{Q}_{S}}$ – функции потоков, заданные на всей $\Gamma .$

Граничные условия на ${{\Gamma }_{{w,c}}}$ (на “твердой боковой стенке”):

где ${{\tau }_{w}}$ = ($ - {{N}_{2}},$ ${{N}_{1}},$ 0), $\tilde {U} \equiv (u,{v},0) \equiv (\vec {u},0),$ ${\varphi \mathord{\left/ {\vphantom {\varphi {\partial {{N}_{{\varphi }}}}}} \right. \kern-0em} {\partial {{N}_{{\varphi }}}}} \equiv \vec {N} \cdot \mathop {\hat {a}}\nolimits_\varphi \cdot {\mathbf{Grad}}\varphi ,$ $\varphi = u,{v},T,S.$

Граничные условия на ${{\Gamma }_{{w,op}}}$ (на “жидкой части боковой стенки”):

Граничные условия на ${{\Gamma }_{H}}$ (“на дне”):

где ${{\tau }_{x}},$ ${{\tau }_{y}}$ – система единичных ортогональных касательных векторов на поверхности $z = 0;$ $\tau _{x}^{{(b)}},$ $\tau _{y}^{{(b)}}$ – проекции вектора напряжения придонного трения соответственно на оси Ox, Oy.

Начальные условия для u, v, T, S, $\xi {\text{:}}$

где ${{u}^{0}},$ ${{{v}}^{0}},$ ${{T}^{0}},$ ${{S}^{0}},$ ${{\xi }^{0}}$ – заданные функции.

Пусть функции $d,$ ${{d}_{s}},$ ${{d}_{T}},$ ${{d}_{S}},$ ${{f}_{3}}$ заданы. Тогда задача крупномасштабной динамики океана в терминах функций $u,$ ${v},$ $\xi ,$ $T,$ $S$ формулируется так: найти u, v, $\xi $, T, S, удовлетворяющие (1)–(6).

Заметим, что “диффузионные операторы” в уравнениях для $u,$ ${v}$ не учитывают некоторых дифференциальных операторов меньших порядков, существенных около полюсов. Поэтому, вообще говоря, система (1) должна рассматриваться в области с исключенными точками полюсов. В настоящей работе ограничимся рассмотрением системы уравнений (1).

Для аппроксимации задачи (1)–(6) по времени используется метод расщепления. Пусть на $[0,\bar {t}]$ введена сетка: $0 = {{t}_{0}} < {{t}_{1}} < $ … $ < {{t}_{{J - 1}}} < {{t}_{J}} = \bar {t},$ $\Delta {{t}_{j}} = {{t}_{j}} - {{t}_{{j - 1}}}.$ Приведем одну из схем, полученную методом слабой аппроксимации, аппроксимирующую исходную задачу, рассматривая подзадачи, входящие в эту схему, в “классических постановках” и считая все компоненты решений обладающими необходимой гладкостью по всем независимым переменным. Эта схема состоит из шагов (этапов), перечисленных ниже. При формулировке шагов используются индексы: нижний индекс у отыскиваемых переменных ($T,$ $\xi $ и др.) обозначает номер шага метода расщепления, а верхний индекс – номер шага по времени.

ШАГ 1: Решение $j$-ой подзадачи на этом шаге метода расщепления удовлетворяет системе соотношений вида (при $\vec {u}_{1}^{j} \equiv \vec {u},...,$ $\xi _{1}^{j} \equiv \xi $):

где ${{\vec {u}}^{0}} = ({{u}^{0}},{{{v}}^{0}}),\,\,\,\,\vec {u}_{5}^{{j - 1}} = \left( {u_{5}^{{j - 1}},\,\,{v}_{5}^{{j - 1}}} \right).$

Из (7) заключаем, что для этой задачи имеем:

Отыскание же $\vec {u},$ $\xi $ сводится к решению задач вида:

где

и решению следующей задачи:

Решая (9), (10) получаем $\xi = \xi _{1}^{j},$ а также

что заканчивает реализацию этого шага метода расщепления.

ШАГ 2. Решение $j$-ой подзадачи здесь удовлетворяет системе вида (при $\vec {u} \equiv \vec {u}_{2}^{{j - 1}},...,$ $\xi \equiv \xi _{2}^{j}$):

где $\vec {U} \equiv {{\vec {U}}^{j}}$ = $({{u}^{j}},{{{v}}^{j}},{{w}^{j}}),$ $U_{n}^{{\left( - \right)}}$ вычисляется на основе ${{\vec {U}}^{j}},$ а ${{\lambda }_{T}}$ и ${{\lambda }_{S}}$ есть заданные достаточно малые постоянные, вводимые для обоснования схемы расщепления (см. [16]).

Отмечаем, что в данной подзадаче имеем:

и после решения задачи для $T \equiv T_{2}^{j}$ вычисление $\vec {u} \equiv \vec {u}_{2}^{j}$ осуществляется по формуле:

Таким образом, реализация данного шага фактически сводится к решению подсистемы уравнений с целью вычисления $T \equiv T_{2}^{j}.$

ШАГ 3. Данный этап аналогичен предыдущему и он сводится к решению задачи для $S \equiv S_{3}^{j}{\text{:}}$

После чего полагается:

Функции $\vec {U},$ $U_{n}^{{( - )}}$ определяются так же, как и на предыдущем шаге.

ШАГ 4. Решаемая здесь подзадача имеет вид:

ШАГ 5. Система уравнений, соответствующая данному этапу решения задачи, имеет вид (при $\vec {u} \equiv \vec {u}_{5}^{j},...,$ $\xi \equiv \xi _{5}^{j}$):

где ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau } }^{{(a)}}} = \left( {\tau _{x}^{{(a)}},\tau _{y}^{{(a)}}} \right),$ ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau } }^{{(b)}}} = \left( {\tau _{x}^{{(b)}},\tau _{y}^{{(b)}}} \right),$ $\tilde {U} \equiv \tilde {U}_{4}^{j}$ = = $\left( {u_{4}^{j},{v}_{4}^{j},0} \right)$ а $\vec {U},$ $U_{n}^{{\left( - \right)}}$ определяются так же, как и ранее.

2. ЗАДАЧА ВАРИАЦИОННОЙ АССИМИЛЯЦИИ ДАННЫХ О ТЕМПЕРАТУРЕ

В данном разделе формулируется задача вариационной ассимиляции данных о температуре на жидкой границе и алгоритм ее решения, а также приводятся результаты численных экспериментов по использованию алгоритма в модели гидротермодинамики Балтийского моря.

Запишем задачу переноса–диффузии тепла (12) с Шага 2 метода расщепления в следующем виде:

где ${{f}_{T}},$ ${{\gamma }_{T}},$ ${{T}_{a}},$ ${{Q}_{F}}$ – заданные функции, ${{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial {{N}_{T}}}}} \right. \kern-0em} {\partial {{N}_{T}}}} \equiv \vec {N} \cdot {{\hat {a}}_{T}} \cdot {\mathbf{Grad}}T,$ ${{\gamma }_{T}} \equiv 0,$ ${{T}_{a}} \equiv 0$ на $\Gamma {\kern 1pt} \setminus {\kern 1pt} {{\Gamma }_{S}}$ $\forall t \in ({{t}_{{j - 1}}},{{t}_{j}}),$ $\quad U_{n}^{{( - )}} = 0$ на $({{\Gamma }_{{w,c}}} \cup {{\Gamma }_{H}} \cup {{\Gamma }_{S}})$ × × $({{t}_{{j - 1}}},{{t}_{j}}),$ $\quad {{d}_{T}} \equiv 0$ на $(\Gamma {\kern 1pt} \setminus {\kern 1pt} {{\Gamma }_{{w,op}}})$ × $({{t}_{{j - 1}}},{{t}_{j}}).$ После решения данной задачи функция ${{T}_{j}}$ принимается в качестве приближения к компоненту $T$ (температуре) точного решения на $D \times ({{t}_{{j - 1}}},{{t}_{j}}).$

Предположим, что на какой-то части ${{\Gamma }_{{o,T}}}$ границы $\Gamma = \partial D$ почти при всех $t \in ({{t}_{{j - 1}}},{{t}_{j}})$ имеются данные наблюдений за температурой, которые обозначим через ${{T}_{{obs}}}.$ Тогда, рассматривая функцию ${{d}_{T}}$ как дополнительную неизвестную (или как функцию, известную приближенно и требующую уточнения), можно сформулировать задачу ассимиляции данных о температуре на данном шаге схемы расщепления как обратную задачу, т.е. как задачу об отыскании $T$ и ${{d}_{T}},$ удовлетворяющих системе (23) и уравнению замыкания:

где ${{\chi }_{T}}$ – характеристическая функция границы ${{\Gamma }_{{o,T}}} \subseteq \Gamma .$

Для приближенного решения обратной задачи переформулируем ее как задачу минимизации функционала:

где $T = T({{d}_{T}})$ является решением задачи (23), а $\alpha $ – малый неотрицательный параметр, который имеет смысл параметра регуляризации А.Н. Тихонова [25].

Если ${{\Gamma }_{{o,T}}}$ совпадает с ${{\Gamma }_{{w,op}}},$ можно показать [21, 26], что обратная задача (23), (24) однозначно и плотно разрешима. В этом случае на основании теории, приведенной в [24], можно утверждать, что для приближенного решения задачи (23), (24) достаточно построить приближенное решение задачи (25) при малом $\alpha > 0.$ Вводя сопряженную задачу, запишем метод градиентного спуска для решения экстремальной задачи (25):

Вследствие плотной разрешимости задачи при ${{\Gamma }_{{w,op}}} = {{\Gamma }_{{o,T}}}$ при достаточно малом ${{\tau }_{k}} = \tau = {\text{const}} > 0$ имеем [24]:

Более того, если существует решение ${{d}_{T}},$ $T$ обратной задачи (23), (24), то оно единственно. При этом справедливо следующее утверждение о сходимости алгоритма (26)–(28):

При выполнении условий плотной разрешимости $inf{{J}_{\alpha }} \cong 0$ при $\alpha \to + 0$ и можно принять [24]:

– “оптимальный набор” параметров итерационного процесса в данной задаче при $\alpha \cong + 0.$

Приведем результаты численных экспериментов применительно к реальной морской акватории. Алгоритм (26)–(28) был внедрен в модель гидротермодинамики Балтийского моря [18] и использовался в расчетах на каждом втором временном слое модели на Шаге 2 метода расщепления, описанного выше. Были проведены расчеты гидротермодинамики Балтийского моря на временной интервал с 1 по 30 апреля 2007 г. следующего типа: расчет без использования процедуры ассимиляции, расчет с использованием ассимиляции (26)–(28) и расчет с использованием процедуры ассимиляции, описанной в работе [21]. Отличие процедуры ассимиляции, описанной в данной работе, от процедуры, представленной в работе [21], в форме записи граничного условия. Так, в алгоритме (26)–(28) ассимиляция данных проводится на всей жидкой границе, тогда как в работе [21] – только на той части границы, где нормальная составляющая скорости направлена внутрь области. В качестве данных наблюдений были использованы данные реанализа по модели HIROMB (High-Resolution Operational Model for the Baltic) версии 3.0, предоставляемые Шведским институтом гидрологии и метеорологии (SMHI). Данные были скачаны с сайта [27].

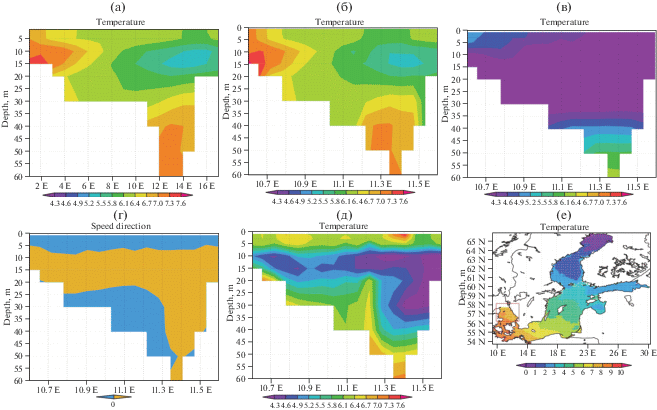
На рис. 1a представлено поле температуры ${{T}_{{obs}}}$ по данным реанализа с сайта [27] (разрез по глубине на открытой границе между Северным и Балтийским морем, положение самой границы можно увидеть на рис. 1е) 7 апреля 2007 г., которые были использованы в качестве данных наблюдений, на рис. 1б и 1в – поля температуры на момент времени 7 модельных суток с начала расчета с использованием и без использования процедуры ассимиляции (26)–(28) соответственно. На рис. 1г голубым цветом отмечены точки, где вектор скорости течения воды направлен внутрь акватории (из Северного моря в Балтийское). На рис. 1д – поле температуры на жидкой границе по результатам расчета с использованием ассимиляции из [21]. Из рисунков видно, что разработанный алгоритм (26)–(28) сближает результат расчета модели и данные на открытой границе, в то время как алгоритм [21] – только на той части границы, где нормальная составляющая скорости направлена внутрь области.

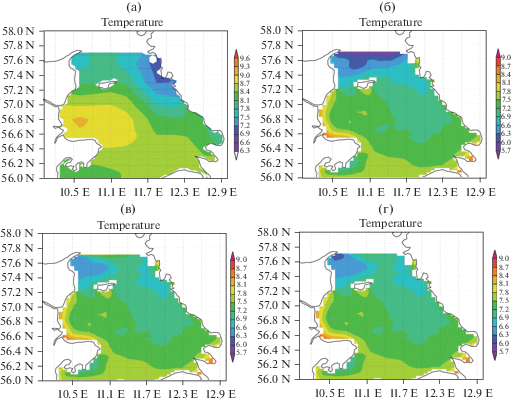
На рис. 2 для сравнения представлены распределения температуры по глубине 27 апреля 2007 г. на широте 57.4°: данные реанализа по модели HIRO-MB (рис. 2а), результаты расчета без использования ассимиляции (рис. 2б), с использованием ассимиляции (26)–(28) (рис. 2в), с использованием ассимиляции [21] (рис. 2г). По рисункам видно, что алгоритм ассимиляции приближает результаты расчета к данным реанализа не только на жидкой границе, где производится ассимиляция, но и на других вертикальных разрезах. Тем не менее, построение распределений температуры на разрезах, отстоящих от жидкой границы дальше, чем представленный на рис. 2, показало, что алгоритм ассимиляции (26)–(28) практически не оказывает влияния на распределение температуры по глубине южнее 56° северной широты. Это может быть связано с небольшим промежутком расчета (1 мес.). Необходимо дальнейшее исследование влияния рассматриваемого алгоритма на распределения температуры по глубине на различных широтах, полученные по результатам моделирования, для более длительных расчетов.

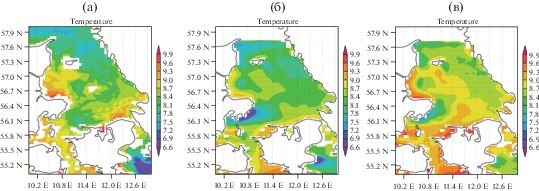
На рис. 3б, 3в, 3г представлены среднесуточные распределения температуры поверхности по результатам моделирования 14 апреля 2007 г: на рис. 3б – результаты расчета без использования ассимиляции, на рис. 3в – с использованием ассимиляции (26)–(28), на рис. 3г – с использованием ассимиляции [21]. Эти распределения можно сравнить с результатом интерполяции на сетку модели данных наблюдений со спутников [28, 29], представленным на рис. 3а. Как можно заметить, поле температуры на рис. 3в ближе к представленному на рис. 3а, чем поля температуры на рис. 3б, 3г. Разница между рис. 3в и 3г не так велика и сосредоточена вблизи жидкой границы. Заметим, что в проведенных экспериментах ассимиляция данных о температуре поверхности моря не проводилась, поэтому результаты моделирования, представленные на рис. 3б–3г, отличаются от данных наблюдений со спутников.

Дополнительно для сравнения алгоритмов ассимиляции представлены среднесуточные распределения температуры по поверхности 18 апреля 2007 г. по результатам моделирования за март–апрель 2007 г. с использованием алгоритма (26)–(28) (рис. 4б) и с использованием алгоритма [21] (рис. 4в). На рис. 4а показано среднесуточное распределение температуры, полученное из реанализа по модели NEMO-Nordic [30, 27 ] института SMHI. Сетка модели NEMO-Nordic охватывает акватории Балтийского и Северного морей, а также в данной модели реализована ассимиляция температуры поверхности моря и профилей температуры и солености по глубине. Тем не менее, принципы построения модели NEMO совершенно иные, поэтому распределения, представленные на рис. 4, отличаются.

На основании результатов численных экспериментов можно сделать следующие выводы. Разработанный алгоритм действительно успешно сближает результат расчета модели и данные на открытой границе, что подтверждает полученные теоретические результаты. При краткосрочных расчетах эффект от ассимиляции проявляется только в области вблизи открытой границы. Алгоритм оказывает слабое влияние на распределения температуры по глубине, и это влияние тем больше, чем дольше проводится расчет с ассимиляцией. Необходимо дальнейшее исследование влияния рассматриваемого алгоритма на распределения температуры по глубине на различных широтах, полученные по результатам моделирования, для более длительных расчетов. Эффективность использования алгоритма зависит от качества данных наблюдений. В данной работе в качестве данных наблюдений были использованы данные реанализа из Шведской модели гидротермодинамики Северного и Балтийского морей – эти данные имелись на каждые 6 ч и обладали достаточной гладкостью. Эксперименты с другими данными не проводились.

3. ЗАДАЧА ВАРИАЦИОННОЙ АССИМИЛЯЦИИ ДАННЫХ ОБ УРОВНЕ

Рассмотрим задачу (7) с Шага 1 метода расщепления. Как уже было сказано ранее, решение данной задачи можно свести к независимому решению задач (9) и (10), причем найденная в задаче (9) функция уровня $\xi \equiv \xi _{1}^{j}$ не изменяется ни в задаче (10), ни на других шагах метода расщепления, то есть ${{\xi }^{j}} = \xi _{5}^{j} = \xi _{1}^{j}.$ Поэтому ассимиляция данных об уровне должна производиться непосредственно в задаче (9).

Пусть далее функция ${{d}_{s}}$ является дополнительной неизвестной (управлением), которую необходимо определить посредством процедуры ассимиляции данных. Пусть также на некоторой части границы $\partial \Omega $ на интервале времени $({{t}_{{j - 1}}},{{t}_{j}})$ имеются данные наблюдений ${{\xi }_{{obs}}}$ за уровнем моря. Обозначим через ${{\chi }_{{\xi ,\partial \Omega }}}$ характеристическую функцию множества, где задана ${{\xi }_{{obs}}}.$ Сформулируем условие замыкания:

Запишем неявную схему аппроксимации задачи (9) на интервале $({{t}_{{j - 1}}},{{t}_{j}}),$ $\tau = {{t}_{j}} - {{t}_{{j - 1}}},$ по времени, и получим полудискретную задачу, являющуюся приближением к (9):

где $\bar {F} = {{({{f_{1}^{j} + {{u}^{{j - 1}}}} \mathord{\left/ {\vphantom {{f_{1}^{j} + {{u}^{{j - 1}}}} \tau }} \right. \kern-0em} \tau },\,\,{{f_{2}^{j} + {{{v}}^{{j - 1}}}} \mathord{\left/ {\vphantom {{f_{2}^{j} + {{{v}}^{{j - 1}}}} \tau }} \right. \kern-0em} \tau },\,\,{{{{\xi }^{j}}} \mathord{\left/ {\vphantom {{{{\xi }^{j}}} \tau }} \right. \kern-0em} \tau })}^{T}},$ $\tilde {\bar {f}}$ = = $({{(\bar {F})}_{1}},{{(\bar {F})}_{2}}){{)}^{T}}$ ≡ $({{\tilde {f}}_{1}},{{\tilde {f}}_{2}}).$ Таким образом, обратная задача формулируется следующим образом: найти $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{U} ,$ $\xi $ и ${{d}_{s}},$ такие, что выполняются (31), (30).

Переформулируем задачу как задачу оптимального управления. Для этого введем функционал:

где $d_{s}^{{(0)}}$ – заданная функция. Задача оптимального управления формулируется следующим образом: найти функцию ${{d}_{s}},$ доставляющую минимум функционалу ${{J}_{{\alpha }}},$ такую, что выполняется (31).

Теоретическое исследование обратной задачи (31), (30) было проведено в работе [14]. Для теоретического исследования система (31) была сведена к эллиптической третьей краевой задаче для $\xi ,$ после чего была введена обобщенная постановка задачи, получены условия однозначной и плотной разрешимости (в частности, если данные наблюдений заданы на жидкой границе, задача однозначно и плотно разрешима). Задачу минимизации функционала ${{J}_{{\alpha }}}$ можно решать, например, с помощью метода градиентного спуска, который будет иметь вид следующего итерационного процесса (для системы, сведенной к полудискретной форме):

где $k$ – номер итерации. Вследствие плотной разрешимости задачи в случае, когда данные наблюдений заданы на жидкой границе, при достаточно малом ${{\tau }_{k}} = \tau = {\text{const}} > 0$ имеем [24]:

Также в этом случае параметр итерационного процесса можно вычислять, пользуясь следующей формулой (см. [24]):

Отдельного внимания заслуживает вопрос о доступности реальных данных наблюдений. Как было показано [14], если данные наблюдений заданы на всей жидкой границе, задача однозначно и плотно разрешима и итерационный процесс сходится, причем функции ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{U} }_{k}}(\alpha ),$ ${{\xi }_{k}}(\alpha ),$ ${{({{d}_{s}})}_{k}}(\alpha )$ при достаточно малом $\alpha $ и большом $k$ можно принять в качестве приближенных решений обратной задачи (31), (30). Однако на практике доступны лишь следующие сведения об уровне: данные спутниковой альтиметрии и данные наблюдений на уровнемерных постах. В работе была использована информация из DUACS DT2014 (Data Unification and Altimeter Combination System, Delayed Time mode) об аномалиях уровня и динамической топографии, полученная по данным спутниковой альтиметрии [31]. Из всего массива спутниковых данных для алгоритма вариационной ассимиляции (33)–(35) пригодны только те, которые являются измерениями на жидкой границе. Анализ данных показал, что таких измерений критически мало (1–2 за сутки). Помимо прочего, треки спутников никогда не проходят непосредственно по жидкой границе, а только лишь пересекают ее в некоторой точке. Таким образом, имеется одно-два измерения уровня за сутки в каких-то определенных точках на жидкой границе, координаты которых зависят от времени. Что касается данных наблюдений с уровнемерных постов, их получают в фиксированных точках вблизи берега (на измерительных прибрежных станциях) с определенной, заранее известной частотой.

Итерационный алгоритм (33)–(35) был реализован в качестве подключаемого модуля модели гидротермодинамики Балтийского моря. Ассимиляция данных наблюдений происходит на том шаге по времени, на котором эти данные имеются, на остальных шагах она отсутствует и расчет проходит в обычном режиме. В работе были использованы данные с уровнемерных постов Skagen (Дания), Göteborg-Torshamnen (Швеция, институт SMHI) и данные спутниковой альтиметрии DUACS DT2014. В открытом доступе [27] представлены два набора данных спутниковой альтиметрии: обработанные данные по спутниковым трекам (L3) и результат применения метода оптимальной интерполяции для построения уровня на сетке (L4) [31]. Для ассимиляции были использованы данные L3. Для получения данных в узлах сетки модели на жидкой границе в настоящей работе была использована обычная квадратичная интерполяция. Можно однозначно утверждать, что имеющихся точек с данными наблюдений слишком мало для получения сколько-нибудь близкой к реальному уровню аппроксимации. Более того, метод предполагает, что с использованием данных наблюдений на интервале $\left( {{{t}_{{{{j}_{k}}}}},{{t}_{{{{j}_{k}} + 1}}}} \right),$ где $k$ – номер шага по времени, на котором имеются данные наблюдений, решается обратная задача о восстановлении функции ${{d}_{s}},$ а дальнейший расчет при $t \in \left( {{{t}_{{{{j}_{k}} + 1}}},{{t}_{{{{j}_{{k + 1}}}}}}} \right)$ проходит с найденным (восстановленным) ${{d}_{s}}.$ В случае с редкими данными такой подход не вполне корректен, поскольку ${{d}_{s}}$ – функция, меняющаяся во времени, и предполагать ее постоянной на большие промежутки времени неправильно. Более того, следует учитывать, что функция ${{d}_{s}}$ восстанавливается не идеально, а с ошибками. Таким образом, целесообразно занулять ${{d}_{s}}$ на тех промежутках по времени, где данные отсутствуют. Однако, это тоже не верно, поскольку с физической точки зрения не описывает жидкую границу. В настоящей работе несколько шагов по времени после ассимиляции используется граничное условие из (31) с найденным ${{d}_{s}}$, затем расчет проводится с тем граничным условием, которое использовалось в модели до включения блока ассимиляции.

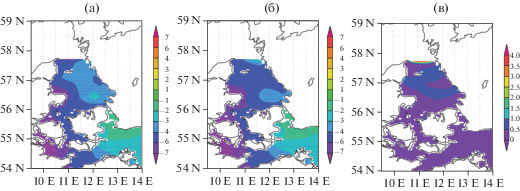
Итак, рассмотрим результаты численных экспериментов. Был проведен расчет на 14 дней с 01.03.2017 по 14.03.2017. По данным со спутников имелось всего 18 временных интервалов с измерениями уровня моря вблизи жидкой границы за весь период расчета, таким образом, ассимиляция проводилась 18 раз. На рис. 5 для сравнения представлены средние за весь период расчета уровни моря, полученные по модели с использованием ассимиляции и без нее, а также разница между ними. Как видно из рисунков, включение блока ассимиляции повлияло на средний результат вблизи жидкой границы, но практически не изменило его дальше островов.

К преимуществам алгоритма (33)–(35) относится быстрая сходимость – за 8–15 итераций достигается приемлемая точность, за 70 итераций невязка падает до минимально возможного значения. Однако из-за грубой интерполяции данных наблюдений такой точности в рассматриваемых задачах не требуется, поэтому в численных экспериментах количество итераций ограничивалось числом 8. Как показали эксперименты, итерационный метод на первых 8–15 итерациях сходится со скоростью геометрической прогрессии, что соответствует теории [24].

Заметим, что метод допускает введение различных весовых коэффициентов в функционал, учитывающих значимость тех или иных данных наблюдений. За счет таких коэффициентов можно снизить негативное влияние грубой интерполяции на результат. Также заметим, что вопрос эффективности использования предложенного в данном разделе алгоритма с реальными данными наблюдений требует дальнейшего исследования. Тем не менее, в качестве данных наблюдений для алгоритма можно также использовать данные расчета по моделям больших акваторий, как это было сделано в предыдущем разделе, однако, эффективность использования алгоритма в таком качестве ещё не исследовалась (в этом случае необходимо проводить сравнение алгоритма с известными методами вложенных сеток). Отметим, что повышение качества моделирования и прогноза морских течений наряду с ассимиляцией данных наблюдений зависит от параметризации подсеточных процессов. Особенное внимание при этом следует уделять параметризации процессов турбулентного обмена [32].

Работа выполнена при поддержке РФФИ (грант 19-01-00595, в рамках которого проведено исследование сформулированных задач), а также при финансовой поддержке Минобрнауки России (соглашение № 075-15-2019-1624).