Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 3, стр. 267-279

ВВЕДЕНИЕ

Исследование природы изменчивости в атмосфере средних широт является весьма популярной научной тематикой, начиная с 40-х гг. ХХ в. Наиболее известные математические подходы, используемые для анализа проблемы, включают построение редуцированных моделей атмосферной циркуляции, описывающих с разной степенью точности атмосферную циркуляцию на внутрисезонных временных масштабах (баротропные модели атмосферной циркуляции, двух- и трехслойные квазигеострофические модели, примитивные уравнения). С помощью линеаризации данных уравнений относительно среднего состояния атмосферы (модельного или реально наблюдаемого) удается связать собственные векторы линеаризованного оператора с ведущими модами изменчивости (т.н. естественными ортогональными функциями или ЕОФ) полей атмосферных характеристик (функции тока, приземного давления, геопотенциала или скорости) [1–6]. Другой подход основан на эмпирическом подходе и сводится к использованию данных наблюдений для реконструкции линейного оператора эволюции, порождающего наблюдаемую динамику атмосферы с последующим анализом структуры его собственных векторов [7–11]. Для более низкочастотных компонент циркуляции (на масштабах от недели до месяца) популярным подходом является построение т.н. режимов циркуляции – состояний атмосферы (например “зональный” режим и режим “блокирования”), вероятность нахождения системы в окрестностях которых максимальна [12–15]. Динамика системы в этом случае представляет собой переходы между состояниями. Данный подход тесно связан с аппроксимацией динамики атмосферы с помощью малокомпонентных марковских сетей [16–20].

Все перечисленные методы имеют свои достоинства и недостатки, оставляя место для дальнейших исследований. В настоящей работе мы рассмотрим еще один, альтернативный подход, являющийся, в каком-то смысле обобщением “теории режимов циркуляции” – вместо стационарных (квазистационарных) состояний атмосферы для аппроксимации ее динамики используются более общие множества – периодические траектории. В математической основе метода лежит утверждение теории динамических систем (доказанное для т.н. гиперболических динамических систем) о том, что любая траектория системы (и любая ее статистическая характеристика) может быть аппроксимирована с помощью периодических решений системы – траекторий системы специального вида, возвращающихся в исходное начальное состояние за конечное время (период орбиты) [21–24]. При этом статистические характеристики системы вычисляются с помощью взвешенных осреднений по соответствующим характеристикам орбит, а весовые коэффициенты определяются через характеристики неустойчивости орбит, используемых при осреднении [24]. В результате использования данного подхода можно с хорошей точностью аппроксимировать как отдельные статистические характеристики (среднее состояние, дисперсию, моды изменчивости), так и саму инвариантную меру рассматриваемой системы, связанную с понятием климата [25]. В случае моделей динамики атмосферы доказательного обоснования метода не существует, однако в ряде работ (например, [26]) высказывается предположение, что при вычислении макроскопических характеристик хаотической системы с большим числом степеней свободы ее можно считать гиперболической (т.н. “хаотическая гипотеза”). Применительно к моделям динамики атмосферы задача поиска периодических траекторий нетривиальна, поскольку сводится к решению сильно нелинейной системы дифференциальных уравнений высокой размерности (равной размерности фазового пространства системы) с плохим начальным условием. Вопрос существования периодических решений в фазовом пространстве атмосферных моделей, наличие связей между характерными режимами циркуляции и периодическими орбитами, возможность аппроксимации циркуляции с помощью периодических движений проводилось на примере моделей баротропной динамики атмосферы (океана) в работах [27–32]. В настоящей работе мы рассмотрим возможность использования периодических траекторий для аппроксимации статистических характеристик моделей динамик атмосферы более подробно, рассмотрев также квазигеострофическию модель атмосферы (т.н. модель Маршалла–Молтени [33]) и привлекая для анализа более полный набор орбит. В частности, будут сделаны выводы о структуре ведущих мод изменчивости и их связи с регулярными периодическими движениями.

Работа построена следующим образом. Во второй главе формулируются рассматриваемые модели, анализируются их статистические характеристики в сравнении с данными наблюдений. В третьей главе рассматривается методика построения периодических траекторий, и приводятся результаты по аппроксимации статистик моделей с помощью периодических орбит. В четвертой главе рассмотрены особенности циркуляции в плоскости ведущих собственных мод моделей. В заключении обсуждаются результаты работы.

МОДЕЛИ ДИНАМИКИ АТМОСФЕРЫ

Баротропная модель атмосферы основана на двумерном уравнении Навье–Стокса в сферической геометрии в терминах функции тока $\psi $ (в приближении антисимметрии относительно экватора) с учетом эффектов вращения и трения о подстилающую поверхность.

Здесь: $\psi $ – безразмерная функция тока, параметр Кориолиса обозначен $l,$ орография и ее нормировка – $h$ и $k$ соответственно, внешнее воздействие – ${{f}_{{{\text{ext}}}}},$ коэффициенты турбулентной вязкости и трения в пограничном слое обозначены $\mu $ и $\alpha $ соответственно, оператор Лапласа на сфере обозначен символом $\Delta ,$ оператор Якоби – символом $J.$

Уравнение решается с помощью метода Галеркина (базисные функции – антисимметричные относительно экватора сферические гармоники) по пространству. Используются два пространственных разрешения – T12 и T21, приводящие к системе обыкновенных дифференциальных уравнений размерности 78 и 231. Для аппроксимации по времени используется схема “midpoint” (X и τ – правая часть системы и шаг по времени):

Параметры модели были заданы следующим образом. Орография была получена из реальных данных высоты поверхности Земли в Северном полушарии (антисимметрично продолженных в Южное полушарие) с помощью разложения в ряд Фурье по базисным функциям метода Галеркина. Нормирующий множитель $k$ равен 0.14. Характерное время, соответствующее коэффициентам пограничного трения и турбулентной вязкости (для наиболее высокочастотной гармоники) составляет 25 и 5 дней соответственно. Внешнее воздействие было выбрано таким образом, чтобы среднее состояние системы было близко к среднему состоянию реальной атмосферы в январе-феврале для поля функции рассчитанной по данным реанализа NCEP/NCAR.

Методика выбора внешнего воздействия заключается в подстановке траектории реальной системы (в нашем случае данных NCEP/NCAR) в уравнение модели и вычислении остаточного слагаемого, которое после осреднения по времени и дает искомое внешнее воздействие ${{f}_{{{\text{ext}}}}}{\text{:}}$

Здесь ${{\psi }_{c}}$ функция тока из массива данных NCEP/NCAR (для 250 или 300 миллибаровой поверхности для модели грубого (T12) и “высокого” (T21) пространственных разрешений), ${{P}_{N}}$ – оператор проектирования на фазовое пространство системы. Более подробное описание данной процедуры можно найти в работах [34, 35]. При построении модели использовались данные архива для декабрей–январей–февралей 1979–2009 гг.

Линеаризация уравнения относительно среднего состояния $\bar {\psi }$ имеет следующий вид

Квазигеострофическая бароклинная модель атмосферы [33] включает три уравнения для эволюции потенциальной завихренности ${{q}_{j}}$ (в приближении антисимметрии относительно экватора) на уровнях 200, 500 и 800 мб (индексы 1, 2 и 3 соответственно). При этом учитываются эффекты вращения, взаимодействия между уровнями и трения о подстилающую поверхность.

Выражения для потенциальной завихренности имеют следующий вид:

Здесь ${{R}_{1}}~$и ${{R}_{2}}$ – радиусы деформации Россби для соответствующих уровней (равные 700 км и 450 км соответственно), $\psi $- функция тока, $l$ – параметр Кориолиса, $H$ и ${{H}_{0}}$ – орография и ее максимальное значение. Диссипационные слагаемые ${{D}_{j}}$ определяются выражениями

${{\tau }_{R}}$ обозначает время релаксации вертикального температурного профиля (равное 30 суткам); $~{{\tau }_{H}}$   – временнóй масштаб гипердиффузии (1.33 суток); R – радиус Земли; ${{\lambda }_{{{\text{max}}}}}~$ – абсолютное значение наибольшего собственного числа оператора Лапласа в модели (для разрешения Т18 оно равно λ_max = 18 × 19). Далее, $E{{K}_{3}} = \nabla \left( {{{k}_{{surf}}}\nabla {{\psi }_{3}}} \right)$ – оператор, описывающий трение о поверхность; ${{k}_{{surf}}}$ = ${{\left( {1 + 0.5LS + 0.5FH\left( h \right)} \right)} \mathord{\left/ {\vphantom {{\left( {1 + 0.5LS + 0.5FH\left( h \right)} \right)} {{{\tau }_{E}}}}} \right. \kern-0em} {{{\tau }_{E}}}},$ где LS это доля поверхности Земли в ячейке сетки, $FH\left( h \right)$ = = $1 - {\text{exp}}\left( {{{ - h} \mathord{\left/ {\vphantom {{ - h} {1000m}}} \right. \kern-0em} {1000m}}} \right),$ ${{\tau }_{E}}$ – временнóй масштаб экмановского трения, выбранный равным 1.5 суток. ${{q}_{i}}' = {{q}_{i}} - f,$ $~i = 1,2,$ и ${{q}_{3}}' = {{q}_{3}} - f\left( {{{1 + h} \mathord{\left/ {\vphantom {{1 + h} {{{H}_{0}}}}} \right. \kern-0em} {{{H}_{0}}}}} \right).$

Процедура выбора правой части аналогична процедуре, используемой для баротропной модели. Для каждого из уравнений ${{F}_{j}}$ определяется подстановкой данных функции тока на поверхностях 200, 500, 800 мб из архива реанализа NCEP/NCAR и соответствующим осреднением:

На рис. 1 представлены статистические характеристики рассматриваемых моделей в сравнении с данными наблюдений. Первая строка – средние состояния баротропной модели низкого разрешения, баротропной модели Т21, модели Маршала–Молтени (уровень 1, соответствующий 200 мб) и функции тока на поверхности 250 мб по данным архива NCEP/NCAR. Во второй строке – поля среднеквадратических отклонений (в данных NCEP/NCAR предварительно отфильтровывались частоты короче трех и длиннее 90 сут).

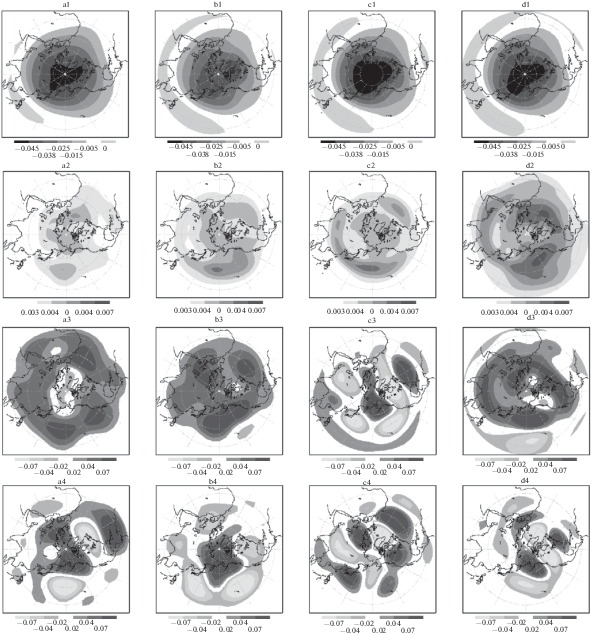
Отметим, что при построении внешних воздействий для модели T12 использовались данные функции тока 250 мб (для T21 – 300 мб), именно поэтому ее среднее состояние наиболее близко к наблюдениям. Кроме того видно, что все модели занижают дисперсию поля функции тока, при этом бароклинная модель является наиболее реалистичной. В третьей и четвертой строчках рис. 1 показаны первая и вторая ведущие естественные ортогональные функции (ЕОФ) моделей и данных. При построении ЕОФ для данных снова проводится фильтрация с окном 3–90 дней. Видно, что первая ЕОФ данных, идентифицируемая как круговая мода, хорошо воспроизводится баротропными моделями. Вторая ЕОФ поля наблюдений, имеющая структуру, сходную с PNA близка к первой ЕОФ бароклинной модели и имеет некоторое сходство со вторыми ЕОФ баротропных моделей. Вторая ЕОФ бароклинной модели идентифицируется как “волна три”, также выделяющаяся при анализе данных наблюдений. Отсутствие круговой моды в ведущих ЕОФ1 и ЕОФ2 бароклинной модели связано с тем, что ее данные не фильтруются и содержат значительную долю короткопериодной бароклинной изменчивости (это необходимо для унификации анализа моделей в следующих главах).

Рассмотрим далее структуру линейных мод циркуляции на уровне 250 мб. Как показано в работе [36], линеаризация баротропного уравнения вихря относительно среднего состояния атмосферы на этом уровне дает наибольшие значения корреляции ведущих собственных векторов с ведущими модами изменчивости. Линейный оператор (2) имеет 6 пар неустойчивых комплексных собственных векторов, периоды которых равны 12, 8, 5, 3, 90 и 30 дням. На рис. 2 в первой строке (a1–c1) показаны мнимые части векторов, отвечающих периодам 8, 12 и 30 (собственные векторы 2, 1 и 6). Второй и первый векторы (a1 и a2) имеют структуру волн “шесть” и “пять”, распространяющихся с запада на восток, в структуре шестого вектора (a3) присутствует структура типа PNA и (на севере) волна “один”. Заметим, что линеаризация уравнения (2) относительно среднего состояния реальной атмосферы (вычисленного по архиву NCEP/NCAR) дает аналогичные результаты (выделяются все перечисленные выше моды) с той лишь разницей, что среди ведущих векторов появляются и более высокочастотные моды с характерными периодами двое и трое суток и волновыми числами 7 и 8.

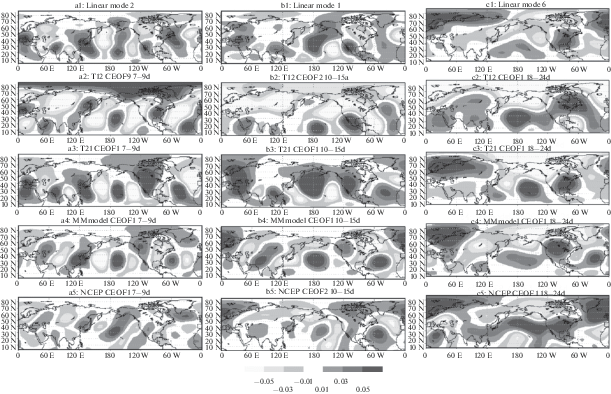
Регулярные колебательные процессы лучше всего выделяются с помощью построения комплексных ЕОФ. Процедура вычисления гильбертовых ЭОФ для траектории системы заключается в следующем (см. [37]). Сначала производится преобразование Фурье по времени для каждой компоненты рассматриваемого физического поля. Далее, в полученном разложении производится его сдвиг на четверть периода (90 град.) и обратное преобразование Фурье. В результате получаем исходный временной ряд $\psi \left( j \right)$ и его гильберт-преобразование$~\tilde {\psi }\left( j \right).$ Далее необходимо составить комплексную переменную $z\left( j \right) = \psi \left( j \right) + i\tilde {\psi }\left( j \right)$ и вычислить для нее ковариационную матрицу. Комплекснозначные собственные векторы этой матрицы есть гильбертовы (или комплексные) ЭОФ системы, определяющие двумерные плоскости с наибольшей изменчивостью решения. На рис. 2 показан результат комплексного ЕОФ-анализа данных баротропных и бароклинной моделей, к которым применена фильтрация с окном 7–9, 10–15 и 18–30 дней (приводится лишь одна компонента комплексной ЕОФ, имеющая наибольшую корреляцию с соответствующей линейной модой). Баротропная модель низкого разрешения (вторая строка, a2–c2) плохо разрешает высокочастотные моды, поэтому линейная мода 2 реализуется лишь в виде 9-ой по счету ЕОФ (рис. 2a2), а первая мода – в виде второй ЕОФ. 30‑дневная структура 6-ой моды выделяется в первой ЕОФ. Структура изменчивости баротропной модели высокого разрешения близка к ее собственным модам, все моды выделяются в виде ведущих комплексных ЕОФ (рис. 2а3–с3). Изменчивость функции тока верхнего уровня модели Маршала–Молтени (рис. 2а4–с4) также близка к собственным модам баротропной циркуляции, представленным в виде ведущих ЕОФ с близкой структурой. Реальные данные имеют гораздо более богатую структуру изменчивости, однако собственные моды баротропной динамики здесь также выделяются (рис. 2а5–с5). Волна “шесть” реализуется в виде ведущей комплексной ЕОФ, волна “пять” в виде второй ЕОФ, а структура “волна один”-PNA – в виде третьей ЕОФ.

ПЕРИОДИЧЕСКИЕ ОРБИТЫ СИСТЕМЫ И ЕЕ СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ

По определению, периодической орбитой является специальная траектория системы, которая через фиксированное время T (период орбиты) возвращается в свое исходное положение. В символьном виде это можно записать как

где $S\left( {T,\psi \left( 0 \right)} \right)$ это нелинейный оператор эволюции, определяющий состояние системы с начальным состоянием в точке $\psi \left( 0 \right)$ через время $T.$ Соотношение, определяющее орбиту, является, по сути, нелинейной системой из $N$ уравнений для $N + 1$ неизвестного, поскольку $\psi \left( T \right)~$нелинейно зависит и однозначно определяется $\psi \left( 0 \right)$ и $T.$ Недоопределенность системы вызвана тем, что одна и та же орбита может быть задана различными начальными условиями, которые получаются друг из друга сдвигом вдоль периодической траектории. Для решения системы уравнений могут быть использованы различные численные методы. В данной работе мы использовали метод Ньютона с подавлением шага (см., например, [38]), при этом необходимо доопределить систему, устранив свободу выбора начального условия. Это можно сделать, добавив к системе уравнений фазовое условие, смысл которого заключается в том, что направление поиска выбирается ортогональным к направлению движения.

Кратко проиллюстрируем численную схему метода (детали можно найти в [29]). Пусть ${{\psi }^{{\left( k \right)}}}$ и ${{T}^{{\left( k \right)}}}$ являются (k)-ми приближениями для $\psi \left( 0 \right)$ и $T.$ Обозначим ${{\psi }^{{\left( {k + 1} \right)}}} = {{\psi }^{{\left( k \right)}}} + {{h}^{{\left( k \right)}}}$ и ${{T}^{{\left( {k + 1} \right)}}} = {{T}^{{\left( k \right)}}} + {{\tau }^{{\left( k \right)}}}.$ Стандартная итерация метода Ньютона основана на разложении уравнения

в ряд Тейлора по ${{h}^{{\left( k \right)}}}~$ и ${{\tau }^{{\left( k \right)}}}~$ с точностью до малых первого порядка. В результате получается линейная система уравнений для ${{h}^{{\left( k \right)}}}~$ и ${{\tau }^{{\left( k \right)}}}.$ А именно,

Потребуем ортогональность направления поиска ${{h}^{{\left( k \right)}}}$ направлению движения (правой части системы) в текущем начальном состоянии:

Система линейных уравнений в невырожденном случае однозначно определяет ${{h}^{{\left( k \right)}}}~$и ${{\tau }^{{\left( k \right)}}},$ при этом следующее приближение вычисляется как

Параметр $\eta $ равен единице в стандартном методе Ньютона. Однако если линейная система плохо обусловлена, шаг $\left( {{{h}^{{\left( k \right)}}},{{\tau }^{{\left( k \right)}}}} \right)$ может быть большим. В этом случае разложение в ряд Тейлора с точностью до слагаемых первого порядка не имеет смысла, и метод Ньютона может расходиться. Как показывают результаты расчетов, для рассматриваемой задачи подавление шага является обязательной процедурой. Для выбора величины $~~\eta $ в работе была использована методика “line search”, описанной в [38]. Заметим, что каждая итерация метода Ньютона требует интегрирования линеаризованной модели в полном фазовом пространстве.

Для определения среднего значения какой-либо статистической характеристики системы ${\Psi }\left( \psi \right)$ модель интегрируется в течении длительного времени, ${\Psi \;}$ оценивается в каждой точке полученной траектории и усредняется по всем моментам времени

при этом, все измерения $\psi \left( k \right)$ учитываются с одинаковым весом, равным единице.

Согласно теории гиперболических систем (см. [24]), зная набор всех периодических траекторий системы с периодом меньшим $T,$ среднее $\left\langle {\Psi } \right\rangle $ можно определить, вычисляя ${\Psi }$ в точках, лежащих на периодических траекториях:

где ${{\psi }_{i}}$ – периодическая точка периода ${{t}_{i}} < T,$ $I\left( T \right)$ – общее число таких точек, каждая орбита периода ${{t}_{i}}$ содержит ${{{{t}_{i}}} \mathord{\left/ {\vphantom {{{{t}_{i}}} \tau }} \right. \kern-0em} \tau }$ периодических точек ($\tau $ – шаг по времени в модели), ${{w}_{i}}$ – вес орбиты (одинаковый для всех ее периодических точек), $W$ – суммарный вес всех периодических точек. Вес орбиты ${{w}_{i}}$ определяется как где $\lambda \left( {i,m} \right)$ – положительные ляпуновские показатели орбиты, соответствующей i-ой периодической точке. Таким образом, формула имеет такой же смысл, что и стандартное определение среднего, только значение функционала для конкретной периодической точки учитывается не с одинаковым единичным весом, а с весом, пропорциональным характеристикам неустойчивости орбиты – скорости роста фазового объема вдоль ее неустойчивых направлений. Чем выше скорость роста, тем меньше вес. Слабо неустойчивые орбиты вносят определяющий вклад при вычислении среднего, что физически оправдано, поскольку траектория проводит больше времени в окрестности таких орбит.

С помощью указанных методик для каждой из моделей был найден набор орбит, который будет использован для вычисления статистических характеристик моделей наряду со стандартным определением. Для баротропной модели T12 было найдено 2322 орбиты, для ее версии разрешения T21 – 1851 орбита, для модели Маршала–Молтени – 2711 орбит. Заметим, что справедливость аппроксимации гарантируется теоремно, если изучаемая система является гиперболической и если найдены все орбиты вплоть до достаточно большого периода. Гарантировать эти факты мы, разумеется, не можем. Более того, число орбит, необходимое для корректной реконструкции траектории системы экспоненциально зависит от ее сложности, поэтому можно ожидать, что для модели Маршала–Молтени, имеющей наибольшую размерность аттрактора и наибольшую скорость нарастания ошибки, тестируемый подход даст наихудшие результаты.

Результат аппроксимации базовых статистических характеристик рассматриваемых моделей с рис. 1 (среднее состояния, изменчивость, первый и второй ведущие ЕОФ) с помощью периодических траекторий и использования представлений (10–11), представлен на рис. 3. Видно, что характеристики наиболее простой баротропной модели T12 воспроизводятся точно, в случае модели Т21 занижается дисперсия, второй ЕОФ воспроизводится хуже. Для наиболее сложной модели Маршала–Молтени изменчивость еще более занижена, ведущие ЕОФ, имеющие характерный временной масштаб порядка 20-ти дней воспроизводятся плохо. Данный факт объясняется тем, что для модели Маршала–Молтени число найденных орбит с периодами более 10-ти дней мало, и при вычислении ЕОФ доминируют высокочастотные моды.

СТРУКТУРА ЦИРКУЛЯЦИИ В ПЛОСКОСТИ ВЕДУЩИХ ЕОФ

Рассмотрим далее, каким образом устроена циркуляция в плоскости собственных мод баротропной циркуляции. Для этого спроектируем траекторию каждой модели на соответствующую двумерную плоскость комплексной ЕОФ с рис. 2. Таким образом, для каждой точки траектории мы получим двухкомпонентный вектор (${{x}_{1}}\left( i \right),$ ${{x}_{2}}\left( i \right)$) ≡ ≡ $r\left( i \right).$ Скорость движения на плоскости будет равна (${{x}_{1}}\left( {i + 1} \right) - {{x}_{1}}\left( i \right),$ ${{\left. {{{x}_{2}}\left( {i + 1} \right) - {{x}_{2}}\left( i \right)} \right)} \mathord{\left/ {\vphantom {{\left. {{{x}_{2}}\left( {i + 1} \right) - {{x}_{2}}\left( i \right)} \right)} \tau }} \right. \kern-0em} \tau } \equiv u\left( i \right).$ Угол вращения $\theta $ в двумерной плоскости за 1 шаг по времени равен (если среднее вычтено) $\theta = {\text{arcsin}}\left[ {r\left( {i + 1} \right) \times {{r\left( i \right)} \mathord{\left/ {\vphantom {{r\left( i \right)} {\left| {r\left( {i + 1} \right)} \right|}}} \right. \kern-0em} {\left| {r\left( {i + 1} \right)} \right|}}\left| {r\left( i \right)} \right|} \right]$ и соответствующий период вращения можно вычислить как ${{T}_{{\theta }}} = {{2\pi \tau } \mathord{\left/ {\vphantom {{2\pi \tau } \theta }} \right. \kern-0em} \theta }.$ Построим далее боксовым методом плотность вероятности для проекции решения на выбранную плоскость и плотность вероятности для тех точек, скорость которых вдоль данной плоскости $u\left( i \right)$ по норме составляет как минимум 50% от полной скорости решения ${{\left( {\psi \left( {i + 1} \right) - \psi \left( i \right)} \right)} \mathord{\left/ {\vphantom {{\left( {\psi \left( {i + 1} \right) - \psi \left( i \right)} \right)} \tau }} \right. \kern-0em} \tau }$ (т.е. движение в данный момент времени происходит в основном вдоль данной плоскости).

На рис. 4a1–a3 представлены плотности вероятности проекций решения баротропной модели Т21 на плоскости комплексных ЕОФ с рис. 2 (a3, b3 и c3), на рис. 4b1–b3 – проекции решения на те же плоскости, но для состояний скорость которых вдоль данной плоскости по норме превосходит 0.5 от полной нормы скорости. Время обращения ${{T}_{\theta }}$ для соответствующих плоскостей показано на рис. 4с1–с3. Можно сказать, что для всех проекций распределения имеют квазигауссову форму с единственным максимумом. В этом смысле, режимы циркуляции не выделяются. В то же время, если рассматриваются состояния, эволюция которых в значительной степени определяется процессом, определяющим соответствующий комплексный ЕОФ (например, распространение волны Россби с волновым числом 6, как на рис. 4a1), то плотность вероятности имеет нетривиальный характер, приобретая форму “бублика”. Траектории системы описывают регулярные вращения в фазовом пространстве вокруг начала координат.

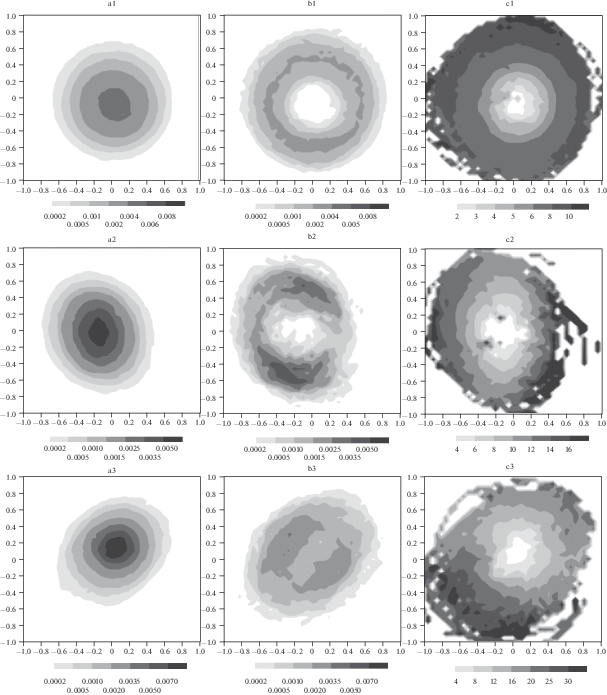
Период вращения близок к характерному периоду собственной моды линейного оператора баротропной задачи (6–8 дней (рис. 4с1) для плоскости рис. 2a3, и 10–14 дней (рис. 4с2) для плоскости рис. 2b3). При увеличении окна фильтрации до 18–24, т.е. при рассмотрении более низкочастотных колебаний, характер циркуляции становится более сложным, регулярные движения вокруг среднего состояния перестают доминировать, в распределении периодов вращательного движения появляется асимметрия.

Похожая картина имеет место и для периодических орбит системы (рис. 5). Для короткопериодных мод изменчивости правильно выделяются особенности структуры плотности вероятности и характерные времена. Это означает, что траектории модели действительно совершает регулярные вращательные движения вокруг начала координат вдоль кластера соответствующих периодических траекторий. Для низкочастотных колебаний качество аппроксимации ухудшается, главным образом из за того, что количество орбит с периодом, большим 10 дней, полученное с помощью численного алгоритма недостаточно для корректного описания динамики.

Для баротропной модели Т12 наблюдается похожая картина – имеют место регулярные колебательные движения для 10–15 дневных мод и сложная низкочастотная динамика, колебания с характерным временем 7–9 дней в модели отсутствуют. Орбиты аппроксимируют все детали динамики с большей точностью, чем для модели Т21. Модель Маршала–Молтени демонстрирует аналогичную динамику, однако, ее аппроксимация периодическими движениями возможна только для наиболее высокочастотных мод (7–9 дней и короче).

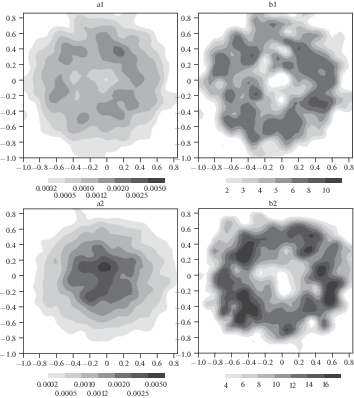
Аналогичный анализ данных реальной климатической системы показывает, что и реальная циркуляция атмосферы имеет похожую структуру. Используя весь имеющийся архив NCEP/NCAR (1948–2015 гг., ноябрь–март) для функции тока поверхности 250 мб были построены комплексные ЕОФ для фильтрованных данных с окнами фильтрации 4–6 и 10–15 сут. Были вычислены состояния, для которых норма проекции скорости на выбранную плоскость превышает 0.45 от нормы скорости. Далее для этих состояний были построены двумерные плотности вероятности (рис. 6a1 – для CEOF1 и фильтра 4–6 дней, рис. 6a2 – для CEOF1 и фильтра 10–15дней) и оценено характерное время обращения вокруг среднего состояния (рис. 6b1 и рис. 6b2 соответственно).

ЗАКЛЮЧЕНИЕ

В работе рассматривается связь между собственными модами (собственными векторами линеаризованных относительного среднего состояния) моделей динамики атмосферы, ведущими модами изменчивости модельной циркуляции и неустойчивыми периодическими решениями уравнений моделей (решениями, возвращающимися в исходное состояние через заданное время).

Для поиска периодических траекторий реализован эффективный вычислительный алгоритм. Показано, что в фазовых пространствах моделей существует набор периодических решений, достаточный для аппроксимации базовых статистических характеристик моделей (среднего состояния, дисперсии, ведущих мод изменчивости). При этом, для наиболее сложной из рассматриваемых моделей (модели Маршала–Молтени) моды низкочастотной изменчивости (с периодами более двух недель) аппроксимируются недостаточно хорошо, что, по-видимому, связано с недостаточным количеством найденных орбит.

Кластеры орбит можно связать с различными колебательными процессами в фазовом пространстве рассмотренных атмосферных моделей – волнами Россби различного пространственного масштаба, осцилляционными структурами типа PNA и NAO. Для высокочастотных мод изменчивости динамика системы реализуется в виде регулярного периодического движения в плоскостях комплексных естественных ортогональных функций, при этом траектория системы повторяет круговое движение орбит с тем же периодом. Плотность вероятности точек, совершающих такие вращения, имеет вид тора, который хорошо аппроксимируется при помощи периодических орбит. Как правило, плоскость регулярного движения совпадает с плоскостью наиболее неустойчивых собственных мод баротропной динамики. Интересен тот факт, что линейный характер динамики наблюдается не рядом со средним состоянием, а на некотором расстоянии от него. Это может быть интерпретировано в рамках линейного динамико-стохастического подхода к описанию атмосферной циркуляции, когда динамический оператор аппроксимируется устойчивым линейным оператором и стохастическим нелинейным слагаемым, моделирующим нелинейные взаимодействия системе. Когда состояние системы далеко от среднего, доминирует линейная часть тенденции, и наоборот для состояний близких к среднему.

В случае более низкочастотных процессов (от 14 дней и более) динамика имеет более сложный характер, не описываемый простыми двумерными вращениями. Наряду с линейными процессами (например, волна “один”, распространяющаяся с востока на запад) присутствуют и более сложные моды с нелинейной динамикой (круговая мода, NAO). При этом, возможность аппроксимации динамики периодическими траекториями все равно сохраняется. Анализ данных наблюдений показывает, что, по-видимому, такие же выводы можно сделать и для реальной атмосферной циркуляции. Проекции решения на высокочастотные моды изменчивости предполагает наличие периодических (квазипериодических) траекторий у реальной атмосферы.

Благодарности. Работа выполнена при государственной поддержке научного центра мирового уровня “Московский центр фундаментальной и прикладной математики” (разработка методов поиска периодических траекторий) и гранта РФФИ 17-55-10012 KO_a (анализ моделей).