1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 56, № 5, 2020

Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 5, стр. 567-574

Сравнение дисперсионной и бездисперсионной моделей наката длинных волн на берег

А. Абдалазиз a, И. И. Диденкулова a, b, c, *, Д. Дутых d, П. Денисенко e

a Отделение морских систем, Таллинский технологический университет
12618 Таллинн, Акадеемиа тее, 15А, Эстония

b Нижегородский государственный технический университет им. Р.Е. АлексееваГСП-41, ул. Минина, 24
603950 Нижний Новгород, Россия

c Институт прикладной физики РАН
603950 Нижний Новгород, ул. Ульянова, 46, Россия

d Университет Гренобль Альпы, Университет Савойя Мон Блан, Национальный центр научных исследований, Лаборатория математики
73000 Шамбери, Франция

e Университет Уорика
CV4 7AL Ковентри, Великобритания

* E-mail: dii@appl.sci-nnov.ru

Поступила в редакцию 28.06.2019
После доработки 27.03.2020
Принята к публикации 01.04.2020

Полный текст (PDF)

Аннотация

В данной работе мы исследуем применимость дисперсионной и бездисперсионной модели для описания распространения и наката длинных волн на берег в случае составного рельефа дна: плоский откос переходит в зону постоянной глубины. Численные расчеты проводятся в рамках двух моделей: (1) нелинейная теория мелкой воды и (2) дисперсионная модель в приближении Буссинеска, основанная на модифицированных уравнениях Перегрина, и сравниваются с данными лабораторного эксперимента для различных типов волн: регулярные, бигармонические и “судовые” пакеты волн, сильно модулированные по частоте и амплитуде. На основе проведенного сравнения делаются выводы о применимости соответствующих теорий для описания данных типов волн.

Ключевые слова: волны на воде, накат длинных волн на берег, частотная дисперсия, нелинейная теория мелкой воды, дисперсионная теория, модифицированные уравнения Перегрина

1. ВВЕДЕНИЕ

В современной литературе для описания наката длинных волн на берег чаще используется нелинейная теория мелкой воды, чем дисперсионные модели, в частности, уравнения типа Буссинеска. Для объяснения этого существует несколько причин. Во-первых, при приближении к берегу дисперсионный член в уравнениях Буссинеска становится незначительным по сравнению с нелинейным членом [1]. Во-вторых, расчеты наката волн, проведенные с помощью дисперсионных кодов, менее устойчивы по сравнению с расчетами, проведенными в рамках нелинейной теории мелкой воды [2]. В-третьих, нелинейная теория мелкой воды считается более адекватной моделью в задачах оценки риска цунами, поскольку она имеет низкое расчетное время и ей не свойственна недооценка высоты наката [3]. По этой же причине нелинейная теория мелкой воды предпочтительнее для оперативного прогноза цунами [4].

Отметим также, что для цунами зачастую первая (лидирующая) волна достаточно хорошо описывается обеими моделями, в то время как дисперсионные эффекты важны для описания последующих волн [5]. Тут следует сказать, что первая волна цунами далеко не всегда наибольшая, что часто наблюдается во время транс-океанических цунами, распространяющихся на большие расстояния [6]. Также дисперсионные эффекты могут проявляться и в “задержке” времени распространения волн цунами [7].

Большинство приведенных выше исследований основывались только на численных расчетах и не имели опорных измерений для контроля результатов самих моделей. В данной работе мы сравниваем высоты наката волн на берег, рассчитанные с помощью двух моделей, с экспериментальными данными наката различных типов волн: одиночные волны, регулярные и бигармонические волны, а также частотно модулированные волновые пакеты. В качестве моделей используются нелинейная теория мелкой воды и модель типа Буссинеска, основанная на модифицированных уравнениях Перегрина.

2. ДАННЫЕ ЛАБОРАТОРНОГО ЭКСПЕРИМЕНТА

Лабораторный эксперимент проводился в Большом волновом канале (Großer Wellenkanal) Ганновера, в Германии в 2012–2013 гг. [8, 9]. В эксперименте использовалась стандартная геометрия канала, который состоит из участка ровного дна длиной 251 м, заканчивающегося плоским откосом с тангенсом берегового уклона 1 : 6 (рис. 1). Во время экспериментов глубина воды поддерживалась постоянной и была равна 3.5 м. Измерения вдоль длины канала проводились с помощью 18 струнных волнографов. Колебания наката измерялись емкостным датчиком, а также двумя видеокамерами с высоким разрешением. Ошибка измерения наката емкостным датчиком определяется вариацией уреза воды поперек склона. По визуальным наблюдениям, вариация составляет около ±3% от величины наката.

Рис. 1.

Схема лабораторного эксперимента в Большом волновом канале.

Экспериментальный лоток имел грубое асфальтовое покрытие, которое особенно сказывалось на измерении отката волн. При движении воды вниз от уреза, на склоне оставался слой воды, который касался провода емкостного датчика, что мешало корректному прописыванию отката волн.

Волны возбуждались с помощью лопастного волнопродуктора, уже ранее применявшегося для генерации длинных волн типа цунами [10]. Волнопродуктор был оборудован механизмом активного поглощения отраженной волны [11], использующим в качестве входных параметров сигналы с двух волнографов: одного в непосредственной близости и другого в 3.6 м от лопасти. Однако чтобы исключить влияние даже небольшой части волны, отраженной от волнопродуктора, для расчетов использовались только первые четыре волны, на которых отражение еще не сказалось.

Полный список исследуемых волн включал регулярные и бигармонические волны, а также модулированные по частоте и амплитуде волновые пакеты, напоминающие характерные записи волн от высокоскоростных судов [12, 13]. В таких генерируемых волновых пакетах период волн линейно уменьшался от 20 до 10 с.

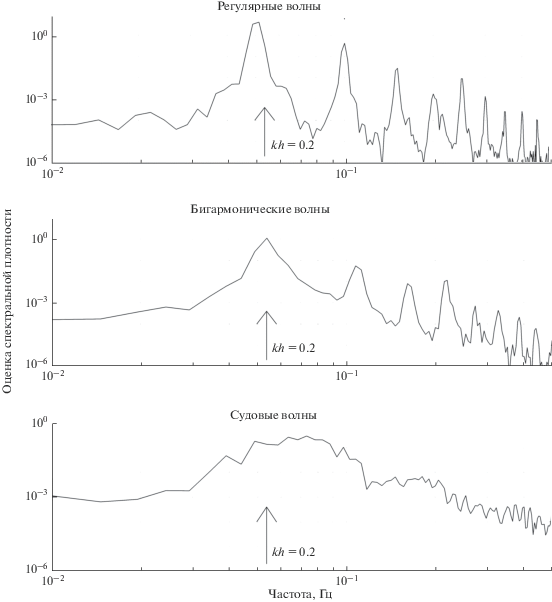
Характерные оценки спектральной плотности мощности для трех типов рассматриваемых волн представлены на рис. 2. Из рисунка видно, что для регулярных и бигармонических волн основной период одинаков и равен 20 с, в то время как для судовых волн период 20 с соответствует началу широкого пика. Длина таких волн в канале глубиной h = 3.5 м в приближении линейных гравитационных волн равна 117 м, а параметр kh = 0.2, где k – волновое число, что соответствует условиям мелкой воды.

Рис. 2.

Оценка спектральной плотности мощности исследуемых типов волн.

В качестве основного параметра для сравнения вычислений с экспериментом использовалась высота наката.

3. ЧИСЛЕННЫЕ МОДЕЛИ

В численных расчетах использовались две модели: нелинейная теория мелкой воды и дисперсионные уравнения типа Буссинеска, основанные на модифицированных уравнениях Перегрина [14]. Обе модели учитывали донное трение по формуле Маннинга [15]. Соответствующий коэффициент шероховатости был взят равным 0.016 с/м1/3, что соответствует грубому асфальтовому покрытию [16]. Влияние трения при накате длинных волн на берег рассмотрено в [17].

Используемая в численных расчетах батиметрия повторяла геометрию Большого волнового канала:

(1)
$h(x) = \left\{ {\begin{array}{*{20}{c}} {{{h}_{0}},}&{x \in \left[ {a,b} \right]} \\ {{{h}_{0}} - \left( {x - b} \right){\text{tg}}\alpha ,}&{x \in \left[ {b,c} \right]} \end{array}} \right.,$
где h0 = 3.5 м – это постоянная глубина бассейна, α – угол берегового склона (tg α = 1 : 6). За х = 0 взято положение волнопродуктора, от которого отсчитываются все расстояния. Участок [a, c] соответствует левой и правой границе численного лотка, точка b = 251 м соответствует началу берегового склона (см. рис. 1).

В качестве граничного условия слева (x = a) использовалась наиболее “чистая” экспериментальная запись волнографа в точке, наиболее приближенной к волнопродуктору. Это была запись волнографа, установленного на расстоянии a = 50 м от волнопродуктора.

Условий же на скорости течения не накладывалось. Как доказано в работе [18], постановка задачи с одним краевым условием на каждой границе в докритическом режиме (усредненная по глубине горизонтальная скорость частиц жидкости меньше скорости распространения длинных волн, т.е. число Фруда меньше единицы) корректна. Такой выбор граничных условий обеспечивает прозрачность их задания.

Число точек пространственной сетки было постоянным и равно 4000 для всех экспериментов, так что пространственное разрешение составляло 6.3 см. Для дискретизации во времени мы использовали вложенные методы Рунге–Кутты 3 и 2 порядка [19], реализованные в среде МАТЛАБ с помощью команды ode23 [20]. Таким образом, в каждом вычислении для выбора шага по времени использовалась адаптивная схема с установленным желаемым уровнем погрешности, равным 10–4. Характерный временной шаг, используемый в обеих моделях (нелинейная теория мелкой воды и модифицированные уравнения Перегрина), для различных типов экспериментов представлен в табл. 1.

Таблица 1.  

Характерный шаг по времени в проведенных расчетах; типы волн: 1 – регулярная волна, 2 – бигармоническая волна, 3 – частотно модулированный волновой пакет

Тип волн Модифицированные уравнения Перегрина, Δt, с Нелинейная теория мелкой воды, Δt, с
1 0.012 0.013
2 0.012 0.013
3 0.009 0.012

В обеих моделях реализован метод конечных объемов. Численная схема основана на локально полиномиальной реконструкции второго порядка, см. [21].

4. РАСПРОСТРАНЕНИЕ И НАКАТ ВОЛН

Две описанные выше модели (нелинейная теория мелкой воды и модифицированные уравнения Перегрина) использовались для описания эксперимента, проведенного в Большом волновом канале и описанного в разделе 2. Было проведено моделирование всех указанных выше типов волн. Численные расчеты в соответствующих точках были сопоставлены с имеющимися измерениями колебаний водной поверхности вдоль канала и на берегу. В частности, были сопоставлены рассчитанные и измеренные максимальные высоты наката первых четырех волн для каждого типа волн. Также для каждой модели и для каждого типа волн было рассчитано отклонение от экспериментально измеренного значения, нормированное на величину экспериментального наката (рис. 3). Цифрами на графике представлены максимальные накаты первой, второй, третьей и четвертой волн. Видно, что в расчетах, сделанных с помощью дисперсионной теории, разброс между расчетом и экспериментом меньше, и, в целом, дисперсионная теория более достоверно описывает экспериментальные данные. Также видно, что с увеличением амплитуды волн разница между расчетом и экспериментом уменьшается и, в конце концов, приводит к недооценке высоты наката. Этот эффект связан с обрушением волн.

Рис. 3.

Сравнение высот наката, рассчитанных с помощью нелинейной теории мелкой воды (левая колонка) и модифицированного уравнения Перегрина (правая колонка), для разных типов волн. Цифры 1, 2, 3 и 4 отвечают высоте наката первой, второй, третьей и четвертой волны.

Рассмотрим разные типы волн по-отдельности.

4.1. Регулярные волны

На рис. 4 показаны колебания водной поверхности для регулярной волны высоты 0.2 м. Видно, что как нелинейная теория мелкой воды, так и дисперсионная теория, достаточно хорошо описывают экспериментальные данные.

Рис. 4.

Колебания водной поверхности для регулярной волны высотой 0.2 м. Экспериментальная запись представлена сплошной линией, расчеты в рамках нелинейной теории мелкой воды представлены штрихпунктирной линией, а расчеты в рамках модифицированных уравнений Перегрина – штриховой линией. Горизонтальный отрезок соответствует времени прихода отраженной от волнопродуктора волны.

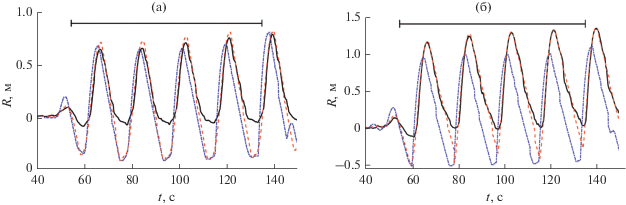
На рис. 5а показан плавный накат регулярной волны малой высоты 0.2 м, в то время как на рис. 5б мы видим накат более нелинейной волны высотой 0.4 м. Видно, что если накат слабонелинейной волны (рис. 5а) примерно одинаково описывается обеими моделями, то для описания наката более нелинейной волны (рис. 5б), дисперсионная теория является более адекватной моделью. Как уже отмечалось выше, при откате волны в эксперименте на склоне оставался слой воды, который касался провода емкостного датчика, поэтому датчик плохо прописывал нисходящие участки сигнала. Особенно ярко это выражено в записях волн большой амплитуды, нелинейные эффекты в которых наиболее сильно проявляются на стадии отката волн [22, 23].

Рис. 5.

Накат регулярных волн высотой а) 0.2 м и б) 0.4 м. Экспериментальная запись представлена сплошной линией, расчеты в рамках нелинейной теории мелкой воды представлены штрихпунктирной линией, а расчеты в рамках модифицированных уравнений Перегрина – штриховой линией. Горизонтальный отрезок соответствует времени прихода отраженной от волнопродуктора волны.

Несмотря на то, что на качественном уровне обе модели хорошо воспроизводят эксперимент, см. рис. 4 и рис. 5, есть количественная разница, которая особенно заметна для значений максимального наката (рис. 3). Из рис. 3 видно, что дисперсионная теория характеризуется меньшим отклонением от данных эксперимента и, в целом, более достоверно описывает регулярные волны. Также видно, что обе теории склонны недооценивать накат волн большой амплитуды, что является следствием обрушения волн (см. рис. 3).

4.2. Бигармонические волны

Из рис. 6 видно, что даже для бигармонических волн низкой амплитуды нисходящая ветка (откат) еще хуже прописывается экспериментом, чем в случае регулярных волн. Вероятно, это связано с наличием коротковолновой составляющей в спектре.

Рис. 6.

Накат бигармонических волн высотой а) 0.27 м и б) 0.4 м. Экспериментальная запись представлена сплошной линией, расчеты в рамках нелинейной теории мелкой воды представлены штрихпунктирной линией, а расчеты в рамках модифицированных уравнений Перегрина – штриховой линией. Горизонтальный отрезок соответствует времени прихода отраженной от волнопродуктора волны.

В рамках рассмотренных высот волн дисперсионная модель показала себя как более надежная (рис. 6). При низких амплитудах волн она слегка завышала высоту наката (4–17%), давая при этом меньший разброс, чем нелинейная теория мелкой воды, которая как завышала (до 20%), так и занижала (до 10%) значения высоты наката. При более высоких амплитудах она могла слегка занизить (не более 3%) высоту наката, обеспечивая минимальный разброс по сравнению с нелинейной теорией мелкой воды, которая занижала значения наката вплоть до 25%.

4.3. Частотно модулированные пакеты волн

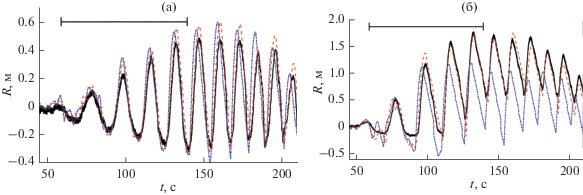
И, наконец, рассмотрим самый необычный тип волн в данной коллекции – модулированные по частоте и амплитуде волновые пакеты. Период таких волн уменьшался линейно с 20 до 10 с. Накат этих волн для экспериментальных тестов с максимальными высотами 0.12 и 0.42 м показан на рис. 7. Видно, что с описанием волн меньшей амплитуды (рис. 7а) обе модели справляются примерно одинаково, в то время как при описании волн большей амплитуды (рис. 7б), теория мелкой воды явно проигрывает, занижая ожидаемую высоту наката на более, чем 40%. Это занижение высоты наката для более высоких волн связано с эффектами обрушения волн. Дисперсионная же теория, основанная на модифицированных уравнениях Перегрина, при описании частотно модулированного волнового пакета ведет к меньшей ошибке. При этом недооценка высоты наката для самых высоких волн не превышает 7%. Как и в случае регулярных волн, описанная тенденция наблюдается для большинства волн в группе (рис. 3).

Рис. 7.

Накат волновых пакетов, модулированных по частоте и амплитуде, с максимальной высотой а) 0.12 м и б) 0.42 м. Экспериментальная запись представлена сплошной линией, расчеты в рамках нелинейной теории мелкой воды представлены штрихпунктирной линией, а расчеты в рамках модифицированных уравнений Перегрина – штриховой линией. Горизонтальный отрезок соответствует времени прихода отраженной от волнопродуктора волны.

Если провести сравнение непосредственно между предсказаниями двух численных моделей, то видно, что, как и в предыдущем случае, предсказания теории мелкой воды имеют бóльшую ошибку, чем предсказания дисперсионной теории (рис. 3). Но в данном случае ошибка предсказаний теории мелкой воды может быть как положительной (переоценка), так и отрицательной (недооценка).

5. ЗАКЛЮЧЕНИЕ

В данной работе мы сравнили возможности двух моделей: нелинейной теории мелкой воды и дисперсионной теории в приближении Буссинеска, представленной модифицированными уравнениями Перегрина, для описания распространения и наката длинных волн на берег. Основой для сравнения стали экспериментальные данные, полученные в Большом волновом канале (Ганновер, Германия) в 2012–2013 гг. В ходе эксперимента использовались различные типы волн, включая одиночные волны положительной полярности, регулярные волны, бигармонические волны, а также модулированные по частоте и амплитуде волновые пакеты, характерные для волн от скоростных судов. Все рассматриваемые волны имели один и тот же период (характерную длительность) основного сигнала, равный 20 с и соответствующий условиям мелкой воды.

Показано, что обе модели одинаково хорошо справляются с описанием (почти линейных) волн очень малой амплитуды, в то время как для более нелинейных волн большей амплитуды дисперсионная теория показала себя более адекватной моделью, и является более предпочтительной. Подчеркнем, что данные выводы сохраняются для всех рассмотренных типов волн.

Численные расчеты частотно модулированных волн выполнены при финансовой поддержке Российского научного фонда (грант 16-17-00041), расчеты других типов волн выполнены при поддержке гранта РФФИ 18-05-80019 и PUT1378. Экспериментальные данные были получены в рамках проекта Hydralab IV, грант HyIV-FZK-03. Авторы также благодарны программе PHC PARROT грант No 37456YM за поддержку научных визитов во Францию и Эстонию.

Список литературы

  1. Madsen P.A., Banijamali B., Schäffer H.A., Sørensen O.R. Boussinesq type equations with high accuracy in dispersion and nonlinearity // In Edge B (ed.) 25th Conference 1996. ASCE. Coastal Engineering. Hørsholm, 1997. V. 1. P. 95–108.

  2. Bellotti G., Brocchini M. On using Boussinesq-type equations near the shoreline: a note of caution // Ocean Engineering. 2002. V. 29. № 12. P. 1569–1575.

  3. Horrillo J., Kowalik Z., Shigihara Y. Wave dispersion study in the Indian Ocean-tsunami of December 26, 2004 // Marine Geodesy. 2006. V. 29. № 3. P. 149–166.

  4. Glimsdal S., Pedersen G.K., Harbitz C.B., Løvholt F. Dispersion of tsunamis: does it really matter? // Nat. Hazards Earth Syst. Sci. 2013. V. 13. P. 1507–1526.

  5. Løvholt F., Pedersen G., Bazin S., Kühn D., Bredesen R.E., Harbitz C. Stochastic analysis of tsunami runup due to heterogeneous coseismic slip and dispersion // J. Geophysical Research: Oceans. 2012. V. 117. P. C03047.

  6. Candella R.N., Rabinovich A.B., Thomson R.E. The 2004 Sumatra tsunami as recorded on the Atlantic coast of South America // Advances in Geosciences. 2008. V. 14. P. 117–128.

  7. Watada S., Kusumoto S., Satake K. Travel time delay and initial phase reversal of distant tsunamis coupled with the self-gravitating elastic // Earth. J. Geophys. Res. Solid Earth. 2014. V. 119. P. 4287–4310.

  8. Denissenko P., Didenkulova I., Rodin A., Listak M., Pelinovsky E. Experimental statistics of long wave runup on a plane beach // J. Coastal Research. 2013. V. 65. P. 195–200.

  9. Didenkulova I., Denissenko P., Rodin A., Pelinovsky E. Effect of asymmetry of incident wave on the maximum runup height // J. Coastal Research. 2013. V. 65. P. 207–212.

  10. Schimmels S., Sriram V., Didenkulova I. Tsunami generation in a large scale experimental facility // Coastal Engineering. 2016. V. 110. P. 32–41.

  11. Schmidt-Koppenhagen R., Gerdes M., Tautenhain E., Grune J. Online absorption control system for wave generation // 3rd International Symposium on Ocean Wave Measurements and Analysis (WAVES’97). November 1997. Virginia Beach, Virginia, USA, 1997. 11 p.

  12. Torsvik T., Didenkulova I., Soomere T., Parnell K. Variability in spatial patterns of long nonlinear waves from fast ferries in Tallinn Bay // Nonlinear Processes in Geophysics. 2009. V. 16. P. 351–363.

  13. Torsvik T., Soomere T., Didenkulova I., Sheremet A. Identification of ship wake structures by a time-frequency method // J. Fluid Mechanics. 2015. V. 765. P. 229–251.

  14. Durán A., Dutykh D., Mitsotakis D. Peregrine’s System Revisited // In Abcha N., Pelinovsky E., Mutabazi I. (eds.) Nonlinear Waves and Pattern Dynamics. Springer, Cham. 2018. P. 3–43.

  15. Manning R. On the flow of water in open channels and pipes // Transactions of the Institution of Civil Engineers of Ireland. 1891. V. 20. P. 161–207.

  16. https://www.engineeringtoolbox.com/mannings-roughness-d_799.html

  17. Бернацкий А.В., Носов М.А. Роль донного трения в моделях наката на берег необрушающихся длинных волн цунами // Изв. РАН. Физика атмосферы и океана. 2012. Т. 48. № 4. С. 481–486.

  18. Petcu M., Temam R. The one-dimensional shallow water equations with transparent boundary conditions // Math. Meth. Appl. Sci. 2013. V. 36. P. 1979–1994.

  19. Bogacki P., Shampine L.F. A 3(2) pair of Runge-Kutta formulas // Appl. Math. Letters. 1989. V. 2. P. 321–325.

  20. Shampine L.F., Reichelt M.W. The MATLAB ODE Suite // SIAM J. Scientific Computing. 1997. V. 18. P. 1–22.

  21. Dutykh D., Katsaounis T., Mitsotakis D. Finite volume schemes for dispersive wave propagation and runup // J. Computational Physics. 2011. V. 230. № 8. P. 3035–3061.

  22. Диденкулова И.И., Заибо Н., Куркин А.А., Пелиновский Е.Н. Крутизна и спектр нелинейно деформируемой волны на мелководье // Изв. РАН. Физика атмосферы и океана. 2006. Т. 42. № 6. С. 839–842.

  23. Диденкулова И.И., Пелиновский Е.Н., Диденкулова О.И. Накат длинных уединенных волн различной полярности на плоский откос // Изв. РАН. Физика атмосферы и океана. 2014. Т. 50. № 5. С. 604–611.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал