Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 5, стр. 561-566

Моделирование подковообразных волн в рамках квазитрехмерных уравнений движения

А. С. Досаев^*

Институт прикладной физики РАН БОКС-120
603950 г. Нижний Новгород, ул. Ульянова, 46, Россия

Поступила в редакцию 26.03.2019
После доработки 23.03.2020
Принята к публикации 03.06.2020

DOI: 10.31857/S000235152005003X

Аннотация

Статья посвящена исследованию свойств и границ применимости квазитрехмерной модели потенциальных волн – перспективного метода моделирования волн на воде, предложенного В.П. Рубаном и основанного на приближении узкой направленности спектра волнения. В рамках приближенных уравнений движения воспроизведен анализ устойчивости волны Стокса конечной амплитуды по отношению к трехмерным возмущениям. Исследована зона неустойчивости в окрестности резонансной кривой, соответствующей 5-волновым взаимодействиям. Показано, что значения инкремента оказываются близки к точным несмотря на то, что соответствующие моды неустойчивости состоят из гармоник, далеких от главного направления. Последующие стадии развития неустойчивости правдоподобно воспроизводят динамику формирования подковообразной волны. Предложена модификация кубических компонент функционала Гамильтона модели, устраняющая нефизичную зону неустойчивости для возмущений, распространяющихся почти перпендикулярно к основной волне.

Ключевые слова: волны на воде, нелинейные волны, потенциальное течение, конформные переменные

ВВЕДЕНИЕ

Многие характерные особенности динамики волн на воде могут быть объяснены в рамках модели потенциального течения несжимаемой жидкости со свободной поверхностью. Потенциальное течение представляет собой объект, удобный как для аналитического изучения, так и для численного моделирования, поскольку его движение описывается интегро-дифференциальными уравнениями на границе жидкости, и это снижает размерность задачи.

Для численного моделирования двумерных потенциальных волн широко применяется метод конформных преобразований. В конформных координатах уравнения движения записываются таким образом (см., например, [1]), что вычислительная сложность нахождения соответствующих правых частей на пространственной сетке из $N$ узлов определяется сложностью быстрого преобразования Фурье $O\left( {N{\text{lg}}N} \right)$. К преимуществам подхода относится также возможность описывать конфигурации с загибом свободной поверхности (когда возвышение не является однозначной функцией горизонтальной координаты) – кроме очевидного примера обрушающихся волн, такая ситуация также возможна и для необрушающихся волн гравитационно-капиллярного диапазона [2]. Обзор истории метода и подробная библиография могут быть найдены в [3].

Для моделирования трехмерных волн на основе точных уравнений движения может применяться метод поверхностных интегралов [4, 5], который, однако, обладает довольно высокой сложностью. Еще один подход к точному моделированию потенциальных волн подразумевает решение уравнения Лапласа для потенциала на трехмерной сетке [6], при этом требуя, чтобы свободная поверхность не имела загибов.

Квазитрехмерная модель волнения, предложенная В.П. Рубаном [7], представляет собой обобщение метода конформных преобразований для трехмерных течений. Как и полностью нелинейные двумерные модели, она не накладывает ограничений на крутизну волн, однако использует приближение узкой направленности спектра волнения. Комплексная координата вводится в вертикальной плоскости, содержащей “главное” направление распространения волн; в перпендикулярном к этой плоскости направлении изменение всех полей считается медленным. Теория возмущений в общей формулировке для волн над дном произвольной формы, а также частный случай волн на глубокой воде описаны в [7]. В работах [8, 9] модель применяется для изучения влияния трехмерных эффектов на процесс образования волн-убийц. В тех же работах предлагаются варианты регуляризации приближенных уравнений, позволяющие получить корректное дисперсионное соотношение для линейных волн, распространяющихся под любым углом.

Представляет интерес вопрос о границах применимости модели Рубана. Соответствующая теория возмущений использует малый параметр $\epsilon = {{\left( {{{{{l}_{x}}} \mathord{\left/ {\vphantom {{{{l}_{x}}} {{{l}_{q}}}}} \right. \kern-0em} {{{l}_{q}}}}} \right)}^{2}} \ll 1$, где ${{l}_{x}}$, ${{l}_{q}}$ – характерные масштабы длины по главному и поперечному направлениям соответственно. Учет уже первых поправок по $\epsilon $ приводит к уравнениям, которые довольно громоздки и сложны для анализа, что затрудняет оценку точности приближения. Какие трехмерные эффекты сохранены в приближенных уравнениях? Может ли в рамках модели быть описана динамика существенно трехмерного процесса образования подковообразных волн [10]?

В настоящей работе для ответа на эти вопросы сделана попытка в рамках приближенных уравнений модели Рубана воспроизвести анализ устойчивости волны Стокса по отношению к трехмерным возмущениям [11]. Исследована зона неустойчивости, связанная с 5-волновыми взаимодействиями, проведено сравнение значений инкремента с точными значениями из [11]. Показано, что развитие неустойчивости приводит к генерации подковообразных структур.

Для практического применения важно, чтобы квазитрехмерная модель вела себя устойчиво при наличии возмущений, распространяющихся под большими углами к главному направлению, даже если мы не претендуем на корректное описание их динамики. В данной работе предлагается модификация уравнений модели, устраняющая нефизичную зону неустойчивости для возмущений, распространяющихся почти перпендикулярно к основной волне.

ОСНОВНЫЕ УРАВНЕНИЯ

Рассмотрим задачу о потенциальном течении несжимаемой жидкости со свободной поверхностью. Будем использовать декартову систему координат $\left( {x,q,y} \right)$, где ось $y$ направлена вверх. Уравнения движения для потенциала скорости $\varphi \left( {x,q,y,t} \right)$ и свободной поверхности $y = \eta \left( {x,q,t} \right)$ записываются как

$\begin{array}{*{20}{c}} {\Delta \varphi = 0,} \\ {{{\eta }_{t}} + {{\eta }_{x}}{{\varphi }_{x}} + {{\eta }_{q}}{{\varphi }_{q}} - {{\varphi }_{y}} = 0\,\,\,\,\left( {{\text{при}}\,\,\,\,y = \eta } \right),} \\ {{{\varphi }_{t}} + g\eta + \frac{1}{2}{{{\left| {\nabla \varphi } \right|}}^{2}} = 0\,\,\,\,\left( {{\text{при}}\,\,\,\,y = \eta } \right),} \end{array}$

где $g$ – ускорение свободного падения. Ограничимся случаем глубокой воды:

$\left| {\nabla \varphi } \right| \to 0{\text{\;}}\,\,\,\,{\text{при}}\,\,\,\,y \to - \infty .$

Свободная поверхность может быть выпрямлена переходом от пары декартовых координат $\left( {x,y} \right)$ к конформным координатам $\left( {u,v} \right)$. Разумеется, конформное преобразование будет зависеть от оставшейся координаты $q$:

$x + iy = Z\left( {u + iv,q,t} \right),$

где функция $Z$ является аналитической в нижней полуплоскости комплексной переменной $u + iv$. Свободная поверхность при этом параметризуется действительной осью $v = 0$:

$Z\left( {u + i0,q,t} \right) = x\left( {u,q,t} \right) + i\eta \left( {x\left( {u,q,t} \right),q,t} \right).$

При таком описании состояние системы определяется значениями потенциала на свободной поверхности $\psi = {{\left. \varphi \right|}_{{y = \eta }}}$ и отображением $Z$. В [7] приводится вывод эволюционных уравнений для неканонической пары переменных $Z$ и $\psi $ из принципа наименьшего действия с функцией Гамильтона

$H = \frac{g}{2}\int {{{\eta }^{2}}dxdq} + K,$

где

$K = \frac{1}{2}\int {dxdq} \int\limits_{ - \infty }^\eta {\left( {\varphi _{x}^{2} + \varphi _{q}^{2} + \varphi _{y}^{2}} \right)} dy$

– функционал кинетической энергии. Следующие соотношения выполняются точно:

(1)

${{Z}_{t}} = i{{Z}_{u}}\left( {1 + i\hat {H}} \right)\left[ {\frac{{{{\delta K} \mathord{\left/ {\vphantom {{\delta K} {\delta \psi }}} \right. \kern-0em} {\delta \psi }}}}{{{{{\left| {{{Z}_{u}}} \right|}}^{2}}}}} \right],$

(2)

$\begin{gathered} {{\psi }_{t}} = - g\Im Z - {{\psi }_{u}}\hat {H}\left[ {\frac{{{{\delta K} \mathord{\left/ {\vphantom {{\delta K} {\delta \psi }}} \right. \kern-0em} {\delta \psi }}}}{{{{{\left| {{{Z}_{u}}} \right|}}^{2}}}}} \right] + \\ + \,\,\Im {{\left\{ {\left( {1 - i\hat {H}} \right)\left[ {2\left( {{{\delta K} \mathord{\left/ {\vphantom {{\delta K} {\delta Z}}} \right. \kern-0em} {\delta Z}}} \right){{Z}_{u}} + \left( {{{\delta K} \mathord{\left/ {\vphantom {{\delta K} {\delta \psi }}} \right. \kern-0em} {\delta \psi }}} \right){{\psi }_{u}}} \right]} \right\}} \mathord{\left/ {\vphantom {{\left\{ {\left( {1 - i\hat {H}} \right)\left[ {2\left( {{{\delta K} \mathord{\left/ {\vphantom {{\delta K} {\delta Z}}} \right. \kern-0em} {\delta Z}}} \right){{Z}_{u}} + \left( {{{\delta K} \mathord{\left/ {\vphantom {{\delta K} {\delta \psi }}} \right. \kern-0em} {\delta \psi }}} \right){{\psi }_{u}}} \right]} \right\}} {{{{\left| {{{Z}_{u}}} \right|}}^{2}}}}} \right. \kern-0em} {{{{\left| {{{Z}_{u}}} \right|}}^{2}}}}, \\ \end{gathered} $

где $\hat {H}$ – преобразование Гильберта.

Трудность заключается в том, что в трехмерной задаче не известно компактного выражения для $K$ в переменных $Z$ и $\psi $. В рамках подхода [7] $K$ приближенно представляется суммой известной двумерной части (точной при ${{\partial }_{q}} = 0$) и трехмерных поправок $F$:

$K = - \frac{1}{2}\int \psi \hat {H}{{\psi }_{u}}dudq + F.$

Учет поправок первого порядка по малому параметру $\epsilon $ дает

(3)

$\begin{gathered} F = \frac{i}{8}\int {\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} \hat {G}\overline {\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} dudq + \\ + \,\,\frac{i}{{16}}\int {\left\{ {\left[ {{{{{{\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)}}^{2}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right]\hat {E}\overline {\left( {Z - u} \right)} } \right.} - \\ - \,\,\left. {\left( {Z - u} \right)\hat {E}\overline {\left[ {{{{{{\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)}}^{2}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right]} } \right\}dudq, \\ \end{gathered} $

где функция $\Psi $ определяется на свободной поверхности как $\Psi \left( u \right) = \left( {1 + i\hat {H}} \right)\psi \left( u \right)$, выражения для операторов $\hat {G}$,$\hat {E}$ будут приведены ниже. Вариационные производные из (1), (2) выражаются как

$\frac{{\delta K}}{{\delta \psi }} = - \hat {H}{{\psi }_{u}} + 2\Re \left[ {\left( {1 - i\hat {H}} \right)\frac{{\delta F}}{{\delta \Psi }}} \right],\,\,\,\,\frac{{\delta K}}{{\delta Z}} = \frac{{\delta F}}{{\delta Z}},$

$\begin{gathered} \frac{{\delta F}}{{\delta \Psi }} = \frac{i}{8}{{Z}_{q}}{{\partial }_{u}}\left[ {\hat {G}\overline {\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} } \right. + \\ \left. { + \,\,\left( {{{\Psi }_{q}} - {{Z}_{q}}{{{{\Psi }_{u}}} \mathord{\left/ {\vphantom {{{{\Psi }_{u}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right)\hat {E}\overline {\left( {Z - u} \right)} } \right] - \\ - \,\,\frac{i}{8}{{Z}_{u}}{{\partial }_{q}}\left[ {\hat {G}\overline {\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} } \right. \\ \left. { + \,\,\left( {{{\Psi }_{q}} - {{{{Z}_{q}}{{\Psi }_{u}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}{{\Psi }_{u}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right)\hat {E}\overline {\left( {Z - u} \right)} } \right], \\ \end{gathered} $

$\begin{gathered} \frac{{\delta F}}{{\delta Z}} = - \frac{i}{8}{{\Psi }_{q}}{{\partial }_{u}}\left[ {\hat {G}\overline {\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} } \right. + \\ \left. { + \,\,\left( {{{\Psi }_{q}} - {{{{Z}_{q}}{{\Psi }_{u}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}{{\Psi }_{u}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right)\hat {E}\overline {\left( {Z - u} \right)} } \right] + \\ + \,\,\frac{i}{8}{{\Psi }_{u}}{{\partial }_{q}}\left[ {\hat {G}\overline {\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} } \right. + \\ \left. { + \,\,\left( {{{\Psi }_{q}} - {{{{Z}_{q}}{{\Psi }_{u}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}{{\Psi }_{u}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right)\hat {E}\overline {\left( {Z - u} \right)} } \right] \\ + \,\,\frac{i}{{16}}\left[ {{{\partial }_{u}}\left[ {{{{\left( {{{\Psi }_{q}} - {{{{Z}_{q}}{{\Psi }_{u}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}{{\Psi }_{u}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right)}}^{2}}\hat {E}\overline {\left( {Z - u} \right)} } \right]} \right. - \\ \left. { - \,\,\hat {E}\overline {{{{\left( {{{\Psi }_{q}} - {{{{Z}_{q}}{{\Psi }_{u}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}{{\Psi }_{u}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right)}}^{2}}{{Z}_{u}}} } \right]. \\ \end{gathered} $

В оригинальных уравнениях, получаемых по теории возмущений,

$\hat {G} = \partial _{u}^{{ - 1}},\,\,\,\,\hat {E} = 1.$

Для линейных волн это дает дисперсионное соотношение

${{\omega }^{2}} = g\left| k \right|\left( {1 + \frac{{{{m}^{2}}}}{{2{{k}^{2}}}}} \right),$

где $k,m$ – компоненты волнового вектора по осям $x$ и $q$. Для устранения нефизичной особенности в окрестности прямой $k = 0$ в [8, 9] предлагаются различные варианты регуляризации, дающие правильное дисперсионное соотношение на всей плоскости волновых векторов:

(5)

${{\omega }^{2}}\left( {k,m} \right) = g\sqrt {{{k}^{2}} + {{m}^{2}}} .$

Таким образом, регуляризация обеспечивает правильное положение резонансных кривых для нелинейных взаимодействий. В настоящей работе используется вариант

$\begin{gathered} G\left( {k,m} \right) = \frac{{ - 2i}}{{\sqrt {{{m}^{2}} + {{k}^{2}}} + \left| k \right|}}, \\ E\left( {k,m} \right) = \frac{{2\left| k \right|}}{{\sqrt {{{m}^{2}} + {{k}^{2}}} + \left| k \right|}}. \\ \end{gathered} $

УСТРАНЕНИЕ НЕУСТОЙЧИВОСТИ ДЛЯ ПОЧТИ ПЕРПЕНДИКУЛЯРНЫХ ГАРМОНИК

Нас будет интересовать способность приближенных уравнений описывать формирование подковообразных структур на поперечно модулированных волнах большой крутизны. На практике проследить развитие этого процесса, используя оригинальные уравнения модели Рубана, не удается – после определенного момента счет оказывается невозможно продолжать из-за интенсивной генерации поперечной ряби. Пример профиля волны с развивающейся рябью приведен на рис. 1.

Рис. 1.

Генерация поперечной ряби на волне Стокса в результате развития нефизичной неустойчивости квазитрехмерной модели. Начальная крутизна волны Стокса ak = 0.3.

В рамках регуляризованных уравнений волна Стокса оказывается неустойчивой к коротковолновым поперечным возмущениям, и для больших волновых чисел $m$ возмущения инкремент растет как ${{\gamma }_{{k,m}}} \sim \left| m \right|$. Данная нефизичная неустойчивость связана с кубическими слагаемыми в трехмерной части функции Гамильтона (3)

$\frac{i}{{16}}\int {\left\{ {\Psi _{q}^{2}\hat {E}\overline {\left( {Z - u} \right)} - \left( {Z - u} \right)\hat {E}\overline {\Psi _{q}^{2}} } \right\}} dudq.$

Неустойчивость проявляется только в модели с регуляризацией, что, однако, обусловлено не выбором вида оператора $\hat {E}$ (при условии, что $E\left( {k,0} \right) = 1$), а скорее переходом от искаженного дисперсионного соотношения (4) к правильному (5). Неустойчивы только гармоники с продольным волновым числом $k < {{k}_{0}}$, где ${{k}_{0}}$ – волновое число волны Стокса; это объясняется тем, что для прочих возмущений соответствующие квадратичные слагаемые в ${{\delta K} \mathord{\left/ {\vphantom {{\delta K} {\delta \psi }}} \right. \kern-0em} {\delta \psi }}$ отсекаются оператором $\left( {1 - i\hat {H}} \right)$.

Для устранения неустойчивости предлагается следующая модификация функционала $F$:

(6)

$\begin{gathered} F = \frac{i}{8}\int {\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} \hat {G}\overline {\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} dudq + \\ + \,\,\frac{i}{{16}}\int {\left\{ {\left[ {{{{{{\left( {\hat {M}\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {\hat {M}\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} \right)}}^{2}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right] \times } \right.} \\ \times \,\,\hat {E}\overline {\left( {Z - u} \right)} - \left( {Z - u} \right) \times \\ \times \,\,\hat {E}\left. {\overline {\left[ {{{{{{\left( {\hat {M}\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {\hat {M}\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} \right)}}^{2}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right]} } \right\}dudq, \\ \end{gathered} $

где оператор $\hat {M}$ маскирует компоненты спектра, близкие к оси $q$:

$M\left( {k,m} \right) = 1 - {{\left| {\frac{m}{{\sqrt {{{k}^{2}} + {{m}^{2}}} }}} \right|}^{p}}.$

Выбор степени$p$ определяется необходимостью перекрытия маской зоны неустойчивости, в настоящей работе принято $p = 32$. Вариационные производные от (6) равны

$\begin{gathered} \frac{{\delta F}}{{\delta \Psi }} = \frac{i}{8}{{Z}_{q}}{{\partial }_{u}}\left[ {\hat {G}\overline {\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} } \right. + \\ \left. { + \,\,\hat {M}\left( {\left[ {\hat {M}{{\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right]\hat {E}\overline {\left( {Z - u} \right)} } \right)} \right] - \\ - \,\,\frac{i}{8}{{Z}_{u}}{{\partial }_{q}}\left[ {\hat {G}\overline {\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} } \right. + \\ \left. {\,\, + \left( {{{\Psi }_{q}} - {{{{Z}_{q}}{{\Psi }_{u}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}{{\Psi }_{u}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right)\hat {E}\overline {\left( {Z - u} \right)} } \right], \\ \end{gathered} $

$\begin{gathered} \frac{{\delta F}}{{\delta Z}} = - \frac{i}{8}{{\Psi }_{q}}{{\partial }_{u}}\left[ {\hat {G}\overline {\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} } \right. + \\ \left. { + \,\,\left( {{{\Psi }_{q}} - {{{{Z}_{q}}{{\Psi }_{u}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}{{\Psi }_{u}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right)\hat {E}\overline {\left( {Z - u} \right)} } \right] + \\ + \,\,\frac{i}{8}{{\Psi }_{u}}{{\partial }_{q}}\left[ {\hat {G}\overline {\left( {{{Z}_{u}}{{\Psi }_{q}} - {{Z}_{q}}{{\Psi }_{u}}} \right)} } \right. + \\ \left. { + \,\,\left( {{{\Psi }_{q}} - {{{{Z}_{q}}{{\Psi }_{u}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}{{\Psi }_{u}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right)\hat {E}\overline {\left( {Z - u} \right)} } \right] + \\ + \,\,\frac{i}{{16}}\left[ {{{\partial }_{u}}\left[ {{{{\left( {{{\Psi }_{q}} - {{{{Z}_{q}}{{\Psi }_{u}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}{{\Psi }_{u}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right)}}^{2}}\hat {E}\overline {\left( {Z - u} \right)} } \right]} \right. - \\ \left. { - \,\,\hat {E}\overline {{{{\left( {{{\Psi }_{q}} - {{{{Z}_{q}}{{\Psi }_{u}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}{{\Psi }_{u}}} {{{Z}_{u}}}}} \right. \kern-0em} {{{Z}_{u}}}}} \right)}}^{2}}{{Z}_{u}}} } \right]. \\ \end{gathered} $

В следующем разделе будет продемонстрировано, что описанная модификация устраняет обсуждаемую неустойчивость.

АНАЛИЗ УСТОЙЧИВОСТИ ВОЛНЫ СТОКСА

Рассмотрим задачу об устойчивости волны Стокса конечной амплитуды, распространяющейся вдоль оси $x$, по отношению к малым трехмерным возмущениям. Система уравнений (1), (2) слишком громоздка для аналитического исследования, поэтому мы будем исследовать ее численно как абстрактное эволюционное уравнение

$\dot {X} = f\left( X \right)$

для вектора состояния X = $\left\{ {\Re {{Z}_{{km}}}{\kern 1pt} ;\Im {{Z}_{{km}}}{\kern 1pt} ;} \right.$ $\left. {\Re {{\psi }_{{km}}}{\kern 1pt} ;\Im {{\psi }_{{km}}}} \right\}$, компоненты которого определяют амплитуды гармоник $Z$ и $\psi $ в конформных координатах.

Для нахождения точного профиля волны Стокса в конформных координатах используется система уравнений из [1], которая решается при помощи итерационной процедуры. Будем работать в системе отсчета, движущейся с фазовой скоростью основной волны. Тогда соответствующий волне Стокса вектор состояния ${{X}_{0}}$ является стационарным решением:

$f\left( {{{X}_{0}}} \right) = 0.$

Линеаризуя уравнения движения в окрестности ${{X}_{0}}$

${{\dot {X}}_{p}} = f\left( {{{X}_{0}} + {{X}_{p}}} \right) \approx \hat {A}{{X}_{p}}$

и решая задачу о собственных значениях матрицы $\hat {A}$ мы можем найти собственные моды волны Стокса. Компоненты матрицы оцениваются численно путем вычисления $f\left( {{{X}_{0}} + {{X}_{p}}} \right)$ для различных малых приращений ${{X}_{p}}$. Из трансляционной симметрии уравнений (1)–(2) следует, что отличными от нуля могут быть только те матричные элементы $\hat {A}$, которые соответствуют взаимодействию гармоник с волновыми числами

$k = n{{k}_{0}} \pm \Delta k,\,\,\,\,m = \pm \Delta m$,

для некоторых фиксированных $\Delta k$, $\Delta m$. Здесь ${{k}_{0}}$ – волновое число волны Стокса, $n$ – целое число.

Решение задачи на собственные значения матрицы $\hat {A}$ дает набор собственных чисел ${{\gamma }_{i}}$ и собственных векторов${{X}_{i}}$, собственные вектора с $\Re \gamma > 0$ соответствуют неустойчивым модам. Чтобы сопоставить моде ${{X}_{i}}$ определенный волновой вектор, амплитуды гармоник конформного отображения ${{Z}_{{km}}}$ пересчитываются в амплитуды гармоник возвышения ${{\eta }_{{km}}}$ в декартовых координатах $\left( {x,q} \right)$, и выбирается волновой вектор гармоники с наибольшей амплитудой ${{\eta }_{{km}}}$. Пересчет в декартовы координаты необходим потому, что при большой крутизне волны Стокса искажения, вносимые конформным преобразованием, делают получаемую картину зон неустойчивости сложной для интерпретации.

На рис. 2 показаны зоны неустойчивости на плоскости волновых векторов для волны Стокса с крутизной $a{{k}_{0}} = 0.3$. Для сравнения изображены также резонансные кривые

$\begin{gathered} \omega \left( {k,m} \right) + \omega \left( {n{{k}_{0}} - k, - m} \right) = n\omega \left( {{{k}_{0}},0} \right), \\ n = 2,3. \\ \end{gathered} $

Рис. 2.

Зоны неустойчивости на плоскости волновых векторов возмущений, расчитанные в рамках a) оригинальной и б) модифицированной модели. Крутизна основной волны ak₀ = 0.3. Пунктиром изображены резонансные кривые, соответствующие 4- и 5-волновым взамодействиям.

Рисунок 2 а показывает результаты анализа для оригинальной модели, рис. 2 б – для модификации (6). Можно видеть, что в оригинальной модели волна Стокса обладает нефизичной зоной неустойчивости в окрестности оси $q$, которая устраняется модификацией.

Качественно положение и форма зон неустойчивости хорошо согласуются с результатами [11]. Количественное сравнение для инкремента и поперечного волнового числа наиболее неустойчивой моды в зоне, соответствующей 5-волновым взаимодействиям, проведено на рис. 3 и рис. 4 соответственно. Полученные результаты позволяют расчитывать на удовлетворительное описание квазитрехмерной моделью процесса формирования подковообразных волн. На рис. 5 показаны подковообразные структуры, развивающиеся на волне Стокса из малого возмущения в ходе численного моделирования с использованием модифицированных (6) уравнений.

Рис. 3.

Максимальный инкремент трехмерной неустойчивости в зависимости от крутизны основной волны. Сплошная линия – результаты расчета в рамках квазитрехмерной модели. Белые маркеры – данные из работы [11], пунктирные линии – интерполяция.

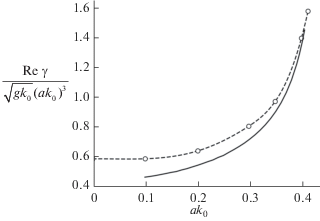
Рис. 4.

Положение максимума инкремента в зоне трехмерной неустойчивости в зависимости от крутизны основной волны. Сплошная линия – результаты расчета в рамках квазитрехмерной модели. Белые маркеры – данные из работы [11].

Рис. 5.

Подковообразные структуры на волне Стокса с начальной крутизной ak = 0.33.

ЗАКЛЮЧЕНИЕ

В работе исследована способность квазитрехмерной модели Рубана воспроизводить существенно трехмерные эффекты, такие как формирование подковообразных волн. Описана модификация функционала Гамильтона модели, ослабляющая трехволновые взаимодействия для гармоник, почти перпендикулярных к основному направлению, и направленная на обеспечение ее более устойчивого поведения при моделировании конфигураций, не удовлетворяющих условию узкой направленности спектра. В рамках приближенных уравнений модели проведен анализ устойчивости волны Стокса. Форма и положение зон неустойчивости хорошо согласуются с результатами расчетов [11] на основе точных уравнений, наблюдаемые значения инкремента близки к точным значениям.

Работа выполнена при поддержке РФФИ в рамках проекта № 18-35-00658.

Список литературы

Dyachenko A.I., Zakharov V.E., Kuznetsov E.A. Nonlinear dynamics of the free surface of an ideal fluid // Plasma Physics Reports. 1996. V. 20. № 10. P. 829–840.
Fedorov A.V., Melville W.K. Nonlinear gravity-capillary waves with forcing and dissipation // J. Fluid Mech. 1998. V. 354. P. 1–42.
Chalikov D.V. Numerical modeling of sea waves. Springer, 2016.
Clamond D., Grue J. A fast method for fully nonlinear water-wave computations // J. Fluid. Mech. 2001. V. 447. P. 337–355.
Fochesato C., Dias F. A fast method for nonlinear three-dimensional free-surface waves // Proc. Roy. Soc. A. 2006. V. 462. 2073. P. 2715–2735.
Chalikov D., Babanin A.V., Sanina E. Numerical modeling of 3d fully nonlinear potential periodic waves // Ocean Dynamics. 2014. V. 64. № 10. P. 1469–1486.
Ruban V.P. Quasiplanar steep water waves // Phys. Rev. E. 2005. V.71. 5:055303.
Ruban V.P., Dreher J. Numerical modeling of quasiplanar giant water waves // Phys. Rev. E. 2005. V. 72. 6:066303
Ruban V.P. Conformal variables in the numerical simulations of long-crested rogue waves // The European Physical J. Special Topics. 2010. V. 185. № 1. P. 17–33.
Su M.-Y. Three dimensional deep-water waves. Part 1. experimental measurement of skew and symmetric wave patterns // J. Fluid Mech. 1982. № 124. P. 73–108.
McLean J.W. Instabilities of finite-amplitude water waves // J. Fluid Mech. 1982. V. 114. P. 315–330.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал