Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 5, стр. 514-525
Экмановское трение и формирование верхнетропосферных зональных течений
a Институт физики атмосферы им. А.М. Обухова РАН
109017 Москва, Пыжевский пер., 3, Россия
b НПО “Тайфун”
249038 Калужская обл., г. Обнинск, ул. Победы, 4, Россия
* E-mail: kalashnik-obn@mail.ru
Поступила в редакцию 03.03.2020
После доработки 12.05.2020
Принята к публикации 03.06.2020
Аннотация
В рамках квазигеострофической модели атмосферы с двумя горизонтальными границами (подстилающей поверхностью и тропопаузой) исследовано влияние экмановского трения на динамику зональных течений (ЗТ). Предполагается, что течения имеют нулевую потенциальную завихренность и вызываются заданными распределениями плавучести на границах. Показано, что в случае периодических распределений разнонаправленный по вертикали профиль скорости ЗТ трансформируется в однонаправленный профиль с максимумом на верхней границе и нулевой скоростью на нижней границе. В процессе трансформации скорость на верхней границе возрастает, т.е. происходит интенсификация верхнетропосферных ЗТ за счет экмановского трения. Аналогичная интенсификация происходит и в случае начальных распределений плавучести фронтального типа, индуцирующих систему из двух противоположно направленных струйных течений, расположенных в верхней и нижней половине слоя атмосферы. За счет экмановского трения осевая скорость нижнего течения падает до нуля, а скорость верхнего течения, постепенно охватывающего всю тропосферу, вырастает в два раза. Результирующее течение представляет собой прижатую к верхней границе струю, которую можно считать прототипом западного верхнетропосферного струйного течения. Важные структурные особенности такой струи, устанавливаемые в рамках полной негеострофической модели, связаны с горизонтальной асимметрией струи и формированием фронтов (поверхностей разрыва), примыкающих к верхней границе.
1. ВВЕДЕНИЕ
В геофизической гидродинамике атмосферу традиционно представляют слоем страфицированной вращающейся жидкости, заключенным между двумя горизонтальными границами – подстилающей поверхностью и тропопаузой [1–4]. Трение о подстилающую поверхность (поверхность Земли) приводит к формированию здесь экмановского пограничного слоя, который, посредством механизма “экмановской подкачки”, оказывает важное влияние на динамику и устойчивость атмосферных течений [5–9]. Обычно считается, что этот механизм приводит к затуханию движений в свободной атмосфере. В действительности это не так – затухают лишь движения непосредственно у поверхности. Вблизи верхней границы (тропопаузы) скорость не подвержена влиянию экмановского трения и определяется меридиональным распределением температуры. С данной особенностью может быть связано существование интенсивных верхнетропосферных струйных течений, расположенных на высоте $8{\kern 1pt} - {\kern 1pt} 10\,\,{\text{км}}$ (уровне тропопаузы) и впервые обнаруженных военными летчиками в конце Второй мировой войны [10, 11]. Максимальная скорость струйных течений может достигать $100\,\,{\text{м/c}}$, т.е. практически на порядок превышать скорость ветра у поверхности Земли. Столь резкий рост скорости в пределах тропосферы, очевидно, не может объясняться падением фоновой плотности атмосферы с высотой (вертикальный масштаб изменения плотности порядка $100\,\,{\text{км}}$).
В настоящей работе исследован процесс трансформации зональных атмосферных течений (ЗТ) за счет придонного экмановского трения. Исследование выполнено в рамках так называемой поверхностной геострофической модели (SQG model, [12–14]), описывающей квазигеострофические течения с нулевой потенциальной завихренностью. Динамика таких течений инициируется заданными распределениями плавучести (потенциальной температуры) на границах. С использованием точных решений модели показано, что в случае периодических по горизонтальной координате распределений разнонаправленный по вертикали профиль скорости ЗТ трансформируется в однонаправленный профиль с максимумом на верхней границе и нулевой скоростью на нижней границе. В процессе трансформации скорость на верхней границе возрастает, т.е. происходит интенсификация верхнетропосферных ЗТ за счет экмановского трения. Для начальных длинноволновых распределений плавучести фронтального типа в работе построены асимптотические решения, описывающие трансформацию системы из двух противоположно направленных струйных течений, расположенных в верхней и нижней половине слоя. Показано, что за счет придонного трения осевая скорость нижнего течения падает до нуля, а скорость верхнего течения, постепенно охватывающего всю тропосферу, вырастает в два раза. Результирующее течение представляет собой прижатую к верхней границе струю, которую можно считать прототипом западного верхнетропосферного струйного течения. В заключительном разделе статьи исследованы структурные особенности такой струи в рамках полной негеострофической модели. Основные особенности связаны с горизонтальной асимметрией профиля скорости струи и формированием фронтов (поверхностей разрыва), примыкающих к верхней границе.
2. ПОСТАНОВКА ЗАДАЧИ
Рассматривается слой стратифицированной, вращающейся атмосферы с постоянной частотой плавучести $N$ и инерционной частотой $f$, заключенный между двумя твердыми горизонтальными границами $z = 0,\,H$ (подстилающей поверхностью и тропопаузой). В квазигеострофическом приближении движения слоя описываются уравнением переноса потенциальной завихренности (ПЗ) $q$. Безразмерная форма уравнения имеет вид [1–3]
(1)
${{q}_{t}} + \left[ {\psi ,q} \right] = 0,\,\,\,\,q = \Delta \psi = {{\psi }_{{xx}}} + {{\psi }_{{yy}}} + {{\psi }_{{zz}}},$Будем считать верхнюю границу свободной, а нижнюю границу совпадающей с верхней границей экмановского пограничного слоя (традиционно ее переносят на уровень $z = 0$). При этом к уравнению (1) присоединяются краевые условия
(2)
$\begin{gathered} z = 0{\kern 1pt} {\kern 1pt} :\,\,\,\,{{\psi }_{{zt}}} + \left[ {\psi ,{{\psi }_{z}}} \right] + r({{\psi }_{{xx}}} + {{\psi }_{{yy}}}) = 0, \\ z = 1{\kern 1pt} {\kern 1pt} :\,\,\,{{\psi }_{{zt}}} + \left[ {\psi ,{{\psi }_{z}}} \right] = 0. \\ \end{gathered} $Здесь $r = {{{{{\text{E}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \mathord{\left/ {\vphantom {{{{{\text{E}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} {2{\text{Ro}}}}} \right. \kern-0em} {2{\text{Ro}}}}$ – коэффициент придонного трения, ${\text{E}} = {{({{{{h}_{E}}} \mathord{\left/ {\vphantom {{{{h}_{E}}} H}} \right. \kern-0em} H})}^{2}}$ – число Экмана, ${{h}_{E}} = {{\left( {{{2\nu } \mathord{\left/ {\vphantom {{2\nu } f}} \right. \kern-0em} f}} \right)}^{{1/2}}}$ – толщина экмановского пограничного слоя с эффективным коэффициентом турбулентной вязкости $\nu $. В размерных переменных первое краевое условие (2) следует из равенства ${{w}_{g}} = {{w}_{E}}$, где ${{w}_{g}} = - ({f \mathord{\left/ {\vphantom {f {{{N}^{2}}}}} \right. \kern-0em} {{{N}^{2}}}}){{d({{\psi }_{z}})} \mathord{\left/ {\vphantom {{d({{\psi }_{z}})} {dt}}} \right. \kern-0em} {dt}}$ – вертикальная скорость в квазигеострофическом приближении [2–4], ${{w}_{E}} = 0.5{{h}_{E}}{{\Delta }_{2}}\psi $ – значение вертикальной скорости (скорости экмановской подкачки) на верхней границе пограничного слоя. Подробный вывод условий (2) представлен в [2]. Отметим, что для приведенных значений параметров и ${{h}_{E}} = 0.5\,\,{\text{км}}$, коэффициент трения $r = 4$. В отсутствии трения, условия (2) есть уравнения переноса плавучести на горизонтальных границах.
Уравнению (1) удовлетворяют течения с ПЗ $q = 0$. Динамика этих течений, аналогичных потенциальным течениям в классической гидродинамике, описывается решением уравнения Лапласа
с нестационарными краевыми условиями (2). Уравнения (2), (3) представляют собой уравнения поверхностной геострофической модели [12], в которых дополнительно учтено придонное трение. Непосредственно из (2), (3) вытекает уравнение баланса полной энергии(4)
${{E}_{t}} = - r({{\left. {\overline {\psi _{x}^{2} + \psi _{y}^{2})} } \right|}_{{z = 0}}},\,\,\,\,E = \int\limits_0^1 {\overline {\left( {\psi _{x}^{2} + \psi _{y}^{2} + \psi _{z}^{2}} \right)} dz} ,$Отметим, что для решений уравнения Лапласа (3) (гармонических функций) значения функции тока $\psi $ на границах выражаются через граничные значения нормальных производных $\sigma = {{\psi }_{z}}$ (посредством нелокального оператора типа Гильберта). Формально математически, описание трехмерной динамики течений с ПЗ $q = 0$, таким образом, сводится к решению двумерных уравнений (2) на границах. Этим объясняется название поверхностная геострофическая модель (SQG model).
Далее будем рассматривать динамику зональных течений с функцией тока $\psi = \psi (y,z,t)$, не зависящей от продольной координаты $x$. Для таких течений двумерный якобиан в уравнениях (2) обращается в ноль и динамика описывается простыми линейными уравнениями
(6)
$z = 0{\kern 1pt} {\kern 1pt} :\,\,\,\,{{\psi }_{{zt}}} + r{{\psi }_{{yy}}} = 0,\,\,\,\,z = 1{\kern 1pt} {\kern 1pt} :\,\,\,\,{{\psi }_{{zt}}} = 0.$Распределения скорости и плавучести в зональных течениях связаны уравнением термического ветра ${{u}_{z}} = - {{\sigma }_{y}}.$ В качестве начальных условий для уравнений (5), (6) считаем заданными распределения плавучести $\sigma = {{\psi }_{z}}$ на границах $z = 0,1$ в момент времени $t = 0$. Ниже анализируются решения (5), (6) для различных типов этих распределений.
3. СЛУЧАЙ ПЕРИОДИЧЕСКИХ РАСПРЕДЕЛЕНИЙ
Пространственно периодическое решение уравнения Лапласа (5), пропорциональное $\cos (ly)$, можно записать в виде
(7)
$\psi = \left( {{{a}_{2}}(t)\operatorname{ch} (lz) - {{a}_{1}}(t)\operatorname{ch} l(z - 1)} \right){{\cos (ly)} \mathord{\left/ {\vphantom {{\cos (ly)} {l\operatorname{sh} (l)}}} \right. \kern-0em} {l\operatorname{sh} (l)}}.$Здесь ${{a}_{{1,2}}}(t)$ – постоянные интегрирования (амплитуды), зависящие от времени параметрически. Непосредственно из (7) следует
(8)
${{\left. {{{\psi }_{z}}} \right|}_{{z = 0}}} = {{a}_{1}}(t)\cos (ly),\,\,\,\,{{\left. {{{\psi }_{z}}} \right|}_{{z = 1}}} = {{a}_{2}}(t)\cos (ly),$(9)
${{a}_{{1t}}} - r\alpha (l)\left( {{{a}_{2}}{{{\operatorname{ch} }}^{{ - 1}}}(l) - {{a}_{1}}} \right) = 0,\,\,\,\,{{a}_{{2t}}} = 0,$(10)
$\begin{gathered} {{a}_{1}}(t) = {{a}_{2}}(0)\,{\text{ct}}{{{\text{h}}}^{{ - 1}}}(l) + \\ + \,\,\left( {{{a}_{1}}(0) - {{a}_{2}}(0)\,{\text{ct}}{{{\text{h}}}^{{ - 1}}}(l)} \right)\exp ( - r\alpha (l)t). \\ \end{gathered} $Из (10) следует, что ${{a}_{1}}(t) \to {{\bar {a}}_{1}} = {{a}_{2}}(0){{\operatorname{ch} }^{{ - 1}}}(l)$ при $t \to \infty $. Соответственно, из (7) получим $\psi (y,z,t) \to \bar {\psi }(y,z)$, где
(11)
$\bar {\psi }(y,z) = {{a}_{2}}(0)\operatorname{sh} (lz){{\cos (ly)} \mathord{\left/ {\vphantom {{\cos (ly)} {l\operatorname{ch} l}}} \right. \kern-0em} {l\operatorname{ch} l}}.$Таким образом, на больших временах устанавливается предельное периодическое течение с функцией тока (11) и распределениями скорости и плавучести
(12)
$\begin{gathered} \bar {u}(y,z) = \bar {U}(z)\sin (ly),\,\,\,\,\bar {U}(z) = {{a}_{2}}(0){{\operatorname{sh} (lz)} \mathord{\left/ {\vphantom {{\operatorname{sh} (lz)} {\operatorname{ch} l}}} \right. \kern-0em} {\operatorname{ch} l}}, \\ \bar {\sigma }(y,z) = \bar {\Theta }(z)\cos (ly),\,\,\,\,\bar {\Theta }(z) = {{a}_{2}}(0){{\operatorname{ch} (lz)} \mathord{\left/ {\vphantom {{\operatorname{ch} (lz)} {\operatorname{ch} l}}} \right. \kern-0em} {\operatorname{ch} l}}. \\ \end{gathered} $Важная особенность предельного течения состоит в том, что $\bar {u}(y,0) = 0$, т.е. под влиянием экмановского трения устанавливается течение с нулевой скоростью на нижней границе. Скорость на верхней границе $\bar {u}(y,1) = {{a}_{2}}(0)\operatorname{th} (l)\cos (ly)$ отлична от нуля. Обратим внимание, что распределения плавучести и скорости в предельном течении сдвинуты по фазе на ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$.
Общее нестационарное решение для поля скорости можно записать в виде
(13)
$\begin{gathered} u(y,z,t) = U(z,t)\sin (ly), \\ U(z,t) = {{\left( {{{a}_{2}}(0)\operatorname{ch} (lz) - {{a}_{1}}(t)\operatorname{ch} l(z - 1)} \right)} \mathord{\left/ {\vphantom {{\left( {{{a}_{2}}(0)\operatorname{ch} (lz) - {{a}_{1}}(t)\operatorname{ch} l(z - 1)} \right)} {\operatorname{sh} l}}} \right. \kern-0em} {\operatorname{sh} l}}, \\ \end{gathered} $(14)
$U(z,0) = {{a\operatorname{sh} (l(z - 0.5))} \mathord{\left/ {\vphantom {{a\operatorname{sh} (l(z - 0.5))} {\operatorname{ch} (0.5l)}}} \right. \kern-0em} {\operatorname{ch} (0.5l)}}$Рис. 1.
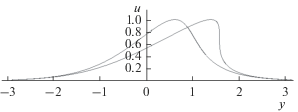
Вертикальные профили скорости $U(z,t)$в моменты времени $t = 0$ (1), $t = 0.1$ (2), $t = 1$ (3) для значения $l = 2$.

Для длинноволновых возмущений ($l \to 0$) финальная скорость на верхней границе $U(1,\infty )\sim 2U(1,0)$ практически в два раза превышает начальную скорость. Экмановское трение, таким образом, приводит к интенсификации течений на верхнем уровне.
В произвольный момент времени смена знака профиля скорости (13) происходит на уровне $z = z{\text{*}}(t)$, где $U(z*,t) = 0$. В случае равных амплитуд ${{a}_{1}}(0) = {{a}_{2}}(0)$ этот уровень находится из уравнения
При $l \to 0$ отсюда асимптотически следует $z = z{\text{*}}(t) = ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}){{e}^{{ - rt}}}$. С течением времени $z{\text{*}}(t) \to 0$, т.е. под действием трения начальное разнонаправленное течение трансформируется в однонаправленное течение с максимумом скорости у верхней границы.
Остановимся кратко на анализе профиля скорости в случае произвольных начальных значений амплитуд ${{a}_{1}}(0),\,{{a}_{2}}(0)$. С использованием (13) эти амплитуды можно выразить через начальные значения скорости на границах
Для предельной скорости на верхней границе $U(1,\infty ) = {{a}_{2}}(0)\operatorname{th} (l)$ отсюда следует
(15)
$\begin{gathered} U(1,\infty ) = U(1,0)\left( {1 + m{{{\operatorname{ch} }}^{{ - 1}}}(l)} \right), \\ m = {{ - U(0,0)} \mathord{\left/ {\vphantom {{ - U(0,0)} {U(1,0)}}} \right. \kern-0em} {U(1,0)}}. \\ \end{gathered} $Согласно (15), для разнонаправленных в начальный момент времени течений ($m > 0$) предельная скорость на верхней границе всегда превосходит начальную скорость, причем значение коэффициента усиления (выражение в круглых скобках) определяется начальным значением скорости $U(0,0)$ на нижней границе (и может быть очень большим). Как и ранее, с течением времени скорость на нижней границе стремится к нулю и на больших временах формируется однонаправленное предельное течение.
Аналогичным образом исследуется вертикальный профиль плавучести
В случае равных граничных амплитуд начальному моменту времени отвечает распределение, симметричное относительно середины слоя $\Theta (z,0) = {{a\operatorname{ch} (l(z - 0.5))} \mathord{\left/ {\vphantom {{a\operatorname{ch} (l(z - 0.5))} {\operatorname{ch} (0.5l)}}} \right. \kern-0em} {\operatorname{ch} (0.5l)}}$ с граничными значениями $\Theta (1,0) = \Theta (0,0) = a$ и значением $\Theta (0.5,0) = $ $ = {a \mathord{\left/ {\vphantom {a {\operatorname{ch} (0.5l)}}} \right. \kern-0em} {\operatorname{ch} (0.5l)}}$. С течением времени плавучесть на нижней границе уменьшается до значения $\Theta (0,\infty ) = {a \mathord{\left/ {\vphantom {a {\operatorname{ch} (l)}}} \right. \kern-0em} {\operatorname{ch} (l)}}$, а плавучесть на верхней границе не меняется. Таким образом, формируется монотонно растущий предельный вертикальный профиль плавучести (12). Отметим, что в предельном состоянии плавучесть на нижней границе отлична от нуля, в отличие от функции тока (возмущения давления), которая пропорциональна полю скорости.
Используя решение (7), можно найти также распределение вертикальной компоненты скорости. В качестве масштаба этой компоненты в квазигеострофической теории традиционно принимается ${{W}_{0}} = {\text{Ro}}({{H{{U}_{0}}} \mathord{\left/ {\vphantom {{H{{U}_{0}}} D}} \right. \kern-0em} D})$ [2–4]. При этом для зональных течений безразмерная компонента $w = {{w}_{g}} = - {{\psi }_{{zt}}}$. С учетом (7) в случае равных амплитуд получим
Максимум $W(z,t)$, достигаемый на нижней границе $z = 0$, представляет собой скорость экмановской подкачки. На верхней границе $W = 0$. По мере установления предельного течения $W(z,t) \to 0$.
Отметим, что под действием экмановского трения движения однородной (нестратифицированной) вращающейся жидкости всегда затухают. Соответствующий процесс затухания исследовался в многочисленных работах [5, 15, 16] и получил специальное название – спиндаун. Как показано выше, для стратифицированной жидкости со свободной верхней границей спиндаун заменяется процессом установления стационарного предельного течения с нулевой скоростью на нижней границе.
Приведем численную оценку характерного времени ${{T}_{E}}$ установления предельного течения. Согласно (7), (10) для периодических течений в качестве этого времени можно взять ${{T}_{E}} = {{(r\alpha (l))}^{{ - 1}}}$ или, в размерных переменных,
(16)
${{T}_{E}} = ({{2H} \mathord{\left/ {\vphantom {{2H} {{{h}_{E}}}}} \right. \kern-0em} {{{h}_{E}}}}){{\alpha }^{{ - 1}}}(l){{f}^{{ - 1}}},\,\,\,\,\alpha (l) = Dl{\kern 1pt} {\kern 1pt} {\text{cth}}(Dl),$Завершая данный раздел, отметим возможность простого анализа динамики зональных течений с ${\text{ПЗ}} \ne 0$. Действительно, для таких течений из (1) следует ${{q}_{t}} = 0$, откуда $q = {{\Delta }_{2}}\psi = {{q}_{i}}(y,z)$, где ${{q}_{i}}(y,z)$ – начальное распределение $q$. Решение последнего уравнения можно представить суммой поверхностного и вихревого компонентов $\psi = {{\psi }^{{(s)}}}(y,z,t) + {{\psi }^{{({\text{v}})}}}(y,z)$. Здесь компонент ${{\psi }^{{(s)}}}$ удовлетворяет уравнению Лапласа (5) с условиями (6). Периодические решения даются выражением (7). Вихревой компонент удовлетворяет уравнению Пуассона ${{\Delta }_{2}}\psi = {{q}_{i}}$ с условиями ${{\psi }^{{({\text{v}})}}} = 0$ и $\psi _{z}^{{{\text{(v)}}}} = 0$ соответственно при $z = 0$ и $z = 1$. Если ${{q}_{i}}(y,z) = F(z)\cos (ly)$ вихревой компонент
4. ПРЕДЕЛЬНОЕ ТЕЧЕНИЕ ДЛЯ РАСПРЕДЕЛЕНИЯ ПЛАВУЧЕСТИ ФРОНТАЛЬНОГО ТИПА
В случае произвольных начальных распределений плавучести под действием придонного трения устанавливается предельное течение с нулевой скоростью на подстилающей поверхности. В силу условий (6) функция тока $\psi (y,z)$ предельного течения находится из решения смешанной краевой задачи для двумерного уравнения Лапласа в полосе $0 < z < 1$
(17)
${{\psi }_{{yy}}} + {{\psi }_{{zz}}} = 0,\,\,\,\,\psi (y,0) = 0,\,\,\,\,{{\psi }_{z}}(y,1) = \sigma (y),$Краевую задачу (17) удобно переформулировать в терминах скорости $u = - {{\psi }_{y}}$ :
(18)
$\begin{gathered} {{u}_{{yy}}} + {{u}_{{zz}}} = 0,\,\,\,\,\,\,u(y,0) = 0, \\ {{u}_{z}}(y,1) = - \sigma {\kern 1pt} '(y) = a{\lambda \mathord{\left/ {\vphantom {\lambda {{{{\operatorname{ch} }}^{2}}}}} \right. \kern-0em} {{{{\operatorname{ch} }}^{2}}}}(\lambda y). \\ \end{gathered} $Для решения этой задачи можно использовать два подхода. Первый подход состоит в использовании интегрального представления решения – свертки заданных граничных распределений с функцией Грина [17]. Второй подход состоит в использовании преобразования Фурье по горизонтальной координате с последующим его обращением. В терминах элементарных функций обратное преобразование Фурье (как и интегральное представление) выражается в случае $\lambda = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, т.е. ситуации, когда ширина переходной зоны порядка две трети от радиуса деформации Россби. Для данного значения $\lambda $ решение задачи (18) и соответствующее распределение плавучести (находится из уравнения термического ветра ${{u}_{z}} = - {{\sigma }_{y}}$)
(19)
$\begin{gathered} u(y,z) = \frac{{a\sin ({{\pi z} \mathord{\left/ {\vphantom {{\pi z} 2}} \right. \kern-0em} 2})}}{{\operatorname{ch} ({{\pi y} \mathord{\left/ {\vphantom {{\pi y} 2}} \right. \kern-0em} 2}) + \cos ({{\pi z} \mathord{\left/ {\vphantom {{\pi z} 2}} \right. \kern-0em} 2})}}, \\ \sigma (y,z) = - \frac{{a\operatorname{sh} ({{\pi y} \mathord{\left/ {\vphantom {{\pi y} 2}} \right. \kern-0em} 2})}}{{\operatorname{ch} ({{\pi y} \mathord{\left/ {\vphantom {{\pi y} 2}} \right. \kern-0em} 2}) + \cos ({{\pi z} \mathord{\left/ {\vphantom {{\pi z} 2}} \right. \kern-0em} 2})}}. \\ \end{gathered} $Распределениям (19) отвечает функция тока предельного течения (возмущение давления)
(20)
$\psi = - \frac{{4a}}{\pi }{\text{arctg}}\left( {\frac{{1 - \cos ({{\pi z} \mathord{\left/ {\vphantom {{\pi z} 2}} \right. \kern-0em} 2})}}{{\sin ({{\pi z} \mathord{\left/ {\vphantom {{\pi z} 2}} \right. \kern-0em} 2})}}\operatorname{th} ({{\pi y} \mathord{\left/ {\vphantom {{\pi y} 4}} \right. \kern-0em} 4})} \right),$Согласно (19) в предельном течении скорость на нижней границе $u(y,0) = 0$, в то время как на верхней границе $u(y,1) = {а \mathord{\left/ {\vphantom {а {\operatorname{ch} ({{\pi y} \mathord{\left/ {\vphantom {{\pi y} 2}} \right. \kern-0em} 2})}}} \right. \kern-0em} {\operatorname{ch} ({{\pi y} \mathord{\left/ {\vphantom {{\pi y} 2}} \right. \kern-0em} 2})}}$. Последнее распределение отвечает локализованному струйному течению. Теневая картина изолиний поля скорости предельного течения представлена на рис. 2. Как следует из рисунка, в случае фронтального распределения температуры за счет придонного трения формируется струйное течение, прижатое к верхней границе. Данное течение можно считать аналогом верхнетропосферного струйного течения в атмосфере Земли.
Простые асимптотические выражения для предельного течения можно получить в случае медленно меняющихся по координате $y$ распределений плавучести на верхней границе ${{\left. {{{\psi }_{z}}} \right|}_{{z = 1}}} = \sigma (\varepsilon y)$, где $\varepsilon \ll 1$. Переходя к медленной переменной $\xi = \varepsilon y$, для функции тока из (17) получим уравнение
с краевыми условиями $\psi (\xi ,0) = 0,$ $\,{{\psi }_{z}}\,(\xi ,1) = \sigma (\xi )$. Решение представляется в форме асимптотического разложенияДля нулевого приближения получим уравнение $\psi _{{zz}}^{{(0)}} = 0$ с приведенными выше краевыми условиями. Ограничиваясь только этим приближением, для предельного течения найдем
(23)
$\begin{gathered} \psi = {{\psi }^{{(0)}}} = \sigma (\xi )z,\,\,\,\,u = - \varepsilon {{\psi }_{\xi }} = - \varepsilon z{{\sigma }_{\xi }}, \\ \sigma = {{\psi }_{z}} = \sigma (\xi ). \\ \end{gathered} $В частности, для распределения фронтального типа $\sigma (\xi ) = - a\operatorname{th} (\lambda \xi )$ скорость течения $u = {{a\lambda \varepsilon z} \mathord{\left/ {\vphantom {{a\lambda \varepsilon z} {{{{\operatorname{ch} }}^{2}}(\lambda \xi )}}} \right. \kern-0em} {{{{\operatorname{ch} }}^{2}}(\lambda \xi )}}$. Согласно последнему выражению скорость линейно растет с высотой. На верхней границе профиль скорости отвечает так называемой струе Бикли. Теневая картина изолиний поля скорости на плоскости $(\xi ,z)$аналогична картине, представленной на рис. 2.
В следующем разделе исследуется нестационарный процесс установления предельного течения.
5. УСТАНОВЛЕНИЕ ПРЕДЕЛЬНОГО ТЕЧЕНИЯ
В рамках длинноволнового приближения можно получить асимптотические решения, описывающие процесс установления предельного течения. Эти решения удовлетворяют уравнению (21) с вытекающими из (6) нестационарными краевыми условиями
(24)
$\begin{gathered} z = 0{\kern 1pt} {\kern 1pt} :\,\,\,\,{{\psi }_{{zt}}} + {{\varepsilon }^{2}}r{{\psi }_{{\xi \xi }}} = 0, \\ z = 1:\,\,\,{{\psi }_{{zt}}} = 0. \\ \end{gathered} $Поскольку в условия (24) входят распределения $\psi ,\,{{\psi }_{z}}$, для построения нестационарных решений нужны формулы, связывающие распределения функции тока и ее нормальной производной на границах полосы. Для получения этих формул, рассмотрим вспомогательную задачу, состоящую в решении уравнения (21) с краевыми условиями
(зависимость от времени параметрическая). Решение вспомогательной задачи ищется в форме асимптотического разложения (22). Нулевое приближение удовлетворяет уравнению $\psi _{{zz}}^{{(0)}} = 0$ с краевыми условиями условиям (25). Отсюда ${{\psi }^{{(0)}}} = \theta (\xi ,t)z + \varphi (\xi ,t).$Первое приближение удовлетворяет уравнению $\psi _{{zz}}^{{(1)}} = - \psi _{{\xi \xi }}^{{(0)}} = - z{{\theta }_{{\xi \xi }}} - {{\varphi }_{{\xi \xi }}}$ с условиями ${{\psi }^{{(1)}}} = 0$ и $\psi _{z}^{{(1)}} = 0$ соответственно при $z = 0$ и $z = \,1$. Отсюда, прямым интегрированием, находится ${{\psi }^{{(1)}}}$. Ограничиваясь двумя первыми приближениями, для функции тока и ее производной, таким образом, найдем
(26)
$\begin{gathered} \psi = \theta z + \varphi + \\ + \,\,{{\varepsilon }^{2}}\left( {\left( {({z \mathord{\left/ {\vphantom {z 2}} \right. \kern-0em} 2}) - ({{{{z}^{3}}} \mathord{\left/ {\vphantom {{{{z}^{3}}} 6}} \right. \kern-0em} 6})} \right){{\theta }_{{\xi \xi }}} + \left( {z - ({{{{z}^{2}}} \mathord{\left/ {\vphantom {{{{z}^{2}}} 2}} \right. \kern-0em} 2})} \right){{\varphi }_{{\xi \xi }}}} \right), \\ {{\psi }_{z}} = \theta + {{\varepsilon }^{2}}\left( {\left( {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}) - ({{{{z}^{2}}} \mathord{\left/ {\vphantom {{{{z}^{2}}} 2}} \right. \kern-0em} 2})} \right){{\theta }_{{\xi \xi }}} + \left( {1 - z} \right){{\varphi }_{{\xi \xi }}}} \right). \\ \end{gathered} $Полагая в (26) $z = 0,\,1$, окончательно получим формулы
(27)
$\begin{gathered} {{\left. \psi \right|}_{{z = 1}}} = \theta + \varphi + {{\varepsilon }^{2}}\left( {({1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}){{\theta }_{{\xi \xi }}} + ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}){{\varphi }_{{\xi \xi }}}} \right), \\ {{\left. {{{\psi }_{z}}} \right|}_{{z = 0}}} = \theta + {{\varepsilon }^{2}}\left( {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}){{\theta }_{{\xi \xi }}} + {{\varphi }_{{\xi \xi }}}} \right), \\ \end{gathered} $С использованием формул (25), (27) краевые условия (24) сводятся к простым уравнениям относительно граничных функций $\theta (\xi ,t),\varphi (\xi ,t)$. Действительно, с учетом (25) второе краевое условие (21) дает ${{\theta }_{t}} = 0$, т.е. $\theta = \theta (\xi ,0)$. При этом из второй формулы (24) следует ${{\left. {{{\psi }_{{zt}}}} \right|}_{{z = 0}}} = {{\varepsilon }^{2}}{{\varphi }_{{\xi \xi }}}$. Подставляя это выражение в первое краевое условие (24) и учитывая (25), после понижения порядка получим уравнение ${{\varphi }_{t}} + r\varphi = 0$. Отсюда
Выражения (26), где $\theta = \theta (\xi ,0)$ и $\varphi (\xi ,t)$ определено (28), таким образом, дают нестационарное (асимптотическое) решение, отвечающее заданным начальным распределениям $\theta (\xi ,0)$, $\varphi (\xi ,0)$.
В качестве примера рассмотрим случай начальных распределений $\theta (\xi ,0)$ = $ - a\operatorname{th} (\lambda \xi ),$ $\varphi (\xi ,0) = ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})a\operatorname{th} (\lambda \xi ).$ Если ограничиться в (26) только первым приближением, то функция тока $\psi = \theta (\xi ,t)z + \varphi (\xi ,t)$ или $\psi = a\operatorname{th} (\lambda \xi )\left( {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}){{e}^{{ - rt}}} - z} \right)$. Соответственно, распределение скорости
(29)
$u = - \varepsilon {{\psi }_{\xi }} = a\varepsilon \lambda {{\left( {z - ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}){{e}^{{ - rt}}}} \right)} \mathord{\left/ {\vphantom {{\left( {z - ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}){{e}^{{ - rt}}}} \right)} {{{{\operatorname{ch} }}^{2}}(\lambda \xi )}}} \right. \kern-0em} {{{{\operatorname{ch} }}^{2}}(\lambda \xi )}}.$Теневые картины изолиний поля скорости $u = u(\xi ,z,t)$ (29) приведены на рис. 3 (для трех моментов времени). В начальный момент времени в верхней половине слоя атмосферы имеется симметричная струя, направленная на восток, в нижней половине слоя – струя, направленная на запад. Максимальные осевые скорости течений ${{u}_{{\max }}} = {{a\varepsilon \lambda } \mathord{\left/ {\vphantom {{a\varepsilon \lambda } 2}} \right. \kern-0em} 2}$ (по модулю) достигаются на верхней и нижней границах. За счет придонного трения, с течением времени осевая скорость нижнего течения падает до нуля, а скорость верхнего течения, постепенно охватывающего всю тропосферу, вырастает в два раза. Согласно (29), смена направления течений происходит на уровне $z = z{\text{*}}(t) = ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}){{e}^{{ - rt}}}$, т.е. $z{\text{*}}(0) = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ и $z* \to 0$ при $t \to \infty $. Таким, образом, на больших временах формируется предельное верхнетропосферное струйное течение со скоростью $u = {{a\varepsilon \lambda z} \mathord{\left/ {\vphantom {{a\varepsilon \lambda z} {{{{\operatorname{ch} }}^{2}}(\lambda \xi )}}} \right. \kern-0em} {{{{\operatorname{ch} }}^{2}}(\lambda \xi )}}$, направленной на восток (западное течение).
Рис. 3.
Теневые картины изолиний поля скорости (29) в плоскости $(\xi ,z)$ для трех моментов времени $t = 0$ (а), $t = 0.2$ (б), $t = 1$ (в).

Аналогично, с использованием решения (26), можно построить картины поля плавучести $\sigma = {{\psi }_{z}}$ и поля вертикальной компоненты скорости $w = - {{\psi }_{{zt}}}$. Отметим, что распределение $w = - ra{{(\varepsilon \lambda )}^{2}}(1 - z){{(\operatorname{sh} (\lambda \xi )} \mathord{\left/ {\vphantom {{(\operatorname{sh} (\lambda \xi )} {{{{\operatorname{ch} }}^{3}}(\lambda \xi )){{e}^{{ - rt}}}}}} \right. \kern-0em} {{{{\operatorname{ch} }}^{3}}(\lambda \xi )){{e}^{{ - rt}}}}}$ несимметрично относительно оси симметрии верхнего струйного течения (в процессе его установления). В северной части струи ($\xi > 0$) имеют место опускание воздуха, в южной части струи ($\xi < 0$) – подъем.
6. ДВОЙНОЙ ЭКМАНОВСКИЙ СЛОЙ
В геофизической гидродинамике часто рассматривают ситуации, когда на верхней (частично свободной) границе слоя атмосферы также имеется пограничный слой, однако с другим коэффициентом трения [7]. В рамках SQG модели двумерные движения слоя (зональные течения) описывается уравнением Лапласа (5) с граничными условиями
(30)
$\begin{gathered} z = 0{\kern 1pt} {\kern 1pt} :\,\,\,\,{{\psi }_{{zt}}} + {{r}_{1}}{{\psi }_{{yy}}} = 0, \\ z = 1{\kern 1pt} {\kern 1pt} :\,\,\,\,{{\psi }_{{zt}}} - {{r}_{2}}{{\psi }_{{yy}}} = 0. \\ \end{gathered} $Здесь ${{r}_{1}},\,{{r}_{2}}$ – коэффициенты трения соответственно на нижней и верхней границах. Отрицательный знак во втором условии учитывает, что скорость экмановской подкачки на верхней границе направлена внутрь слоя.
Рассмотрим вначале случай пространственно периодических решений задачи (5), (30), которые представляются в форме (7). Подстановка (7) в условия (30) дает линейную систему
(31)
$\begin{gathered} {{a}_{{1t}}} - {{r}_{1}}\alpha (l)\left( {{{a}_{2}}{{{\operatorname{ch} }}^{{ - 1}}}(l) - {{a}_{1}}} \right) = 0, \\ {{a}_{{2t}}} + {{r}_{2}}\alpha (l)\left( {{{a}_{2}} - {{a}_{1}}{{{\operatorname{ch} }}^{{ - 1}}}(l)} \right) = 0, \\ \end{gathered} $(32)
$\delta {{a}_{{1\tau }}} - m{{a}_{2}} + {{a}_{1}} = 0,\,\,\,\,{{a}_{{2\tau }}} + {{a}_{2}} - m{{a}_{1}} = 0.$Общее решение (32) есть линейная комбинация экспонент ${{e}^{{{{s}_{{1,2}}}\tau }}}$, удовлетворяющая заданным начальным условиям ${{a}_{1}}(0)$, ${{a}_{2}}(0)$. Здесь ${{s}_{{1,2}}}$ – собственные значения матрицы системы,
(33)
${{s}_{{1,2}}} = {{(2\delta )}^{{ - 1}}}\left( { - (1 + \delta ) \pm \sqrt {{{{(1 + \delta )}}^{2}} - 4\delta {{{\operatorname{th} }}^{2}}(l)} } \right),$Для значений $\delta \ll 1$, когда коэффициент трения на нижней границе много больше коэффициента трения на верхней границе, система (32) представляет собой классическую сингулярно возмущенную систему и для ее решения можно использовать стандартные асимптотические подходы (не привлекая точное решение). Асимптотическое решение имеет вид
(34)
$\begin{gathered} {{a}_{2}}(\tau ) = {{a}_{2}}(0){{e}^{{ - n\tau }}}, \\ {{a}_{1}}(\tau ) = m{{a}_{2}}(0){{e}^{{ - n\tau }}} + \left( {{{a}_{1}}(0) - m{{a}_{2}}(0)} \right){{e}^{{ - \tau /\delta }}}, \\ \end{gathered} $Решению (34) отвечает поле скорости $u(y,z,\tau ) = U(z,\tau )\sin (ly)$, где $U(z,\tau )$ дается выражением (13), в котором ${{a}_{1}}(t)$,${{a}_{2}}(0)$ следует заменить на ${{a}_{1}}(\tau )$, ${{a}_{2}}(\tau )$. В частности, на горизонтальных границах
(35)
$\begin{gathered} U(0,\tau ) = {\text{cth}}(l)\left( {m{{a}_{2}}(\tau ) - {{a}_{1}}(\tau )} \right), \\ U(1,\tau ) = {\text{cth}}(l)\left( {{{a}_{2}}(\tau ) - m{{a}_{1}}(\tau )} \right). \\ \end{gathered} $Непосредственно из (34), (35) следует, что эволюция вертикального профиля скорости связана с двумя временными масштабами. На быстром временном масштабе ${{\tau }_{1}} = \delta $, т.е. (в размерных переменных) масштабе ${{T}_{E}}$, за счет трения о нижнюю границу формируется однонаправленное течение с нулевой скоростью при $z = 0$ . Далее, под действием трения о верхнюю границу, это течение медленно затухает на временном масштабе ${{\tau }_{2}} = {{n}^{{ - 1}}} \gg \delta $. Это прямо следует из асимптотик $U(0,\tau ) = 0$, $U(1,\tau ) = \operatorname{th} (l){{a}_{2}}(0){{e}^{{ - n\tau }}}$ при $\tau \gg \delta $. Отметим, что ${{\tau }_{2}} = {{\operatorname{th} }^{{ - 2}}}(l) \to \infty $ при $l \to 0$, т.е. в случае длинноволновых возмущений затухание практически отсутствует.
Аналогично предыдущему разделу, можно построить асимптотическую теорию, описывающую эволюцию длинноволновых движений, зависящих от координаты $\xi = \varepsilon y$. Эта эволюция описывается решением уравнения (21) с вытекающими из (30) краевыми условиями
(36)
$\begin{gathered} z = 0{\kern 1pt} {\kern 1pt} :\,\,\,\,{{\psi }_{{zt}}} + {{\varepsilon }^{2}}{{r}_{1}}{{\psi }_{{\xi \xi }}} = 0, \\ z = 1{\kern 1pt} {\kern 1pt} :\,\,\,\,{{\psi }_{{zt}}} - {{\varepsilon }^{2}}{{r}_{2}}\,{{\psi }_{{\xi \xi }}} = 0. \\ \end{gathered} $Асимптотическое решение уравнения (21), удовлетворяющее вспомогательным условиям (25), дается выражением (26), содержащим неизвестные функции $\theta (\xi ,t),\,\,\varphi (\xi ,t)$. Подстановка (26) в краевые условия (36), с учетом формул (27), приводит к системе уравнений для нахождения этих функций
(37)
$\begin{gathered} {{\varphi }_{t}} + ({{r}_{1}} + {{r}_{2}})\varphi + {{r}_{2}}\theta = 0, \\ {{\theta }_{t}} - {{\varepsilon }^{2}}{{r}_{2}}\left( {{{\theta }_{{\xi \xi }}} + {{\varphi }_{{\xi \xi }}}} \right) = 0. \\ \end{gathered} $Поскольку $\varepsilon \ll 1$, из второго уравнения асимптотически следует ${{\theta }_{t}} = 0$, т.е. $\theta = \theta (\xi ,0)$. При этом, в случае ${{r}_{1}} \gg {{r}_{2}}$, первое уравнение сводится к ранее полученному уравнению ${{\varphi }_{t}} + {{r}_{1}}\varphi = 0$. Таким образом, в этом случае на процесс затухания длинноволновых движений верхний пограничный слой практически не оказывает влияния.
Отметим, что система (33) сводится к одному уравнению второго порядка
(38)
${{\varphi }_{{tt}}} + ({{r}_{1}} + {{r}_{2}}){{\varphi }_{t}} - {{r}_{2}}{{\varepsilon }^{2}}({{\varphi }_{{t\xi \xi }}} + {{r}_{1}}{{\varphi }_{{\xi \xi }}}) = 0.$Легко проверяется, что данное уравнение имеет пространственно периодические решения $\varphi \sim {{e}^{{s\tau }}}{{e}^{{ik\xi }}}$, $\tau = {{r}_{2}}t$, где значения $s$ даются выражением (33) с учетом $\operatorname{th} (l)\sim l = \varepsilon k$.
7. ПРЕДЕЛЬНОЕ ТЕЧЕНИЕ В НЕГЕОСТРОФИЧЕСКОЙ МОДЕЛИ
Построенное в разделе 4 стационарное решение (19) отвечает геострофическому течению с нулевой потенциальной завихренностью. В данном разделе построен аналог этого решения в рамках полной (точной) негеострофической модели. Как и решение (19), точное решение описывает верхнетропосферную струю, скорость которой обращается в ноль на нижней границе. Принципиально новые особенности связаны с горизонтальной асимметрией струи и формированием разрывов (фронтов) для достаточно больших амплитуд распределений плавучести. Анализ этих особенностей следует работам автора [18, 19], посвященным нелинейной теории геострофического приспособления.
В негеострофической модели рассматривается полная система уравнений динамики стратифицированной вращающейся жидкости, записанная в приближении Буссинеска [1, 3, 19]. Из этой системы следует лагранжев закон сохранения потенциальной завихренности
(39)
${{d\Omega } \mathord{\left/ {\vphantom {{d\Omega } {dt}}} \right. \kern-0em} {dt}} = 0,\,\,\,\,\Omega = \left( {{\text{rot}}{\mathbf{u}} + f{\mathbf{k}},\nabla \sigma } \right),$Для движений, не зависящих от зональной координаты $х$ (двумерных или зональных движений), выражение для $\Omega $ можно представить в виде
где $m$ – так называемый геострофический момент и квадратными скобками обозначен якобиан по переменным $y,z$. В случае стационарных движений, распределения $m,\sigma $ связаны соотношением $f{{m}_{z}} = {{\sigma }_{y}}$, следующим из уравнения термического ветра.Будем рассматривать стационарные двумерные движения с $\Omega = {\text{const}}$ и удовлетворяющие условиям ${\mathbf{u}} \to {\mathbf{0}}$, $\sigma \to {{N}^{2}}z$ при $\left| y \right| \to \infty $. При этом $\Omega = f{{N}^{2}}.$ Примем в качестве масштабов $z,\,y,\,m,\,\sigma $ соответственно $H,\,D,\,D,\,{{N}^{2}}H$, где $D = {{NH} \mathord{\left/ {\vphantom {{NH} f}} \right. \kern-0em} f}$ (радиус деформации), $H$ толщина слоя атмосферы. Тогда, для определения двумерных движений с однородно распределенной ПЗ получим замкнутую систему нелинейных уравнений
(41)
${{m}_{z}} = {{\sigma }_{y}},\,\,\,\,\left[ {m,\sigma } \right] \equiv \frac{{\partial (m,\sigma )}}{{\partial (y,z)}} = 1.$Если в качестве масштаба скорости $u$ принять ${{U}_{0}} = Df,$ то $m = y - u$.
Переходом от независимых переменных $y,\,z$ к переменным $m,\,z$ (аналог преобразования Лежандра) нелинейная система (41) сводится к линейной системе Коши–Римана ${{\sigma }_{z}} = {{y}_{m}}$, ${{\sigma }_{m}} = - {{y}_{z}}$. Из этой системы следует, что $y,\,\sigma $ являются гармоническими функциями переменных $m,\,z$: ${{y}_{{zz}}} + {{y}_{{mm}}} = 0$, ${{\sigma }_{{zz}}} + {{\sigma }_{{mm}}} = 0$. С учетом $y = m + u$, скорость $u = u(m,z)$ также является гармонической функцией. Для однозначного определения этой функции будем считать, что на нижней границе скорость обращается в ноль (за счет действия экмановского трения). Кроме того, будем считать, что на верхней границе задано распределение плавучести $\sigma = \sigma (m)$. Тогда, с учетом уравнения термического ветра, для определения скорости получим смешанную краевую задачу
(42)
${{u}_{{zz}}} + {{u}_{{mm}}} = 0,\,\,\,\,u(m,0) = 0,\,\,\,\,{{u}_{z}}(m,1) = - \sigma {\kern 1pt} '(m),$(43)
$u = u(m,z) = \frac{{a\sin ({{\pi z} \mathord{\left/ {\vphantom {{\pi z} 2}} \right. \kern-0em} 2})}}{{\operatorname{ch} ({{\pi m} \mathord{\left/ {\vphantom {{\pi m} 2}} \right. \kern-0em} 2}) + \cos ({{\pi z} \mathord{\left/ {\vphantom {{\pi z} 2}} \right. \kern-0em} 2})}}.$Для перехода на плоскость физических переменных $(y,z)$ к решению (43) нужно добавить соотношение $y = m + u(m,z)$. При фиксированном значении $z$, выражения $u = u(m,z)$, $y = m + u(m,z)$ дают параметрическое (с параметром $m$) представление функции $u = u(y)$. Формально математически геострофическому решению (19) отвечает предельный случай малых амплитуд $a \ll 1$, когда $y\sim m$. Отметим, что полагая в правой части (43) $m = y - u$, получим уравнение, определяющее функцию $u = u(m,z)$ в неявном виде.
Важная особенность нелинейного решения связана с формированием разрывов. В качестве примера рассмотрим распределение скорости на верхней границе, которое описывается параметрическими соотношениями
(44)
$u = {a \mathord{\left/ {\vphantom {a {\operatorname{ch} }}} \right. \kern-0em} {\operatorname{ch} }}({{\pi m} \mathord{\left/ {\vphantom {{\pi m} 2}} \right. \kern-0em} 2}),\,\,\,\,y = m + {a \mathord{\left/ {\vphantom {a {\operatorname{ch} }}} \right. \kern-0em} {\operatorname{ch} }}({{\pi m} \mathord{\left/ {\vphantom {{\pi m} 2}} \right. \kern-0em} 2}).$Изображая отвечающие (44) зависимости $u = u(y)$ для последовательно возрастающих значений $a$ (рис. 4), можно установить, что при некоторой критической амплитуде $a = {{a}_{{cr}}}$ в распределении $u = u(y)$ формируется разрыв, расположенный при  $y = {{y}_{{cr}}}.$ Возникновение разрыва связано с появлением точки перегиба ${{m}_{{cr}}}$ с горизонтальной касательной на графике функции $y = y(m)$. В этой точке выполняются условия ${{y}_{m}} = {{y}_{{mm}}} = 0$. Из второго условия следует $\operatorname{ch} (\pi {{m}_{{cr}}}) = 3$ или ${{m}_{{cr}}} = {{\pi }^{{ - 1}}}\ln (3 + 2\sqrt 2 ) = 0.561$. Из первого условия находится критическая амплитуда ${{a}_{{cr}}} = {4 \mathord{\left/ {\vphantom {4 \pi }} \right. \kern-0em} \pi } = 1.273$. Сам разрыв формируется в точке ${{y}_{{cr}}} = {{m}_{{cr}}} + {{{{a}_{{cr}}}} \mathord{\left/ {\vphantom {{{{a}_{{cr}}}} {\operatorname{ch} }}} \right. \kern-0em} {\operatorname{ch} }}({{\pi {{m}_{{cr}}}} \mathord{\left/ {\vphantom {{\pi {{m}_{{cr}}}} 2}} \right. \kern-0em} 2}) = 1.834$. Аналогичным образом находятся критические значения параметров для каждого уровня
$z$. Можно показать, что с ростом амплитуды разрывы впервые возникают на верхней границе
(тропопаузе).
$y = {{y}_{{cr}}}.$ Возникновение разрыва связано с появлением точки перегиба ${{m}_{{cr}}}$ с горизонтальной касательной на графике функции $y = y(m)$. В этой точке выполняются условия ${{y}_{m}} = {{y}_{{mm}}} = 0$. Из второго условия следует $\operatorname{ch} (\pi {{m}_{{cr}}}) = 3$ или ${{m}_{{cr}}} = {{\pi }^{{ - 1}}}\ln (3 + 2\sqrt 2 ) = 0.561$. Из первого условия находится критическая амплитуда ${{a}_{{cr}}} = {4 \mathord{\left/ {\vphantom {4 \pi }} \right. \kern-0em} \pi } = 1.273$. Сам разрыв формируется в точке ${{y}_{{cr}}} = {{m}_{{cr}}} + {{{{a}_{{cr}}}} \mathord{\left/ {\vphantom {{{{a}_{{cr}}}} {\operatorname{ch} }}} \right. \kern-0em} {\operatorname{ch} }}({{\pi {{m}_{{cr}}}} \mathord{\left/ {\vphantom {{\pi {{m}_{{cr}}}} 2}} \right. \kern-0em} 2}) = 1.834$. Аналогичным образом находятся критические значения параметров для каждого уровня
$z$. Можно показать, что с ростом амплитуды разрывы впервые возникают на верхней границе
(тропопаузе).
Рис. 4.
Горизонтальные профили скорости (44) на верхней границе для значений амплитуд $a = 0.5$ и $a = {{a}_{{cr}}} = {4 \mathord{\left/ {\vphantom {4 \pi }} \right. \kern-0em} \pi }$.
Картина изолиний поля скорости $u = u(m,z)$ для критической амплитуды $a = {{a}_{{cr}}}$ приведена на рис. 5. Точка сгущения изолиний на рисунке отмечает положение формирующегося разрыва. Представленная картина описывает нелинейный аналог верхнетропосферного струйного течения. Обратим внимание на горизонтальную асимметрию профиля скорости струи – на каждом уровне сдвиг скорости в северной (циклонической) части струи больше чем сдвиг скорости в южной части. Данная особенность, хорошо выраженная в данных наблюдений, анализировалась в работах [10, 11].
Рис. 5.
Изолинии поля $\bar {u} = {u \mathord{\left/ {\vphantom {u a}} \right. \kern-0em} a}$ (43) в плоскости $(y,z)$ для значений $0 < \bar {u} < 1$ с шагом $0.1$.

Завершим данный раздел двумя замечаниями. Первое замечание касается закона сохранения ПЗ в квазигеострофической теории. Выражение для $\Omega $(39) можно записать в виде $\Omega = \left[ {\sigma ,u} \right] + f{{\sigma }_{z}}.$ Полагая $\sigma = {{N}^{2}}z + \sigma {\kern 1pt} '$ и используя квазигеострофические соотношения $fu = - {{\psi }_{y}}$, $\sigma {\kern 1pt} ' = {{\psi }_{z}}$, это выражение преобразуется к виду $\Omega = {{N}^{2}}f$ + $ + \,\,{{N}^{2}}{{f}^{{ - 1}}}\left( {{{\psi }_{{yy}}} + ({{{{N}^{2}}} \mathord{\left/ {\vphantom {{{{N}^{2}}} {{{f}^{2}}}}} \right. \kern-0em} {{{f}^{2}}}}){{\psi }_{{zz}}}} \right) + {{u}_{z}}\sigma _{z}^{'}$. В квазигеострофической теории пренебрегают последним слагаемым и в качестве сохраняющейся величины берут отклонение от постоянного значения ${{\Omega }_{g}} = q$ = ${{\psi }_{{yy}}} + ({{{{N}^{2}}} \mathord{\left/ {\vphantom {{{{N}^{2}}} {{{f}^{2}}}}} \right. \kern-0em} {{{f}^{2}}}}){{\psi }_{{zz}}}$ или, в безразмерных переменных, $q = {{\psi }_{{yy}}} + {{\psi }_{{zz}}}$ . Квазигеострофическое течение с нулевой ПЗ ${{\Omega }_{g}} = 0$, таким образом, отвечает негестрофическому течению с однородно распределенной ПЗ.
Второе замечание касается многозначного решения (43) для закритических значений амплитуд $a > {{a}_{{cr}}}$. Как и в теории нелинейного геострофического приспособления многозначное решение преобразуется в однозначное путем построения поверхности разрыва $y = {{y}_{f}}(z)$. Это осуществляется с использованием непрерывной части решения (43) и “физического” условия непрерывности давления при переходе через разрыв. В терминах $\sigma ,m$ последнее условие дается известной формулой Маргулеса ${{d{{y}_{f}}} \mathord{\left/ {\vphantom {{d{{y}_{f}}} {dz}}} \right. \kern-0em} {dz}}$ = $ - ({{\sigma }_{2}} - {{{{\sigma }_{1}})} \mathord{\left/ {\vphantom {{{{\sigma }_{1}})} {({{m}_{2}}}}} \right. \kern-0em} {({{m}_{2}}}} - {{m}_{1}})$, где ${{\sigma }_{{1,2}}},\,\,{{m}_{{1,2}}}$ – значения переменных по разные стороны от разрыва. Детальное описание алгоритма построения поверхностей разрыва для течений с однородным распределением ПЗ дано в [19]. Использование этого алгоритма показывает, что для струйного течения (43) на небольших расстояниях от верхней границы поверхность разрыва $y = {{y}_{f}}(z)$ представляет собой участок прямой с тангенсом угла наклона к горизонтали порядка ${H \mathord{\left/ {\vphantom {H D}} \right. \kern-0em} D}$.
ЗАКЛЮЧЕНИЕ
В рамках квазигеострофической модели атмосферы с двумя горизонтальными границами (подстилающей поверхностью и тропопаузой) исследовано влияние трения о подстилающую поверхность (экмановского трения) на динамику зональных течений. Предполагается, что течения имеют нулевую ПЗ и вызываются заданными распределениями плавучести на границах. Подробно рассмотрен случай распределений плавучести фронтального типа, индуцирующих систему из двух противоположно направленных струйных течений, расположенных соответственно в верхней и нижней половине слоя атмосферы. Показано, что за счет экмановского трения, осевая скорость нижнего течения падает до нуля, а скорость верхнего течения, постепенно охватывающего всю тропосферу, вырастает в два раза. Таким образом, имеет место эффект усиления или интенсификации скорости течений на верхней границе в присутствии трения.
Следует подчеркнуть, что применительно к реальной атмосфере основным фактором, определяющим интенсивность струйных течений, является перепад температур в системе экватор – полюс. Рассмотренный диссипативный эффект служит дополнительным (и достаточно неожиданным) фактором, способствующим интенсификации течений вблизи верхней границы тропопаузы. Здесь нужно отметить, что в геофизической гидродинамике известны примеры необычных эффектов, связанных с экмановским трением. Так, учет этого трения в моделях бароклинной неустойчивости приводит к исчезновению коротковолнового отсечения – неустойчивыми становятся все нормальные моды [7].
Список литературы
Гилл А. Динамика атмосферы и океана. М.: Мир, 1986. Т. 2. 415 с.
Pedlosky J. Geophysical Fluid Dynamics. Springer-Verlag: Berlin and New York, 1987. 710 p.
Vallis G.K. Atmospheric and Oceanic Fluid Dynamics. Fundamentals and Large-Scale Circulation. Cambridge Univ. Press: Cambridge, 2006. 745 p.
Dolzhansky F.V. Fundamentals of Geophysical Hydrodynamics. Springer-Verlag: Berlin Heidelberg, 2013. 272 p.
Гринспен Х. Теория вращающихся жидкостей. Л.: Гидрометеоиздат, 1975. 304 с.
Должанский Ф.В., Крымов В.А., Манин Д.Ю. Устойчивость и вихревые структуры квазидвумерных сдвиговых течений // Успехи физ. наук. 1990. Т. 160. Вып. 7. С. 1–47.
Willams G.P., Robinson J. Generalized Eady waves with Ekman pumping // J. Atmos. Sci. 1974. V. 31. P. 1768–1776.
Card P.A., Barcilon A. The Charney stability problem with a lower Ekman layer // J. Atmos. Sci. 1982. V. 39. P. 2128–2137.
Kostrykin S.V., Khapaev A.A., Yakushkin I.G. The influence of nonlinear bottom friction on decay properties of cyclonic and anticyclonic vortical structures in the shallow rotated fluid // J. Fluid. Mech. 2014. V. 753. P. 217–241.
Калашник М.В., Нерушев А.Ф., Ивангородский Р.В. Характерные масштабы и горизонтальная асимметрия струйных течений в атмосфере Земли // Изв. РАН. Физика атмосферы и океана. 2017. Т. 53. № 2. С. 179–187.
Воробьев В.И. Струйные течения в высоких и умеренных широтах. Л.: Гидрометеоиздат, 1960. 234 с.
Held I.M., Pierrehumbert R.T., Garner S.T., Swanson K.L. Surface quasigeostrophic dynamics // J. Fluid. Mech. 1995. V. 282. P. 1–20.
Badin G. Surface semi-geostrophic dynamics in the ocean // Geophys. Astrophys. Fluid Dyn. 2013. V. 107. P. 526–540.
Kalashnik M.V., Kurgansky M.V., Kostrykin S.V. Instability of Surface Quasigeostrophic Spatially Periodic Flows // J. Atmos. Sci. 2020. V. 77. P. 239–255.
Калашник М.В., Чхетиани О.Г. О нелинейном затухании вихревых течений во вращающейся жидкости // Докл. РАН. 2014. Т. 456. № 6. С. 717–722.
Незлин М.В., Снежкин Е.Н. Вихри Россби и спиральные структуры. М.: Наука, 1990. 238 с.
Алгазин О.Д., Копаев А.В. Решение смешанной краевой задачи для уравнения Лапласа в многомерном слое // Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015 . № 1. С. 3–13.
Калашник М.В. Формирование фронтов и струйных течений при геострофическом приспособлении в стратифицированной вращающейся жидкости // Докл. РАН. 1997. Т. 357. №2 . С. 247–251.
Kalashnick M.V. Geostrophic adjustment and frontogenesis in the continuously stratified fluid // Dynamics of Atmospheres and Oceans. 2004. V. 38. № 1. P. 1–37.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Физика атмосферы и океана



