Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 6, стр. 669-675

1. ВВЕДЕНИЕ

Обобщенное уравнение эволюции завихренности для баротропной модели вязкой жидкости включает члены линейного и эффективного нелинейного трения, связанные с влиянием на потоки в атмосфере или океане вращения и трения в пограничном слое (ПС) у подстилающей поверхности [1, 2]. Влиянием нелинейного трения объясняется явление циклон-антициклонной асимметрии, наблюдаемой в вихревой структуре атмосферы и океана [2–5]. В [6] это уравнение использовано в численных экспериментах для демонстрации влияния нелинейного трения на процесс слияния мезомасштабных вихрей, образующихся при распаде кольцевого вихря вследствие баротропной неустойчивости.

В [7] это уравнение обобщается на случай горизонтально неоднородного ПС, в котором его основные характеристики и интегральные параметры зависят от горизонтальных координат. В общем случае параметры ПС зависят от скорости потока или его завихренности, а модель экмановского слоя становится нелинейной. В работе [7] для иллюстрации эффектов пространственной изменчивости ПС на эволюцию вихрей в численных экспериментах использована простая зависимость вязкости жидкости k (точнее ее турбулентного аналога), которая входит в определение экмановского масштаба ${{h}_{e}} = \sqrt {{{2k} \mathord{\left/ {\vphantom {{2k} f}} \right. \kern-0em} f}} $, где f – параметр Кориолиса, от скорости потока. Еще одна достаточно простая нелинейная модель может быть получена заменой параметра Кориолиса f на абсолютную завихренность ${{\omega }_{a}} = f + \omega $ и использованием для масштаба Экмана формулы ${{h}_{{e\omega }}} = \sqrt {{{2k} \mathord{\left/ {\vphantom {{2k} {\left( {f + \omega } \right)}}} \right. \kern-0em} {\left( {f + \omega } \right)}}} ,$ где $\omega = {{\partial v} \mathord{\left/ {\vphantom {{\partial v} \partial }} \right. \kern-0em} \partial }x - {{\partial u} \mathord{\left/ {\vphantom {{\partial u} \partial }} \right. \kern-0em} \partial }y$ – относительная завихренность, u и v – компоненты скорости потока вдоль осей х и у [8–10]. Таким образом, горизонтальная изменчивость ПС в такой нелинейной модели ПС в достаточно интенсивных вихрях будет проявляться через поля $\omega = \omega (x,y)$ и ${{h}_{{e\omega }}} = {{h}_{{e\omega }}}(x,y)$. Однако, в общем случае область применения такой модели будет существенно ограничена нереально большими значениями экмановского масштаба ${{h}_{{e\omega }}}$ и условием $\left| {f + \omega } \right| \ne 0$.

В настоящей работе на основе полуэмпирических соображений предлагаются простые приближения для экмановского масштаба, устраняющие его неограниченный рост при стремлении абсолютной завихренности к нулю, но сохраняющие эффект уменьшения толщины ПС под влиянием вращения. Эти приближения использованы для расчета интегральных параметров ПС и их пространственного распределения в обобщенном уравнении завихренности. В численных экспериментах с моделью взаимодействия двух баротропных атмосферных вихрей демонстрируется влияние параметров нелинейной модели ПС на эволюцию поля завихренности.

2. ОБОБЩЕННОЕ УРАВНЕНИЕ ЗАВИХРЕННОСТИ

В работе [7] выведено баротропное уравнение эволюции завихренности ω в слое жидкости глубиной H, в котором горизонтальная изменчивость ПС учитывается через зависимость его интегральных параметров α и β от пространственных координат:

где ψ – функция тока, $J\left( {\psi ,\omega } \right) = {{\psi }_{x}}{{\omega }_{y}} - {{\psi }_{y}}{{\omega }_{x}}$ – якобиан, $\nabla \equiv ({\partial \mathord{\left/ {\vphantom {\partial \partial }} \right. \kern-0em} \partial }x,{\partial \mathord{\left/ {\vphantom {\partial \partial }} \right. \kern-0em} \partial }y)$ – оператор градиента,

τ₀– вектор напряжения трения на подстилающей поверхности, $R\left( V \right) \equiv {{v}_{x}} - {{u}_{y}}$ оператор ротора, действующего на вектор V с компонентами u и v по осям х и у. Интегральные параметры α и β определяются функциями ${{\varphi }_{1}}\left( {\xi ,h} \right)$ и ${{\varphi }_{2}}\left( {\xi ,h} \right)$ (профильными) для вертикального профиля компонент скорости классического экмановского решения [1, 7]: $\alpha \left( h \right) = \left\langle {\operatorname{Re} \left( {\varphi {{{(\xi ,h)}}^{2}}} \right)} \right\rangle $ и β(h) = $ - \left\langle {\operatorname{Im} \left( {\varphi {{{(\xi ,h)}}^{2}}} \right)} \right\rangle $, где $\varphi \left( {\xi ,h} \right)$ = $ - \frac{{{\text{sh}}\left( {\lambda h} \right) - \left( {\lambda h} \right){\text{ch}}\left( {\lambda \left( {\xi - h} \right)} \right)}}{{{\text{sh}}\left( {\lambda h} \right) - \left( {\lambda h} \right){\text{ch}}\left( {\lambda h} \right)}}$ = φ₁(ξ, h) + + iφ₂(ξ, h), $h(x,y) = {H \mathord{\left/ {\vphantom {H {{{h}_{{e\omega }}}}}} \right. \kern-0em} {{{h}_{{e\omega }}}}}(x,y)$, $\xi = {z \mathord{\left/ {\vphantom {z {{{h}_{e}}}}} \right. \kern-0em} {{{h}_{e}}}}$ – безразмерная вертикальная координата, $\lambda = 1 + i$, $\left\langle {} \right\rangle $ – символ интегрирования по вертикальной координате $\xi $. Для простейшей линейной модели вязкого экмановского ПС эти параметры α и β постоянны и два первых члена в правой части (1) исчезают. В таком варианте уравнение (1) в [1] названо обобщенным уравнением эволюции завихренности, в котором третий член в левой части с коэффициентом α представляет инерционную нелинейность, связанную с экмановским слоем, а член с коэффициентом β – нелинейную часть эффективного трения. Как показано в [7], первый член в правой части (1) можно интерпретировать как орографический (топографический) эффект ПС, поскольку горизонтальные градиенты параметров α и β определяются градиентами масштаба толщины ПС. Второй член Ф зависит от вторых пространственных производных параметров α и β, при достаточно большой их изменчивости (вследствие изменчивости ${{h}_{{e\omega }}} = {{h}_{{e\omega }}}(x,y)$) может быть источником интенсивных мелкомасштабных возмущений поля вихря. Все перечисленные члены, представляющие нелинейное трение в уравнении (1), следуют из нелинейности исходных уравнений движения при интегрировании по вертикали вторых моментов в уравнении вихря, которые появляются при представлении скорости суммой средней по вертикали и зависящих от вертикальной координаты компонент экмановского потока в ПС [1].

Функции $\alpha \left( h \right)$ и $\beta \left( h \right)$ и их горизонтальная изменчивость определяются видом профильных функций и в общем случае зависят от принятой модели ПС. Для упрощения выкладок и окончательных выражений мы далее используем точные решения, выписанные выше, но в них масштаб высоты ПС полагается функцией от абсолютной завихренности.

3. УРАВНЕНИЕ ДЛЯ ЭКМАНОВСКОГО МАСШТАБА

В классической краевой линейной задаче Экмана для горизонтально однородных течений вязкой жидкости над подстилающей поверхностью на вращающейся Земле выделяется характерный масштаб ${{h}_{e}} = \sqrt {{{2k} \mathord{\left/ {\vphantom {{2k} f}} \right. \kern-0em} f}} ,$ который используется для нормировки вертикальной координаты в известных точных решениях задачи. Масштаб h_e качественно правильно учитывает влияние вращения на высоту области наиболее значительных изменений в вертикальных профилях компонент скорости потоков у поверхности, но нереально возрастает при $f \to 0$. Попытки учета горизонтальной неоднородности потоков приводят к нелинейным задачам, точное решение которых получить невозможно, а приближенные решения обычно ищутся только для малых чисел Россби $r = {\omega \mathord{\left/ {\vphantom {\omega f}} \right. \kern-0em} f} \ll 1$ [10]. Однако в реальных атмосферных вихрях типа тропических циклонов число Россби может превышать 10. Поэтому мы, упрощая модель ПС, для расчета интегральных параметров $\alpha \left( h \right)$ и $\beta \left( h \right)$ в обобщенном уравнении вихря будем использовать известные точные решения задачи Экмана [1], выписанные выше, с масштабом толщины ${{h}_{{e\omega }}} = \sqrt {{{2k} \mathord{\left/ {\vphantom {{2k} {\left( {f + \omega } \right)}}} \right. \kern-0em} {\left( {f + \omega } \right)}}} $ = ${{h}_{e}}\sqrt {{1 \mathord{\left/ {\vphantom {1 {(1 + r)}}} \right. \kern-0em} {(1 + r)}}} $.

Далее мы модифицируем соотношение h_eω = = ${{h}_{e}} \cdot \sqrt {{1 \mathord{\left/ {\vphantom {1 {(1 + r)}}} \right. \kern-0em} {(1 + r)}}} $ таким образом, чтобы оно давало ограниченные значения ${{h}_{{e\omega }}}$ при любых значениях числа Россби r, сохраняя при этом эффект уменьшения масштаба толщины ПС при увеличении относительной завихренности (при увеличении r) вне зависимости от ее знака. Здесь мы руководствуемся практическими соображениями гладкого сопряжения режимов с малыми и большими r, аналогичных тем, которые используются в [11] при выводе полуэмпирических формул для характерных масштабов, объединяющих различные режимы ПС. Так, предполагая, что реальные масштабы пограничного слоя h ограничены некоторой заданной высотой H (например, высотой однородной атмосферы), мы определим новый масштаб ПС h соотношением ${{h}^{{ - 1}}} = h_{{ew}}^{{ - 1}} + {{H}^{{ - 1}}}$. Для безразмерного масштаба, нормированного на обычный масштаб Экмана ${{h}_{e}} = \sqrt {{{2k} \mathord{\left/ {\vphantom {{2k} f}} \right. \kern-0em} f}} $, получаем

где введена безразмерная предельная высота $H* = {H \mathord{\left/ {\vphantom {H {{{h}_{e}}}}} \right. \kern-0em} {{{h}_{e}}}} = {{\varepsilon }^{{ - 2}}}$, $\varepsilon = {{(H*)}^{{ - 2}}}$ – число Экмана. Далее аппроксимируем эту функцию при малых r такой ограниченной функцией, которая исключает разрыв производной по r при r = –1. Для этого используем простейшую рациональную функцию, удовлетворяющую указанным требованиям:

Здесь коэффициенты а₀, а₁, а₂ вычисляются методом наименьших квадратов для отклонений $h{\text{*}}(r,H*,\vec {a})$ от $h{\text{*}}(r)$ для заданного значения параметра H*. Для используемых далее в численных экспериментах значений H* а₀, а₁, а₂ даются в табл. 1. На рис. 1 показан вид функции $h{\text{*}}(r,H*,\vec {a})$ для H* = 8.

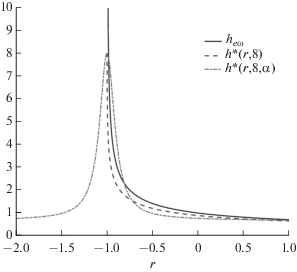
Таким образом, соотношение (2) дает нам полуэмпирическую нелинейную модель экмановского ПС, в которой вертикальный масштаб определяется двумя внешними параметрами: числом Россби r и безразмерной высотой H* (или числом Экмана $\varepsilon = {{({{H}^{ * }})}^{{ - 2}}}$). Выбор значения H* определяет диапазон изменчивости h* и, как следствие, диапазон значений интегральных параметров α и β в уравнении завихренности (1). Такая изменчивость α и β может оказывать значительное влияние на эволюцию поля завихренности, учитывая наличие вторых пространственных производных в члене Ф в правой части (1), что будет далее показано в численных экспериментах с моделью взаимодействия двух баротропных вихрей.

В численных экспериментах, так же как и в [7], в расчетах для параметров α(h) и β(h) были использованы простые рациональные функции, аппроксимирующие сложные аналитические выражения для них в диапазоне характерных для атмосферы значений параметра h:

где $\vec {a} = ( - 0.304;0.091; - 0.271;$ $6.485 \times {{10}^{{ - 3}}};0.058)$ и α^max = 0.197, $\vec {b}$ = (–0.489; 0.692; –0.501; 0.245) и b^max = 0.08. Эти функции достаточно точно аппроксимируют профильные функции α(h) и β(h), являются гладкими и положительными для диапазона используемых значений h.

4. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Влияние предложенной нелинейной модели экмановского пограничного слоя на динамику вихревых образований демонстрируется в численных экспериментах на примере задачи о взаимодействии пары идентичных баротропных атмосферных вихрей типа тропических циклонов. Даже в простейших постановках таких задач для идеальной жидкости можно видеть большое разнообразие эволюции вихрей в зависимости от расстояния между ними, их размерами и соотношения интенсивностей [12]. Ставить и решать более реалистичные задачи взаимодействия атмосферных и океанских вихрей, оставаясь в рамках квазидвумерных численных моделей, позволяют модели вязкой жидкости, включающие члены нелинейного трения в ПС в уравнении завихренности (1) с использованием при этом нелинейной модели экмановского ПС, описанной выше.

Во всех численных экспериментах начальное поле завихренности задавалось в квадратной области [1600 × 1600 км] в виде суммы завихренности двух одинаковых вихрей, с центрами на оси х, расположенных симметрично относительно центра области на расстоянии 300 км. Завихренность в вихрях задается функцией расстояния r от их центра [7, 13]:

где V_m – максимум тангенциальной составляющей скорости ветра, r_m – радиус максимального ветра, b – параметр, определяющий изменение тангенциальной составляющей скорости ветра вдоль радиуса. В экспериментах приняты значения b = 1.5, V_m = 15 м/с, r_m = 100 км, характерные для атмосферных мезомасштабных вихрей в тропиках типа тропических циклонов. Начальное поле завихренности показано на рис. 2.

Уравнение (1) решалось псевдоспектральным методом на равномерной сетке с числом узлов 256 × × 256 с двойными периодическими граничными условиями. Интегрирование по времени на срок 5 суток проводилось методом Адамса–Бэшфорта второго порядка. Для ограничения роста возмущений малых масштабов, приводящего к неустойчивости счета, в пространстве волновых чисел применялся фильтр [14]:

где K – волновое число, K₀ – волновое число среза фильтра, α и M – параметры, определяющие степень подавления компонент с волновыми числами более K₀. В расчетах использовались следующие значения: α =18.4, M = 4 и K₀= 2/3. Данный фильтр применялся к полю завихренности на каждом шаге интегрирования по времени. В процессе проведения численных экспериментов наблюдалась численная неустойчивость, связанная с большой пространственной изменчивостью $h{\text{*}}(x,y)$, и, как следствие, с высокой изменчивостью члена Ф в (1). Для подавления этой неустойчивости к полям $h{\text{*}}(x,y)$ и Ф(x, y) на каждом шаге интегрирования применялся простой фильтр скользящего среднего с окном размером 5 × 5. В дополнение к экмановскому трению на подстилающей поверхности учитывалось квадратичное трение с помощью аэродинамической формулы ${{\tau }_{{CD}}} = \rho {{С}_{D}}\left| V \right|V$, где ${{C}_{D}} = {{C}_{0}} + {{C}_{V}}\left| V \right|,$ С₀ = 10^–3, С_V = 10^–4 [7], которое служит еще одним механизмом подавления вычислительной неустойчивости.

Для иллюстрации влияния нелинейной модели пограничного слоя и дополнительных нелинейных членов в (1), учитывающих горизонтальную неоднородность его интегральных характеристик, на эволюцию поля завихренности пары вихрей были проведены эксперименты с f = 5 × × 10^–5 c^–1 и Н = 10 км со следующими наборами параметров:

1) постоянные параметры α и β, соответствующие h_e ~ 600 м;

2) модель с масштабом $h{\text{*}}(r,H*,\vec {a})$ для H* = 8, $\Phi = 0$;

3) три эксперимента с масштабом $h{\text{*}}(r,H*,\vec {a})$ для H* = 2, 5 и 8.

Последние три эксперимента демонстрируют влияние нелинейного члена Ф в уравнении (1) в зависимости от предельной высоты пограничного слоя.

Результаты всех пяти экспериментов в виде полей завихренности в разные моменты времени представлены на рис. 3.

В течение первых суток во всех экспериментах наблюдается эффект взаимного притяжения циклонических ядер вихрей и их циклоническое вращение относительно друг друга (эффект Фудзивары [15]). На вторые сутки области с отрицательной завихренностью обоих вихрей сворачиваются в отдельные антициклонические вихри-сателлиты. Циклонические области в первом и во втором экспериментах продолжают сближаться (практически сливаются) и образуется триполярная структура – циклон и два антициклона.

Поля завихренности, полученные в первом и во втором экспериментах, мало отличаются от таковых на рис. 1 в [7], где наблюдается слияние пары баротропных вихрей и образования триполярной структуры. Некоторые отличия могут быть связаны, прежде всего, с различиями в аппроксимирующих функциях для α(h) и β(h) и методах численного решения уравнения (1) здесь и в [7].

Эффект включения члена Ф четко проявляется в экспериментах для всех используемых значений H*, циклонические области после сближения в первые сутки начинают расходиться. В районах антициклонической завихренности развиваются мезо- и мелкомасштабные вихри и филаменты, в экспериментах для H* = 5 и H* = 8 становится заметной асимметрия. Отметим, что влияние члена Ф на структуру полей в [7] оказалось незначительным, что связано с введением сравнительно слабой изменчивости ПС через коэффициент турбулентной вязкости в экмановском масштабе h_e, который связывался с модулем скорости потока квадратичной зависимостью.

В последующие двое суток влияние члена Ф проявляется еще более четко. Тогда как в первых двух экспериментах без члена Ф в центре произошло слияние циклонов, в экспериментах с Ф они расходятся и при H* = 8 видим уже два циклона на значительном расстоянии друг от друга. При этом заметно увеличивается число и интенсивности мелкомасштабных структур. В антициклонических областях наблюдается асимметрия, более заметная при бόльших H*.

Скорость разбегания циклонических вихрей зависит от величины H* – при малых значениях они расходятся медленнее. Изменения расстояния между центральной парой циклонических вихрей для серии расчетов третьего эксперимента представлены в табл. 2.

В первые сутки вихри сближаются на одинаковое расстояние независимо от значения H*, затем начинают разбегаться. Так, для H* = 8 расстояние между центрами вихрей к пятым суткам увеличилась более чем в два раза от начального (300 км) и составила около 680 км. Для H* = 5 расстояние между циклонами увеличилось до 500 км. В эксперименте для H* = 2 увеличение расстояния между парой вихрей продолжается до четвертых суток интегрирования и достигает 390 км, а затем к концу пятых суток циклоны начали сближаться до 350 км.

Появление мелкомасштабных структур при включении члена Ф можно интерпретировать как проявление специфического механизма генерации квазидвумерной турбулентности, отличного от известных механизмов баротропной неустойчивости квазидвумерных потоков. Он связан с сильной нелинейностью использованной модели планетарного ПС и, как следствие, значительной пространственной изменчивостью его интегральных характеристик α(h) и β(h) и с наличием вторых пространственных производных в члене нелинейного трения Ф. На реалистичность таких мелкомасштабных структур в нашей модели указывает то, что общая картина мелких вихрей и филаментов в экспериментах при H*= 8 подобна мелким структурам в полях завихренности моделируемого тропического циклона, полученных в численных экспериментах с региональной моделью высокого разрешения [16].

5. ЗАКЛЮЧЕНИЕ

В данной работе предложена простая полуэмпирическая нелинейная модель экмановского пограничного слоя, устраняющая его неограниченный рост при стремлении параметра Кориолиса f или абсолютной завихренности ω_a к нулю. Эта модель использована в обобщенном уравнении завихренности для модели взаимодействия пары вихрей. Численные эксперименты показывают, что включение такой модели в обобщенное уравнение завихренности приводит к ряду новых качественных эффектов в эволюции полей завихренности: генерация интенсивных мелкомасштабных структур и увеличение расстояния между вихрями вместо их слияния. Такие эффекты в значительной степени зависят от безразмерных чисел Россби и Экмана, поэтому необходимо более детальное исследование их влияния на эволюцию полей завихренности в задачах взаимодействия баротропных вихрей.

Работа выполнена в рамках госзадания ТОИ ДВО РАН тема № 0271-2019-0011 (рег. номер АААА-А17-117030110037-8) при финансовой поддержке РФФИ по проектам № 18-05-80011 и № 19-55-10001.