Известия РАН. Физика атмосферы и океана, 2021, T. 57, № 6, стр. 721-732

2.1. Лагранжевые инварианты и условия выполнения закона сохранения PV

Пусть переменная $q(x,y,z,t)$ является лагранжевым инвариантом, что означает, что физическая величина $q(x,y,z,t)$ сохраняется для жидкой частицы во время ее движения, где x и y – горизонтальные переменные, z – вертикальная, t – время; система координат правая.

Согласно теореме Эртеля, величина

является лагранжевым инвариантом. Величину $\Omega {\text{*}}$, рассчитываемую по формуле (1), назовем “потенциальной завихренностью в широком смысле”. Здесь функция $\eta (x,y,z,t)$ – также некий лагранжевый инвариант, ${\mathbf{\Omega }} = {\text{rot}}\,{\mathbf{U}}$ – ротор скорости потока, ${\mathbf{\omega }}$ – угловая скорость вращения Земли, $\rho (x,y,z,t)$ – плотность воды. Условия, при которых ${{\Omega }_{*}}$ является лагранжевым инвариантом следующие:

1. Жидкость идеальная (вязкость отсутствует);

2. Массовые силы потенциальны ${\text{rot}}\,{\mathbf{F}} = 0$;

3. Характеристика $\eta (x,y,z,t)$$~$является лагранжевым инвариантом;

4. Характеристика $\eta (x,y,z,t) = \eta (\rho ,P)$ зависит от плотности $\rho $ и давления P.

Нарушение этих условий приводит к тому, что $\Omega {\text{*}}$ перестанет сохраняться для жидкой частицы и уже не будет являться лагранжевым инвариантом. Часть этих условий можно принять, как, например, условие 2. Условие 1 считается справедливым для очень многих типов движения геофизической гидродинамике, в том числе для мезомасштабных явлений. Однако это условие нарушается в тонких придонных и приповерхностных экмановских слоях. Условие 3 самое расплывчатое: можно в качестве $\eta $ взять энтропию, как часто делают в физике атмосферы, но тогда рассматриваются только адиабатические процессы. Но для океана в этом случае возникает проблема со свойством 4, где энтропия зависит не только от $\rho $ и давления P, но также от солености и температуры. Однако в этом случае можно использовать другие лагранжевы инварианты, например, потенциальную плотность или потенциальную температуру, которые обладают нужными свойствами. Эртель для океана предложил в качестве функции $\eta (x,y,z,t)$ использовать плотность $\rho $ с дополнительным условием несжимаемости:

Далее мы будем использовать выражение “потенциальная завихренность” в терминах соотношения (2), введя для него специальное обозначение PV:

Условия, при которых PV по формуле (3) является лагранжевым инвариантом, следующие:

a) жидкость идеальная (вязкость отсутствует);

b) массовые силы потенциальны ${\text{rot}}\,{\mathbf{F}} = 0$;

c) жидкость несжимаемая;

d) диффузия плотности отсутствует.

Нарушение перечисленных требований приводит к тому, что рассчитываемое по формуле (3) PV для жидких частиц не сохраняется и, следовательно, не может являться лагранжевым инвариантом [13].

С точки зрения физики потенциальная завихренность PV представляет собой лагранжев инвариант, объединяющий свойства – вращение жидкой частицы и деформацию ее формы. В геометрическом смысле это скалярное произведение векторов полного вихря и градиента логарифма плотности. Направление градиента плотности, называемое термодинамической вертикалью, слабо отличается от географической вертикали. Это дает возможность совершать различного рода упрощения математических формулировок задач. PV – это кинематическая характеристика движущейся частицы. В общем случае потенциальный вихрь не сохраняется. Однако в каких-то зонах океана это несохранение незначительно или эволюция происходит слишком медленно, так что на характерных рассматриваемых временных масштабах потенциальный вихрь частиц почти сохраняется. В этом случае можно рассматривать модели океана с сохраняющейся потенциальной завихренностью жидких частиц.

В гидродинамике под вихрем мы понимаем вращающуюся жидкость, а в качестве наиболее адекватной кинематической характеристики для описания вихрей считается ротор скорости ${\mathbf{\Omega }} = {\text{rot}}\,{\mathbf{U}}$, т.е. относительная завихренность. Именно по величине ${\mathbf{\Omega }}$ мы судим о том, сильный вихрь или слабый, а по знаку вертикальной компоненты ${\mathbf{\Omega }}$ мы определяем его полярность. Однако исключительно по величине PV мы ничего не можем сказать об интенсивности вихря и даже не можем определить: циклон это или антициклон. Большая величина PV не означает, что здесь присутствует интенсивный вихрь, и, наоборот, малое значение PV не связано со слабым вихрем.

Если PV не характеризует интенсивность вихря, тогда возникает законный вопрос: какая польза от PV? Ответ зависит от ответа еще на один вопрос: является ли PV лагранжевым инвариантом или нет? Если PV – лагранжев инвариант, т.е. сохраняется у движущейся частицы, то, нарисовав изолинии $PV(x,y,z,t)$ (или поверхности равной потенциальной завихренности), мы выделяем области, из которых частица выйти не может. Частицы не пересекают поверхности равных значений потенциальной завихренности $PV(x,y,z,t)$, однако при своем движении частицы могут деформировать и передвигать контуры равной PV. Благодаря изолиниям $PV(x,y,z,t)$ мы можем определить области движения частиц жидкости.

Однако, если PV не лагранжев инвариант, т.е. не сохраняется у движущейся частицы, то, даже рассчитав поля $PV(x,y,z,t)$, мы не сможем найти ограничения на области движения частиц. В этом случае частицы могут пересекать изолинии $PV(x,y,z,t)$. Для частиц во время их перемещений изменяется величина $PV = \frac{{({\mathbf{\Omega }} + 2{\mathbf{\omega }})\nabla \rho }}{\rho }$. Это означает, что у частиц изменяется относительная завихренность ${\mathbf{\Omega }} = {\text{rot}}\,{\mathbf{U}}$ совместно с полем плотности в окружающем частицу пространстве. При этом уменьшение PV не обязательно сопровождается ослаблением вихря.

Таким образом, в общем случае потенциальный вихрь PV не сохраняется в областях океана, где генерируются вихри, как и не сохраняется в зонах, где вихри быстро диссипируют из-за вязкости.

2.2. Подход Эртеля

Основные методы расчета PV опираются на теорему Эртеля, где исходной формулой является соотношение (3). Однако в действительности расчеты по этой формуле практически никто не делает. Дело, по-видимому, в том, что при вычислении $\nabla \rho $ по натурным данным очень неравноценны вертикальная и горизонтальная составляющие и их изменчивость. В вертикальном направлении $\nabla \rho $ сильно изрезан, и часто требуется сглаживание, которое, в свою очередь, нивелирует некоторые движения. Один из вариантов расчета PV предполагает отдельно вычислять вертикальные и горизонтальные составляющие, а именно:

Далее в первом слагаемом формулы (4) делают следующие подстановки: $\frac{1}{\rho }\frac{{\partial \rho }}{{\partial z}} \cong - \frac{1}{g}{{N}^{2}}(z)$, Ω_z = = $\frac{{\partial v}}{{\partial x}} - \frac{{\partial u}}{{\partial y}} = \zeta $, u и v – горизонтальные составляющие вектора скорости ${\mathbf{V}} = \left\{ {u,v,w} \right\}$, 2ω_z = = $f = 2\omega \sin \varphi $, $\omega $ – угловая скорость вращения Земли, N – частота Вяйсяля–Брента, f – параметр Кориолиса, g – ускорение свободного падения, $\varphi $ – широта. Тогда формула (4) переписывается следующим образом:

Многие авторы при расчете PV отбрасывают горизонтальные составляющие формул (4) или (5), считая их малыми по сравнению с первым слагаемым, а также иногда меняют знак PV на противоположный для того, чтобы значения PV были положительными, что позволяет использовать для оценок логарифмическую шкалу. Рассмотрим несколько формул, по которым на практике часто рассчитывается потенциальная завихренность для вихрей.

В работе [17] при расчете PV для Лофотенского вихря авторы отбрасывают второе слагаемое и рассчитывают только вертикальную составляющую потенциальной завихренности q по формуле:

где ${{\rho }_{0}}$ – референтная плотность, относящаяся к поверхности. Изменение знака в формуле (6), очевидно, связано с тем, что расчеты PV по формуле (6) дают отрицательные значения (в северном полушарии), так как $\frac{{\partial \rho }}{{\partial z}} < 0$ (ось z направлена вверх).

В работе [18] потенциальную завихренность для антициклонического вихря, расположенного в желобе Роколл (Rockall Trough), рассчитывают по более полной формуле:

Формула (7) является одной из форм записи формулы (5), где вместо $\rho $ используется ${{\sigma }_{0}}$ – потенциальная плотность, а горизонтальный градиент скорости записывается в виде: Ω_h = = $\left\{ {\frac{{\partial w}}{{\partial y}} - \frac{{\partial v}}{{\partial z}};\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}}} \right\} \approx \left\{ { - \frac{{\partial v}}{{\partial z}};\frac{{\partial u}}{{\partial z}}} \right\}$. Еще одно упрощение в формуле (7), это ${{({\mathbf{\Omega }} + 2{\mathbf{\omega }})}_{h}} \approx {{{\mathbf{\Omega }}}_{h}}$. Обратим внимание, что в формуле (7) оба слагаемых снова взяты с обратным знаком.

Далее, учитывая, что $b = - \frac{{g\rho }}{{{{\rho }_{0}}}}$ – сила плавучести, формулу (5) можно записать в другом виде:

Здесь ${{{\mathbf{\Omega }}}_{h}} = \left\{ {\frac{{\partial w}}{{\partial y}} - \frac{{\partial v}}{{\partial z}};\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}}} \right\}$ – горизонтальные составляющие ротора скорости (горизонтальная завихренность). Если не учитывать вертикальную составляющую скорости w и также пренебречь членом с ${{{\mathbf{\omega }}}_{h}}$ в силу его малости, получим

Тогда формулу (8) можно записать в виде:

Формула (9) чаще всего используется при расчете потенциальной завихренности для вихрей, в частности, в работе [19], где она используется в полярной системе координат $\left( {r,\theta } \right)$:

Здесь ${\mathbf{V}}$ – поле скорости, $b \equiv - g\frac{\rho }{{{{\rho }_{0}}}}$ – ускорение силы плавучести, ${{N}^{2}} \equiv \frac{{\partial b}}{{\partial z}},$ а $\zeta \equiv \frac{1}{r}\frac{{\partial \left( {r{{\theta }_{0}}} \right)}}{{\partial r}}$ – относительная завихренность.

2.3. Недостатки формулы (9)

При замене $\frac{1}{\rho }\frac{{\partial \rho }}{{\partial z}} \cong - \frac{1}{g}{{N}^{2}}(z)$ предполагается, что возмущение частоты Вяйсяля–Брента движением жидкости мало. Но в мезомасштабных вихрях подъем и опускание изопикн в действительности может быть очень большим, особенно в периоды зимней конвекции [20–22]. Поэтому в расчетах частоты Вяйсяля–Брента возможны большие погрешности, которые ведут к погрешности оценок PV по формуле (9).

Кроме того, стандартная частота Вяйсяля–Брента вычисляется в состоянии покоя [23]. При наличии движения она может также зависеть и от пространственных переменных, причем эти изменения могут быть существенными. Однако в формуле (9) все это не учитывается. Таким образом, главная возможная причина отличия соотношений (3) и (9) кроется в именно в частоте Вяйсяля–Брента.

Тогда возникает резонный вопрос: а почему бы сразу не работать с исходной формулой Эртеля (3) и не переходить к другим формам записи? Очевидно, что ответ положительный, и тогда получается выражение для PV, выражающее зависимость непосредственно от градиентов плотности и скоростей течений:

Эту формулу можно немного упростить, если система координат выбрана так, что ось $x$ направлена на восток, ось $y$ – на север, ось $~z$ – вверх. Тогда в северном полушарии $2{\mathbf{\Omega }} = (0,{{f}_{h}},f)$, где ${{f}_{h}} = 2\omega \cos \varphi $. Так как вертикальная составляющая скорости на несколько порядков (как минимум, на три) меньше горизонтальных, то соответствующие производные будут ничтожно малы, и тогда

Отметим, что отклонение от условий (a–d) с учетом возможной дополнительной ошибки при вычислении частоты Вяйсяля–Брента приводит к тому, что на практике PV у частиц не сохраняется.

2.4. PV для периода глубокой конвекции

Обратим внимание, что в соотношениях (5), (9) и (12) для расчетов PV не требуется выполнения условий геострофичности и гидростатичности, вследствие чего эти формулы должны выполняться, вообще говоря, для всех движений, в том числе для вихрей и вихревых нитей. В случае зимней конвекции PV, по-видимому, формируется самой конвекцией, и закон сохранения следует заменить на закон ее эволюции. В реальности вся теория PV строится без учета вязкости и диффузии, а в периоды глубокой конвекции эти эффекты должны быть крайне важны и рассматриваться отдельно.

2.5. Подход Россби: квазигеострофическое приближение

Для квазигеострофического приближения (число Россби Ro < 1) выражение (3) для потенциального вихря Эртеля значительно упрощается. В частности, для мезомасштабных (возможно, также и субмезомасштабных) явлений, потенциальный вихрь можно представить в виде функции $\sigma $ в приближении f-плоскости:

где $\psi $ – функция тока. Иногда вместо (13) рассматривают $\sigma $ на $\beta $-плоскости:

Выражения (13) и (14) для потенциального вихря отличаются по размерности от PV, рассчитываемой по формулам (3), (5) и (9) с точностью до постоянного размерного множителя. В (13) и (14) размерность $\sigma $ совпадает с размерностью относительной завихренности, и такой подход улучшает физическое толкование потенциальной завихренности, так как здесь большие по модулю значения $\sigma $ соответствуют мощным вихрям и наоборот. Однако при этом подходе на практике часто возникают проблемы с расчетами частоты Вяйсяля–Брента, которая не должна обращаться в нуль.

Подчеркнем важное математическое свойство потенциального вихря в формулировке Россби – согласно (13), $\sigma $ выражается только через одну функцию тока $\psi .~~$Поэтому соотношение (13) в случае однородной потенциальной завихренности ядра можно рассматривать как постановку задачи о нахождении и эволюции функции тока и границы вихревого ядра. Для эллипсоидальной формы ядер такая задача решается аналитически, и этот подход изложен в работах [24–31]. Аналитические соотношения, полученные в этих работах, можно использовать для качественного и количественного сравнения натурных и теоретических характеристик вихрей.

3.1. Краткая характеристика Лофотенского вихря

Лофотенский вихрь расположен в центральной глубоководной части Лофотенской котловины Норвежского моря (рис. 1). Он был обнаружен в ходе гидрографических исследований Арктического и Антарктического научно-исследовательского института в 1970–1980-х гг. [32, 33]. В настоящее время Лофотенский вихрь представляет собой один из наиболее изученных вихрей в Мировом океане. Его существование подтверждено данными in situ [34], спутниковой альтиметрии [35, 36] и данными моделирования [20, 22]. Авторы [37] указывают положение Лофотенского вихря согласно данным гидродинамического моделирования в области, ограниченной 69°–70° с.ш. и 3°–5° в.д.

Квазипостоянный антициклонический Лофотенский вихрь – это конвективная линза теплой и соленой воды на глубине 200–1000 м с пространственным масштабом, достигающим на поверхности 100 км. На поверхности Лофотенский вихрь проявляется повышенными значениями дисперсии аномалий уровня океана, из-за чего Лофотенскую котловину по праву называют “hot spot” Северной Атлантики [38]. Основной причиной регенерации вихря является осенне-зимняя конвекция [21, 22, 32, 33, 39–42]. Кроме того, Лофотенский вихрь подпитывается мезомасштабными вихрями, отделяющимися от ветвей Норвежского течения [35, 36, 43, 44]. Для Лофотенского вихря характерны значительные орбитальные скорости 0.7–0.8 м с^–1 [19, 43] и незначительный циклонический дрейф в пределах глубоководной части Лофотенской котловины.

3.2. Используемые данные

Для расчетов потенциальной завихренности использовались данные реанализа GLORYS12V1 (Global Ocean Physics Reanalysis), доступные на портале CMEMS (Copernicus Marine Environment Monitoring Service. Продукт GLORYS12V1 – вихреразрешающий реанализ Мирового океана с пространственным разрешением 1/12° на 50 горизонтах для периода, в который имеются альтиметрические наблюдения. Он основан на глобальной системе прогнозирования CMEMS в режиме реального времени. Моделью океанических условий выступает NEMO с форсингом ECMWF ERA-Interim. Наблюдения ассимилируются с помощью фильтра Калмана уменьшенного порядка. Данные спутниковых альтиметров (аномалия уровня моря), температура поверхности моря, концентрация морского льда и вертикальные профили температуры и солености in situ ассимилируются совместно. Данный продукт включает в себя ежедневные трехмерные поля потенциальной температуры, солености и течений, двумерные поля уровня, глубины верхнего квазиоднородного слоя, придонной потенциальной температуры, толщины льда, типов льда, скоростей дрейфа льда. Ассимилированные наблюдения: Reynolds 0.25° AVHRR-only SST, аномалии уровня со всех альтиметров, данные профилей температуры и солености из базы CMEMS CORAv4.1, данные по льду из базы CERSAT Sea Ice oncentration. Граничные условия по температуре и солености на 1991 г. принимались по данным EN.4.2.0. Для расчетов использовались данные GLORYS12V1 за 10 июня 2010 г. Батиметрия ETOPO1, береговая линия GEBCO8.

3.3. Оценки PV для Лофотенского вихря по формуле Эртеля

Для расчетов потенциальной завихренности по формуле Эртеля использовалась формула (12). На первом этапе было проведено сравнение вклада слагаемых этой формулы, которое показало, что основной вклад дает третье слагаемое, в то время как вклад других слагаемых уступает на два порядка (рис. 2). Это означает, что на практике можно не учитывать горизонтальные изменения завихренности и силы Кориолиса, ограничиваясь оценками, которые определяются только вертикальной составляющей. Таким образом, расчеты потенциальной завихренности по Эртелю проводились по следующей формуле:

На рис. 2а и 3 видно, что на графике $PV$ хорошо выделяется ядро Лофотенского вихря, окруженное сгущением изолиний $PV$. Заметим, что во всей исследуемой области $PV < 0$, однако в ядре имеются нулевые значения. Минимальные отрицательные значения PV $ \sim - 1.0 \times {{10}^{{ - 10}}}$ м^–1 с^–1 расположены на периферии ядра, где также наблюдается сгущение изопикн. Отметим, что в областях минимальных значений $PV$ и сгущения изопикн наблюдаются также экстремумы слагаемых, которые обусловлены горизонтальными градиентами относительной завихренности и силы Кориолиса (2б, 2в). На рис. 3 видно, что нулевые значения $PV$ охватывают большую площадь по сравнению с таковыми в распределении завихренности $\zeta $, экстремумы которой локализованы в более узкой области, что проявляется как на вертикальных, так и горизонтальных разрезах. Области положительных значений $\zeta $, соответствующие циклоническому вращению частиц, соответствуют минимальным значениям $PV$ $ \sim - 1.0 \times {{10}^{{ - 10}}}$ м^–1 с^–1. На рис. 3 хорошо видно, что нулевые значения $PV$ выделяют замкнутое ядро в слое 100–800 м, в то время как динамический сигнал в вихре и наличие завихренности прослеживаются до самого дна (3250 м). Это подтверждает, что потенциальная завихренность Эртеля $PV$ не связана ни с интенсивностью вихря, ни с направлением вращения частиц и является кинематической, а не динамической характеристикой вихря.

3.4. Расчет потенциальной завихренности для квазигеострофического приближения на f-плоскости

Расчет $\sigma $ производился по формуле (13) в предположении выполнения гидростатического приближения и малости числа Россби. На рис. 4 показано, что число Россби для Лофотенского вихря не превышает 0.3. Частота Вяйсяля–Брента и функция тока вычислялись с помощью термодинамического уравнения TEOS-10 [23], реализованного в среде Matlab. Для расчетов функции тока применялся алгоритм Каннингема [23, 45]. В следующей статье мы представим оригинальный алгоритм расчета второго слагаемого в формуле (13), который приведет к пересмотру принятого подхода.

На рис. 5 видно, что график $\sigma $ идентичен графику относительной завихренности Ω_z = = $\frac{{\partial v}}{{\partial x}} - \frac{{\partial u}}{{\partial y}} = \zeta $ при данном подходе (рис. 3). Это означает, что изолинии $\sigma $ и $\zeta $ практически совпадают и, следовательно, характеристики $\sigma $ и $\zeta $ в вихревом ядре связаны функциональной зависимостью. Величины $\sigma $ и $\zeta $ в ядре везде отрицательны и достигают значений –3 × 10^–5 с^–1.

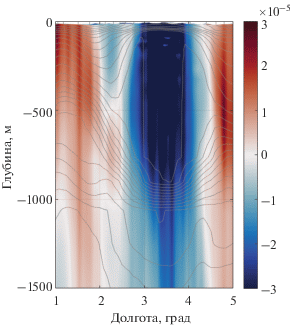
Потенциальная завихренность $\sigma $ характеризует вращение вихря и является динамической характеристикой. Размерность $\sigma $ отличается от размерности $PV$.

3.5. Объемная потенциальная завихренность

Для Лофотенского вихря в расчетах объемной потенциальной завихренности ${{\sigma }_{V}}$боковые границы вихря определялись по нулевым значениям $\zeta $ [46]. На рис. 6 представлены средние значения ${{\sigma }_{V}}$ в Лофотенском вихре на горизонтах. Видно, что в ядре вихря максимальные по модулю средние (по площади) значения ${{\sigma }_{V}}$ расположены в слое 200–800 м. Наибольшая отрицательная завихренность соответствует горизонту 500 м и составляет –1.3 × × 10^–5 с^–1. На горизонтах ниже 1000 м модуль осредненных значений ${{\sigma }_{V}}$ не превышает 1.0 × 10^–5 с^–1, а на горизонте 3000 м в два раза меньше и составляет 0.5 × 10^–5 с^–1.

Так как в поверхностном слое данных GLORYS1-2V1 содержится большое число выбросов, расчеты объемной потенциальной завихренности ${{\sigma }_{V}}$ производились от 16 м до дна (до 3000 м). Объемная потенциальная завихренность ${{\sigma }_{V}}$ для вихря объема V рассчитывалась по интегральной формуле:

Объемная потенциальная завихренность ${{\sigma }_{V}}$ для Лофотенского вихря равна –9.82 × 10⁶ с^–1. Для ядра (до 1000 м) объемная ${{\sigma }_{V}}$ составляет –2.28 × × 10⁸ с^–1.

Объемная потенциальная завихренность ${{\sigma }_{V}}$ характеризует мощность вихря.