1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 57, № 6, 2021

Известия РАН. Физика атмосферы и океана, 2021, T. 57, № 6, стр. 707-720

Некоторые особенности внутригодовой изменчивости потоков тепла в Северной Атлантике

К. П. Беляев a, b, c, В. Ю. Королев b, c, А. К. Горшенин c, *, А. И. Антипов b, М. А. Имеев b, Н. И. Кирюшкин b, М. А. Лобовский b

a Институт океанологии им. П.П. Ширшова Российской академии наук
117997 Москва, Нахимовский просп., 36, Россия

b Московский государственный университет имени М.В. Ломоносова
119991 Москва, Ленинские горы, 1, стр. 52, ГСП-1, Россия

c Федеральный исследовательский центр “Информатика и управление” Российской академии наук
119333 Москва, ул. Вавилова, 44, корп. 2, Россия

* E-mail: agorshenin@frccsc.ru

Поступила в редакцию 10.03.2021
После доработки 23.06.2021
Принята к публикации 11.08.2021

Полный текст (PDF)

Аннотация

В работе анализируются статистические закономерности внутригодовой изменчивости потоков тепла в Северной Атлантике при взаимодействии “океан–атмосфера”. В качестве математической модели изменчивости потоков тепла рассматривается диффузионный случайный процесс. Параметры этого процесса, то есть вектор сноса (дрифт) и матрица диффузии (или среднего квадратичного отклонения), оцениваются статистически с помощью оригинальных методов. По результатам данных реанализа ERA-5 за 2011–2020 гг. изучается поведение этих коэффициентов в Северной Атлантике и сопоставляется их поведение c поведением самих потоков тепла. Выделяются зоны максимума, минимума и среднего значения этих потоков по всей изучаемой области при суточном и шестичасовом осреднении, описывается их поведение и поведение их суточной изменчивости как случайных величин в течение года. Осуществляется статистическая подгонка параметрических моделей их распределений. Определяются области Северной Атлантики, в которых определяющее значение имеют систематические факторы (параметр сноса превышает параметр диффузии) и наоборот. Этот эффект обсуждается в терминах поведения параметров вероятностных распределений для инкрементов рассматриваемых процессов. Анализируется пространственно-временная изменчивость экстремальных характеристик потоков (максимума и минимума по расчетной области в фиксированный момент времени).

Ключевые слова: потоки тепла, океан–атмосфера, статистические модели, Северная Атлантика

ВВЕДЕНИЕ

Анализ потоков тепла в Северной Атлантике и его изменчивости – это одна из основных проблем современной метеорологии, океанологии и климатологии. На поверхности раздела атмосфера–океан турбулентные потоки тепла очень изменчивы на различных пространственно-временных масштабах и поэтому проблема их корректного описания требует особой аккуратности при постановке задачи. Разными авторами [1, 2] строились карты потоков в месячном осреднении, затем данные реанализа строились с суточным осреднением [3]. Также есть карты потоков, построенные за период с 1985 г. по настоящее время (2020 г.) [4] и также с суточным осреднением. Самые подробные карты реанализа при усвоении данных спутниковых наблюдений поверхностной температуры вариационными методами были построены с шестичасовым осреднением, в частности, в работах [5, 6].

Имея данные по потокам тепла, записанные в разных узлах сетки с заданными географическими координатами после реанализа, в литературе описаны различные методы их анализа. В работе [7] изучалась изменчивость потоков в районе тропических муссонов методами регрессионного анализа и скользящего среднего (ARIMA). В статье [8] потоки тепла в Атлантике изучались различными методами анализа временных рядов, в частности выделением трендов и гармонических составляющих, а в работе [9] строились распределения потоков в фиксированных точках сетки методами статистики, в частности подбирались оптимальные по методу максимального правдоподобия распределения и оценивались параметры этого распределения. Этим методом, в частности, заполнялись пропуски в рядах и (или) исправлялись ненадежно определенные значения потоков. Есть довольно значительный объем работ, в которых потоки тепла моделируются с помощью совместных моделей океан–атмосфера и сравниваются с наблюденными (пересчитанными) значениями реанализа в заданных точках. К этим работам можно отнести, например, статьи [10, 11].

Тем не менее, детальный и адекватный анализ и прогноз турбулентных потоков тепла маловероятен в ближайшем будущем. Дело тут не только и не столько в недостатке прямых измерений, сколько в сложности самого процесса взаимодействия между океаном и атмосферой. Поскольку сами потоки в точке или в ограниченной области связаны между собой и в целом представляют собой незамкнутую неравновесную термодинамическую систему, к ним не применимо представление о гауссовости соответствующих распределений и классические подходы термодинамики. Поэтому описание системы в целом, на больших пространственно-временных масштабах невозможно, слишком сложны внутренние процессы, описываемые неравновесными термодинамическими составляющими. Более перспективен, на наш взгляд, подход, при котором процессы взаимодействия разбиваются на отдельные блоки или под-процессы, и уже к ним применяются классические математические модели и методы.

В соответствии с этим подходом требуется “расчленить” процессы взаимодействия на такие под-процессы, описание которых позволило бы адекватно проанализировать, по возможности предсказать их поведение и уже потом из них сложить всю картину в целом. С другой стороны, рассматривать динамику турбулентных потоков тепла на очень мелком “атомарном” уровне тоже не особо продуктивно для определения глобальной, климатической изменчивости, так как процессы на очень мелком уровне не складываются обычным способом в глобальную динамику.

В настоящей работе турбулентные потоки тепла в точке представляются в виде диффузионного случайного процесса, с коэффициентами сноса и диффузии, зависящими как от точки, так и от рассматриваемого момента времени. Оригинальным методом, разработанным ранее в ряде работ авторов (см., например, статьи [12, 13]), эти коэффициенты статистически оцениваются по данным реанализа ERA-5. Ключевым предположением, используемым при оценивании этих параметров, является однородность случайного поля потоков, то есть считается, что изменение потоков за единицу времени зависит от значения потоков, а не от географической точки, где этот поток рассматривается. Это предположение вполне обоснованно, так как расчетные формулы потоков используют сами значения контактных сред, в нашем случае “вода–воздух”, а не их локацию. Поэтому при достаточно больших размерах рассматриваемой области для каждого интервала значений потоков тепла, от минимального до максимального значения потоков в фиксированную дату, найдется достаточно много пространственных точек и, соответственно, значений потоков, чтобы оценка вероятности (частоты) перехода значений потока из состояния $x$ в состояние $y$ за время $\Delta t$ была состоятельна. Детально этот метод изложен ниже

Цель данной статьи – получить и оценить внутригодовую изменчивость потоков тепла в точках одноградусной сетки, выделить особые зоны в рассматриваемой области, такие как зоны максимума, минимума и среднего потоков по области на каждый момент времени, и оценить их изменчивость, отдельно изучить вклад динамической и стохастической (турбулентной) составляющей в общую изменчивость потоков, локализовать и картировать их динамику. Кроме того, целью работы также является получение статистических характеристик коэффициентов сноса и диффузии, построенных по данным реанализа, анализ их пространственной и временной изменчивости в течении года, выделение сезонной и синоптической составляющей, а также связи этих характеристик, определяющих суточный и шестичасовой инкремент потоков тепла с самими потоками.

1. МЕТОД АНАЛИЗА И ДАННЫЕ НАБЛЮДЕНИЙ

Метод анализа

Основным математическим методом, используемым в работе, является представление процесса изменчивости потоков тепла в виде

(1)
$dX = a(t,X)dt + b(t,X)dW,$
где $X(t)$ − поток тепла в момент времени t, $dX = X(t + dt) - X(t)$ представляет собой изменчивость (инкремент) потока тепла за время dt = = t + dt – t в фиксированной точке, $a(t,X),b(t,X)$ − коэффициенты сноса и диффузии, зависящие от времени t и от значений процесса $X(t)$, $dW$− это стандартное обозначение гауссова белого шума с нулевым средним и единичной дисперсией, не зависящего от процесса $X(t)$. Представление (1) является обычным для описания случайных процессов диффузионного типа, в которых изменчивость самого процесса за малый промежуток времени $dt$ мала по сравнению с изменчивостью его среднего значения и дисперсии, и в котором эта изменчивость может рассматриваться как сумма квази-детерминированного процесса, определяемого сносом $a(t,X)$ (“квази” потому, что эта величина сама зависит от процесса X) и чисто случайного, независимого от первого слагаемого, определяемого диффузионной составляющей $b(t,X)dW$. Подробнее о диффузионных случайных процессах написано, например, в книге [14]. Далее, введем следующие величины: пусть условная вероятность $P(\left. y \right|x) = $ $P(X(t + dt) = \left. y \right|X(t) = x)$, если $y,x$ дискретны и, соответственно, условная плотность (производная Радона–Никодима) $p(\left. y \right|x)dx$ = = $p(X(t + dt)$ = $\left. y \right|x < X(t) = x + dx)$, если процесс $X(t)$ рассматривается как непрерывный. Чтобы отличать сам процесс $X(t)$ от его значений, последние будем обозначать маленькими буквами. Для определения коэффициентов $a(t,x),b(t,x)$ используются следующие формулы [14]

$\begin{gathered} a(t,x) = \underbrace {\lim }_{\Delta t \to 0}\frac{1}{{\Delta t}}\int\limits_t^{t + \Delta t} {(y - x} )p(\left. y \right|x)dy, \\ {{b}^{2}}(t,x) = \underbrace {\lim }_{\Delta t \to 0}\frac{1}{{\Delta t}}\int\limits_t^{t + \Delta t} {(y - x} {{)}^{2}}p(\left. y \right|x)dy. \\ \end{gathered} $

Таким образом, для определения коэффициентов $a(t,x),b(t,x)$ по формулам (2) достаточно знать условные вероятности $p(\left. y \right|x)$ при изменении процесса за два последовательных момента времени. В свою очередь для статистического определения этих вероятностей надо иметь выборку значений процесса $X(t)$ в каждой паре точек области и моменты $t$ и $t + dt$.

Ключевым предположением для статистического определения этих вероятностей является предположение об однородности случайного поля, в котором рассматривается процесс $X(t)$. А именно, предполагается, что распределения инкремента процесса $X(t)$, то есть вероятности перехода зависят только от значений этого процесса и не зависят непосредственно от той точки поля, где эти значения рассматриваются. Поэтому выборку значений процесса в точке можно заменить на выборку значений процесса по всей области, и, если это область достаточно обширна, такая выборка будет репрезентативна. Таким образом, оценки условных вероятностей по формуле (2) производятся следующим образом: на шаге $t$ все значения процесса $X(t)$ от ${{X}_{{\min }}}(t) = {{X}_{{\min }}}$ до ${{X}_{{\max }}}(t) = {{X}_{{\max }}}$ разбиваются на L интервалов, ${{X}_{i}} = {{X}_{{\min }}}$ + $i \times \frac{{{{X}_{{\max }}} - {{X}_{{\min }}}}}{L},$ $i = 0,L$ и фиксируются все точки области, где ${{X}_{i}} < X(t) = x < {{X}_{{i + 1}}}$. Пусть таких точек будет $n(x)$. На следующем шаге среди этих и только этих точек фиксируются все точки области, где $X(t + dt) = y$. Пусть таких точек будет m(y). Тогда в качестве оценки условной вероятности будет $\hat {P}(\left. y \right|x) = {{m(y)} \mathord{\left/ {\vphantom {{m(y)} {n(x)}}} \right. \kern-0em} {n(x)}}.$ Очевидно, что $0 \leqslant \hat {P}(\left. y \right|x)$ = ${{m(y)} \mathord{\left/ {\vphantom {{m(y)} {n(x)}}} \right. \kern-0em} {n(x)}} \leqslant 1$. Легко показать, что если $m(y),\,n(x) \to \infty $, то $\hat {P}(\left. y \right|x)$ → $P({y \mathord{\left/ {\vphantom {y x}} \right. \kern-0em} x})$, где $P(\left. y \right|x)$ – “истинная вероятность”, определяемая по заданной мере. Предложенный метод ранее подробно описан в статьях [12, 13]. Там же приведены доказательства состоятельности этих оценок.

Замечание. При практической реализации этого метода важно обеспечить, чтобы в каждом из интервалов $\left( {{{X}_{{\min }}} + i \times \frac{{{{X}_{{\max }}} - {{X}_{{\min }}}}}{L}} \right.,$ Xmin = (i + + 1)$\left. {\frac{{{{X}_{{\max }}} - {{X}_{{\min }}}}}{L}} \right),$ $i = 0,L - 1$ было хотя бы одно значение. При этом точность оценки вероятности $\hat {P}(\left. y \right|x)$ невозможно оценить без дополнительных предположений и условий. Однако можно отметить, что в дальнейшем потребуется не сама вероятность $\hat {P}(\left. y \right|x)$, а ее интегральные характеристики, коэффициенты $a(t,x),b(t,x)$, точность которых для практических применений не так важна.

Данные наблюдений

В работе использовались данные по потокам тепла, заданные в узлах одноградусной сетки с временным разрешением 6 ч с 1 января 2011 г. до 31 декабря 2020 г. Эти данные усреднялись на каждые сутки и в результате строился среднестатистический годовой ход за этот период (климатический годовой ход, как он определялся, например, в работе [15]). Потоки явного и скрытого тепла, соответственно, рассчитывались по формулам:

(3)
${{Q}_{h}} = {{c}_{p}}\rho {\text{ }}{{C}_{{\text{T}}}}{\text{ }}({{T}_{w}} - {{T}_{a}}){\text{ }}V,$
(4)
${{Q}_{e}} = L\rho {\text{ }}{{C}_{{\text{E}}}}{\text{ }}({{q}_{s}}--{\text{ }}q){\text{ }}V.$

То есть в формулах (3) и (4) потоки тепла явно рассчитываются через параметры на границе раздела океана и атмосферы – температуры воды, воздуха и модуля скорости ветра, ${{T}_{w}},\,\,{{T}_{a}},\,\,V$ соответственно, а также удельную влажность приводного воздуха q, максимальную для данной величины температуры поверхности океана насыщенную удельную влажность над поверхностью воды ${{q}_{s}}$. В качестве коэффициентов пропорциональности в соотношениях (3) и (4) служат коэффициенты обмена теплом CТ (число Шмидта) и влагой CE (число Дальтона) и удельная теплота испарения (L), удельная теплоемкость воздуха при постоянном давлении cp и его плотность ρ. В наших исследованиях значения потоков ${{Q}_{h}},{{Q}_{e}}$ считались уже известными, дополнительного расчета по формулам (3) и (4) не требовалось.

2. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ И АНАЛИЗ РЕЗУЛЬТАТОВ

Поведение потоков, его динамической и стохастической составляющих

В работе проводилось моделирование процессов изменчивости потоков тепла в Северной Атлантике и расчеты коэффициентов сноса и диффузии на каждый момент времени по формулам (2) с осреднением 6 и 24 ч. В статье приводятся только карты потока ${{Q}_{h}}$ на конец каждых двух месяцев, все значения также приводятся только для явного потока.

При воспроизведении рисунков для потоков, коэффициентов a и коэффициентов b весь интервал изменчивости соответствующих величин был поделен на 10 равных по вероятности попадания (частоте) под-интервалов. На рисунке это обозначено “0.1 ≥ qt”, “0.2 ≥ qt ≥ 0.1” и т.д. соответственно. Интервал изменчивости значений для явного потока изменялся в пределах от –470 до 90 вт/м2. Для коэффициентов $a\left( {t,\hat {x}\left( t \right)} \right)$ (обозначения приведены ниже) изменения были от –450 до 450 вт/(м2 сутки). Значения коэффициентов b $~\left( {t,\hat {x}\left( t \right)} \right)$ колебались от 0 до 230 (вт/м2 сутки)

Из рисунков видно, что направление движения потоков тепла осуществляется вдоль основных течений в Северной Атлантике в направлении юг–северо-восток в течении года (зима–лето–зима). Максимальные потоки зимой в Северной Атлантики (вдоль американского берега в зоне Гольфстрима и в море Баффина) перемещаются в течение года к северу и к северо-востоку в направлении Исландии, заметно усиливаясь к маю–августу и вновь ослабевая в период сентябрь–ноябрь. Зимой появляются заметные отрицательные потоки в центральных районах Северной Атлантики. Направление вращения потоков преимущественно против часовой стрелки (циклоническое) при положительном значении потока (то есть из океана в атмосферу). Зимой (ноябрь–март) появляются заметные отрицательные потоки (из атмосферы в океан), выраженные в основном в центральной части Северной Атлантики и имеющие преимущественно отрицательное вращение (по часовой стрелке). Средний по пространству поток положителен и варьируется в течение года от близкой к нулю величины (зимой) до примерно 50 вт/м2 в летний период. В летний период заметен также шторм-трек вдоль Гольфстрима–Северо-Атлантического течения, хорошо выделяемый на фоне положительных потоков в центральной и Северной Атлантике. В отдельных зонах, например, в море Баффина, поток почти всегда положителен, что понятно, там океан постоянно холодный в течение года, а атмосфера холоднее только в отдельные моменты в течении климатического года.

На рисунках разбиение на цветовые сегменты неравномерное, сделано в соответствии с эмпирическим распределением потоков на 10 квантилей, вверху в описании рисунков указана принятая цветовая шкала. Интервал изменчивости потоков приведен выше.

Внутригодовая изменчивость потоков тепла в Северной Атлантике достаточно хорошо изучена, и приведенные выше результаты в целом известны. Часть из них содержится, например, в вышеупомянутой статье [8]. Однако поведение инкремента потоков тепла и его изменчивость изучены гораздо меньше.

На рис. 2 показана изменчивость коэффициента сноса $a(t,\hat {x}(t))$, где в данном случае $\hat {x}(t)$ представляет собой географическую точку в расчетной области в момент времени t. То есть по формулам (2) вычислялось значение $a(t,x)$, где $x = X(t,\hat {x})$ − значение процесса $X(t,\hat {x})$ в точке области $\hat {x}(t)$ и в момент времени t. Приводятся шесть значений коэффициента $a(t,\hat {x}(t))$ на конец каждых 2 мес. аналогично рис. 1. Так же, как и для потоков, в приложении содержится двухминутное видео поведения этих коэффициентов на каждые сутки. Отметим существенные различия в поведении этой величины. В течение года эта величина в основном отрицательна и принимает минимальные значения до –450 вт/(м2 сутки). Положительные значения коэффициента сноса гораздо более локализованы, чем сами значения потока и преимущественно распространяются вдоль теплого течения Гольфстрим–Северо-Атлантическое течение в направлении юго-запад–северо-восток с циклоническим вращением (против часовой стрелки). Также заметные положительные значения этого коэффициента выражены в зимний период. Отрицательные значения этого коэффициента занимают гораздо большую акваторию, чем положительные значения, преимущественного направления перемещения не видно, направление вращения в основном антициклоническое (по часовой стрелке). Однако в пространстве области коэффициента $a(t,\hat {x}(t))$ структурированы, представляют собой связанные зоны, хаотических переходов практически нет. Интенсивность коэффициента сноса заметно возрастает в зимний период (октябрь–февраль) и снижается в летний. Цветовая шкала также выполнена в соответствии с эмпирическим распределением величины $a(t,\hat {x}(t))$ при разбиении на 10 квантилей. Значения потоков и квантилей указаны в описании рис. 2. Еще можно отметить, что интервал изменчивости коэффициента сноса оказывается больше интервала изменчивости самого явного потока.

Рис. 1.

Карты явных (Qh) потоков тепла в начале каждого 2-месячного периода в течение климатического года (1.01–1.11).

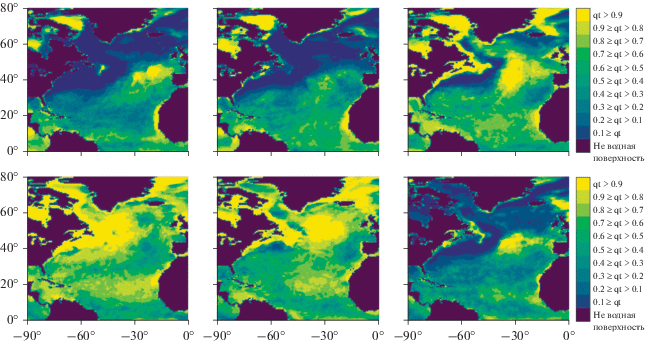
Рис. 2.

Поведение коэффициента сноса (главного компонента разности за одни сутки) потоков тепла Qh на конец каждого двухмесячного периода в течение года.

Поведение коэффициента диффузии $b(t,\hat {x}(t))$ достаточно хорошо прослеживает внутригодовой ход. Само поле коэффициента $b(t,\hat {x}(t))$ гораздо более хаотическое, чем поле потоков и поле коэффициента сноса. Это понятно, так как поле диффузии отражает именно хаотичность, нерегулярность процесса. В начале процесса (рис. 3) (январь–февраль) в крупном масштабе порядка 500–600 км поле этого коэффициента разделяет всю акваторию Северной Атлантики на две зоны – севернее и южнее линии раздела, проходящей примерно по южной границе крупномасштабных течений. Справа и южнее этой границы поле почти везде положительное, то есть диффузия присутствует в значительной мере, севернее наоборот – большое количество точек, где диффузия отсутствует, за исключением локальных областей размером отдельных синоптических вихрей. Однако в более мелком масштабе видны хаотические движения внутри ячеек, “иглообразная” структура изолиний, нарушение гладкости при поступательном движении юго-запад–северо-восток. Далее, начиная с апреля и до октября эта граница теряет структуру, превращается в несвязанные отдельные “островки” одинаковых значений, смещается к северу. Амплитуда этих значений заметно уменьшается и динамика юго-запад–северо-восток более не прослеживается, а появляется вертикальная линия в центральной части Атлантики. Преобладающего направления движения коэффициента $b(t,\hat {x}(t))$ в эти месяцы не наблюдается и сами значения становятся малыми. Затем динамика заметно интенсифицируется, и структура опять восстанавливается. И еще можно заметить, что близко к берегам значения диффузии всегда ненулевые, что тоже понятно, так как там сильны локальные неоднородности потоков.

Рис. 3.

Поведение диффузионного компонента инкремента потоков тепла Qh на конец двухмесячного периода в течение года.

Поскольку коэффициенты $a(t,\hat {x}(t))$ и $b(t,\hat {x}(t))$ имеют одинаковую размерность (вт/м2 сутки) и отражают соответственно динамическую и стохастическую составляющую в изменении (инкременте) потока, имеет смысл сравнить эти величины как по амплитуде, так и по фазе (то есть по величине и местоположению).

На рис. 4 приведены некоторые соотношения этих коэффициентов, причем по величине сравниваются только абсолютные значения, знак коэффициента $a(t,\hat {x}(t))$ не учитывается. Отмечаются также только области (отмеченные соответственно красным и белым), где коэффициент $a(t,\hat {x}(t))$ превосходит коэффициент $b(t,\hat {x}(t))$ и наоборот, величина этой разности не учитывается. Видно, что в целом по акватории преобладает стохастическая составляющая, что естественно, так как в поток между океаном и атмосферой – величина нерегулярная. Зона преобладания коэффициента $a(t,\hat {x}(t))$ (то есть зона, где $\left| {a(t,\hat {x}(t))} \right|$ −$b(t,\hat {x}(t))$ > 0) в основном располагается вдоль струйных течений (Гольфстрим–Северо-Атлантическое течение, Лабрадорское течение) и вдоль берегов, особенно в море Баффина, где сильны процессы обмена океан–материк.

Рис. 4.

Соотношение сноса/диффузии инкремента потока тепла в течение года на конец каждого двухмесячного периода.

В остальной части Северной Атлантики преобладает коэффициент $b(t,\hat {x}(t))$. В летний период область “красной зоны” заметно уменьшается, что естественно, к зиме возрастает. Есть незначительное изменение соотношения $\left| {{{a(t,\hat {x}(t))} \mathord{\left/ {\vphantom {{a(t,\hat {x}(t))} {(b(t,\hat {x}(t))}}} \right. \kern-0em} {(b(t,\hat {x}(t))}}} \right|$ в сезонной изменчивости (зимой до 1.5, летом до 1.2) (не показывается) в динамических районах, отмеченных выше.

Поведение максимума, минимума и среднего потоков

В этом разделе изучается поведение экстремальных характеристик потоков, построенных по данным по всей акватории в каждый момент времени. На рис. 5 приводятся графики распределений (гистограммы) максимума (зеленый цвет), минимума (синий цвет) и среднего потока, построенного по акватории суммарно за весь период времени с суточным осреднением, а на рис. 6 приводится временной ход этих величин за каждые сутки в течении климатического года. Анализ всех трех этих гистограмм показывает, что мы имеем дело с унимодальными распределениями, с ярко выраженными вершинами и неравномерно спадающими к нулю кривыми. Причем можно заметить, что поведение максимума и минимума в некотором смысле симметрично, спад к минимальным значениям для максимума почти повторяет спад к максимальным значениям для минимума и наоборот. По высоте эти две гистограммы также очень похожи. Обе эти гистограммы сильно отличаются от гауссовых, что подтверждает вывод о неравновесности или не замкнутости процессов формирования максимума и минимума потоков тепла. Гистограмма описывающая поведение среднего, по акватории потока в каждый момент времени занимает промежуточное положение, ее значения заметно меньше по высоте, и величина дисперсии, отражающая “толщину” этой гистограммы, также заметно меньше. Это свидетельствует о том факте, что величина среднего потока не показательна, его значения мало репрезентативны для оценки общей изменчивости потока в течение года. Гистограммы моделируются различными распределениями, на рис. 6 приводятся различные типы распределений, моделирующие эти гистограммы.

Рис. 5.

Гистограммы максимума, минимума и среднего значений потоков за весь период наблюдений.

Рис. 6.

Гистограммы аппроксимации минимума (а), среднего (б) и максимума (в) за весь период наблюдений.

Видно, что гистограмма, отвечающая максимальным значениям, в течение климатического года достаточно хорошо описывается духпараметрическим гамма-распределением с плотностью вероятностей $p(x) = \frac{{{{\beta }^{\alpha }}}}{{G(\alpha )}}{{x}^{{\alpha - 1}}}{{e}^{{ - \beta x}}}$, где $p(x)$ – плотность вероятности потока в точке $x$ (то есть плотность вероятности при значении потока, равного x), $\alpha ,\,\,\beta $ – параметры сдвига и масштаба соответственно (shape and scale parameters), $G(\alpha )$ – значения гамма-функции в точке $\alpha $. Такой же плотностью (только с другими параметрами) моделируется гистограмма минимума, а для среднего значения наилучшей аппроксимацией является кривая распределения Стьюдента, $p(x) = \frac{{G\left( {\frac{{n + 1}}{2}} \right)}}{{\sqrt {n\sigma \pi } G\left( {\frac{n}{2}} \right)}}$ ${{\left( {1 + \frac{{{{{(x - \mu )}}^{2}}}}{{{{\sigma }^{2}}n}}} \right)}^{{ - \frac{{n + 1}}{2}}}}$ с параметрами сдвига μ, масштаба σ и с n степенями свободы. Параметры полученных распределений указаны в описании рисунков. Однако подобные модели имеют чисто описательное значение, им практически невозможно дать разумное математическое обоснование, поскольку наблюдения не являются независимыми и однородными. В следующем параграфе будет показано, что с определенной степенью надежности можно утверждать, что независимыми (некоррелированными) и однородными можно считать приращения (инкременты) потоков, что позволяет дать некоторое математическое объяснение возникающим в такой ситуации моделям. Отметим, что в силу указанных обстоятельств в данной работе мы не проводим количественные оценки соответствия теоретического распределения данным наблюдений и не проводим тестов согласия, например, хи-квадрат теста.

Поведение временных рядов максимума, минимума и среднего значений

При анализе временной изменчивости максимума, минимума и средней величины потока, показанной соответственно на графиках рис. 7, можно заметить, что величины максимума и минимума достаточно сильно меняются в течение года, а среднее значение меняется заметно меньше, при этом все 3 величины в суточном осреднении (рис. 7) имеют заметный годовой ход, который можно смоделировать по формуле

(5)
${{X}^{l}}(t) = {{A}_{0}} + {{A}^{l}}\cos \omega t + {{B}^{l}}\sin \omega t + {{\xi }^{l}},$
где ${{X}^{l}}(t)$ – максимум, минимум или среднее значение процесса $X(t)$, l = 1, 2, 3 – соответственно, в момент времени t, ${{A}_{0}},{{A}^{l}},{{B}^{l}},\omega = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } T}} \right. \kern-0em} T}$ амплитуды и фазы годовой гармоники, Т = 1 год, ${{\xi }^{l}}$ стационарный в широком смысле случайный процесс.

Рис. 7.

Поведение максимума, минимума и среднего во времени в течении года. (а) – поток, (б) – инкремент потока с суточным осреднением.

Если рассматривать инкремент (то есть разность) при суточном осреднении, годовой ход выражен заметно меньше, среднее значение практически не меняется, но при этом поведение максимума и минимума имеет ярко выраженную симметрию, однако для инкремента можно отметить заметную “лохматость” графиков. Это связано с сильно выраженным суточным ходом потоков в низких широтах и, как следствие, к “размыванию значений максимума и минимума в течение суток в пространстве. Количественные оценки разброса значений в суточном осреднении максимума от ‒400 вт/м2 до почти 100 вт/м2 заметно превосходят разброс значений максимумов для инкремента, где минимальный поток составляет 50 вт/м2 при примерно таком же значении максимума. Минимальные значения потока по абсолютной величине в суточном осреднении такие же, как и для максимума, то есть около 100 вт/м2, а в максимуме меньше, около 90 вт/м2.

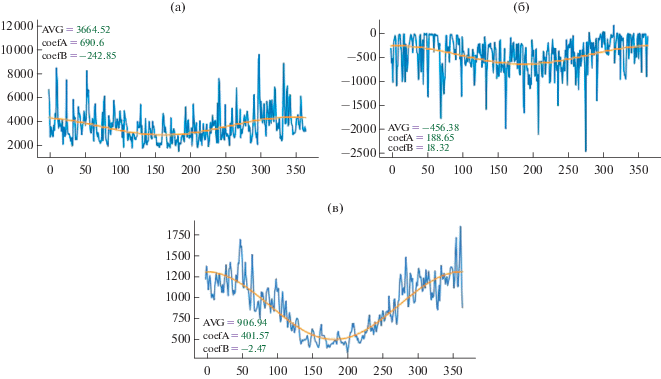
На осредненных графиках (рис. 7) годовой ход не слишком выражен, он однако присутствует в потоках тепла в конкретные годы. Поэтому на графиках рис. 8 и 10 приведены оценки годовых гармоник, полученных за один конкретный год. На графиках на рис. 8 показаны величины AVG = A0, и амплитуды Аг, Вг – соответствующие годовой гармонике.

Рис. 8.

Моделирование максимума (а), минимума (б) и среднего (в) в виде суммы гармоники годового хода и случайного остатка.

Стохастическое дифференциальное уравнение (1) по сути описывает поведение приращений процесса. Для более детального изучения статистических закономерностей поведения изменчивости потоков тепла исходные данные были преобразованы: во-первых, был исключен длительный тренд (годовой ход) и, во-вторых, были взяты приращения исходного временного ряда. Такое преобразование позволяет рассматривать получившиеся значения как однородную статистическую выборку некоррелированных наблюдений. После выделения и отделения сезонного хода, то есть вычитания оцененной функции ${{X}^{l}}(t) = {{A}_{0}} + {{A}^{l}}\cos \omega t$ + ${{B}^{l}}\sin \omega t$, где $\omega = \frac{{2\pi }}{Т}$, Т равен году (в соответствующих единицах временной сетки), для приращений остатка ${{\xi }^{l}}$ также были построены гистограммы, по которым были подогнаны параметрические распределения вероятностей. Наилучшее согласие с гистограммами инкремента потоков в каждой точке рассматриваемой области Северной Атлантики продемонстрировало распределение Стьюдента со сдвигом. На рис. 9 для каждой точки Северной Атлантики показаны значения параметров сдвига, масштаба и оценено количество степеней свободы распределения Стьюдента, задаваемого плотностью вероятностей вида

$\begin{gathered} p(x) = \frac{{G\left( {\frac{{n + 1}}{2}} \right)}}{{\sqrt {n\sigma \pi } G\left( {\frac{n}{2}} \right)}}{{\left( {1 + \frac{{{{{(x - \mu )}}^{2}}}}{{{{\sigma }^{2}}n}}} \right)}^{{ - \frac{{n + 1}}{2}}}}, \\ - \infty < x < \infty . \\ \end{gathered} $
Рис. 9.

Пространственные распределения параметров нецентрального распределения Стьюдента, (а) – параметр сдвига, (б) – параметр диффузии, (в) – число степеней свободы.

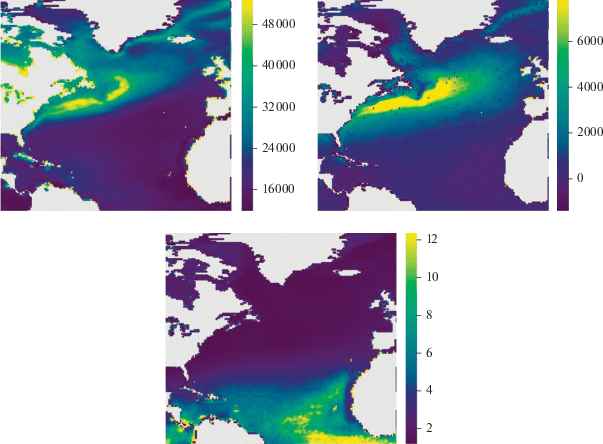
Из этих рисунков хорошо видно, что области больших значений параметров масштаба (диффузии) σ и больших по модулю (но отрицательных) значений параметра сдвига μ, рис. 9а, в основном совпадают с зоной Гольфстрима, с направлением убывания юг–север. Расположение обеих областей практически совпадает, но можно заметить, что область максимальных значений параметра масштаба σ лежит вдоль берегов, находясь немного севернее области максимальных по модулю (но отрицательных) значений параметра локации (сдвига) μ. При этом параметр формы n распределения Стьюдента (“число степеней свободы”) может принимать нецелые значения и в основном лежит в пределах 2 ± 1.

На рис. 10а–10в построены распределения инкрементов максимума, минимума и среднего после отделения годовой гармоники, показанной на рис. 8.

Рис. 10.

Аппроксимация распределений случайного остатка от максимума (а), минимума (б) и среднего (в) после отделения годового хода.

Как видно из этих рисунков, распределения как минимумов, так и максимумов достаточно хорошо аппроксимируются сразу несколькими теоретическими кривыми с достаточной степенью точности. В этом нет ничего удивительного, все теоретические распределения похожи, разница между ними проявляется только в области малых вероятностей (“хвостов), а этих значений мало.

Интересно проанализировать величины $a(t,{{\hat {x}}^{l}}(t)),$ $({{b}^{l}}(t,{{\hat {x}}^{l}}(t))$, l = 1, 2, 3, взятых соответственно в т. максимума и минимума. На рис. 11а, 11б приведены временные графики поведения величины $a(t,{{\hat {x}}^{l}}(t))$ для минимума и максимума, соответственно, в суточном осреднении. Видно, что коэффициент $a(t,{{\hat {x}}^{l}}(t))$ для минимума имеет выраженный годовой ход, с практически постоянными значениями летом и максимальными разбросами зимой, что отражает малую изменчивость значения минимума потока летом и максимальную в зимний период. Для максимума это не так, этот коэффициент достаточно хаотичен в течение всего года, но отрицателен, что понятно, так как показывает временную производную максимума, то есть изменение в минус.

Рис. 11.

Временное поведение величины $a(t,{{\hat {x}}^{l}}(t))$ при значении ${{\hat {x}}^{l}}(t)$: (а) – минимума, (б) – максимума в суточном осреднении.

Изменчивость характеристики $(b(t,\hat {x}(t))$ в суточном осреднении в течение климатического года мала, близка к нулю и поэтому не приводится. Поведение этих характеристик гораздо менее информативно. Дисперсия для максимума менее вариабельна, чем для минимума, в противовес тому факту, что изменение самого максимума более динамично, чем изменение минимума. Какой-либо периодичности в этой изменчивости не видно, что не противоречит тому факту, что основная крупно- и среднемасштабная изменчивость содержится в коэффициенте сноса. Поэтому представление процесса по формуле (5) оправдано.

ЗАКЛЮЧЕНИЕ И ВЫВОДЫ

В работе использован ранее разработанный авторами оригинальный метод на основе теории случайных процессов, обобщающий классическое разложение временных рядов на регулярные и стохастические составляющие. С его помощью изучается поведение потоков тепла в Северной Атлантике и анализируется их внутригодовая изменчивость. Выделяются структурные кластеры потоков, в частности их максимумы, минимумы и средние значения по всей рассматриваемой области, показывается, что для этих кластеров можно выделить их регулярные и стохастические составляющие их изменчивости, а также описать их распределения на внутригодовом масштабе. Выделяются области, в которых доминирует та или иная составляющая изменчивости, описывается их пространственно-временная динамика. Также показано, что временной ход максимума, минимума и среднего значений по области имеет ярко выраженную годовую гармонику при суточном осреднении данных наблюдений, а в шестичасовом осреднении эти гармоники не выражены, а наоборот, большее влияние оказывают случайные характеристики.

При анализе временного хода максимума и минимума также показано, что при разложении этих величин по предложенной схеме поведение динамической составляющей заметно сильнее стохастической компоненты и имеет соответствующий знак, а именно: минус в случае максимума и плюс в случае минимума, что подтверждает корректность предложенной схемы анализа. Хорошее согласие распределения Стьюдента, имеющего довольно тяжелые хвосты (убывающие степенным образом), может быть объяснено тем, что оно является (масштабной) смесью нормальных (гауссовых) распределений при смешивающем обратном гамма-распределении.

Такие распределения возникают в качестве асимптотических для процессов типа неоднородных случайных блужданий, в частности, обобщенных дважды стохастических пуассоновских процессов [16]. Эти процессы описывают поведение случайных блужданий, случайные скачки которых имеют конечные вторые моменты (дисперсии), причем точки скачков образуют пуассоновский процесс со случайной интенсивностью. Как показано в [16], такие процессы являются наилучшими моделями неоднородных хаотических потоков событий. Подобные модели распределения приращений данных хорошо согласуются с моделью (1), в которой коэффициенты могут считаться случайными и зависящими как от самого процесса, так и от факторов, внешних по отношению к рассматриваемому процессу. Более того, информация о том, что смешивающее распределение является обратным гамма, может быть использована для конкретизации зависимости коэффициентов модели (1) от соответствующих факторов, что представляет собой отдельную задачу и определяет одно из направлений дальнейших исследований.

В статье использованы данные за последнее десятилетие (2011–2020 гг.). В силу наблюдаемых на подобных временных интервалах изменений климата, такой выбор представляется значительно более перспективным, по сравнению с анализом значений за конкретный год. Предложенный метод может использоваться и для расчета вероятностных распределений изучаемых величин и их статистического анализа и прогноза с использованием известных численных схем анализа вероятностных процессов, в частности численных решений уравнений Фоккера−Планка−Колмогорова. Также в качестве направления дальнейших исследований можно упомянуть применение метода скользящего разделения смесей вероятностных распределений [17–19] для оценивания временной эволюции распределений коэффициентов стохастических дифференциальных уравнений, описывающих анализируемые процессы [20].

Список литературы

  1. Josey S., Kent E.C., Taylor P.K. New insights into the ocean heat budget closure problem from analysis of the SOC air-sea flux climatology // J. Climate. 1999. V. 12. P. 2856–2880.

  2. Grist J.R., Josey S.A. Inverse Analysis Adjustment of the SOC Air–Sea Flux Climatology Using Ocean Heat Transport Constraints // J. Climate. 2003. V. 16. P. 3274–3295.

  3. Berry D.I., Kent E.C. A new air-sea interaction gridded dataset from ICOADS with uncertainty estimates // Bulletin of the American Meteorological Society. 2009. V. 90. Iss. 5. P. 645–656.

  4. Yu L., Weller R.A. Objectively analyzed air–sea heat fluxes for the global ice-free oceans (1981–2005) // Bull. Am. Meteorol. Soc. 2007. V. 88. P. 527–539.

  5. Grodsky S., Bentamy A.A., Carton J.A., Pinker R.T. Intraseasonal latent heat flux based on satellite observations // J. Climate. 2009. V. 22. Iss. 17. P. 4539–4556.

  6. Andersson A., Klepp C., Fennig K., Bakan S., Grasl H., Schulz J. Evaluation of HOAPS-3 ocean surface freshwater flux components // J. Applied Meteorology and Climatology. 2011. V. 50. Iss. 2. P. 379–398.

  7. Kumar M., Kumar A., Mahanti N.C., Mallik C., Shukla R.K. Surface flux modelling using ARIMA technique in humid subtropical monsoon area // J. Atmospheric and Solar-Terrestrial Physics. 2009. V. 71. Iss. 12. P. 1293–1298.

  8. Gulev S.K., Latif M., Keenlyside N., Park W., Koltermann K.P. North atlantic ocean control on surface heat flux on multidecadal timescales // Nature. 2013. V. 499. Iss. 7459. P. 464–467.

  9. Gulev S.K., Belyaev K.P. Probability distribution characteristics for surface air-sea turbulent heat fluxes over the global ocean // J. Climate. 2012. V. 25. P. 184–206.

  10. Yu L., Weller R.A., Sun B. Improving latent and sensible heat flux estimates for the Atlnatic Ocean (1988–99) by a synthesis approach // J. Climate. 2004. V. 17. P. 373–393.

  11. Kirtman B.P., Stockdale T., Burgman R. The ocean’s role in modeling and predicting seasonal-to-interannual climate variations // International Geophysics. 2013. V. 103. P. 625–643.

  12. Belyaev K.P., Tanajura C.A.S., O’Brien J.J. A data assimilation method used with an ocean circulation model and its application to the tropical Atlantic // Applied Mathematical Modelling. 2001. V. 25. Iss. 8. P. 655–670.

  13. Tanajura C.A.S., Belyaev K.P. On the oceanic impact of a data assimilation method in a coupled ocean-land-atmosphere-model // Ocean Dynamics. 2002. V. 52. P. 123–13

  14. Гихман И.И., Скороход А.В. Введение в теорию случайных процессов. М.: Наука, 1976.

  15. Зверяев И.И., Яшаяев И.М. Сезонная изменчивость нолей давления, температуры воды и воздуха в Северной Атлантике по данным COADS // Изв. РАН. Физика атмосферы и океана. 1996. № 2. С. 222–239.

  16. Королев В.Ю. Вероятностно-статистические методы декомпозиции волатильности хаотических процессов. М.: Издательство Московского университета, 2011. 512 с.

  17. Королев В.Ю., Горшенин А.К., Гулев С.К., Беляев К.П. Статистическое моделирование турбулентных потоков тепла между океаном и атмосферой с помощью метода скользящего разделения конечных нормальных смесей // Информатика и ее применения. 2015. Т. 9. Вып. 4. С. 3–13.

  18. Korolev V.Yu., Gorshenin A.K., Gulev S.K., Belyaev K.P. Statistical modeling of air-sea turbulent heat fluxes by finite mixtures of Gaussian distributions // Communications in Computer and Information Science. 2015. V. 564. P. 152–162.

  19. Gorshenin A., Korolev V., Kuzmin V., Zeifman A. Coordinate-wise versions of the grid method for the analysis of intensities of non-stationary information flows by moving separation of mixtures of gamma-distribution // Proceedings of 27th European Conference on Modelling and Simulation, 2013. Dudweiler, Germany: Digitaldruck Pirrot GmbH. P. 565–568.

  20. Горшенин А.К., Королев В.Ю., Щербинина А.А. Статистическое оценивание распределений случайных коэффициентов стохастического дифференциального уравнения Ланжевена // Информатика и ее применения. 2020. Т. 14. Вып. 3. С. 3–12.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал