1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 58, № 4, 2022

Известия РАН. Физика атмосферы и океана, 2022, T. 58, № 4, стр. 467-471

Внутренние гравитационные волны в океане при обтекании подводного препятствия сдвиговым течением

В. В. Булатов a, *, И. Ю. Владимиров b, **

a Институт проблем механики им. А.Ю. Ишлинского РАН
119526 Москва, просп. Вернадского, 101-1, Россия

b Институт океанологии им. П.П. Ширшова РАН
119997 Москва, Нахимовский просп., 36, Россия

* E-mail: internalwave@mail.ru
** E-mail: iyuvladimirov@rambler.ru

Поступила в редакцию 10.03.2022
После доработки 27.03.2022
Принята к публикации 11.04.2022

Полный текст (PDF)

Аннотация

В работе рассмотрена задача о генерации внутренних гравитационных волн, возникающих при набегании стратифицированного потока со сдвиговым течением на одиночное подводное препятствие. Предполагается, что частота плавучести постоянна, сдвиговое течение линейное и одномерное. Получены интегральные представления решения при выполнении условия устойчивости Майлса-Ховарда. Аналитически построены решения краевой спектральной задач, которые выражаются через функции Бесселя мнимого индекса. Приведены результаты численных расчетов дисперсионных кривых и фазовых картин возбуждаемых волновых полей. Численно изучена трансформация фазовых картин полей внутренних гравитационных волн в зависимости от параметров генерации.

Ключевые слова: стратифицированная среда, внутренние гравитационные волны, частота плавучести, сдвиговые течения, спектральная задача, дисперсионные зависимости, фазовые картины

В реальных природных стратифицированных средах (океан, атмосфера) генерация и распространение внутренних гравитационных волн (ВГВ) в значительной степени связаны с вертикальной и горизонтальной динамикой фоновых сдвиговых течений [1–4]. В океане такие течения могут проявляться, например, в области сезонного термоклина и оказывать заметное влияние на эволюцию ВГВ [5–7]. В общей постановке описание динамики ВГВ в стратифицированной среде с фоновыми полями сдвиговых течений является весьма сложной задачей уже в линейном приближении [1, 2, 8, 9]. В этом случае задача сводится к анализу системы уравнений в частных производных, и при одновременном учете вертикальной и горизонтальной неоднородности эта система уравнений не допускает разделение переменных [2, 10–15]. Для исследования механизма взаимовлияния течений и ВГВ можно рассматривать различные модельные представления частоты плавучести и сдвиговых течений [8, 9, 16–18]. Одним из заметных механизмов возбуждения ВГВ в океане можно рассматривать, например, генерацию волн фоновым течением на склонах поперечных хребтов в проливах [3–7]. Поэтому целью настоящей работы является построение решений, описывающих генерацию ВГВ стратифицированным сдвиговым потоком, набегающим на подводное препятствие.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается вертикально стратифицированная среда конечной глубины $H$ с фоновым сдвиговым течением, набегающим на одиночное подводное препятствие. Профиль дна описывается функцией $z = - H + h(x,y),$ $h(x,y) \ll H$. Сдвиговое течение вдоль оси $Ox$ – одномерное и линейное: $U(z) = {{U}_{0}}$ + $({{U}_{0}} - {{U}_{H}})z{\text{/}}H$, U0 = U(0) > 0, UH = = U(–H) > 0. Тогда в линейном приближении и приближении Буссинеска вертикальная компонента скорости $W$удовлетворяет уравнению [9, 18]

(1)
$\begin{gathered} \mathop U\nolimits^2 (z)\frac{{{{\partial }^{2}}}}{{\partial x{}^{2}}}\left( {\Delta + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right)W + {{N}^{2}}(z)\Delta W = 0, \\ \Delta = \frac{{{{\partial }^{2}}}}{{\partial x{}^{2}}} + \frac{{{{\partial }^{2}}}}{{\partial y{}^{2}}},\,\,\,\,{{N}^{2}}(z) = - \frac{g}{{{{\rho }_{0}}(z)}}\frac{{d{{\rho }_{0}}(z)}}{{dz}}, \\ \end{gathered} $
где ${{N}^{2}}(z)$ – квадрат частоты Брента-Вяйсяля (частоты плавучести), которая далее предполагается постоянной $N(z) = N = {\text{const}}$, $g$ – ускорение свободного падения, ${{\rho }_{0}}(z)$ – невозмущенная плотность среды. Также выполнено условие устойчивости Майлса-Ховарда для числа Ричардсона [19–22]: $Ri = {{N}^{2}}{{\left( {\frac{{dU}}{{dz}}} \right)}^{{ - 2}}} > 1{\text{/}}4$.

Граничное условие на поверхности

(2)
$W = 0\,\,{\text{при}}\,\,z = 0.$

Линеаризованное граничное условие на дне [8, 9]

(3)
$W = U( - H)\frac{{\partial h(x,y)}}{{\partial x}}\,\,{\text{при}}\,\,z = - H.$

В безразмерных переменных $x* = {{\pi x} \mathord{\left/ {\vphantom {{\pi x} H}} \right. \kern-0em} H},$ y* = = ${{\pi y} \mathord{\left/ {\vphantom {{\pi y} H}} \right. \kern-0em} H},$ $z* = {{\pi z} \mathord{\left/ {\vphantom {{\pi z} H}} \right. \kern-0em} H},$ $W* = {{\pi W} \mathord{\left/ {\vphantom {{\pi W} {NH}}} \right. \kern-0em} {NH}},$ $t* = tN$, $M(z*)$ = $\pi U{{(z*)} \mathord{\left/ {\vphantom {{(z*)} {NH}}} \right. \kern-0em} {NH}}$ = $a + bz*,$ $a = {{\pi {{U}_{0}}} \mathord{\left/ {\vphantom {{\pi {{U}_{0}}} {NH}}} \right. \kern-0em} {NH}},$ b = = ${{\pi ({{U}_{0}} - {{U}_{H}})} \mathord{\left/ {\vphantom {{\pi ({{U}_{0}} - {{U}_{H}})} {N{{H}^{2}}}}} \right. \kern-0em} {N{{H}^{2}}}}$, (индекс “*” далее опускается) задача (1)–(3) имеет вид

(4)
$\begin{gathered} {{M}^{2}}(z)\frac{{{{\partial }^{2}}}}{{\partial x{}^{2}}}\left( {\Delta + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right)W + \Delta W = 0, \\ W = 0~\,\,{\text{при}}\,\,z = 0, \\ W = M( - \pi )\frac{{\partial h(x,y)}}{{\partial x}}\,\,{\text{при}}\,\,z = - \pi . \\ \end{gathered} $

2. ИНТЕГРАЛЬНЫЕ ФОРМЫ РЕШЕНИЯ И ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Решение задачи (4) ищется в виде

(5)
$\begin{gathered} W(x,y,z,) = \frac{1}{{4{{\pi }^{2}}}} \times \\ \times \,\,\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\varphi (\mu ,\nu ,z)\exp ( - i(\mu x + \nu y - \omega t))d\nu d\mu } } , \\ \end{gathered} $
где функция $\varphi (\mu ,\nu ,z)$ определяется из решения краевой задачи

(6)
$\frac{{{{\partial }^{2}}\varphi }}{{\partial {{z}^{2}}}} + {{k}^{2}}(1 - {{(\mu M(z))}^{2}})\varphi = 0,$
(7)
$\begin{gathered} \varphi = 0\,\,{\text{при}}\,\,z = 0,\,\,\,\,\varphi = - iA(\mu ,\nu )\,\,{\text{при}}\,\,z = - \pi , \\ A(\mu ,\nu ) = \mu M( - \pi )h{\kern 1pt} *(\mu ,\nu ),\,\,\,\,{{k}^{2}} = {{\mu }^{2}} + {{\nu }^{2}}, \\ h{\kern 1pt} *(\mu ,\nu ) = \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {h(x,y)\exp (i(\mu x + \nu y))dxdy} } . \\ \end{gathered} $

Построим решение краевой задачи (6)–(7). Два линейно независимых решения уравнения (6) с нулевыми граничными условиями выражаются через модифицированные функции Бесселя мнимого индекса ${{I}_{{ \pm i\lambda }}}:$ ${{f}_{ \pm }}(z,\mu ,\nu )$ = $\sqrt {2\alpha \mu M(z)} {{I}_{{ \pm i\lambda }}}(\alpha \mu M(z)),$ $\lambda = \sqrt {{{\alpha }^{2}} - 1{\text{/}}4,} $ $\alpha = {k \mathord{\left/ {\vphantom {k {b\mu }}} \right. \kern-0em} {b\mu }},$ где функции ${{f}_{ \pm }}(z,\mu ,\nu )$ – комплексно сопряжены [9, 18]. Действительное решение, удовлетворяющее граничному условию на поверхности $z = 0$, имеет вид: $\Phi (z,\mu ,\nu )$ = = $i({{f}_{ + }}(z,\mu ,\nu ){{f}_{ - }}(0,\mu ,\nu )$ – ${{f}_{ - }}(z,\mu ,\nu ){{f}_{ + }}(0,\mu ,\nu )),$ или $\Phi (z,\mu ,\nu )$ = $ - \operatorname{Im} ({{f}_{ + }}(z,\mu ,\nu ){{f}_{ - }}(0,\mu ,\nu )).$

Тогда решение краевой задачи (6)–(7) имеет вид

$\varphi (z,\mu ,\nu ) = - iA(\mu ,\nu )\frac{{\Phi (z,\mu ,\nu )}}{{\Phi ( - \pi ,\mu ,\nu )}}.$

Проведем в (5) интегрирование по переменное $\mu $. Для этого контур интегрирования необходимо сместить на комплексной плоскости $\mu $ вверх на малое расстояние $\varepsilon > 0$. Это необходимо для того, чтобы удовлетворить условию излучения, то есть отсутствию волн вверх по потоку. Тогда при $x \to - \infty $ интеграл (5) по экспоненциально мал. При $x \to \infty $ контур интегрирования по переменной $\mu $ необходимо перевести в нижнюю полуплоскость. Основной вклад в интеграл будут давать полюса функции $\varphi (z,\mu ,\nu )$, то есть нули функции $\Phi ( - \pi ,\mu ,\nu )$. Эти нули – собственные числа задачи (6) с нулевыми граничными условиями., или дисперсионные кривые $\mu = \pm {{\mu }_{n}}(\nu )$. Тогда, учитывая вычеты в полюсах $\mu = \pm {{\mu }_{n}}(\nu )$, решение можно представить в виде суммы мод

(8)
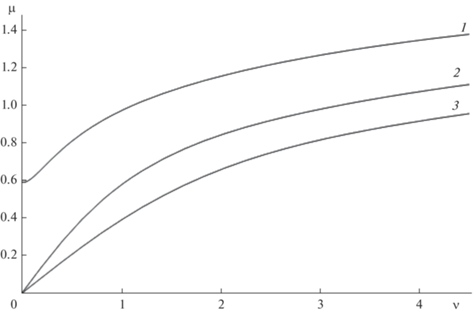
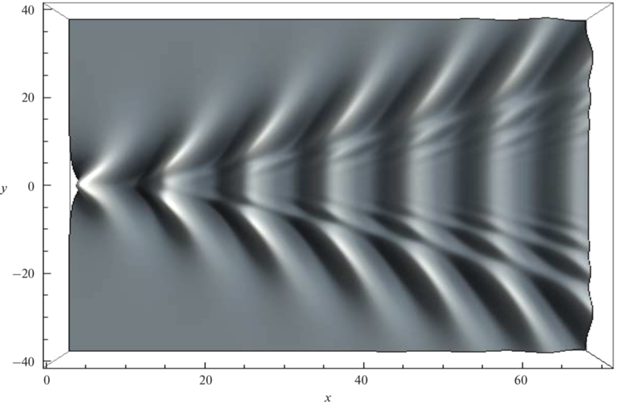
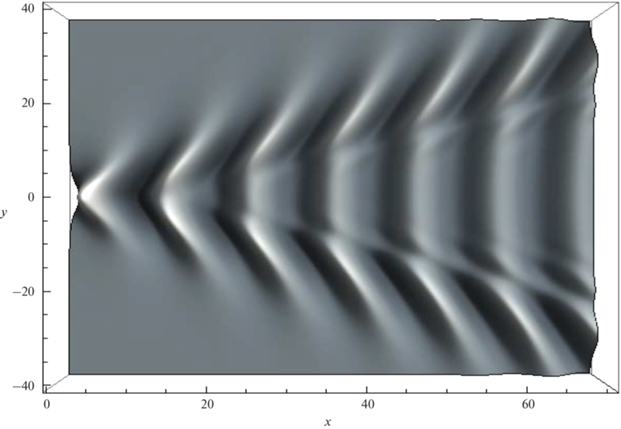
$\begin{gathered} W = \sum\limits_{n = 1}^\infty {{{W}_{n}}} ,{{W}_{n}} = \\ = - \frac{2}{\pi }\int\limits_0^\infty {A({{\mu }_{n}}(\nu ),\nu ){{B}_{n}}\cos ({{\mu }_{n}}(\nu )x)\cos (\nu y)d\nu } , \\ {{B}_{n}} = {{\Phi }_{n}}(z,{{\mu }_{n}}(\nu ),\nu ){\text{/}}\frac{{\partial {{\Phi }_{n}}(z,{{\mu }_{n}}(\nu ),\nu )}}{{\partial \mu }}, \\ \end{gathered} $
где ${{\Phi }_{n}}(z,{{\mu }_{n}}(\nu ),\nu )$ – собственная функция задачи (5) с нулевыми граничными условиями. Дисперсионные кривые рассчитываются численно или асимптотически, используя дебаевские асимптотики или приближения Вентцеля – Крамерса – Бриллюэна для модифицированной функции Бесселя ${{I}_{{ \pm i\lambda }}}(\lambda )$ при больших значениях параметра $\lambda $ [9, 18]. Асимптотический анализ интегралов (8) может быть проведен с помощью метода стационарной фазы (неравномерная асимптотика) или метода эталонных интегралов (равномерная асимптотика). Равномерная асимптотика интегралов (8) выражается через функцию Эйри и ее производную [8, 9].

Численные расчеты проводились с использованием вычислительной системы “Математика”. Значения параметров, величины которых в размерных единицах характерны для условий реального океана были следующие: $a = 1.35,$ $b = 0.27,$ $Ri = 13.7$. Параметр $b$ есть величина обратная квадратному корню из числа Ричардсона: $b = 1{\text{/}}\sqrt {Ri} $. Параметр $a > 1$ определяет отношение амплитуды приповерхностного течения ${{U}_{0}}$ к максимальной групповой скорости распространения ВГВ в океане, равной $NH{\text{/}}\pi $, что наблюдаемо в условиях реального океана [3, 4]. На рис. 1 приведены результаты расчетов дисперсионных кривых первых трех мод ${{\mu }_{n}}(\nu ),n = 1,2,3$. Отметим, что только у первой моды значение в нуле положительно (${{\mu }_{1}}(0) > 0$), остальные моды ${{\mu }_{n}}(0) = 0,\,\,\,\,n > 1$. Профиль дна описывается гладкой функцией $h(x,y) = 0.05\pi $$\exp ( - {{\beta }^{2}}{{x}^{2}} - {{\gamma }^{2}}{{y}^{2}})$, значение $z = - 1$. На рис. 2 приведены результаты расчетов функции ${{W}_{1}}$ при $\beta = 0.1,\,\,\,\,\gamma = 1.0$, обтекаемое препятствие имеет большую протяженность вдоль набегающего течения. На рис. 3 приведены результаты расчетов функции ${{W}_{1}}$ при $\beta = 1.0,\,\,\,\,\gamma = 0.1$, обтекаемое препятствие имеет большую протяженность поперек набегающего течения. Таким образом, полученные численные результаты показывают, что на фазовую структуру волнового поля вниз по потоку влияют не только параметры течения, но также геометрия обтекаемого препятствия, степень его пространственной асимметрии и угол набегания стратифицированного потока.

Рис. 1.

Дисперсионные кривые ${{\mu }_{n}}(\nu ),n = 1,2,3$: линия 1 – первая мода, линия 2 – вторая мода, линия 3 – третья мода.

Рис. 2.

Первая мода вертикальной скорости.

Рис. 3.

Первая мода вертикальной скорости.

3. ЗАКЛЮЧЕНИЕ

В работе решена задача о генерации полей внутренних гравитационных волн, возбуждаемых при обтекании стратифицированного потока с фоновым сдвиговым течением одиночного подводного препятствия. В предположении постоянства частоты плавучести и модельного линейного распределения сдвигового течения построено аналитическое решение спектральной задачи, которое выражается через функцию Бесселя мнимого индекса. Численно исследованы дисперсионные соотношения и фазовые картины возбуждаемых волновых полей для различных режимов волновой генерации, характерных для реальных условий океана. Показано, что учет формы обтекаемого препятствия, а также угла набегания сдвигового течения может являться причиной заметной пространственной трансформации возбуждаемых вниз по потоку волновых полей. Полученные результаты дают возможность эффективно рассчитывать фазовую структуру волновых полей, а также исследовать различные режимы волновой генерации для модельных представлений частоты плавучести и сдвиговых течений, в том числе генерацию волновых полей возвышениями океанического дна сложной геометрии.

Работа выполнена по темам государственного задания: В.В. Булатов (№ АААА-А20-120011690131-7), И.Ю. Владимиров (№ FMWE-2021-0002) и частичной финансовой поддержке РФФИ проект № 20-01-00111А.

Список литературы

  1. Fabrikant A.L., Stepanyants Yu.A. Propagation of waves in shear flows. World Scientific Publishing, 1998. 304 p.

  2. Miropol’skii Yu.Z., Shishkina O.V. Dynamics of internal gravity waves in the ocean. Kluwer Academic Publishers, Boston, 2001. 406 p.

  3. Morozov E.G. Oceanic internal tides. Observations, analysis and modeling. Berlin: Springer, 2018. 317 p.

  4. Velarde M.G., Tarakanov R.Yu., Marchenko A.V. (Eds.). The ocean in motion. Springer Oceanography. Springer International Publishing AG, 2018. 625 p.

  5. Morozov E.G., Tarakanov R.Yu., Frey D.I., Demidova T.A., Makarenko N.I. Bottom water flows in the tropical fractures of the Northern Mid-Atlantic Ridge // J. Oceanography. 2018. V. 74(2). P. 147–167.

  6. Frey D.I., Novigatsky A.N., Kravchishina M.D., Morozov E.G. Water structure and currents in the Bear Island Trough in July-August 2017 // Russ. J. Earth Sciences. 2017. V. 17. ES3003.

  7. Khimchenko E.E., Frey D.I., Morozov E.G. Tidal internal waves in the Bransfield Strait, Antarctica // Russ. J. Earth. Science. 2020. V. 20. ES2006.

  8. Булатов В.В., Владимиров Ю.В. Волны в стратифицированных средах. М.: Наука, 2015. 735 с.

  9. Булатов В.В. Новые задачи математического моделирования волновой динамики стратифицированных сред. М.: Издательство “ОнтоПринт”, 2021. 277 с.

  10. Young W.R., Phines P., Garret C.J.R. Shear flows dispersion, internal waves and horizontal mixing // J. Phys. Oceanography, 1982. V. 12(6). P. 515–527.

  11. Bouruet-Aubertot P.I., Thorpe S.A. Numerical experiments of internal gravity waves an accelerating shear flow // Dyn. Atm. Oceans. 1999. V. 29. P. 41–63.

  12. Meunier P., Dizиs S., Redekopp L., Spedding G. Internal waves generated by a stratified wake: experiment and theory // J. Fluid Mech., 2018. V. 846. P. 752–788.

  13. Fraternale F., Domenicale L, Staffilan G., Tordella D. Internal waves in sheared flows: lower bound of the vorticity growth and propagation discontinuities in the parameter space // Phys. Rev. 2018.V. 97. № 6. P. 063102.

  14. Slepyshev A.A., Vorotnikov D.I. Generation of vertical fine structure by internal waves in a shear flows // Open J. Fluid Mechanics, 2019. V. 9. P. 140–157.

  15. Howland C.J., Taylor J.R., Caulfield C.P. Shear-induces breaking of internal gravity waves // J. Fluid Mechanics. 2021. V. 921. A24.

  16. Булатов В.В., Владимиров Ю.В., Владимиров И.Ю. Внутренние гравитационные волны от осциллирующего источника возмущений в океане // Изв. РАН. ФАО. 2021. Т. 57. № 3. С. 362–373.

  17. Булатов В.В., Владимиров И.Ю. Амплитудно-фазовая структура полей внутренних гравитационных волн в океане со сдвиговыми течениями // Изв. РАН. ФАО. 2022. Т. 58. № 2. С. 233–235.

  18. Bulatov V.V., Vladimirov Yu.V. Dynamics of internal gravity waves in the ocean with shear flows // Russ. J. Earth Sciences. 2020. V. 20. ES4004.

  19. Miles J.W. On the stability of heterogeneous shear flow // J. Fluid Mech. 1961. V. 10 (4). P. 495–509.

  20. Hirota M., Morrison P.J. Stability boundaries and sufficient stability conditions for stably stratified, monotonic shear flows // Physics Letters A. 2016. 380(21). P. 1856–1860.

  21. Churilov S. On the stability analysis of sharply stratified shear flows // Ocean Dynamics. 2018. 68. P. 867–884.

  22. Gavrileva A.A., Gubarev Yu.G., Lebedev M.P. The Miles theorem and the first boundary value problem for the Taylor–Goldstein equation // J. Applied and Industrial Mathematics. 2019. 13(3). P. 460–471.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал